Сети и графы
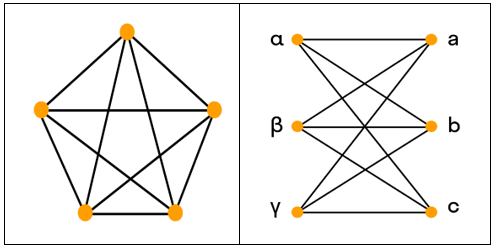
На практике часто необходимо при заданных условиях и ограниченных ресурсах для построения сети выбирать из потенциально возможных структур лучшую в некотором смысле, например, устойчивую к неисправностям (отказам) связей между узлами (каналов) транспортной сети, сети связи, сетей нефте- и газопроводных и многих других. Предлагается рассматривать ряд задач поиска оптимального решения в рамках числовых примеров. Актуальность проблемы несомненна, даже наше городское жилье охвачено большим числом обеспечивающих удобства и комфорт сетями различного назначения: электрическими, снабжения холодной и горячей водой, газопроводной, теплоснабжения, телевизионной, радиотрансляционной, интернетом, канализацией, мусоропроводом, охранного видеонаблюдения и др.














