О линейной регрессии: байесовский подход к курсу рубля
9 min
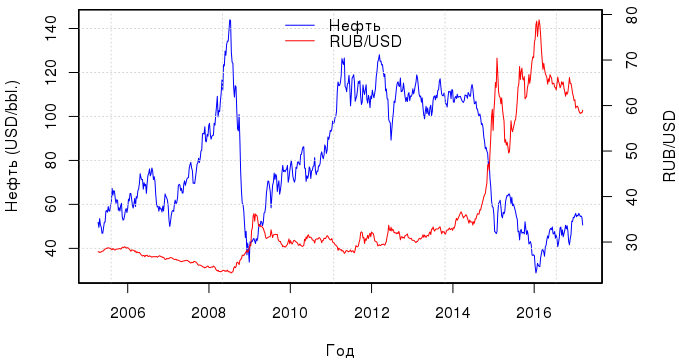
Не секрет, что курс рубля напрямую зависит от стоимости нефти (и от кое-чего еще). Этот факт позволяет строить довольно интересные модели. В своей статье о линейной регрессии я коснулся некоторых вопросов, посвященных диагностике модели, а за кадром остался такой вопрос: есть ли более эффективная, но не слишком сложная альтернатива линейной регрессии? Традиционно используемый метод наименьших квадратов прост и понятен, но есть и другие подходы (не такие понятные).

 Сначала я хотел честно и подробно написать о методах снижения размерности данных —
Сначала я хотел честно и подробно написать о методах снижения размерности данных — 
 Недавно мне принесли ноутбук — очень хороший ноутбук — по меркам 2004 года, конечно (за такой в то время можно было и убить
Недавно мне принесли ноутбук — очень хороший ноутбук — по меркам 2004 года, конечно (за такой в то время можно было и убить  ). И со знакомой многим мантрой «тыжпрограммист*ля» попросили разобраться, почему столько лет стабильно работавшее устройство вдруг отказалось загружаться. А я, в общем-то, не электронщик, и даже не совсем программист — так, с R/Matlab/Python балуюсь. Но знакомые были очень хорошие, и пришлось таки взять ноут.
). И со знакомой многим мантрой «тыжпрограммист*ля» попросили разобраться, почему столько лет стабильно работавшее устройство вдруг отказалось загружаться. А я, в общем-то, не электронщик, и даже не совсем программист — так, с R/Matlab/Python балуюсь. Но знакомые были очень хорошие, и пришлось таки взять ноут.  Иногда так бывает: задачу можно решить чуть ли не арифметически, а на ум прежде всего приходят всякие интегралы Лебега и функции Бесселя. Вот начинаешь обучать нейронную сеть, потом добавляешь еще парочку скрытых слоев, экспериментируешь с количеством нейронов, функциями активации, потом вспоминаешь о SVM и Random Forest и начинаешь все сначала. И все же, несмотря на прямо таки изобилие занимательных статистических методов обучения,
Иногда так бывает: задачу можно решить чуть ли не арифметически, а на ум прежде всего приходят всякие интегралы Лебега и функции Бесселя. Вот начинаешь обучать нейронную сеть, потом добавляешь еще парочку скрытых слоев, экспериментируешь с количеством нейронов, функциями активации, потом вспоминаешь о SVM и Random Forest и начинаешь все сначала. И все же, несмотря на прямо таки изобилие занимательных статистических методов обучения,  Иногда возникает необходимость ускорить вычисления, причем желательно сразу в разы. При этом приходится отказываться от удобных, но медленных инструментов и прибегать к чему-то более низкоуровневому и быстрому. R имеет довольно развитые возможности для работы с динамическими бибиотеками, написанными на С/С++, Fortran или даже Java. Я по привычке предпочитаю С/С++.
Иногда возникает необходимость ускорить вычисления, причем желательно сразу в разы. При этом приходится отказываться от удобных, но медленных инструментов и прибегать к чему-то более низкоуровневому и быстрому. R имеет довольно развитые возможности для работы с динамическими бибиотеками, написанными на С/С++, Fortran или даже Java. Я по привычке предпочитаю С/С++. Однажды для презентации мне понадобились анимированные графики. С графиками, собственно, проблем не возникло, а для их анимации пришлось воспользоваться еще одним пакетом
Однажды для презентации мне понадобились анимированные графики. С графиками, собственно, проблем не возникло, а для их анимации пришлось воспользоваться еще одним пакетом  Довольно часто встречаются неполные наборы данных, в которых некоторые переменные не определены. В языке R содержимое таких переменных задается как «Not Available» — или сокращенно NA. Соответственно, возникает вопрос, как поступать с неопределенными значениям: стоит ли их игнорировать или откорректировать каким-либо образом?
Довольно часто встречаются неполные наборы данных, в которых некоторые переменные не определены. В языке R содержимое таких переменных задается как «Not Available» — или сокращенно NA. Соответственно, возникает вопрос, как поступать с неопределенными значениям: стоит ли их игнорировать или откорректировать каким-либо образом?  Эта статья посвящена
Эта статья посвящена