Постановка задачи
Есть двигатель постоянного тока. Задача — разработать, собрать и протестировать устройство, позволяющиее реализовать контур тока применительно к этому двигателю. Желаемое время переходного процесса на застопоренном двигателе (без противо-ЭДС) — не более 10мс. Интерфес связи с внешним управляющим контроллером — SPI.
Двигатель постоянного тока, коллекторный, максимальное напряжение 24В, рабочий ток до 5А.
Что значит — контур тока? Самые распространённые драйверы для управления двигателями это всякие вариации полумостов, которые усиливают напряжение. А мне хочется, чтобы драйвер брал на вход не напряжение, а силу тока. Сила, развиваемая электроприводом, прямо пропорциональна силе протекающего тока. А значит, и прямо пропорциональна ускорению на валу двигателя. Такой контур тока позволит избежать извращений, на которые нужно идти без него, как я это делал тут.
Я разбил этот текст на две статьи:
- 1. Измерение сопротивления и индуктивности двигателя
- 2. Разработка управляющего контура
Вот так выглядит макет управляющего железа:

Железо
В состав системы будут входить:
- Силовая микросхема ключей, принимающая входной PWM сигнал и усиливающая его.
- Датчик тока.
- Управляющий микроконтроллер, реализующий обратную связь и закон управления.
Силовой драйвер
В качестве силового драйвера выбрана широкодоступная плата ($18) от Pololu на базе микросхемы Freescale MC33926, максимальная частота ШИМ 20кГц, 5А в пике, коммутируемое напряжение от 5 до 28 вольт.
Этот чип был взят за его возможность измерения абсолютной величины протекающего тока, которая в итоге не была использована. Таким образом, можно немного сэкономить, взяв более дешёвый драйвер со схожими характеристиками.
Датчик тока и его проверка
В качестве датчка тока выбран датчик Холла Allegro ACS714 ($3), выдающий аналоговый сигнал с центром в 2.5В и 185мВ/А, типичная ошибка 1.5%. На датчик была добавлена RC-цепочка в качестве фильтра низких частот с частотой среза 16кГц.
Датчик тока был запитан от 4.96В источника, последовательно с датчиком был подключен резистор, через который было пропущено 2А. Теоретическое напряжение на выходном пине должно быть 4.96/2 + (2 * 0.185 +- 1.5%), измерение показало 2.84 В, что укладывается в расчётные параметры. Затем было поменяно направление течения тока через резистор, при -2А измеренное напряжение на выходном пине датчика составило 2.11В, что опять укладывается в расчётные параметры:

Эта проверка была необходима, т.к. я купил несколько макеток с ACS712 и ACS714 от разных производителей, и в параметры даташита попал только один!
Микроконтроллер
В качестве управляющего микроконтроллера выбран ATMega328p, работающий на частоте 16МГц. Обвязка микроконтроллера — китайский клон Arduino Nano v3 ($1.5).
Микроконтроллер генерирует ШИМ сигнал через восьмибитный счётчик с делителем 8, таким образом, частота ШИМ сигнала 16 * 10^6 /255 /8 = 7.8 кГц, что укладывается в максимально доступные для драйвера 20кГц.
Делитель АЦП микроконтроллера установлен на 128; поскольку каждое измерение требует примерно 13 тактов, максимальная частота измерений протекающего тока равна примерно 16 * 10^6 / 128 / 13 = 9.6 кГц. Измерения производятся в фоновом режиме, извещая основную программу об окончании при помощи вызова соответствующего прерывания.
Логи
Я долго бился над тем, как записывать происходящее внтри микроконтроллера, ведь памяти у него совсем немного. В итоге я обнаружил, что родной SPI интерфейс очень быстрый, и в итоге вся отладочная информация передаётся микроконтроллером по интерфейсу SPI, для её записи был применён широкодоступный ($10 на дилэкстриме, $6 на алиэкспрессе) китайский клон логического анализатора Saelae Pro 8 Logic. После совсем нетрудных манипуляций по перепрошивке VID/PID, он может быть использован с родным софтом от Saelae. Я пользуюсь sigrok (pulseview). У него исключительно простой формат лог-файлов, которые я просто читаю своей самописной программкой в пятьдесят строк. Я купил этот анализатор по совету gbg, который мне дистанционно чинил мой спектрум (спасибо тебе огромное!), и считаю это самым выгодным вложением денег за последние два года.
Например, я подал синусоидальный сигнал (в ШИМ) на выход контроллера, и логический анализатор его прекрасно видит:

Всё это было соединено вместе, фотография дана в заголовке поста.
Лирическое отступление
Практически все статьи, что я размещаю здесь, являются моим рабочим дневником. Я чему-то учусь (в данном случае теории управления) и старательно записываю то, что узнал. Лучший способ записать — это написать объяснение того, как это всё работает. Затем статьи выкладываю на разных площадках, например тут.
Целей при написании текста у меня две:
а) получить обратную связь от людей, которые знают больше меня. Например, практически всё, что я узнал для данных двух статей, мне рассказал уважаемый Arastas, прошу любить и жаловать: человек, который тратит личное время на обучение таких оболтусов, как я.
Опять же, gbg, который написал мне линейную алгебру для моих лекций по компьютерной графике, а потом за много тысяч километров по телефону дебажил мне электронику.
б) просто записать: таким образом я получаю библиотеку личного опыта, к которой периодически возвращаюсь. Кстати, тематические медиа, какой процент авторов соглашаются на ваши условия программы поддержки?
Необходимый ликбез
Преобразование Фурье
Первое, что нужно понять, читая мои тексты: я считаю, что функция и вектор — это одно и то же. Все разговоры про бесконечности на меня навевают скуку и заслоняют суть происходящего. Обобщённые функции и тому подобное — это способ рассмотреть патологические случаи используя тот же самый язык, что и случаи, где никаких патологий нет. Вот только патологии меня не интересуют.
На эту тему хорошо высказался Валерий Иванович Опойцев (Босс):
В любой области полезно оказаться в подходящей среде устного общения, где осыпается книжная шелуха. Там иногда ничего не меняется по сути, зато возникает чувство попадания в колею и освобождения от догм. Для науки, которая всегда в маске, это особенно важно. Суть за кадром, перед глазами — кружева. И вечно чего-то не хватает. То простоты, то сложности, да точно и не определишь — чего. Что-то куда-то шагает, ты — на обочине, а время уходит в песок, не говоря о жизни.
Далее предпринимается попытка сдвинуть ситуацию с места, моделируя письменную среду, где «спадают покровы». Внешняя канва содержания более-менее неясна из оглавления, но главная цель — та, что за кадром. Снять вуаль, грим, убрать декорации. Переупростить, даже приврать слегка, ибо дозирование правды — краеугольный камень объяснения. Результаты, перегруженные деталями, не пролезают куда надо. Озарение случается, когда пухнущая голова проваливается на уровень «дважды два», в то время как счет идет на миллионы. Такая уж тут диалектика.
Если у нас есть вектор (7,12,18,-2), то его можно рассматривать как набор коэффициентов во взвешенной сумме. 7*(1,0,0,0) + 12*(0,1,0,0) + 18*(0,0,1,0) + (-2)*(0,0,0,1). Ровно так же можно считать этот вектор значениями функции в точках 0, 1, 2, 3, ведь наши векторы (0,1,0,0) и ему подобные можно рассматривать как сдвиг единичного импульса:

Если постоянно увеличивать количество векторов (сдвинутых единичных импуьсов) в базисе, то получим обычные функции.
К сожалению, с таким базисом бывает довольно неудобно работать. Давайте рассмотрим следующую функцию в качестве примера:
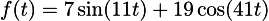
Мы уже беседовали о том, что такое преобразование Фурье. Если кратко, то это смена базиса.
В нашем случае преобразование Фурье — это функция из вещественных чисел в комплексные:
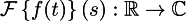
Аргумент функции (вещественное число) — это просто номер базисной функции или вектора (на самом деле, пары базисных функций), а её значение — это соответствующая (пара) координат в для этих двух векторов в базисе. Базис Фурье — это синусы и косинусы различных частот. Частота и является номером базисной функции.
Для нашей конкретной функции f(t), которая уже являетя взвешенной суммой синуса и косинуса, очень легко посчитать её разложение в базис Фурье:

То есть, наша функция f(t) имеет нулевые координаты для всех векторов базиса, кроме векторов номер 11 и 41.
Чем полезен базис Фурье? Например тем, что операция дифференцирования линейно преобразует этот базис. Допустим, мы хотим посчитать преобразование Фурье от производной f'(t). Как это сделать? Как вариант, в лоб: сначала посчитать производную, а затем посчитать преобразование Фурье:

Очевидно, что при дифференцировании sin(x) он станет sin(x+90°), то есть крайне легко найти соответствие разложение в базис Фурье исходной функции и её производной:
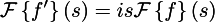
Умножение на i — это просто поворот комплексной плоскости, который соответствует +90° в аргументе нашей функции. То есть, операция дифференцирования, которую сложно делать в базисе единичных импульсов, в базисе Фурье — это просто масштабирование и поворот на 90 градусов. Красиво, правда?
Преобразование Лапласа
Примерно та же самая история происходит и с преобразованием Лапласа. К сожалению, в отличие от базиса Фурье, базис Лапласа неортогонален, поэтому для интуитивного понимания чуточку более сложен. Ну да не суть. Лаплас пошёл немного дальше. Если у Фурье в базисе были только синусоиды, то у Лапласа в базисе синусоиды с экспоненциальным затуханием. Откуда он их взял? Это крайне, крайне полезно при решении линейных дифференциальных уравнений. Давайте подумаем, какая функция преобразуется сама в себя при дифференцировании? Экспонента. А при дифференцировании два раза? Синус. А их комбинации дают все возможные функции, которые могут появиться при решении (линейных) диффуров, что и использовал маркиз дё Лаплас.
Не будем вдаваться в подробности того, как выводятся эти свойства (лучше рассмотрите внимательно свойства базиса Фурье, он проще), давайте просто отметим следующие факты:
1. Преобразование Лапласа линейно:

2. Преобразование Лапласа производной — это аффинное действие над преобразованием самой функции:
3.

Переходим непосредственно к делу
Итак, если у нас есть двигатель постоянного тока, то протекающий ток I(t) и напряжение на клеммах U(t) связаны следующим дифференциальным уравнением, где w(t) — это скорость вращения вала двигателя:

Здесь L — это индуктивность, а R — сопротивление, которые мы и ищем. Я не буду повторять, откуда вылезает этот диффур, так как уже подробно и на пальцах его расписывал (см. «уравнения Максвелла на пальцах»).
Поскольку наша задача найти L и R, давайте жёстко зафиксируем вал двигателя, таким образом заставив w(t) быть нулевой:

По совету Arastas я подал два типа сигналов на мой двигатель: меандр и синусоиду. Затем я измерил протекающий ток, картинка получается примерно следующая:

Здесь синие кривые — это входное напряжение, котороя я контролирую, а зелёные — это измерения силы тока, полученные при помощи ACS714.
Мой микроконтроллерный код, который генерирует 11 экспериментов с меандром и синусоидами различных амплитуд и частот, можно посмотреть здесь.
Давайте решим наше дифференциальное уравнение для обоих типов сигнала напряжения, получим параметрический выходной сигнал силы тока, и подберём параметры, чтобы теоретическая кривая как можно лучше аппроксимировала реальные измерения.
Входной сигнал — функция Хэвисайда (полупериод меандра)
Итак, w(t) = 0, начальные условия I(0) = 0, ток в самом начале не течёт. Приложим постоянное напряжение U0 к клеммам мотора, как себя должен будет вести протекающий ток?
Давайте возьмём преобразование Лапласа от левой и правой частей дифференциального уравнения (1):
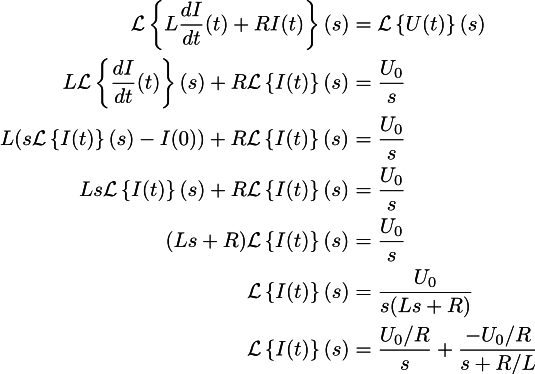
Для получения второй строчки я использовал линейность преобразования Лапласа, U0/s — взял из таблицы (обычно преобразования Лапласа вручную не считают, пользуются таблицами).
Для получения третьей строки использовано свойство производной.
Последняя строчка получается из предпоследней использованием метода неопределённых декомпозиций. Смысл этого перехода в том, чтобы опять получить табличную функцию. Разумеется, в двадцать первом веке руками это считать ни к чему.
Теперь осталось применить обратное преобразование Лапласа (для правой части мы смотрим таблицу) и мы решили наш диффур. Переход в базис Лапласа превратил дифференциальное уравнение в обычное алгебраическое!

Быстрая проверка результата: по истечении нескольких миллисекунд индуктивность уже не будет играть роли, и мы получим протекающий ток U_0 / R (закон Ома). В самом же начале протекающий ток равен нулю и экспоненциально возрастает, причём скорость возрастания напрямую зависит от индуктивности. Sanity check passed.
Файл с измерениями лежит здесь. Три колонки, секунды, приложенное напряжение (в вольтах), измеренная сила тока (в амперах).
Вот код, который подбирает параметры сопротивления и индуктивности для этого эксперимента:
Скрытый текст
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
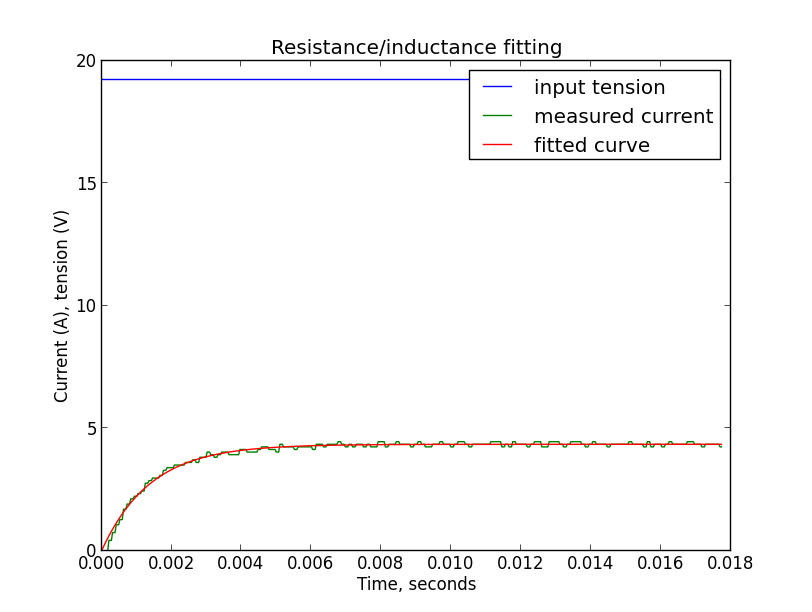
U0 = 19.2
def unit_step_current(x, R, L):
return [U0/R - U0/R*np.exp(-t*R/L) for t in x]
data = np.genfromtxt('unit_step_19.2V.csv', delimiter=',', names=['t', 'V', 'A'])
[R, L] = curve_fit(unit_step_current, data['t'], data['A'])[0]
print(R, L)
fig = plt.figure()
ax1 = fig.add_subplot(1,1,1)
ax1.set_title("Resistance/inductance fitting")
ax1.set_xlabel('Time, seconds')
ax1.set_ylabel('Current (A), tension (V)')
ax1.plot(data['t'], data['V'], color='b', label='input tension')
ax1.plot(data['t'], data['A'], color='g', label='measured current')
model=unit_step_current(data['t'], R, L)
ax1.plot(data['t'], model, color='r', label='fitted curve')
ax1.legend()
plt.show()
Он говорит, что хорошо подходит пара R=4.4 Ома, L=6мГенри, вот график:
Входной сигнал — синус
Повторим процедуру для синусоиды напряжения с амплитудой U0 и частотой F0. Применим преобразование Лапласа к уравнению (1), сначала к правой части:
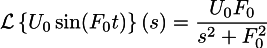
а потом и к левой:
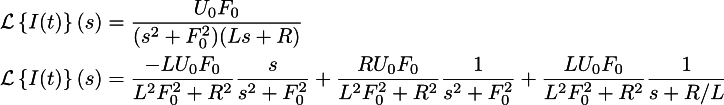
Теперь обратное преобразование нам даст следующий закон протекания тока:
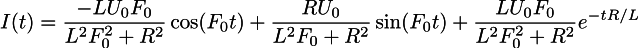
Опять быстрый sanity check: нулевой ток в самом начале, несколько миллисекунд переходных процессов (экспонента, напрямую зависящая от индуктивности). По истечению некоторого времени протекающий ток — это взвешенная сумма синуса и косинуса одной и той же частоты (частота равна входной, это хорошо). Эта сумма даёт синусоиду, чуть сдвинутую во времени. Отлично, результат правдоподобен.
Измерения лежат здесь, а код подбора параметров тут. Он даёт примерно такие же значения сопротивления и индуктивности, что нам и требовалось. Вот график:

Заключение
Почему не измерить параметры напрямую, зачем весь этот огород с микроконтроллерами? Во-первых, мне нечем измерять индуктивность. Да и измерение сопротивления двигателя омметром может иметь свои нюансы.
Далее, параметры, найденные при высокой амплитуде сигнала, не совсем совпадают с тем, что получается при низких напряжениях. Может быть интересно (тут не рассмотрено) делать модель не только двигателя, а всей системы в целом, включая нелинейность ШИМ-драйвера.
Ну а дальше осталось разработать регулятор, который будет на вход брать необходимую силу тока. Оставайтесь на связи!