
Введение
Часто, для обеспечения большой дальности полета, к самолету снаружи подвешивают дополнительные баки. Подвесные баки бывают сбрасываемые и не сбрасываемые.
Сбрасываемые подвесные баки после расходования из них топлива сбрасываются так же, как и авиационные бомбы с замков бомбодержателей, на которые они подвешиваются.
Питание из подвесных баков осуществляется включением трубопроводов от этих баков в общую систему питания двигателя топливом через запорный или многоходовой кран.
Интересным фактом является то, что во вьетнамских джунглях после войны стали находить много сброшенных американскими самолётами топливных баков.
Крестьяне распиливают баки вдоль и получаются две лодки. Такая лодка не ржавеет, мало весит, а благодаря аэродинамической форме на ней очень легко грести.

Неплохо было бы иметь такую лодку, но при этом, не очень хочется, чтобы самолёты с подвесными баками над нами летали.
Аэродинамическое сопротивление (АС) подвесного топливного бака
В зависимости от режима полёта и формы бака, будут преобладать те или иные компоненты аэродинамического сопротивления. Например, для затуплённых тел вращения, движущихся с большой сверхзвуковой скоростью, сопротивление имеет волновой характер.
Для хорошо обтекаемых тел, движущихся с небольшой скоростью, преобладает сопротивление трения и потери на вихреобразование.
Разрежение, возникающее на задней торцевой поверхности обтекаемого тела, также приводит к возникновению результирующей силы, направленной противоположно скорости тела.
Аэродинамическое сопротивление Fa характеризуют безразмерным аэродинамическим коэффициентом сопротивления Cx:

где ρ — плотность невозмущённой среды, v — скорость движения тела относительно этой среды, S— характерная площадь тела, Cx— безразмерный коэффициент аэродинамического сопротивления, обычно определяют экспериментально, а для простых форм вращения и расчётом.
Компоновка подвесного топливного бака из тел вращения по критерию минимума площади S и коэффициента Cx
Воспользуемся данными по расчету коэффициента лобового сопротивления (Cx) простых тел и сравнением полученного результата с экспериментом приведенными в публикации [1]:

Для тел вращения, расположенных на концах бака с цилиндром между ними (для удержания основной массы топлива), объёмом
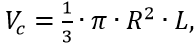 площадью поверхности
площадью поверхности  можно выбрать такие варианты компоновки:
можно выбрать такие варианты компоновки:конус (при H=R) –объём
 площадь поверхности
площадь поверхности 
конус (при H<>R)–объём
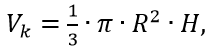 площадь поверхности
площадь поверхности 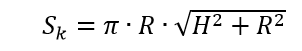
полусфера –объём
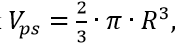 площадь поверхности
площадь поверхности 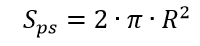


Зададимся объёмом бака в 3 м3: Vb=Vps+Vc+Vk, Vb=3, определим размеры для оптимальной компоновки из следующего листинга, когда условие для минимума Cx (2h=d или H=R) не выполняются:
# -*- coding: utf8 -*-
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
def objective(x):# целевая функция - площадь поверхности бака
x1=x[0]# искомый радиус R цилиндра и основания конуса
x2=x[1]# искомая высота H конуса, когда условие H=R не выполняется
x3=x[2]# искомая длина L цилиндра
return 2*np.pi*x1**2+2*np.pi*x1*x3+np.pi*x1*((x1**2)+(x2**2))**0.5
def constraint(x): # ограничение на объём бака
return (2/3)*np.pi*(x[0]**3)+np.pi*x[2]*(x[0]**2)+(1/3)*x[1]*np.pi*(x[0]**2)-3
x0=[1,1,1]# начальные значения для поиска локального минимума
b=(0.0,1)# ограничение по не отрицательным значениям переменных
bnds=(b,b,b)
con={'type': 'ineq','fun':constraint}
res = minimize(objective, x0,bounds=bnds,constraints=con)
e=round(res['fun'],3)
e1=round(res['x'][0],3)
e2=round(res['x'][1],3)
e3=round(res['x'][2],3)
print ("Расчётное значение площади подвесного бака :%s"%e)
print ("Расчётное значение радиуса подвесного бака :%s"%e1)
print ("Расчётное значение высоты конуса подвесного бака :%s"%e2)
print ("Расчётное значение длины цилиндра подвесного бака :%s"%e3)
Получим:
Расчётное значение площади подвесного бака :10.253
Расчётное значение радиуса подвесного бака :0.878
Расчётное значение высоты конуса подвесного бака :0.785
Расчётное значение длины цилиндра подвесного бака :0.393
При заданном объёме бака Vb=3, определим размеры для оптимальной компоновки из следующего листинга, когда условие для минимума Cx (2h=d или H=R) выполняются :
# -*- coding: utf8 -*-
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
def objective(x):# целевая функция - площадь поверхности бака
x1=x[0] # искомый радиус R цилиндра и основания конуса, высота которого H=R
x2=x[1]# искомая длина L цилиндра
return 2*np.pi*x1**2+2*np.pi*x1*x2+np.pi*x1*(2*(x1**2))**0.5
def constraint(x): # ограничение на объём бака
return (2/3)*np.pi*(x[0]**3)+np.pi*x[1]*(x[0]**2)+(1/3)*x[0]*np.pi*(x[0]**2)-3
x0=[1,1]# начальные значения для поиска локального минимума
b=(0.0,1)# ограничение по не отрицательным значениям переменных
bnds=(b,b)
con={'type': 'ineq','fun':constraint}
res = minimize(objective, x0,bounds=bnds,constraints=con)
e=round(res['fun'],3)
e1=round(res['x'][0],3)
e2=round(res['x'][1],3)
print ("Расчётное значение площади подвесного бака :%s"%e)
print ("Расчётное значение радиуса подвесного бака :%s"%e1)
print ("Расчётное значение высоты конуса подвесного бака :%s"%e1)
print ("Расчётное значение длины цилиндра подвесного бака :%s"%e2)Получим:
Расчётное значение площади подвесного бака :10.259
Расчётное значение радиуса подвесного бака :0.877
Расчётное значение высоты конуса подвесного бака :0.877
Расчётное значение длины цилиндра подвесного бака :0.363
Вывод:
В сравнении с вариантом, когда условие R=H не выполняется, общая площадь поверхности бака почти не изменилась. Этот вариант компоновки является оптимальным, что подтверждает и практика.
Численные значения приведены для примера, в каждом конкретном случае нужно учитывать особенности конструкции.
Измерение уровня топлива в подвесном топливном баке
Работа реактивного двигателя зависит от расхода подаваемого топлива, который корректируется по уровню в баке. Поэтому, измерение уровня топлива в баке является важным технологическим параметром.
В не сбрасываемом топливном баке измерение уровня топлива осуществляется датчиками, установленными в прямом канале, верхний открытый конец которого расположен над уровнем топлива, которое заполняет канал за счёт давления наддува Po.
Вертикальный канал и топливный бак являются сообщающими сосудами. Снижая уровень топлива в баке, уровень топлива уменьшается в канале. Когда уровень топлива в канале достигает датчика, происходит активация датчика. Сигнал поступает в систему управления топливом.
Таким образом, уровень топлива в канале определяет уровень топлива в баке. Проблема в том, что свободная поверхность топлива не совпадает в канале и резервуаре. Ошибка измерения уровня топлива приводит к неэффективному расходу топлива.

Уровень топлива в баке изменяется согласно соотношения:

где: Ho – начальный уровень топлива в баке; V– скорость подачи топлива; t – время.
Для дальнейшего анализа зависимости скорости подачи топлива от времени воспользуемся соотношением, полученным в публикации [2]:

где: y – координаты свободной поверхности топлива в измерительном канале; L– коэффициент трения жидкости о стенки цилиндрического измерительного канала; R – радиус цилиндрического измерительного канала; g – ускорение свободного падения.
Начальные условия к дифференциальному уравнению (1) имеют вид:
y(0)=Ho, dy/dt=0.
Для численного решения дифференциального уравнения (1) средствами Python, введём следующие обозначения:

Изменение средней скорости топлива в измерительном канале.
# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
R=0.0195
H=8.2
g=9.8
L=4.83*10**-2
V=0.039
def f(y,t):
y1,y2=y
return [y2,-g+(g*(H-V*t)/y1)+((L/(4*R))*y2**2)]
t = np.arange(0,200,0.01)
y0=[H,0]
[y1,y2]=odeint(f,y0,t,full_output=False).T
plt.title("Изменение средней скорости топлива \n в измерительном канале")
plt.xlabel("t,s")
plt.ylabel("U,m/s ")
plt.plot(t,y2)
plt.grid(True)
plt.show()Получим:

Уровни топлива в измерительном канале и в баке.
# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
R=0.0195
H=8.2
g=9.8
L=4.83*10**-2
V=0.039
def f(y,t):
y1,y2=y
return [y2,-g+(g*(H-V*t)/y1)+((L/(4*R))*y2**2)]
t = np.arange(0,10,0.01)
y0=[H,0]
[y1,y2]=odeint(f,y0,t,full_output=False).T
plt.title('Изменение уровня топлива ')
plt.ylabel('H,m')
plt.ylabel('t,s')
plt.plot(t,y1,"b",linewidth=2,label='Уровень топлива в измерительном канале')
y=H-V*t
plt.plot(t,y,"--r",linewidth=2,label='Уровень топлива в баке')
plt.grid(True)
plt.legend(loc='best')
plt.show()Получим:

Ошибка измерения уровня топлива.
# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
R=0.0195
H=8.2
g=9.8
L=4.83*10**-2
V=0.039
def f(y,t):
y1,y2=y
return [y2,-g+(g*(H-V*t)/y1)+((L/(4*R))*y2**2)]
t = np.arange(0,200,0.01)
y0=[H,0]
[y1,y2]=odeint(f,y0,t,full_output=False).T
plt.title('Ошибка измерения уровня топлива ')
plt.ylabel('d,m')
plt.xlabel('t,s')
d=y1-(H-V*t)
plt.plot(t,d)
plt.grid(True)
plt.show()Получим:
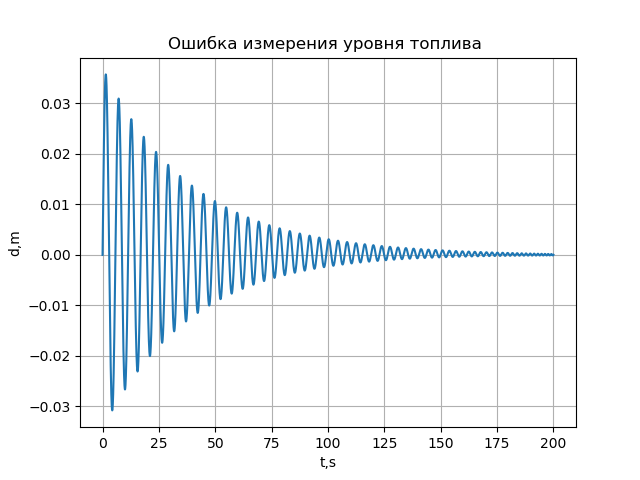
Вывод:
Приведенная математическая модель позволяет оценить погрешность измерения уровня топлива в баках самолётов.
Для ракеты нужно учитывать флуктуацию(колебания) жидкости в топливном баке ракеты. Такие флуктуации визуально показаны и в публикации [3].
Для учёта флуктуации топлива в баке, возможно рассмотрение и такой упрощённой модели:
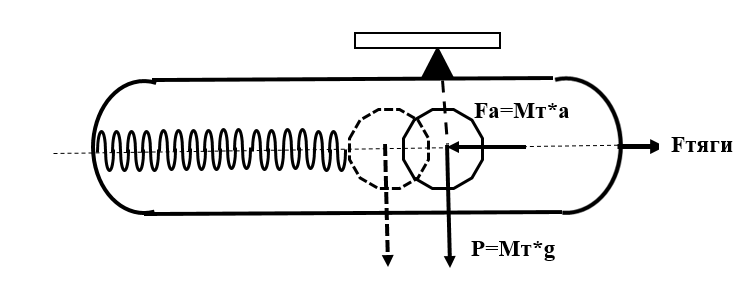
Жидкость рассматривается как сосредоточенная убывающая масса с приведенным рассеиванием и жёсткостью. Но это тема уже другой статьи.
Выводы:
1. В статье на примере оптимизации формы подвесных топливных баков продемонстрированы возможности Python по численной оптимизации с несколькими ограничениями.
2. В статье на примере решения не классического дифференциального уравнения продемонстрированы возможности решения таких уравнений средствами Python.
3. Полученные решения могут использоваться и в учебных целях, не обременяя школу или Вуз покупкой Mathcad или других дорогостоящих пакетов.
Ссылки: