Информацию о состоянии окружающей среды или, например, некоторого объекта управления можно получать, измеряя текущие значения параметров, характеризующих те или иные свойства среды или объекта. Для получения, обработки и передачи такой информации техническими средствами, значение измеряемого параметра необходимо преобразовать автоматическими измерительными устройствами в сигнал измерительной информации. Для этого реализуют информационно-измерительный канал (ИИК), как совокупность технических средств, каждое из которых будет выполнять свою определённую функцию, начиная от восприятия измеряемой величины и заканчивая получением измерительной информации в форме, удобной для восприятия человеком или для дальнейшей её обработки. И всё бы хорошо, да вот по пути следования информации на полезный сигнал y(t) измерительной информации накладывается помеха e(t) – случайная функция времени, которая может моделировать и случайную погрешность измерительного преобразователя, и электрические наводки в соединительных проводах, и случайные пульсации измеряемого параметра, и другие факторы.
Исходя из этого, возникает задача первичной обработки информации в ИИК – фильтрация сигнала y(t) измерительной информации от случайной помехи e(t). В основном, методы фильтрации основаны на различии частотных спектров функций y(t) и e(t), и помеху считают более высокочастотной.
Синтез оптимального реализуемого фильтра является сложной задачей, для решения которой необходимо точное задание характеристик полезного сигнала и помехи. Поэтому на практике обычно задают передаточную функцию фильтра и ограничиваются параметрическим синтезом, применяя простые алгоритмы фильтрации.
Методы фильтрации осуществляют, как на программном уровне, так и на аппаратном. Например, в датчике BMP280 (BOSCH) имеется возможность подключить БИХ-фильтр на аппаратном уровне, изменяя по необходимости коэффициент фильтрации k, [1].
Фильтры с бесконечной импульсной характеристикой относятся к рекурсивным фильтрам и вычисляют выходной сигнал на основании значений предыдущих входных и выходных отсчётов. Теоретически, импульсная характеристика БИХ-фильтра никогда не достигает нуля, поэтому выход получается бесконечным по длительности.
В общем виде, алгоритм фильтрации одномерного скалярного цифрового фильтра запишем, как [2]:
![$y[n] = T(x[n],x[n-1],…,x[n-M],y[n-1],…,y[n-N],n)$](https://habrastorage.org/getpro/habr/formulas/b8a/bf2/da6/b8abf2da66287da3a0e95b7d12889bbe.svg) , (1),
, (1),
где T – скалярная функция одной переменной.
Функция T зависит от текущего входного сигнала x[n], и предыдущих: M отсчётов входного сигнала и N отсчётов выходного сигнала
и N отсчётов выходного сигнала 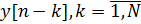
Выход БИХ-фильтра описывают разностным уравнением вида:
 (2),
(2),
где x[n], y[n] – вход и выход фильтра, соответственно, { } – набор прямых коэффициентов, M – число прямых коэффициентов, {
} – набор прямых коэффициентов, M – число прямых коэффициентов, { } – набор обратных коэффициентов, N – число обратных коэффициентов.
} – набор обратных коэффициентов, N – число обратных коэффициентов.
Применяя z-преобразование к обеим сторонам уравнения (2), получим:
 (3).
(3).
Тогда передаточная функция фильтра будет выглядеть следующим образом:
 (4)
(4)
В общем виде алгоритм фильтрации одномерного скалярного стационарного рекурсивного фильтра выглядит так:
![$y[n] = T(x[n],y[n-1])$](https://habrastorage.org/getpro/habr/formulas/5ad/76d/3fb/5ad76d3fb88ad5b313423e5472597674.svg) . (5)
. (5)
Запишем теперь разностное уравнение для БИХ-фильтра в виде [1]:
 (6),
(6),
где k – коэффициент фильтра;
или
![$y[n]=ay[n-1]+bx[n]$](https://habrastorage.org/getpro/habr/formulas/d2f/678/2e0/d2f6782e06362db1ef64568d26eb7321.svg) (7),
(7),
где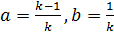 – обратный и прямой коэффициенты фильтра, соответственно.
– обратный и прямой коэффициенты фильтра, соответственно.
Из (7) очевидно, что при k=1 выходной сигнал фильтра будет повторять входной, и при увеличении коэффициента фильтра k вес предыдущего фильтрованного сигнала стремится к 1, а вес измеренного значения стремится к 0.
Алгоритм (6) реализован на примере информационно-измерительного канала абсолютного атмосферного давления для датчика BMP280, на программном уровне в среде разработки Arduino Software (IDE), листинг 1. Электрическая схема подключений компонентов ИИК представлена на рис. 1. Общий вид прототипа ИИК абсолютного атмосферного давления представлен на рис. 2. В прототипе предусмотрена возможность изменять коэффициент фильтрации в диапазоне 1…50 с шагом 1, вращением ручки потенциометра. На экране знакового жидкокристаллического дисплея отображается измеренное значение давления (при k = 1) или фильтрованное значение (при k = 2…50), и значение коэффициента фильтрации k.
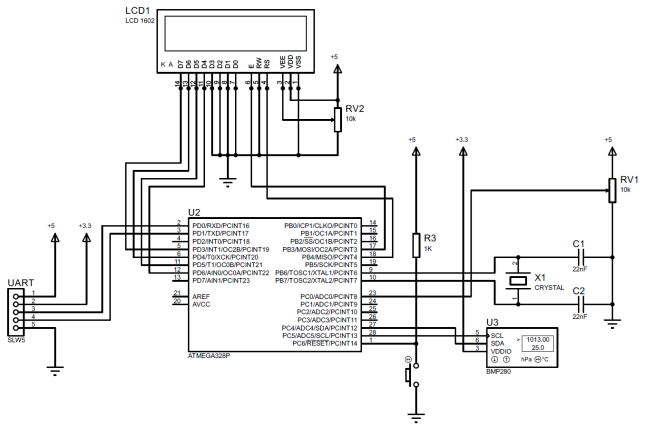
Рис. 1 – Электрическая схема подключений компонентов прототипа ИИК

Рис. 2 – Общий вид прототипа ИИК
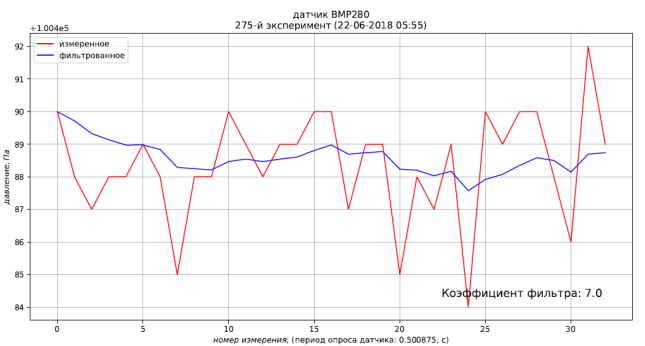
На листинге 2 представлен Python-cкрипт для исследования БИХ-фильтров. Коэффициент фильтрации k прописываем в скрипте. Измеренные значения давления последовательно считываются с виртуального COM-порта и фильтруются. В графическое окно и на консоль выводятся измеренные и фильтрованные значения измеряемого параметра в реальном режиме времени. Результаты эксперимента записываются таблицей в файл, а в графическое окно выводятся временные графики измеренных и фильтрованных значений.

Приведенный алгоритм фильтрации очень прост в программной реализации и, практически, может быть использован в ИИК, подобных рассмотренному в этой статье.
В работе принимал участие Лосихин Д.А., с.в. каф. КИТиМ.
Исходя из этого, возникает задача первичной обработки информации в ИИК – фильтрация сигнала y(t) измерительной информации от случайной помехи e(t). В основном, методы фильтрации основаны на различии частотных спектров функций y(t) и e(t), и помеху считают более высокочастотной.
Синтез оптимального реализуемого фильтра является сложной задачей, для решения которой необходимо точное задание характеристик полезного сигнала и помехи. Поэтому на практике обычно задают передаточную функцию фильтра и ограничиваются параметрическим синтезом, применяя простые алгоритмы фильтрации.
Методы фильтрации осуществляют, как на программном уровне, так и на аппаратном. Например, в датчике BMP280 (BOSCH) имеется возможность подключить БИХ-фильтр на аппаратном уровне, изменяя по необходимости коэффициент фильтрации k, [1].
БИХ-фильтр
Фильтры с бесконечной импульсной характеристикой относятся к рекурсивным фильтрам и вычисляют выходной сигнал на основании значений предыдущих входных и выходных отсчётов. Теоретически, импульсная характеристика БИХ-фильтра никогда не достигает нуля, поэтому выход получается бесконечным по длительности.
В общем виде, алгоритм фильтрации одномерного скалярного цифрового фильтра запишем, как [2]:
где T – скалярная функция одной переменной.
Функция T зависит от текущего входного сигнала x[n], и предыдущих: M отсчётов входного сигнала
 и N отсчётов выходного сигнала
и N отсчётов выходного сигнала 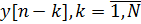
Выход БИХ-фильтра описывают разностным уравнением вида:
 (2),
(2),где x[n], y[n] – вход и выход фильтра, соответственно, {
Применяя z-преобразование к обеим сторонам уравнения (2), получим:
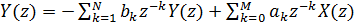 (3).
(3).Тогда передаточная функция фильтра будет выглядеть следующим образом:
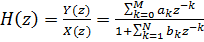 (4)
(4)Алгоритм фильтрации одномерного БИХ-фильтра
В общем виде алгоритм фильтрации одномерного скалярного стационарного рекурсивного фильтра выглядит так:
Запишем теперь разностное уравнение для БИХ-фильтра в виде [1]:
 (6),
(6),где k – коэффициент фильтра;
или
где
 – обратный и прямой коэффициенты фильтра, соответственно.
– обратный и прямой коэффициенты фильтра, соответственно.Из (7) очевидно, что при k=1 выходной сигнал фильтра будет повторять входной, и при увеличении коэффициента фильтра k вес предыдущего фильтрованного сигнала стремится к 1, а вес измеренного значения стремится к 0.
Алгоритм (6) реализован на примере информационно-измерительного канала абсолютного атмосферного давления для датчика BMP280, на программном уровне в среде разработки Arduino Software (IDE), листинг 1. Электрическая схема подключений компонентов ИИК представлена на рис. 1. Общий вид прототипа ИИК абсолютного атмосферного давления представлен на рис. 2. В прототипе предусмотрена возможность изменять коэффициент фильтрации в диапазоне 1…50 с шагом 1, вращением ручки потенциометра. На экране знакового жидкокристаллического дисплея отображается измеренное значение давления (при k = 1) или фильтрованное значение (при k = 2…50), и значение коэффициента фильтрации k.
Листинг 1
//ИИК абсолютного атмосферного давления (температуры)
//цель - исследование БИХ-фильтров
//https://github.com/orgua/iLib/blob/master/src/i2c.h
#include "i2c.h"
//https://github.com/orgua/iLib/blob/master/src/i2c_BMP280.h
#include "i2c_BMP280.h"
//https://github.com/arduino-libraries/LiquidCrystal
#include <LiquidCrystal.h>
//https://github.com/orgua/iLib/tree/master/examples/i2c_BMP280
BMP280 bmp280;
const int rs = 12, en = 11, d4 = 6, d5 = 5, d6 = 4, d7 = 3;
//const int rs = PB4, en = PB3, d4 = PD6, d5 = PD5, d6 = PD4, d7 = PD3;
LiquidCrystal lcd(rs, en, d4, d5, d6, d7);
float pascal_f = 100500;
float filter_K = 1;
const int analogInPin = A0; //аналоговый вход от потенциометра
int sensorValue = 0; //сигнал от потенциометра
int outputValue = 0;
void setup()
{
Serial.begin(9600);
//Serial.print("Probe BMP280: ");
if (bmp280.initialize()) {
//Serial.println("Sensor found");
;
}
else
{
Serial.println("Sensor missing");
while (1) {}
}
bmp280.setEnabled(0);
bmp280.triggerMeasurement();
bmp280.setFilterRatio(0);
lcd.begin(16, 2);
lcd.setCursor(0, 0);
lcd.print("measure");
lcd.setCursor(7, 1);
lcd.print("Pa");
lcd.setCursor(10, 0);
lcd.print("filter");
}
void loop()
{
float temperature;
float pascal, hpascal;
sensorValue = analogRead(analogInPin);
outputValue = map(sensorValue, 0, 1023, 1, 50);
filter_K = outputValue;
bmp280.awaitMeasurement();
bmp280.getTemperature(temperature);
temperature -= 1.7; //поправка
bmp280.getPressure(pascal);
pascal -= 50;//поправка
hpascal = pascal/100.;
bmp280.triggerMeasurement();
pascal_f = (pascal_f * (filter_K - 1) + pascal) / filter_K; //(6)
Serial.println(pascal_f,0);
if(pascal_f < 100000)
lcd.setCursor(6, 1);
lcd.print(" ");
lcd.setCursor(0, 1);
lcd.print(pascal_f,0);
if(filter_K < 10)
lcd.setCursor(13, 1);
lcd.print(" ");
lcd.setCursor(10, 1);
lcd.print(filter_K,1);
delay(300);
}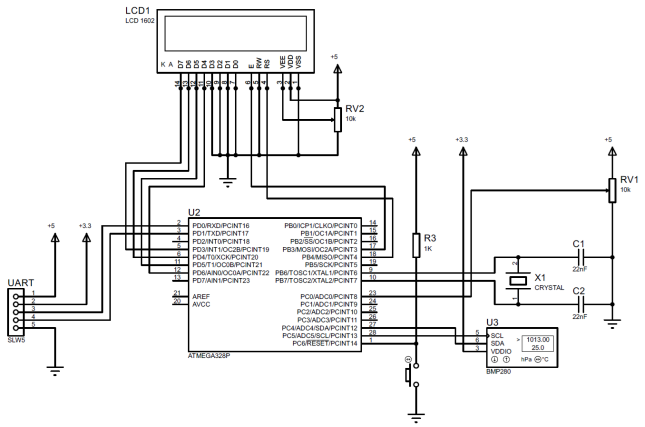
Рис. 1 – Электрическая схема подключений компонентов прототипа ИИК

Рис. 2 – Общий вид прототипа ИИК
Python-cкрипт для исследования БИХ-фильтров
На листинге 2 представлен Python-cкрипт для исследования БИХ-фильтров. Коэффициент фильтрации k прописываем в скрипте. Измеренные значения давления последовательно считываются с виртуального COM-порта и фильтруются. В графическое окно и на консоль выводятся измеренные и фильтрованные значения измеряемого параметра в реальном режиме времени. Результаты эксперимента записываются таблицей в файл, а в графическое окно выводятся временные графики измеренных и фильтрованных значений.
Листинг 2
import numpy as np
import matplotlib.pyplot as plt
import serial
from drawnow import drawnow
import datetime, time
k = 6.0 #коэффициент фильтрации + 1
filter_K = 1 + k
#вывод выборки в графическое окно
def cur_graf():
plt.title("BMP280")
plt.ylim( 100450, 100510 )
plt.plot(nw, lw1, "r.-", label='измеренное')
plt.plot(nw, lw1f, "b.-", label='фильтрованное')
plt.legend(loc='best')
plt.ylabel(r'$давление, Па$')
plt.xlabel(r'$номер \ измерения$')
plt.grid(True)
#вывод всех списков в графическое окно
def all_graf():
plt.close()
fig=plt.figure()
ax = fig.add_subplot(111)
fig.subplots_adjust(top=0.85)
ax.set_title("датчик BMP280\n" +
str(count_v) + "-й эксперимент " +
"(" + now.strftime("%d-%m-%Y %H:%M") + ")")
ax.set_ylabel(r'$давление, Па$')
ax.set_xlabel(r'$номер \ измерения$' +
'; (период опроса датчика: {:.6f}, c)'.format(Ts))
ax.text(0.95, 0.03,
"Коэффициент фильтра: " + str(filter_K) + "\n",
verticalalignment='bottom', horizontalalignment='right',
transform=ax.transAxes,
color='black', fontsize=14)
plt.plot( n, l1, "r-", label='измеренное')
plt.plot( n, l1f, "b-", label='фильтрованное')
plt.legend(loc='best')
plt.grid(True)
plt.show()
#определяем количество измерений
# общее количество измерений
str_m = input("введите количество измерений: ")
m = eval(str_m)
# количество элементов выборки
mw = 16
#настроить параметры последовательного порта
ser = serial.Serial()
ser.baudrate = 9600
port_num = input("введите номер последовательного порта: ")
ser.port = 'COM' + port_num
ser
#открыть последовательный порт
try:
ser.open()
ser.is_open
print("соединились с: " + ser.portstr)
except serial.SerialException:
print("нет соединения с портом: " + ser.portstr)
raise SystemExit(1)
#определяем списки
l1 = [] # для значений давления
l1f = [] # для фильтрованных значений давления
t1 = [] # для значений моментов времени
lw1 = [] # для значений выборки давления
lw1f= [] # для фильтрованных значений выборки давления
n = [] # для значений моментов выборки
nw = [] # для значений выборки моментов времени
#подготовить файлы на диске для записи
filename = 'count.txt'
in_file = open(filename,"r")
count = in_file.read()
count_v = eval(count) + 1
in_file.close()
in_file = open(filename,"w")
count = str(count_v)
in_file.write(count)
in_file.close()
filename = count + '_' + filename
out_file = open(filename,"w")
#вывод информации для оператора на консоль
print("\nпараметры:\n")
print("n - номер измерения;")
print("P - давление, Па;")
print("\nизмеряемые значения величины давления\n")
print('{0}{1}\n'.format('n'.rjust(4),'P'.rjust(10)))
#считывание данных из последовательного порта
#накопление списков
#формирование текущей выборки
#вывод значений текущей выборки в графическое окно
i = 0
while i < m:
n.append(i)
nw.append(n[i])
if i >= mw:
nw.pop(0)
line1 = ser.readline().decode('utf-8')[:-2]
t1.append(time.time())
if line1:
l1.append(eval(line1))
lw1.append(l1[i])
if i :
l1f.append( (l1f[i-1]*(filter_K - 1) + l1[i])/filter_K ) #(6)
lw1f.append(l1f[i])
else :
l1f.append(l1[i])
lw1f.append(l1f[i])
if i >= mw:
lw1.pop(0)
lw1f.pop(0)
print('{0:4d} {1:10.2f} {2:10.2f}'.format(n[i],l1[i],l1f[i]) )
drawnow(cur_graf)
i += 1
#закрыть последовательный порт
ser.close()
ser.is_open
time_tm = t1[m - 1] - t1[0]
print("\nпродолжительность времени измерений: {0:.3f}, c".format(time_tm))
Ts = time_tm / (m - 1)
print("\nпериод опроса датчика: {0:.6f}, c".format(Ts))
#запись таблицы в файл
print("\nтаблица находится в файле {}\n".format(filename))
for i in np.arange(0,len(n),1):
count = str(n[i]) + "\t" + str(l1[i]) + "\n"
out_file.write(count)
#закрыть файл с таблицей
out_file.close()
out_file.closed
#получить дату и время
now = datetime.datetime.now()
#вывести график в графическое окно
all_graf()
end = input("\nнажмите Ctrl-C, чтобы выйти ")
Результаты эксперимента
введите количество измерений: 33
введите номер последовательного порта: 6
соединились с: COM6
параметры:
n - номер измерения;
P - давление, Па;
измеряемые значения величины давления
n P
0 100490.00 100490.00
1 100488.00 100489.71
2 100487.00 100489.33
3 100488.00 100489.14
4 100488.00 100488.97
…
30 100486.00 100488.14
31 100492.00 100488.70
32 100489.00 100488.74
продолжительность времени измерений: 16.028, c
период опроса датчика: 0.500875, c
таблица находится в файле 275_count.txt
нажмите Ctrl-C, чтобы выйти


Выводы
Приведенный алгоритм фильтрации очень прост в программной реализации и, практически, может быть использован в ИИК, подобных рассмотренному в этой статье.
В работе принимал участие Лосихин Д.А., с.в. каф. КИТиМ.