Предисловие
Всем доброго времени суток. Представляю вашему вниманию следующую статью из серии освещения новых и малоизвестных эвристических методов оптимизации. Сегодняшний пост своим появлением обязан Эсмату Рашеди, Исааку Ньютону и гравитации.

Историческая справка
Гравитационный поиск (GS) является очень молодым алгоритмом. Появился он в 2009 году и являлся логическим развитием метода центральной силы. Основу GS составляют законы гравитации и взаимодействия масс. В принципе, данный алгоритм похож на методы роя частиц (Particle Swarm Optimization — PSO), так как базируется на развитии многоагентной системы.
Стратегия
GS оперирует двумя законами:
- тяготения: каждая частица притягивает другие и сила притяжения между двумя частицами прямо пропорциональна произведению их масс и обратно пропорциональна расстоянию между ними (следует обратить внимание на то, что в отличие от Всемирного закона тяготения используется не квадрат расстояния; Рашеди объясняет это тем, что во всех тестах это дает лучшие результаты, оставим это на его совести)

- движения: текущая скорость любой частицы равна сумме части скорости в предыдущий момент времени и изменению скорости, которое равно силе, с которой воздействует система на частицу, деленной на инерциальную массу частицы.
Имея в арсенале эти два закона, метод работает по следующему плану:
- генерация системы случайным образом,
- определение приспособленности каждой частицы,
- обновление значений гравитационной постоянной, лучшей и худшей частиц, а так же масс,
- подсчет результирующей силы в различных направлениях,
- подсчет ускорений и скоростей,
- обновление позиций частиц,
- повторений шагов 2 — 6 до выполнения критерия окончания (либо превышение максимального количества итераций, либо слишком малой изменение позиций, либо
что вашей душе угоднолюбой другой осмысленный критерий).
Для тех, кого интересует более подробное описание алгоритма
Итак, у нас есть некоторая функция, которую необходимо минимизировать:  . Кроме этого, есть область
. Кроме этого, есть область 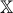 , в которой генерируются начальные позиции частиц. В соответствии с планом работы GS, начинается все с генерации системы частиц
, в которой генерируются начальные позиции частиц. В соответствии с планом работы GS, начинается все с генерации системы частиц 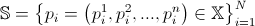 , где
, где  — максимальное количество частиц в системе.
— максимальное количество частиц в системе.
Сила, действующая в момент времени на
на 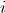 -ю частицу со стороны
-ю частицу со стороны 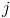 -й, рассчитывается по формуле
-й, рассчитывается по формуле 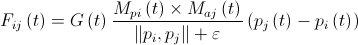 , где
, где 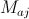 — активная гравитационная масса
— активная гравитационная масса 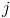 -й частицы,
-й частицы,  — пассивная гравитационная масса
— пассивная гравитационная масса 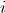 -й частицы,
-й частицы, 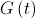 — гравитационная постоянная в соответствующий момент времени,
— гравитационная постоянная в соответствующий момент времени,  — малая константа,
— малая константа, 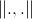 — евклидово расстояние между частицами.
— евклидово расстояние между частицами.
Чтобы алгоритм был не детерминированным, а стохастическим, в формулу расчета результирующей силы добавляются случайные величины
добавляются случайные величины  (равномерно распределенные от нуля до единицы). Тогда результирующая сила равна
(равномерно распределенные от нуля до единицы). Тогда результирующая сила равна 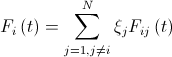 .
.
Посчитаем ускорения и скорости: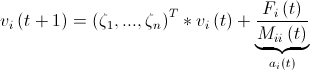 , где
, где  — операция покомпонентного умножения векторов,
— операция покомпонентного умножения векторов,  — случайная величина, равномерно распределенная от нуля до единицы,
— случайная величина, равномерно распределенная от нуля до единицы, 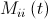 — инертная масса
— инертная масса 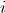 -й частицы.
-й частицы.
Остается пересчитать положение частиц. Сделать это очень просто: .
.
К текущему моменту осталось два вопроса: как изменяется гравитационная постоянная и как рассчитывать массы частиц. Значение гравитационной постоянной должно определяться монотонно убывающей функцией, зависящей от начального значений постоянной и момента времени
и момента времени  , т.е.
, т.е. 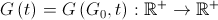 .
.
Например, можно брать следующие функции:
Теперь можно приступить к заключительной части повествования: к пересчету масс. В простейшем случае все три массы (пассивная, активная и инерциальная) приравниваются: . Тогда значение масс можно пересчитать по формуле:
. Тогда значение масс можно пересчитать по формуле: 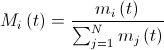 , где
, где 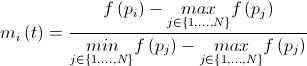 .
.
Конечно, можно рассчитывать массы исходя из их физического значения, тем не менее Рашеди об этом не говорит (и никто из авторов, которых я смог найти).
 . Кроме этого, есть область
. Кроме этого, есть область 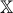 , в которой генерируются начальные позиции частиц. В соответствии с планом работы GS, начинается все с генерации системы частиц
, в которой генерируются начальные позиции частиц. В соответствии с планом работы GS, начинается все с генерации системы частиц 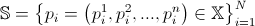 , где
, где  — максимальное количество частиц в системе.
— максимальное количество частиц в системе.Сила, действующая в момент времени
 на
на 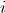 -ю частицу со стороны
-ю частицу со стороны 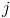 -й, рассчитывается по формуле
-й, рассчитывается по формуле 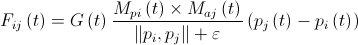 , где
, где 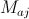 — активная гравитационная масса
— активная гравитационная масса 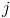 -й частицы,
-й частицы,  — пассивная гравитационная масса
— пассивная гравитационная масса 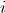 -й частицы,
-й частицы, 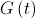 — гравитационная постоянная в соответствующий момент времени,
— гравитационная постоянная в соответствующий момент времени,  — малая константа,
— малая константа, 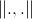 — евклидово расстояние между частицами.
— евклидово расстояние между частицами.Чтобы алгоритм был не детерминированным, а стохастическим, в формулу расчета результирующей силы
 добавляются случайные величины
добавляются случайные величины  (равномерно распределенные от нуля до единицы). Тогда результирующая сила равна
(равномерно распределенные от нуля до единицы). Тогда результирующая сила равна 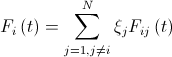 .
.Посчитаем ускорения и скорости:
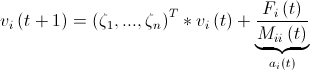 , где
, где  — операция покомпонентного умножения векторов,
— операция покомпонентного умножения векторов,  — случайная величина, равномерно распределенная от нуля до единицы,
— случайная величина, равномерно распределенная от нуля до единицы, 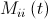 — инертная масса
— инертная масса 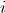 -й частицы.
-й частицы.Остается пересчитать положение частиц. Сделать это очень просто:
 .
.К текущему моменту осталось два вопроса: как изменяется гравитационная постоянная и как рассчитывать массы частиц. Значение гравитационной постоянной должно определяться монотонно убывающей функцией, зависящей от начального значений постоянной
 и момента времени
и момента времени  , т.е.
, т.е. 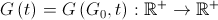 .
.Например, можно брать следующие функции:
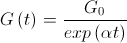 , где
, где 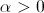 :
:  ,
, , где
, где  :
: 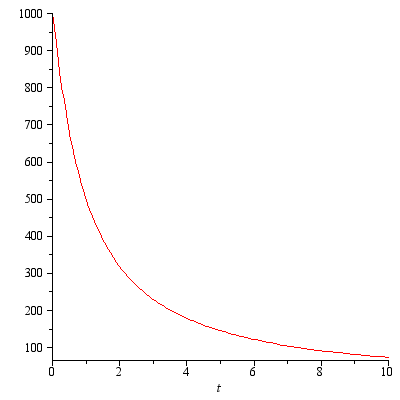 ,
,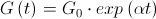 , где
, где  :
: 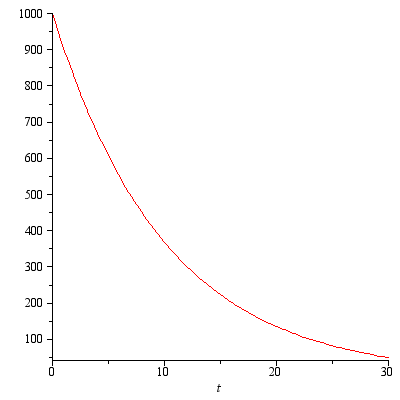 .
.
Теперь можно приступить к заключительной части повествования: к пересчету масс. В простейшем случае все три массы (пассивная, активная и инерциальная) приравниваются:
 . Тогда значение масс можно пересчитать по формуле:
. Тогда значение масс можно пересчитать по формуле: 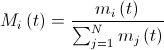 , где
, где 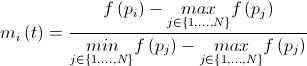 .
.Конечно, можно рассчитывать массы исходя из их физического значения, тем не менее Рашеди об этом не говорит (и никто из авторов, которых я смог найти).
Pros and Cons
Плюсы
- как и в случае с гармоническим поиском простота реализации,
- на практике метод точнее, чем генетические алгоритмы с вещественным кодированием и классический PSO,
- большая скорость сходимости, чем у генетических алгоритмов с вещественным кодированием и классического PSO.
Минусы
- не самая большая скорость за счет необходимости пересчета многих параметров,
- большая часть достоинств теряется при оптимизации мультимодальных функций (особенно больших размерностей), так как метод начинает быстро сходиться к некоторому локальному оптимуму, из которого сложно выбраться, так как не предусмотрены процедуры, похожие на мутации в генетических алгоритмах.
Использованные источники
- Работа самого Рашеди (на случай, если у кого-то есть доступ к их библиотеке),
- Прекрасная статья Карпенко, в которой коротко описаны многие алгоритмы (на нее в дальнейшем не раз буду ссылаться),
- Подборка статей.
Может пригодиться
Послесловие
На этом, пожалуй, знакомство с методом гравитационного поиска стоит закончить. Очень надеюсь, что данный пост получился лучше предыдущего. Остается лишь проголосовать за тему следующего поста.
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Какой алгоритм описать в следующем посте?
38%Grenade Explosion Method38
24%Fireworks Algorithm24
38%Electromagnetism-like Algorithm38
Проголосовали 100 пользователей. Воздержались 76 пользователей.
