Наверное каждый из нас когда-нибудь играл, или по крайней мере пробовал играть в «Сапёр» («MineSweeper»). Логика игры проста, но в свое время за алгоритм ее прохождения даже обещали вознаграждение. В моем боте логика имеет три алгоритма, которые используются в зависимости от ситуации на поле. Основной алгоритм позволяет находить все ячейки со 100- и 0-процентной вероятностью нахождения мины. Используя только этот алгоритм и открывая наугад произвольные ячейки при отсутствии достоверного решения в стандартном сапере на уровне «Эксперт» можно достичь 33% выигрышей. Однако некоторые дополнительные алгоритмы позволяют поднять это значение до 44% (Windows 7).
Основной алгоритм состоит в следующем. Неизвестные ячейки (класс Cell), прилегающие к одной открытой ячейке формируются в группу (класс Group), в которую записывается также значение ячейки, к которой она прилегает.

На рисунке обозначены четыре группы, некоторые из которых пересекаются, а некоторые и вовсе содержат другие группы. Обозначим (123,1) — группа состоит из ячеек 1,2 и 3, и при этом в них находится 1 мина. (5678,2) — в четырех ячейках находятся 2 мины.
Для начала нужно преобразовать группы. Для этого:
В итоге у нас получатся три вида групп.
Но часто встречаются ситуации, когда нет достоверного решения ситуации. Тогда на помощь приходит следующий алгоритм. Его суть состоит в использовании теории вероятности. Алгоритм работает в два этапа:
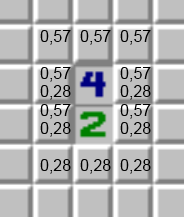
Для вычисления вероятности нахождения мины в ячейке рядом с несколькими открытыми ячейками используем формулу расчета вероятности хотя бы одного события:

Однако следует помнить, что сумма вероятностей в каждой группе ячеек должна быть равна количеству мин в группе. Поэтому все значения в каждой группе нужно домножить так, чтобы в итоге их сумма была равна числу мин. Это число равно количеству мин в группе, деленое на текущую сумму вероятностей ячеек группы:
Теперь те ячейки, что имели вероятность 0,57 имеют 0,485, а те, что 0,69 → 0,618
Подобный расчет для второй группы проводим уже с учетом корректировки от предыдущей.
Видим, что вероятность в общих ячейках опять изменилась, поэтому подобное уравнивание для каждой группы нужно повторить несколько раз, пока система не придет к некоторым стабильным значениям, которые и будут истинными вероятностями нахождения мин в ячейках.
… и т. д.

Остается только выбрать одну из ячеек с минимальной вероятностью и сделать ход.
На заключительном этапе игры большую роль играет количество не помеченных мин. Зная это количество можно перебором подставлять их в неизвестные ячейки, и отмечать подходящие варианты. В процессе перебора подходящих вариантов для каждой ячейки считаем количество пометок. Разделив получившиеся значения на общее число пометок получаем вероятность нахождения мин для каждой ячейки. Например в этой ситуации, имеющей, казалось бы только одно достоверное решение последний метод (LastTurns) нашел 3 ячейки с 0% вероятности нахождения мины.
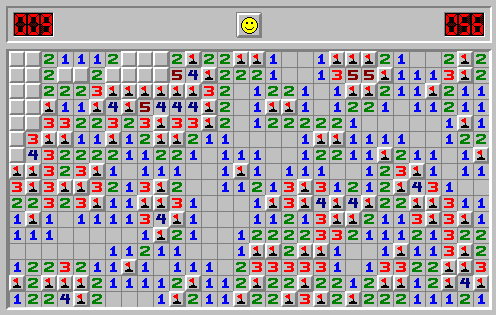
LastTurns(9,21) проверил 144 подходящих комбинаций из 293930 возможных и нашел 3 ячеек с минимальной вероятностью 0 %
C точки зрения сложности понимания идеи этот метод самый легкий, поэтому подробно разбирать его пока не буду.
На практике при достаточном числе выборок расчетные и фактические значения вероятностей нахождения мины в ячейке почти совпадают. В следующей таблице приведены результаты работы бота на «Сапер» под Windows XP в течение одной ночи, где
Большое расхождение в области 20-22% вероятно связано с тем, что часто этот процент имели ячейки, не имеющие рядом уже открытые (например в начале игры), и «Сапер» подстраивался под игрока, иногда убирая из-под открываемой ячейки мину. Алгоритм работы был реализован на java и опробован на стандартном сапере Windows (7 и ХР), приложении в VK и на игруне. К слову сказать, после нескольких дней «технических неполадок» при доступе на мой аккаунт с моего IP игрун изменил правила вознаграждения за открытие части поля: изначально возвращал 10% ставки за 10% открытого поля, потом 5%, потом 2%, а когда я перестал играть, то вернул 5%.
Основной алгоритм
Основной алгоритм состоит в следующем. Неизвестные ячейки (класс Cell), прилегающие к одной открытой ячейке формируются в группу (класс Group), в которую записывается также значение ячейки, к которой она прилегает.

На рисунке обозначены четыре группы, некоторые из которых пересекаются, а некоторые и вовсе содержат другие группы. Обозначим (123,1) — группа состоит из ячеек 1,2 и 3, и при этом в них находится 1 мина. (5678,2) — в четырех ячейках находятся 2 мины.
Для начала нужно преобразовать группы. Для этого:
- Сравниваем каждую группу с каждой последующей группой.
- Если группы одинаковые, то вторую удаляем.
- Если одна группа содержит другую, то вычитаем из большей меньшую. То есть было две группы (5678,2) и (5,1), стало (678,1) и (5,1); (2345,3) и (5,1) → (234,2) и (5,1)
- Пересекающиеся группы, например (123,1) и (234,2), преобразовываем по следующему принципу:
- Создаем новую группу из пересекающихся ячеек (23,?)
- Рассчитываем количество мин в новой группе, равное количеству мин в группе с большим числом мин (234,2) минус оставшееся количество ячеек в другой группе после отделения пересекающихся ячеек (1,?). То есть 2-1 = 1. Получаем (23,1)
- Если рассчитанное количество мин в новой группе (23,1) не равно количеству мин в группе с меньшим количеством мин (123,1), то прекращаем преобразование
- Вычитаем из обоих пересекающихся групп новообразованную группу. (123,1)-(23,1) = (1,0), (234,2)-(23,1) = (4,1).
- Добавляем новообразованную группу в список групп
- Повторяем с п. 1 до тех пор, пока не будет производиться никаких изменений
Метод создания и преобразования групп
/** * Создает список групп ячеек, связанных одним значением открытого поля, а также разбивает их на более мелкие, удаляет повторяющиеся. */ private void setGroups() { groups.clear(); for (int x = 0; x < width; x++) for (int y = 0; y < height; y++) field[x][y].setGroup(groups); // создание групп boolean repeat; do{ repeat=false; for (int i = 0; i < groups.size() - 1; i++) { // проходим по списку групп Group groupI = groups.get(i); for (int j = i + 1; j < groups.size(); j++) { // сравниваем ее с остальными меньшими группами Group groupJ=groups.get(j); if (groupI.equals(groupJ)) // удаляем одинаковые группы {groups.remove(j--);break;} Group parent; // большая группа Group child; // меньшая группа if (groupI.size()>groupJ.size()) // определяем большую и меньшую группы по кол-ву ячеек {parent=groupI;child=groupJ;} else {child=groupI;parent=groupJ;} if (parent.contains(child)) { // если большая содержит меньшую parent.subtraction(child); // то вычитаем меньшую из большей repeat=true; // фиксируем факт изменения групп } else if (groupI.overlaps(groupJ) > 0) { // иначе если группы пересекаются if (groupI.getMines()>groupJ.getMines())// определяем большую и меньшую группы по кол-ву мин {parent=groupI;child=groupJ;} else {child=groupI;parent=groupJ;} Group overlap = parent.getOverlap(child);// то берем результат пересечения if (overlap != null) { // и если он имеет смысл (в результате пересечения выявились ячейки с 0% или 100%) groups.add(overlap); // то вносим соответствующие коррективы в список parent.subtraction(overlap); child.subtraction(overlap); repeat=true; } } } } } while(repeat); }
В итоге у нас получатся три вида групп.
- количество мин равно нулю
- количество мин равно количеству ячеек в группе
- ненулевое количество мин меньше количества ячеек в группе
Если нет достоверного решения
Но часто встречаются ситуации, когда нет достоверного решения ситуации. Тогда на помощь приходит следующий алгоритм. Его суть состоит в использовании теории вероятности. Алгоритм работает в два этапа:
- Определение вероятности в отдельных ячейках, учитывая влияние нескольких открытых ячеек
- Корректировка вероятностей, учитывая взаимное влияние групп с общими ячейками друг на друга

Для вычисления вероятности нахождения мины в ячейке рядом с несколькими открытыми ячейками используем формулу расчета вероятности хотя бы одного события:
Вероятность наступления события А, состоящего в появлении хотя бы одного из событий А1, А2,..., Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий. А=1- (1-A1)*(1-A2)*....*(1-An)В смежных ячейках после применения этой формулы результат равен 1-(1-0,57)*(1-0,28)=0,69.

Однако следует помнить, что сумма вероятностей в каждой группе ячеек должна быть равна количеству мин в группе. Поэтому все значения в каждой группе нужно домножить так, чтобы в итоге их сумма была равна числу мин. Это число равно количеству мин в группе, деленое на текущую сумму вероятностей ячеек группы:
4/(0,57+0,57+0,57+0,69+0,69+0,69+0,69)=0,895
0,57*0,895=0,485 0,69*0,895=0,618
Теперь те ячейки, что имели вероятность 0,57 имеют 0,485, а те, что 0,69 → 0,618
Подобный расчет для второй группы проводим уже с учетом корректировки от предыдущей.
2/(0,28+0,28+0,28+0,618+0,618+0,618+0,618)=0,604
0,28*0,604=0,169 0,618*0,604=0,373
Видим, что вероятность в общих ячейках опять изменилась, поэтому подобное уравнивание для каждой группы нужно повторить несколько раз, пока система не придет к некоторым стабильным значениям, которые и будут истинными вероятностями нахождения мин в ячейках.
4/(0,485+0,485+0,485+0,373+0,373+0,373+0,373)=1,357
0,485*1,357=0,658 0,373*1,357=0,506
2/(0,169+0,169+0,169+0,506+0,506+0,506+0,506)=0,79
0,169*0,79=0,134 0,506*0,79=0,4
… и т. д.

Остается только выбрать одну из ячеек с минимальной вероятностью и сделать ход.
Этот метод в коде
/** * Метод вносит корректировку в значения вероятностей нахождения мин в ячейках, учитывая взаимное влияние вероятностей соседних ячеек друг на друга */ private void correctPosibilities(){ Map<Cell,Double>cells= new HashMap<>(); // цикл устанавливает единое значение вероятности в каждой ячейке, учитывая различные значения вероятностей в ячейке от разных групп for (Group group : groups){ for (Cell cell: group.getList()){ Double value; if ((value=cells.get(cell))==null) // если ячейка еще не в мапе cells.put(cell,(double) group.getMines()/ group.size()); // то добавляем ее со значением из группы else //если она уже в мапе, то корректируем ее значение по теории вероятности cells.put(cell,Prob.sum(value,(double) group.getMines()/ group.size())); } } // цикл корректирует значения с учетом того, что сумма вероятностей в группе должна быть равна количеству мин в группе boolean repeat; do{ repeat=false; for (Group group : groups){ // для каждой группы List<Double> prob= group.getProbabilities(); // берем список вероятностей всех ячеек в группе в процентах Double sum=0.0; for (Double elem:prob)sum+=elem; // вычисляем ее сумму int mines= group.getMines()*100; // умножаем количество мин в группе на сто (из-за процентов) if (Math.abs(sum-mines)>1){ // если разница между ними велика, то проводим корректировку repeat=true; // фиксируем факт корректировки Prob.correct(prob,mines); // корректируем список for (int i=0;i< group.size();i++){ // заносим откорректированные значения из списка в ячейки double value= prob.get(i); group.getList().get(i).setPossibility(value); } } } } while (repeat); for (Cell cell:cells.keySet()){ // перестраховка if (cell.getPossibility()>99)cell.setPossibility(99); if (cell.getPossibility()<0)cell.setPossibility(0); } }
Последние ходы
На заключительном этапе игры большую роль играет количество не помеченных мин. Зная это количество можно перебором подставлять их в неизвестные ячейки, и отмечать подходящие варианты. В процессе перебора подходящих вариантов для каждой ячейки считаем количество пометок. Разделив получившиеся значения на общее число пометок получаем вероятность нахождения мин для каждой ячейки. Например в этой ситуации, имеющей, казалось бы только одно достоверное решение последний метод (LastTurns) нашел 3 ячейки с 0% вероятности нахождения мины.

LastTurns(9,21) проверил 144 подходящих комбинаций из 293930 возможных и нашел 3 ячеек с минимальной вероятностью 0 %
C точки зрения сложности понимания идеи этот метод самый легкий, поэтому подробно разбирать его пока не буду.
Его реализация
/** * Самостоятельный алгоритм расчета путем банального перебора. Можно использовать только если количество неизвестных ячеек не больше 30 * @return */ public ArrayList<Point> getLastTurns() { int minesLeft = countMinesLeft(); // количество оставшихся непомеченными мин ArrayList<Cell> unknownCells = getUnknownCells(); // список неизвестных ячеек int notOpened = unknownCells.size(); // количество неизвестных ячеек Integer[] combinations = new Sequence6().getSequensed(minesLeft, notOpened); // массив различных комбинаций из заданного количества мин в заданном количестве ячеек ArrayList<String> list = new ArrayList<String>(); // список возможных комбинаций for (int i = 0; i < combinations.length; i++) { // в этом цикле проходит подстановка мин из каждой комбинации и проверка на реальность такой игровой ситуации String combination = Integer.toBinaryString(combinations[i]); // преодбразование целого десятичного числа в двоичное, а затем в строку if (combination.length() < notOpened) { // добавляем необходимое количество "0" перед строковым выражением числа, чтобы длина строки равнялась количеству неизвестных ячеек String prefix = ""; for (int k = combination.length(); k < notOpened; k++) prefix += "0"; combination = prefix + combination; } for (int j = 0; j < notOpened; j++) { // расстановка мин по неизвестным ячейкам if (combination.charAt(j) == '1') unknownCells.get(j).setMine(); if (combination.charAt(j) == '0') unknownCells.get(j).setUnknown(); } if (test()) list.add(combination); // если при такой расстановке нет противоречий с известными ячейками, то заносим комбинацию в список возможных } clear(unknownCells); // возвращаем неизвестные ячейки в исходное состояние String[] comb = new String[list.size()]; list.toArray(comb); // преобразовываем список в массив, и далее работаем с массивом int[] possibilities2 = new int[notOpened]; // массив по числу неизвестных ячеек, содержащий количество вариантов, где может располагаться мина в заданной ячейке for (int i = 0; i < comb.length; i++) // цикл заполняет массив possibilities2[] for (int j = 0; j < notOpened; j++) if (comb[i].charAt(j) == '1') possibilities2[j]++; // если в комбинации в определенном месте есть мина, то увеличиваем соответствующий элемент массива на 1 int min = Integer.MAX_VALUE; ArrayList<Integer> minIndices = new ArrayList<>(); // список индексов с минимальным значением в possibilities2[] for (int i = 0; i < possibilities2.length; i++) { if (possibilities2[i] == min) minIndices.add(i); if (possibilities2[i] < min) { min = possibilities2[i]; minIndices.clear(); minIndices.add(i); } unknownCells.get(i).setPossibility(100*possibilities2[i]/comb.length); // устанавливаем найденные значения вероятностей в неизвестных ячейках } double minPossibility = 100.0 * possibilities2[minIndices.get(0)] / comb.length; System.out.println("LastTurns(" + minesLeft + "," + notOpened + ") проверил " + comb.length + " подходящих комбинаций из " + combinations.length + " возможных и нашел " + minIndices.size() + " ячеек" + " с минимальной вероятностью " + (int) minPossibility + " %"); ArrayList<Point> result = new ArrayList<Point>(minIndices.size());// список координат ячеек с минимальной вероятностью for (int index : minIndices) { result.add(unknownCells.get(index).getPoint()); } return result; }
Вывод
На практике при достаточном числе выборок расчетные и фактические значения вероятностей нахождения мины в ячейке почти совпадают. В следующей таблице приведены результаты работы бота на «Сапер» под Windows XP в течение одной ночи, где
- Расчетный %
- Общее кол-во открываний ячеек с расчетным %
- Кол-во попаданий на мину
- Фактический %
| 1. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2. | 31 | 55 | 117 | 131 | 304 | 291 | 303 | 339 | 507 | 435 | 479 | 1201 | 152 | 146 | 118 | 143 | 164 | 141 | 367 | 3968 | 145 | 63 | 47 | 26 | 92 |
| 3. | 1 | 4 | 9 | 6 | 20 | 19 | 27 | 29 | 56 | 43 | 60 | 147 | 15 | 25 | 14 | 20 | 33 | 26 | 65 | 350 | 14 | 5 | 12 | 4 | 23 |
| 4. | 3 | 7 | 7 | 4 | 6 | 6 | 8 | 8 | 11 | 9 | 12 | 12 | 9 | 17 | 11 | 13 | 20 | 18 | 17 | 8 | 9 | 7 | 25 | 15 | 25 |
| 1. | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2. | 18 | 10 | 24 | 18 | 9 | 11 | 6 | 135 | 8 | 2 | 4 | 2 | 1 | 3 | 16 | 2 | 2 | 1 | 462 | ||||||
| 3. | 1 | 9 | 2 | 3 | 3 | 2 | 1 | 43 | 1 | 0 | 1 | 0 | 0 | 1 | 4 | 1 | 1 | 0 | 210 | ||||||
| 4. | 5 | 37 | 11 | 30 | 33 | 18 | 16 | 31 | 12 | 0 | 25 | 0 | 0 | 33 | 25 | 50 | 50 | 0 | 45 |
Большое расхождение в области 20-22% вероятно связано с тем, что часто этот процент имели ячейки, не имеющие рядом уже открытые (например в начале игры), и «Сапер» подстраивался под игрока, иногда убирая из-под открываемой ячейки мину. Алгоритм работы был реализован на java и опробован на стандартном сапере Windows (7 и ХР), приложении в VK и на игруне. К слову сказать, после нескольких дней «технических неполадок» при доступе на мой аккаунт с моего IP игрун изменил правила вознаграждения за открытие части поля: изначально возвращал 10% ставки за 10% открытого поля, потом 5%, потом 2%, а когда я перестал играть, то вернул 5%.
