В настоящей статье мы продолжим рассмотрение проблемы компьютерных вычислений десятичных чисел с помощью двоичной арифметики, которая была затронута в предыдущем топике [1]. В статье речь пойдет об ошибках, которые в литературе принято называть ошибками округления. И, в частности, ошибок, которые порождаются в результате итерационного суммирования большого числа одинаковых десятичных чисел, представленных в двоичном виде ограниченным разрядным пространством. В результате исследований были получены простые рекуррентные соотношения, позволяющие точно определить ошибку компьютерных итерационных вычислений частичных сумм любого количества одинаковых слагаемых, на любом шаге итерации.
Будем рассматривать действительные положительные двоичные числа с фиксированным количеством L значащих цифр. Под фиксированным количеством L значащих цифр будем понимать L цифр, отсчет которых производится слева направо, начиная от старшей ненулевой цифры. Недостающее до L количество цифр в числе справа дополняется нулями. Так, если количество значащих цифр зафиксировать значением L=5, то число 0.0011 будет иметь следующие значащие цифры: 11000. Если теперь записать наше число в 5-разрядный компьютер, как число с плавающей точкой, то в область машинной мантиссы будет записано: .11000. Это число будет представлено в компьютере в нормализованном виде с экспонентой, равной 2^-2.
Число с плавающей точкой записывается в машинном слове, как произведение дробной мантиссы на экспоненту, порядок которой указывает на положение точки в числе, представленном в естественной форме. Если число цифр мантиссы числа не совпадает с количеством L разрядов машинной мантиссы, число нормализуют, сдвигая мантиссу в ту или иную сторону так, чтобы старшая ненулевая цифра числа располагалась в старшем разряде машинной мантиссы. При этом порядок экспоненты корректируют на число сдвигов.
Рассмотрим число в естественной форме. Если количество его значащих цифр превышает некоторое фиксированное количество L цифр, то оно должно быть преобразовано таким образом, чтобы количество его значащих цифр стало равно L. Это достигается путем отбрасывания лишних младших цифр. При отбрасывании младших цифр, число может быть округлено до L разрядов, или в нем просто усекаются лишние младшие цифры. Так, в случае усечения, двоичное число 10.0011, представленное в естественном виде, для L=5, будет записано как 10.001. То же число, записанное в экспоненциальном нормализованном виде, будет выглядеть как 0.10001*2^2. Здесь мы имеем две эквивалентные записи одного и того же числа.
Приведение числа, представленного в естественном виде, к числу с количеством значащих цифр L, будем называть оптимизацией. Мы вводим это понятие, чтобы отличать его от операции нормализации чисел, записанных в экспоненциальном виде. С математической точки зрения это две эквивалентные операции.
Далее будем рассматривать случай усечения младших цифр в двоичном числе без округления. Числа будем рассматривать представленными в естественном виде.
Пусть мы имеем некоторое число 2^p ≤Z < 2^(p+1), где p — целое число со знаком, равное расстоянию от разделительной точки до старшей ненулевой цифры в числе Z, записанном в естественном виде. Если старшая ненулевая цифра расположена слева от точки, то p > 0. Если цифра расположена справа от точки, то p < 0. Так, для числа Z=0.000101 будем иметь p = -4 и для этого случая: 2^(-4) ≤Z < 2^(-3).
Рассмотрим последовательность действительных двоичных чисел X0, X1,… Xi..., лежащих в интервалах:
2^p ≤ X0 < 2^(1+p) ≤ X1 < 2^(2+p);...; 2^(i+p) ≤ Xi < 2^(i+p+1)…
Например, для p=-3 мы будем иметь 2^p = 2^-3= 0.001. Наша последовательность тогда будет выглядеть как 0.001 ≤ X0 < 0.01 ≤ X1 < 0.1,...,2^( i -3) ≤ Xi < 2^( i -2)…
Возьмем некоторое действительное число 2^(i+p) ≤ Xi < 2^(i+p+1), имеющее ограниченное количество L значащих цифр. Возьмем далее сумму ki элементарных слагаемых: Z+Z+...= kiZ, где Z= X0, ki ≥ 0 — целое число. Выберем ki таким, чтобы 2^ (i+p) ≤ Xi+ kiZ < 2^( i+p +1). В этой сумме максимальное количество ki элементарных слагаемых Z, при котором значение суммы не превысит правую границу интервала, можно найти по формуле ki=⌊(2^(i+p+1)-Xi)/Z⌋, где скобки ⌊ ⌋ означают округление до ближайшего целого в меньшую сторону.
Если теперь к Xi+ kiZ прибавить еще одно элементарное слагаемое Z, получим Xi+1= Xi+ kiZ+Z= Xi+Z(ki+1) ≥ 2^( i+p +1). Значение вновь полученной суммы превысит или будет равно правому граничному значению интервала. Поэтому количество цифр в числе Xi+1= Xi+Z(ki+1) станет L+1. Чтобы выполнить требование равенства количества значащих цифр величине L, полученное число надо оптимизировать, т.е. привести к числу, в котором будет L значащих цифр. Для этого в нем надо отбросить младшую цифру. Операцию отбрасывания младшей цифры в числе Xi будем записывать как Xi ¬1. Например, если в числе X=10.0011 отбросить одну младшую цифру, то оно будет записано как X¬1=10.001. В общем случае, запись X¬t будет означать, что в числе X отброшено t младших разрядов.
После того, как на определенном итерационном шаге частичная сумма Xi+1=Xi+Z(ki+1) превысит значение 2^( i+p +1), которое мы будем называть правым граничным значением, старшая ненулевая цифра суммы окажется смещенной относительно фиксированной точки влево. Общее количество значащих цифр превысит число L на единицу и результат должен быть оптимизирован. Поскольку на i-м шаге итерации в результате оптимизации, в числе Xi младшая цифра отбрасывается, то число становится равным Xi¬1, тогда младшая цифра в слагаемом Z также может быть отброшена, т.к. на дальнейшие вычисления она влиять не будет.
Например. Пусть L=5. Найдем сумму двух чисел X =1.10111 и Z=0.10011. Т.к. количество цифр в X превышает величину L, оно должно быть оптимизировано. После оптимизации получим: X¬1=1.1011. Прибавим к этому числу Z=0.1001**1**. Получим X¬1+ Z =1.1011+0.1001**1**=10.0100**1**. Здесь количество цифр после запятой в слагаемом X¬1 меньше количества цифр в слагаемом Z. Поэтому младшая цифра в Z, помеченная жирным шрифтом, с одной стороны, всегда складывается с нулем, а с другой, результат сложения младших цифр в этом случае оказывается вне диапазона L значащих цифр и, следовательно, при усечении, не влияет на общую сумму. Отсюда следует, что сумма не изменится, если ее записать как X¬1+ Z¬1=1.1011+0.1001=10.0100. Поскольку в этой сумме количество цифр превысило величину L, то полученное число также должно быть оптимизировано. Отбросив младшую цифру, мы получим оптимизированное число 10.010 с L=5 значащими цифрами.
Таким образом, значения частичных сумм Xi и Xi+1 отличаются максимум на kiэлементарных слагаемых. Количество значащих цифр частичных сумм, лежащих в интервале [Xi, Xi+1) равно L и поэтому их значения вычисляются без округлений и, соответственно, не вносят ошибок. Прибавление (ki+1)-ого слагаемого к частичной сумме приводит к превышению правого граничного значения или его равенству. Если частичная сумма на каком-то шаге итерации превышает правое граничное значение или равно ему, то количество значащих цифр в сумме становится равным L+1 и требуется оптимизация. После каждого превышения правого граничного значения, количество значащих цифр элементарных слагаемых Z, принимающих участие в образовании новых частичных сумм уменьшается на единицу и после i-го правого граничного значения элементарное слагаемое становится равным Z¬i.
Xi+1= (Xi+ (ki+1+1)Z¬i)¬1, X0=Z, i=0,1…
ki+1=⌊(2^(p+i)-Xi)/Z¬i⌋, p- целое число со знаком.
Номер шага итерации Ni+1, на котором частичная сумма Xi+1 превысила правое граничное значение можно определить по рекуррентному соотношению:
Ni+1=(ki+1+1)+Ni.
Рассмотрим теперь, какую ошибку мы получаем при итерационном суммировании десятичных действительных чисел, представленных в двоичном виде, в результате операции усечения.
Известно, что любое десятичное число X, представленное в двоичном виде, после усечения количества значащих цифр, может быть записано как X= B +g, где B- представление десятичного числа X в двоичном виде с ограниченным фиксированным количеством значащих цифр, g — абсолютная погрешность представления числа в результате усечения. Эта погрешность может быть определена как g = X-B, g ≥0. При суммировании i элементарных слагаемых эта ошибка накапливается и становится равной ig.
Однако, это не единственная ошибка, которая образуется при рекуррентном сложении одинаковых элементарных слагаемых. В результате округления или усечения, при рекуррентном вычислении частичных сумм, образуются также ошибки округления.
Выведенные нами рекуррентные соотношения позволяют на любом шаге итерации получить точные значения ошибки вычисления суммы элементарных слагаемых, имеющих одинаковые значения.
Рассмотрим для примера частичные суммы элементарных слагаемых Z = 0.0011101, для которых L =5. Для числа Z мы будем иметь p = 0.001. В Таблице 1 приведены результаты сложения 10 элементарных слагаемых для каждого шага итерации.
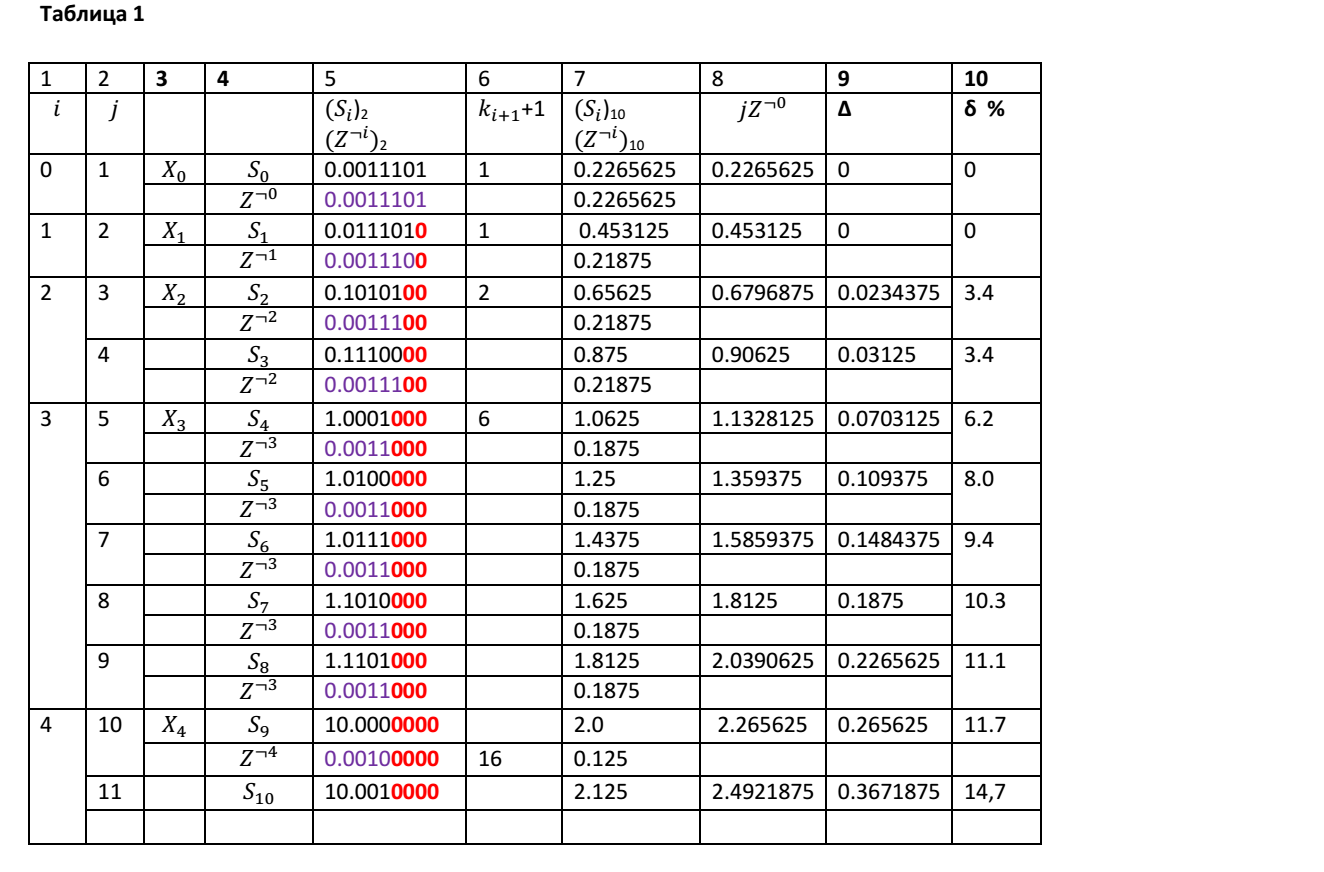
В столбце 1 таблицы представлены номера i частичных сумм Xi, которые превысили или стали равны правой границе интервала. Во втором столбце приведены номера итераций j. В столбце 3 приведены обозначения частичных сумм Xi при определенном значении i. В столбце 4 таблицы приведены друг под другом, соответственно, обозначения частичных сумм Sj и элементарных слагаемых Z¬i для каждого шага итерации. В столбце 5 приведены друг под другом, соответственно, значения частичных сумм Sj и элементарных слагаемых Z¬i для каждого шага итерации. Красным шрифтом отмечены разряды чисел, которые не принимают участие в образовании частичных сумм. В столбце 6 приведены значения коэффициентов ki+1+1, которые используются в нашей рекуррентной формуле для вычисления Xi+1. В столбце 7 приведены друг под другом, соответственно, значения частичных сумм Sj и элементарных слагаемых Z¬i для каждого шага итерации в десятичном виде. В столбце 8 приведены теоретические значения сумм элементарных слагаемых Z при условии, что погрешности округления не учитываются. В столбце 9 представлены значения абсолютных погрешностей вычисления на каждом шаге итерации, которые рассчитаны по формуле Δ=(Sj)10 — jZ¬0. В столбце 9 представлены значения относительных погрешностей, вычисляемых по формуле: δ= Δ/jZ¬0.
Как видно из приведенной таблицы, даже при условии, что элементарные слагаемые представлены точно, без погрешностей представления, в процессе итерационного суммирования очень быстро образуется такая величина погрешности, что вычисления на определенном шаге итерации становятся бессмысленными. Причина этой погрешности кроется в ограниченности машинного слова, а также в процедуре нормализации, или, в нашем случае, оптимизации представления чисел.
Ниже мы приводим Таблицу 2, в которой представлены значения частичных сумм при итерационном суммировании десятичного числа 0.1 в двоичном виде с фиксированным количеством значащих цифр, для 51 разрядной мантиссы. В таблице приведены значения частичных сумм в точках превышения правых граничных значений. Числа, выделенные жирным шрифтом в таблице, являются двоичными. Невыделенные жирным шрифтом числа, это числа, представленные в десятичном коде. В этой таблице приведены значения частичных сумм Xi, значения коэффициентов ki+1+1 для нахождения очередной частичной суммы Xi+1 в соответствие с нашими рекуррентными соотношениями.
Номер шага итерации Ni+1, на котором очередная частичная сумма превысила правое граничное значение можно определить по рекуррентному соотношению: Ni+1=(ki+1+1)+Ni.
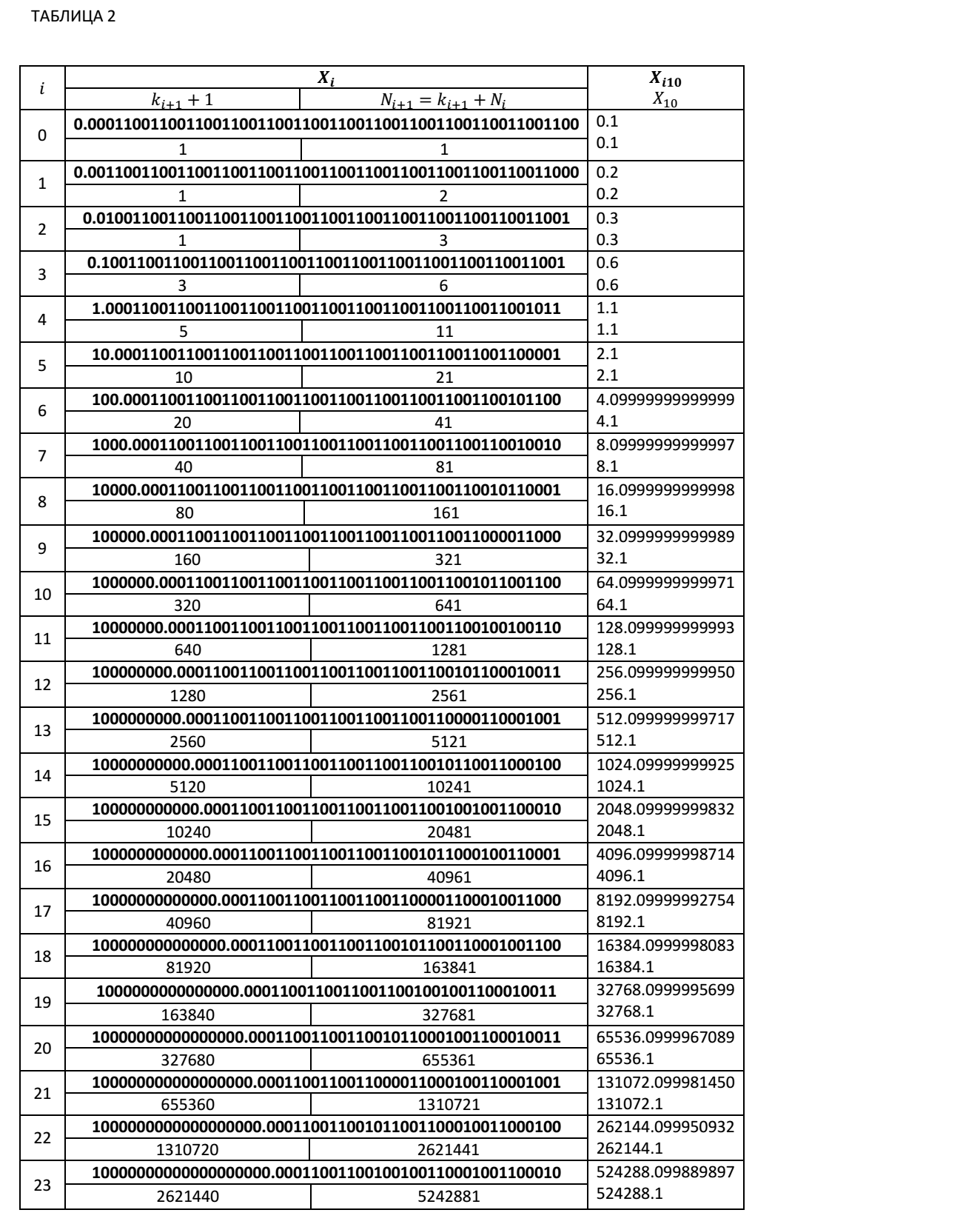
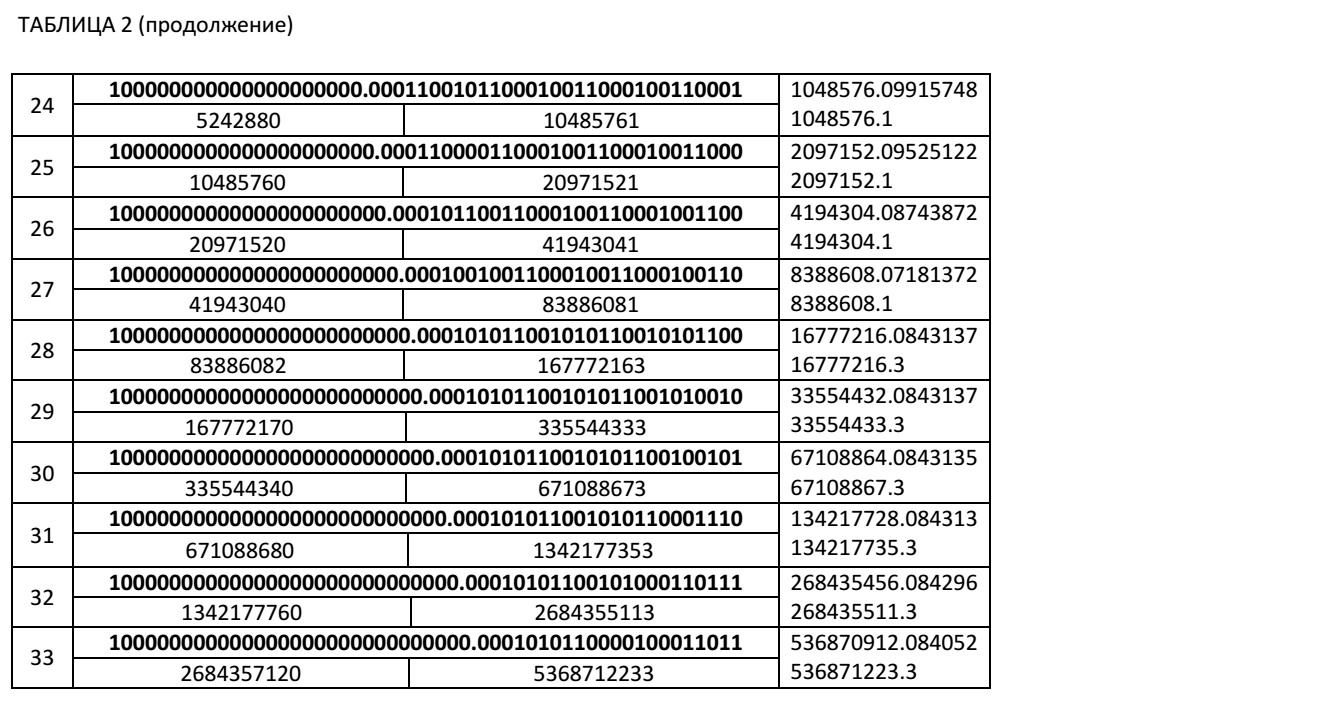
Как видно из Таблицы 2, при числе итераций 5368712233 уже в 6 знаке частичной суммы мы имеем неверную цифру. Абсолютная ошибка вычислений для этого случая составляет Δ= 536871223.3- 536870912.084052=311.215948. А относительная ошибка будет равна δ=311.215948/536871223.3≈0.0000006=0.00006%.
В то же время, если вычислить погрешность представления десятичного числа 0.1 в двоичном виде с 51 значащей цифрой, то мы будем иметь: 0.1=0.0001100110011001100110011001100110011001100110011001100≈ 0.09999999999999997779
Δ=0.1-0.09999999999999997779≈2.221*10^(-17),
δ=2.221*10^(-17)/0.1=2.221*10^(-16)=14*10^(-14)%.
На шаге итерации, равном 5368712233, суммарная абсолютная погрешность представления принимает значение 5368712233*14*10^(-18)≈ 0.000000075. Относительная же погрешность представления не меняется при любом шаге итерации.
Как мы видим, абсолютная погрешность представления оказывается ничтожно малой по сравнению с погрешностью округления при итерационном суммировании.
Представленные нами здесь рекуррентные формулы позволили получить точные расчетные погрешности округления при итерационном суммировании большого числа одинаковых десятичных слагаемых, представленных в двоичном коде.
Автор благодарит пользователя mayorovp за обнаруженные неточности.
ЛИТЕРАТУРА
1. habrahabr.ru/post/309812
Будем рассматривать действительные положительные двоичные числа с фиксированным количеством L значащих цифр. Под фиксированным количеством L значащих цифр будем понимать L цифр, отсчет которых производится слева направо, начиная от старшей ненулевой цифры. Недостающее до L количество цифр в числе справа дополняется нулями. Так, если количество значащих цифр зафиксировать значением L=5, то число 0.0011 будет иметь следующие значащие цифры: 11000. Если теперь записать наше число в 5-разрядный компьютер, как число с плавающей точкой, то в область машинной мантиссы будет записано: .11000. Это число будет представлено в компьютере в нормализованном виде с экспонентой, равной 2^-2.
Число с плавающей точкой записывается в машинном слове, как произведение дробной мантиссы на экспоненту, порядок которой указывает на положение точки в числе, представленном в естественной форме. Если число цифр мантиссы числа не совпадает с количеством L разрядов машинной мантиссы, число нормализуют, сдвигая мантиссу в ту или иную сторону так, чтобы старшая ненулевая цифра числа располагалась в старшем разряде машинной мантиссы. При этом порядок экспоненты корректируют на число сдвигов.
Рассмотрим число в естественной форме. Если количество его значащих цифр превышает некоторое фиксированное количество L цифр, то оно должно быть преобразовано таким образом, чтобы количество его значащих цифр стало равно L. Это достигается путем отбрасывания лишних младших цифр. При отбрасывании младших цифр, число может быть округлено до L разрядов, или в нем просто усекаются лишние младшие цифры. Так, в случае усечения, двоичное число 10.0011, представленное в естественном виде, для L=5, будет записано как 10.001. То же число, записанное в экспоненциальном нормализованном виде, будет выглядеть как 0.10001*2^2. Здесь мы имеем две эквивалентные записи одного и того же числа.
Приведение числа, представленного в естественном виде, к числу с количеством значащих цифр L, будем называть оптимизацией. Мы вводим это понятие, чтобы отличать его от операции нормализации чисел, записанных в экспоненциальном виде. С математической точки зрения это две эквивалентные операции.
Далее будем рассматривать случай усечения младших цифр в двоичном числе без округления. Числа будем рассматривать представленными в естественном виде.
Пусть мы имеем некоторое число 2^p ≤Z < 2^(p+1), где p — целое число со знаком, равное расстоянию от разделительной точки до старшей ненулевой цифры в числе Z, записанном в естественном виде. Если старшая ненулевая цифра расположена слева от точки, то p > 0. Если цифра расположена справа от точки, то p < 0. Так, для числа Z=0.000101 будем иметь p = -4 и для этого случая: 2^(-4) ≤Z < 2^(-3).
Рассмотрим последовательность действительных двоичных чисел X0, X1,… Xi..., лежащих в интервалах:
2^p ≤ X0 < 2^(1+p) ≤ X1 < 2^(2+p);...; 2^(i+p) ≤ Xi < 2^(i+p+1)…
Например, для p=-3 мы будем иметь 2^p = 2^-3= 0.001. Наша последовательность тогда будет выглядеть как 0.001 ≤ X0 < 0.01 ≤ X1 < 0.1,...,2^( i -3) ≤ Xi < 2^( i -2)…
Возьмем некоторое действительное число 2^(i+p) ≤ Xi < 2^(i+p+1), имеющее ограниченное количество L значащих цифр. Возьмем далее сумму ki элементарных слагаемых: Z+Z+...= kiZ, где Z= X0, ki ≥ 0 — целое число. Выберем ki таким, чтобы 2^ (i+p) ≤ Xi+ kiZ < 2^( i+p +1). В этой сумме максимальное количество ki элементарных слагаемых Z, при котором значение суммы не превысит правую границу интервала, можно найти по формуле ki=⌊(2^(i+p+1)-Xi)/Z⌋, где скобки ⌊ ⌋ означают округление до ближайшего целого в меньшую сторону.
Если теперь к Xi+ kiZ прибавить еще одно элементарное слагаемое Z, получим Xi+1= Xi+ kiZ+Z= Xi+Z(ki+1) ≥ 2^( i+p +1). Значение вновь полученной суммы превысит или будет равно правому граничному значению интервала. Поэтому количество цифр в числе Xi+1= Xi+Z(ki+1) станет L+1. Чтобы выполнить требование равенства количества значащих цифр величине L, полученное число надо оптимизировать, т.е. привести к числу, в котором будет L значащих цифр. Для этого в нем надо отбросить младшую цифру. Операцию отбрасывания младшей цифры в числе Xi будем записывать как Xi ¬1. Например, если в числе X=10.0011 отбросить одну младшую цифру, то оно будет записано как X¬1=10.001. В общем случае, запись X¬t будет означать, что в числе X отброшено t младших разрядов.
После того, как на определенном итерационном шаге частичная сумма Xi+1=Xi+Z(ki+1) превысит значение 2^( i+p +1), которое мы будем называть правым граничным значением, старшая ненулевая цифра суммы окажется смещенной относительно фиксированной точки влево. Общее количество значащих цифр превысит число L на единицу и результат должен быть оптимизирован. Поскольку на i-м шаге итерации в результате оптимизации, в числе Xi младшая цифра отбрасывается, то число становится равным Xi¬1, тогда младшая цифра в слагаемом Z также может быть отброшена, т.к. на дальнейшие вычисления она влиять не будет.
Например. Пусть L=5. Найдем сумму двух чисел X =1.10111 и Z=0.10011. Т.к. количество цифр в X превышает величину L, оно должно быть оптимизировано. После оптимизации получим: X¬1=1.1011. Прибавим к этому числу Z=0.1001**1**. Получим X¬1+ Z =1.1011+0.1001**1**=10.0100**1**. Здесь количество цифр после запятой в слагаемом X¬1 меньше количества цифр в слагаемом Z. Поэтому младшая цифра в Z, помеченная жирным шрифтом, с одной стороны, всегда складывается с нулем, а с другой, результат сложения младших цифр в этом случае оказывается вне диапазона L значащих цифр и, следовательно, при усечении, не влияет на общую сумму. Отсюда следует, что сумма не изменится, если ее записать как X¬1+ Z¬1=1.1011+0.1001=10.0100. Поскольку в этой сумме количество цифр превысило величину L, то полученное число также должно быть оптимизировано. Отбросив младшую цифру, мы получим оптимизированное число 10.010 с L=5 значащими цифрами.
Таким образом, значения частичных сумм Xi и Xi+1 отличаются максимум на kiэлементарных слагаемых. Количество значащих цифр частичных сумм, лежащих в интервале [Xi, Xi+1) равно L и поэтому их значения вычисляются без округлений и, соответственно, не вносят ошибок. Прибавление (ki+1)-ого слагаемого к частичной сумме приводит к превышению правого граничного значения или его равенству. Если частичная сумма на каком-то шаге итерации превышает правое граничное значение или равно ему, то количество значащих цифр в сумме становится равным L+1 и требуется оптимизация. После каждого превышения правого граничного значения, количество значащих цифр элементарных слагаемых Z, принимающих участие в образовании новых частичных сумм уменьшается на единицу и после i-го правого граничного значения элементарное слагаемое становится равным Z¬i.
Xi+1= (Xi+ (ki+1+1)Z¬i)¬1, X0=Z, i=0,1…
ki+1=⌊(2^(p+i)-Xi)/Z¬i⌋, p- целое число со знаком.
Номер шага итерации Ni+1, на котором частичная сумма Xi+1 превысила правое граничное значение можно определить по рекуррентному соотношению:
Ni+1=(ki+1+1)+Ni.
Рассмотрим теперь, какую ошибку мы получаем при итерационном суммировании десятичных действительных чисел, представленных в двоичном виде, в результате операции усечения.
Известно, что любое десятичное число X, представленное в двоичном виде, после усечения количества значащих цифр, может быть записано как X= B +g, где B- представление десятичного числа X в двоичном виде с ограниченным фиксированным количеством значащих цифр, g — абсолютная погрешность представления числа в результате усечения. Эта погрешность может быть определена как g = X-B, g ≥0. При суммировании i элементарных слагаемых эта ошибка накапливается и становится равной ig.
Однако, это не единственная ошибка, которая образуется при рекуррентном сложении одинаковых элементарных слагаемых. В результате округления или усечения, при рекуррентном вычислении частичных сумм, образуются также ошибки округления.
Выведенные нами рекуррентные соотношения позволяют на любом шаге итерации получить точные значения ошибки вычисления суммы элементарных слагаемых, имеющих одинаковые значения.
Рассмотрим для примера частичные суммы элементарных слагаемых Z = 0.0011101, для которых L =5. Для числа Z мы будем иметь p = 0.001. В Таблице 1 приведены результаты сложения 10 элементарных слагаемых для каждого шага итерации.

В столбце 1 таблицы представлены номера i частичных сумм Xi, которые превысили или стали равны правой границе интервала. Во втором столбце приведены номера итераций j. В столбце 3 приведены обозначения частичных сумм Xi при определенном значении i. В столбце 4 таблицы приведены друг под другом, соответственно, обозначения частичных сумм Sj и элементарных слагаемых Z¬i для каждого шага итерации. В столбце 5 приведены друг под другом, соответственно, значения частичных сумм Sj и элементарных слагаемых Z¬i для каждого шага итерации. Красным шрифтом отмечены разряды чисел, которые не принимают участие в образовании частичных сумм. В столбце 6 приведены значения коэффициентов ki+1+1, которые используются в нашей рекуррентной формуле для вычисления Xi+1. В столбце 7 приведены друг под другом, соответственно, значения частичных сумм Sj и элементарных слагаемых Z¬i для каждого шага итерации в десятичном виде. В столбце 8 приведены теоретические значения сумм элементарных слагаемых Z при условии, что погрешности округления не учитываются. В столбце 9 представлены значения абсолютных погрешностей вычисления на каждом шаге итерации, которые рассчитаны по формуле Δ=(Sj)10 — jZ¬0. В столбце 9 представлены значения относительных погрешностей, вычисляемых по формуле: δ= Δ/jZ¬0.
Как видно из приведенной таблицы, даже при условии, что элементарные слагаемые представлены точно, без погрешностей представления, в процессе итерационного суммирования очень быстро образуется такая величина погрешности, что вычисления на определенном шаге итерации становятся бессмысленными. Причина этой погрешности кроется в ограниченности машинного слова, а также в процедуре нормализации, или, в нашем случае, оптимизации представления чисел.
Ниже мы приводим Таблицу 2, в которой представлены значения частичных сумм при итерационном суммировании десятичного числа 0.1 в двоичном виде с фиксированным количеством значащих цифр, для 51 разрядной мантиссы. В таблице приведены значения частичных сумм в точках превышения правых граничных значений. Числа, выделенные жирным шрифтом в таблице, являются двоичными. Невыделенные жирным шрифтом числа, это числа, представленные в десятичном коде. В этой таблице приведены значения частичных сумм Xi, значения коэффициентов ki+1+1 для нахождения очередной частичной суммы Xi+1 в соответствие с нашими рекуррентными соотношениями.
Номер шага итерации Ni+1, на котором очередная частичная сумма превысила правое граничное значение можно определить по рекуррентному соотношению: Ni+1=(ki+1+1)+Ni.


Как видно из Таблицы 2, при числе итераций 5368712233 уже в 6 знаке частичной суммы мы имеем неверную цифру. Абсолютная ошибка вычислений для этого случая составляет Δ= 536871223.3- 536870912.084052=311.215948. А относительная ошибка будет равна δ=311.215948/536871223.3≈0.0000006=0.00006%.
В то же время, если вычислить погрешность представления десятичного числа 0.1 в двоичном виде с 51 значащей цифрой, то мы будем иметь: 0.1=0.0001100110011001100110011001100110011001100110011001100≈ 0.09999999999999997779
Δ=0.1-0.09999999999999997779≈2.221*10^(-17),
δ=2.221*10^(-17)/0.1=2.221*10^(-16)=14*10^(-14)%.
На шаге итерации, равном 5368712233, суммарная абсолютная погрешность представления принимает значение 5368712233*14*10^(-18)≈ 0.000000075. Относительная же погрешность представления не меняется при любом шаге итерации.
Как мы видим, абсолютная погрешность представления оказывается ничтожно малой по сравнению с погрешностью округления при итерационном суммировании.
Представленные нами здесь рекуррентные формулы позволили получить точные расчетные погрешности округления при итерационном суммировании большого числа одинаковых десятичных слагаемых, представленных в двоичном коде.
Автор благодарит пользователя mayorovp за обнаруженные неточности.
ЛИТЕРАТУРА
1. habrahabr.ru/post/309812
