Комментарии 22
Японская свеча неинтуитивнаа и не логична. Лучше тут подходит такая диаграмма: вертикальная линия показывает разброс, ус влево показывает начальное значение, ус вправо — конечное.
Очень люблю boxplot использовать при визуализации лабораторных данных. Очень компактно. Если еще и цвет делать значимым, то плотность информации вообще дикая.
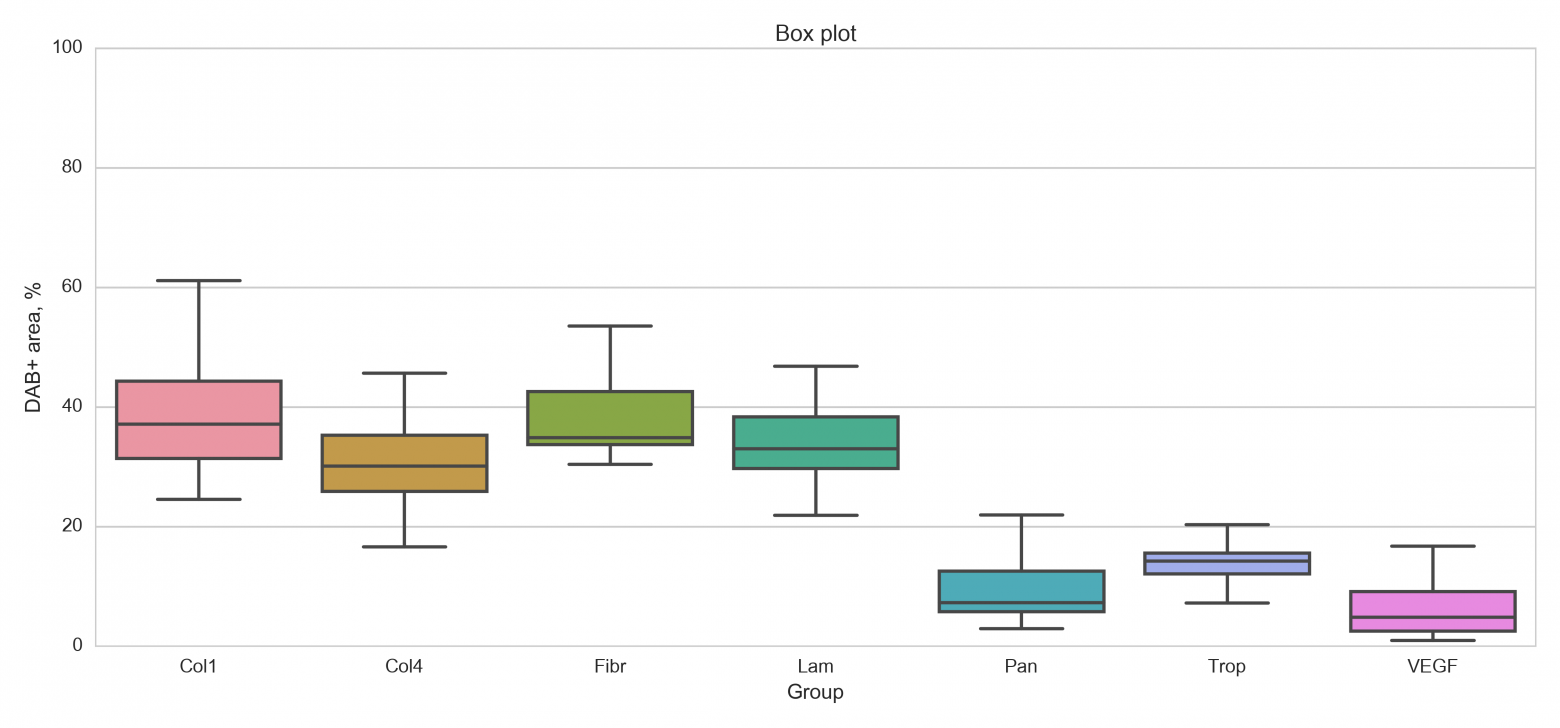
Еще очень удобны засечки (notches), обозначающие доверительный интервал медианы. Можно быстро и довольно надежно судить о значимости различий между группами наблюдений.

Примечание: TSR = Total Support Ratio — отношение численности населения в трудоспособном возрасте (15-64) к численности населения старше моложе трудоспособного возраста
Krzywinski, M., & Altman, N. (2014). Points of Significance: Visualizing samples with box plots. Nature Methods, 11(2), 119–120. https://doi.org/10.1038/nmeth.2813
McGill, R., Tukey, J. W., & Larsen, W. A. (1978). Variations of Box Plots. The American Statistician, 32(1), 12–16. https://doi.org/10.2307/2683468
Что-то я не уловил отличий от boxplot.
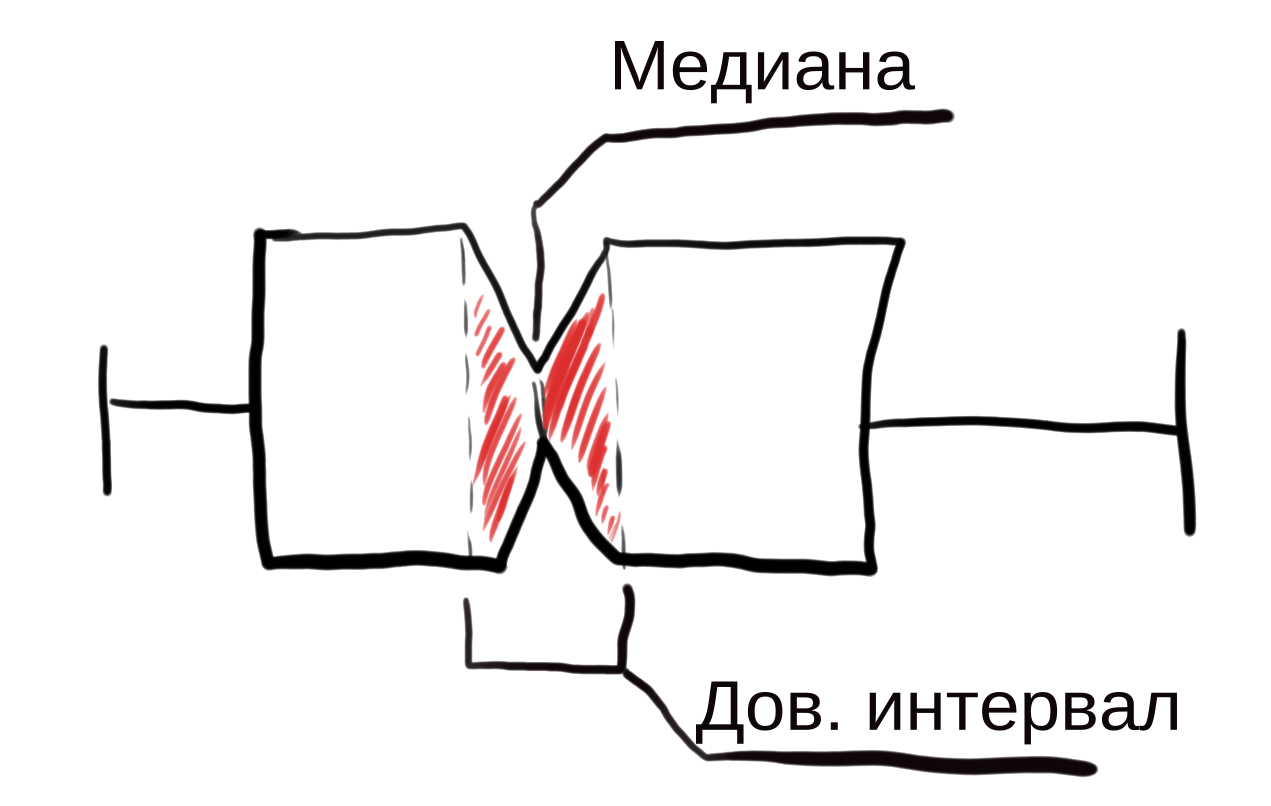
Я правильно понял обозначение?
да
Но это довольно грубый и быстрый способ расчета доверительного интервала

Ух. Красота. Жаль Seaborn не поддерживает. Надо feature request написать им. А почему грубо? И доверительный интервал для какой вероятности?
UPD: Увидел, что для 95%
Да, это очень мощное дополнение к боксплоту.
Ну а грубо по многим причинам. Главное (насколько я понимаю): мы визуализируем распределения с помощью боксплота, как правило, перед тем, как покрутить регрессии и посмотреть значимость различий. В большинстве случаев результаты анализа говорят нам о различиях в средних значениях, а не медианных. То есть аналитическая мощь этих засечек опирается на допущение о нормальности распределения, что редко бывает совсем уж правдой. Но все это значимо лишь в пограничных случаях (когда, кстати, и выбор 95% доверительного интервала — не более чем условность). Если различия по засечкам большие, то можно быть уверенным в их статистической значимости.
Вот варианты маскимальной плотности сжатия информации с помощью библиотеки seaborn.
Boxplot:
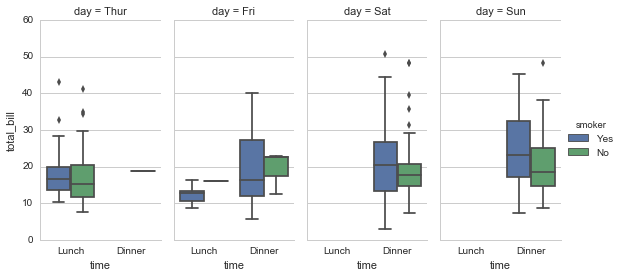
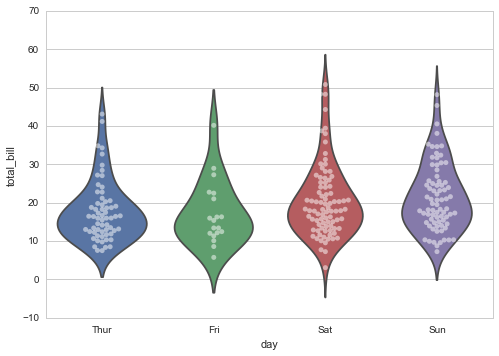
Violinplot — показывает гистограмму распределения одновременно с медианой и прочими вещами:
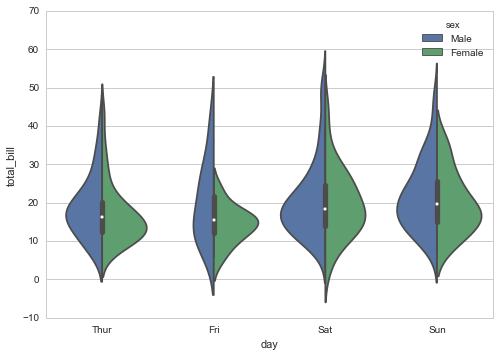
А еще мне очень нравится swarmplot для категорийных данных:
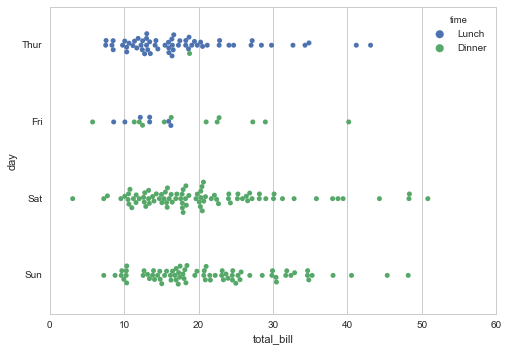
Или комбинация с другими вариантами одновременно:
Всегда думал что размерность определяется по количеству осей. У Вас на всех графиках две оси — почему вы считаете данные одномерными? Как по вашему выглядит трехмерный график?
Размерность — количество независимых параметров, необходимое и достаточное, чтобы задать местоположение в пространстве.
Пространство трактуется максимально широко. Например, это может быть пространство решений о погоде на улице. Обычно мы используем два параметра, выходя из дома: температуру и наличие осадков. То есть, пространство двумерно. Добавим скорость ветра — пространство станет трехмерным. И т.д.
Земля шарообразная, то есть, явно трехмерная. Однако, мы спокойно обходимся двумя параметрами для ориентирования — широтой и долготой. Благодаря этому возможны и благополучно используются уже тысячелетия плоские (двумерные) географические карты.
Карты же (физические) и являются одним из возможных вариантов трехмерного графика. Третий параметр — высота над уровнем моря — изображается цветом.
Другой вариант трехмерного графика — пузырьковая диаграмма. Но этот вариант уже не такой эффектный. Если пузырьков, отвечающих за третье измерение, становится много, то график перестает читаться.
Еще один важный момент, который имеет уже непосредственное отношение к графикам и осям, это зависимость переменных. В размерности учитывается независимость параметров. То есть, когда нельзя рассчитать один параметр на основании другого. Например, широта никак не зависит от долготы и наоборот. Кстати, с погодой уже не все так однозначно, но в общем случае и тепло, и холод могут сопровождаться или нет дождем.
Если мы рисуем график некоей функции y=f(x), то y — это зависимая переменная, а x — нет. Зная x, мы можем определить y (местоположение). Поэтому данные одномерные. Однако, осей у нас две, потому что мы пользуемся двумерной визуализацией. Размерность визуализации специально «избыточна» для наглядности. В данном случае, x просто задает диапазон, в котором мы смотрим значения y.
И, наконец, про графики, которые с двумя осями, но я называю одномерными. На них вторая размерность визуализации как бы схлопывается, и мы смотрим только на одну:
— свеча: мы отбросили протяженность во времени. На весь график мы смотрим как на один момент времени и характеризуем его несколькими значениями исходной переменной.
— круговая диаграмма: на ней значимой является только доля, изображаемая углом. Посмотрите на это как на полярные координаты, в которых мы не пользуемся радиусом. Угол однозначно определяет местоположение на окружности. В этом смысле окружность одномерна.
— боксплот: тут схлопывается все частотное разнообразие распределения. Мы просто помечаем отрезком на числовой оси место наиболее вероятного нахождения наших значений. Сколько их там на самом деле и как они распределены, боксплот уже не показывает, по сравнению с гистограммой.
если говорить по «плоские» графики — то они не зря называются «2D» имеется ввиду все же 2 измерения.
к ним добавляют еще размер и цвет — получаем «bubble chart» — на плоскости визуализация 4-х независымых переменных
круговая диаграмма — да она одномерна, еще есть например timeline и пр.
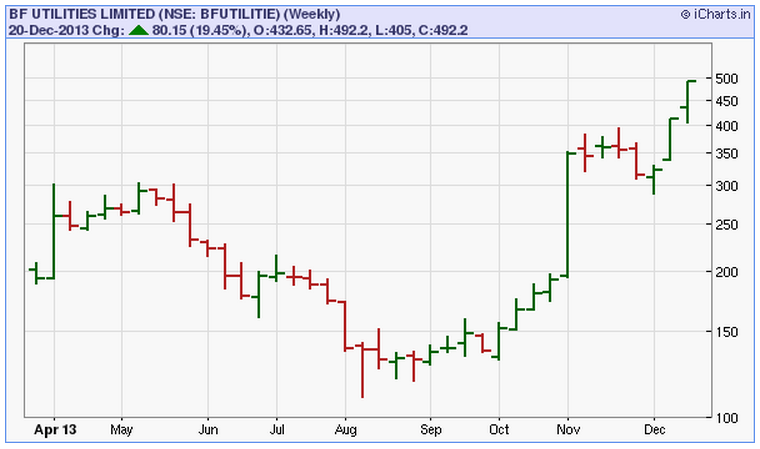

Выбор диаграммы для одномерных данных: геометрическая модель