Фильтр анизотропной диффузии Перона и Малика — это сглаживающий цифровые изображения фильтр, ключевая особенность которого состоит в том, что при сглаживании он сохраняет и «усиливает» границы областей на изображении.
В статье я кратко рассмотрю зачем нужен этот фильтр, теорию по нему и как его реализовать алгоритмически, приведу код на языке Fortran и примеры сглаженных изображений.

Крайнее левое изображение — оригинальное, справа от оригинального — фильтрованные с различными параметрами.
В обработке изображений (особенно в машинном зрении) не редко встают задачи сегментации или выделения границ областей. Но если изображение получается как результат обработки информации с некоторого физического устройства как фотоаппарат, томограф и т.д., то оно обычно зашумлено, причем природа шумов на изображении может быть разная — как вызванная физическими явлениями, так и различными алгоритмическими и аппаратными особенностями.
Шумы сильно усложняют задачи сегментации и выделения границ, поэтому, обычно, такие изображение сперва пропускают через некоторые сглаживающие фильтры, которые помимо сглаживания шумов, сглаживают и все остальное, что хорошо для той же сегментации, ведь несущественных деталей становится меньше. Изображение, если рассматри��ать его как функцию двух переменных, становится более гладким, что существенно облегчает выделение областей на нем.
Тем не менее, при использовании таких фильтров мы еще и сглаживаем границы областей внутри изображения. То есть, чем сильнее сглаживание, тем больше мы отходим от изначальных границ. В некоторых задачах это может быть допустимо, но, например, в медицине, в автоматической сегментации снимков томографии различных частей человеческого тела, важно сохранить изначальные границы областей (здесь в роли областей выступают внутренние органы, их деформации, различные опухоли и т.д.).
Формального математически строго определения границы области для произвольного изображения не существует (это бы решило очень много проблем в теории обработки изображений).
Впервые был описан в статье указанных математиков в 1990 году (ссылка на статью приведена в «источниках» в конце поста). Не будем вдаваться в глубокие теоретические детали, а хотя бы поверхностно рассмотрим как работает фильтр.
Здесь и далее рассматриваются изображения в градациях серого. Для цветных можно проводить сглаживания по каждому каналу независимо.
Итак, в фильтре анизотропной диффузии сглаженное изображение представляет собой некоторый член семейства изображений, полученных решением следующего уравнения математической физики:
C начальным условием:
Где:
 — однопараметрическое семейство изображений; чем больше
— однопараметрическое семейство изображений; чем больше  , тем больше степень размытия исходного изображения;
, тем больше степень размытия исходного изображения;
 — исходное изображение;
— исходное изображение;
 — производная по
— производная по  ;
;
 — оператор дивергенции;
— оператор дивергенции;
 — градиент;
— градиент;
С точки зрения теории, изображение — это некоторая непрерывная функция двух переменных, а сама картинка (матрица пикселей) — дискретизация этой функции. Причем 0 соответствует нулевой яркости точки изображения, то есть обозначает черный цвет.
По своей сути фильтр анизотропной диффузии является модификацией фильтра Гаусса.
Если подставить вместо, пока еще не рассмотренной, функции единицу, то есть
единицу, то есть  , то получается уравнени�� изотропной диффузии:
, то получается уравнени�� изотропной диффузии:
Математики Коендеринк и Гумел показали, что такое семейство размытых изображений по параметру , можно эквивалентно получить как решение уравнения свертки функции изображения с ядром Гаусса (это и есть фильтр Гаусса):
, можно эквивалентно получить как решение уравнения свертки функции изображения с ядром Гаусса (это и есть фильтр Гаусса):
Где:
 — оператор свертки;
— оператор свертки;
 — функция ядра Гаусса c нулевым математическим ожиданием и
— функция ядра Гаусса c нулевым математическим ожиданием и  среднеквадратичным отклонением;
среднеквадратичным отклонением;
Очевидно, функция играет роль некоторого «регулировщика» сглаживания.
играет роль некоторого «регулировщика» сглаживания.
Исходя из уравнения фильтра (1), для сохранения изначального значения в точке изображения нужно, чтобы производная по времени равнялась нулю (то есть значение на любых слоях размытия было константой). Получаем следующие условия на функцию :
:
 — на границах;
— на границах;
 — внутри областей, иначе говоря, внутри областей должно происходить обычное гауссово размытие;
— внутри областей, иначе говоря, внутри областей должно происходить обычное гауссово размытие;
Перона и Малик использовали градиент функции изображения как простую для расчета и достаточно точную аппроксимацию границ областей. Чем больше норма градиента, тем четче граница. Исходя из этого получаем:
как простую для расчета и достаточно точную аппроксимацию границ областей. Чем больше норма градиента, тем четче граница. Исходя из этого получаем:
Где — некоторая функция с област��ю значений на отрезке
— некоторая функция с област��ю значений на отрезке ![$[0;1]$](https://habrastorage.org/getpro/habr/formulas/2b1/73e/529/2b173e5293c3837d17126c9bfe1b2d71.svg) .
.
Из-за нечеткого определения границ через норму градиента, требуют также, чтобы функция была монотонной убывающей.
была монотонной убывающей.
Перона и Малик предложили два варианта функции :
:
Где — параметр, определяемый либо опытным путем, либо некоторым «измерителем» зашумленности.
— параметр, определяемый либо опытным путем, либо некоторым «измерителем» зашумленности.
Рассмотрим детальнее вторую функцию (формула 3). Для этого построим графики функции для нескольких разных
для нескольких разных  .
.
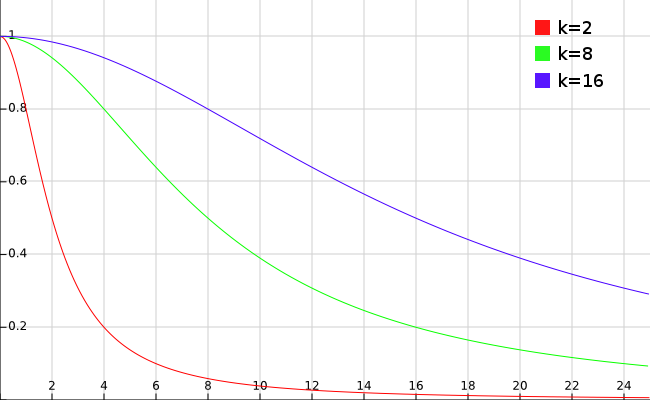
Видно, что чем больше , тем больше значение функции
, тем больше значение функции  для любой фиксированной точки.
для любой фиксированной точки.
Например, пусть в некоторой точке изображения, назовем ее , мы знаем значение нормы градиента на уровне
, мы знаем значение нормы градиента на уровне  :
:  . Тогда
. Тогда  , в то время как
, в то время как  . Получается в первом случае мы слабо «сгладили» значение в точке, так как по введенному ранее критерию она скорее всего лежит на границе, а во втором — значение функции
. Получается в первом случае мы слабо «сгладили» значение в точке, так как по введенному ранее критерию она скорее всего лежит на границе, а во втором — значение функции  практически единица, соответственно точка не считается граничной и будет сглажена обычным гауссовым размытием.
практически единица, соответственно точка не считается граничной и будет сглажена обычным гауссовым размытием.
Таким образом, выступает в роли «барьера» для шумов, и с возрастанием
выступает в роли «барьера» для шумов, и с возрастанием  возрастает «требование» на то, что точка будет считаться граничной.
возрастает «требование» на то, что точка будет считаться граничной.
Для того чтобы перейти непосредственно к алгоритму фильтра, произведем дискретизацию уравнения. Достаточно простой с точки зрения математических выкладок и нетребовательной к вычислениям будет дискретизация уравнения методом конечных разностей. Для удобства перепишем основное уравнение:
Теперь запишем конечно-разностную явную схему:
![$ I(x,y,t+\Delta t)-I(x,y,t)=\\ \hspace{55mm}=\frac{\Delta t}{(\Delta x)^{2}}\left [ c(x+\frac{\Delta x}{2},y,t)\cdot (I(x+\Delta x,y,t)-I(x,y,t))-\\ \hspace{68mm}-c(x-\frac{\Delta x}{2},y,t)\cdot (I(x,y,t)-I(x-\Delta x,y,t))\right ]+\\ \hspace{55mm}+\frac{\Delta t}{(\Delta y)^{2}}\left [ c(x,y+\frac{\Delta y}{2},t)\cdot (I(x,y+\Delta y,t)-I(x,y,t))-\\ \hspace{68mm}-c(x,y-\frac{\Delta y}{2},t)\cdot (I(x,y,t)-I(x,y-\Delta y,t))\right ]$](https://habrastorage.org/getpro/habr/formulas/2e4/6d0/d07/2e46d0d0761657114ef91db66a2493a3.svg)
Записать условие устойчивости для получившейся явной схемы — нетривиальная задача из-за нелинейности уравнения. Но Перона и Малик определили, что при схема будет устойчива для всех
схема будет устойчива для всех  . Учитывая этот факт и то, что дискретным представлением функции изображения будет матрица значений пикселей, перепишем основную расчетную схему в матричном виде:
. Учитывая этот факт и то, что дискретным представлением функции изображения будет матрица значений пикселей, перепишем основную расчетную схему в матричном виде:
Где:








Для расчета коэффициентов вначале необходимо вычислить норму градиента. Самый простой способ аппроксимировать норму градиента — это заменить ее на длину проекции градиента на соответствующую ось разностной сетки.
вначале необходимо вычислить норму градиента. Самый простой способ аппроксимировать норму градиента — это заменить ее на длину проекции градиента на соответствующую ось разностной сетки.




Хотя это достаточна грубая замена, аппроксимирующая несколько другое уравнение диффузии, она тем не менее также обеспечивает сохранение общей яркости изображения, а также дает практически идентичные результаты в сравнении с более точной аппроксимацией нормы градиента, выигрывая у последней в скорости вычислений.
Окончательно расчетная формула будет выглядеть так:
Где:




Схематично расчетную схему можно изобразить как на рисунке ниже.
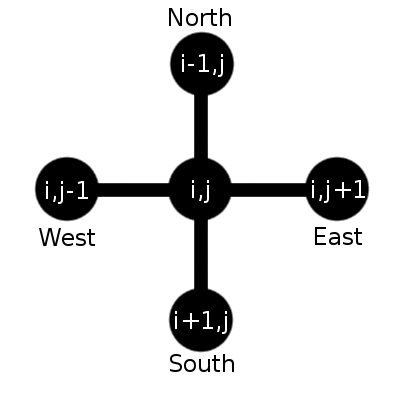
То есть новое значение зависит от текущего значения и значений четырех соседей ячейки матрицы. Возникает вопрос — как пересчитывать граничные ячейки, ведь расчетная схема в таком случае будет выходить за пределы матрицы.

Чтобы фильтр менял значения яркости в ячейках в рамках максимума и минимума яркости исходного изображения, процесс, описанный основным уравнением, должен быть адиабатическим. Отсюда имеем граничное условие Дирихле вида: . То есть просто заполняем границы нулями.
. То есть просто заполняем границы нулями.
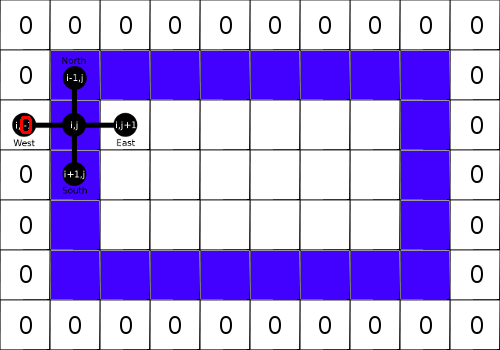
Исходя из расчетной формулы в памяти всегда придется держать как минимум два двумерных массива, первый будет соответствовать оригинальному изображению, второй — размытому. Если провести аналогию с фильтром Гаусса, то для размытия изображения с радиусом в фильтре Перона и Малика нам нужно выполнить
в фильтре Перона и Малика нам нужно выполнить  повторений полного пересчета изображения, каждый раз заменяя изображение с предыдущего слоя размытия на «оригинальное».
повторений полного пересчета изображения, каждый раз заменяя изображение с предыдущего слоя размытия на «оригинальное».
Последовательность действий будет примерно такая:
Для цветных изображений принцип действий сохраняется, но пересчет нужно выполнять для каждого канала отдельно.
На самом деле алгоритм достаточно тривиальный и легко может быть запрограммирован на многих популярных языках. Я в свое время столкнулся с трудностью реализации на фортране, так как долгое время не мог найти хорошего мануала или учебника по языку. Поэтому хочу привести реализацию именно на этом языке, в надежде, что кому-нибудь это пригодится.
Как ни странно, основная трудность при программировании заключалась в считывании картинки. В фортране отсутствуют встроенные процедуру (в языке их называют «сабрутинами») для манипуляций с изображениями, но есть все, что нужно для реализации своих процедур.
Самым простым форматом, который к тому же понимают и многие графические редакторы, мне показался PGM P5. Это открытый формат хранения растровых изображений типа bitmap без сжатия в оттенках серого. У него простой ASCII заголовок, а само изображение есть последовательность однобайтных (для оттенков серого от 0 до 255) целых чисел без знака. Подробнее о формате вы можете прочитать непосредственно в самом стандарте, ссылка приведена в разделе источников.
Я оформил процедуру для работы с PGM в виде модуля, подробно разбирать его не буду, так как это не относится к основной теме, приведу только ссылку на исходный код. Данный модуль работает только с изображениями с максимальным значением серого в 255.
Начнем программу с подключения модуля для работы с PGM и объявления всех необходимых переменных.
Параметр
Теперь считаем размеры входного изображения в переменные
Выделим память для массива изображения и массива сглаженного изображения и считаем в первый данные из файла
Фортран позволяет программисту самому определ��ть индекс первого элемента в массиве, поэтому, учитывая, что вокруг изображения должны быть нули, заранее заполняем матрицу u нулями, задав ей размер от
Процедура
Хотя в данном случае это неважно, хочу отметить, что изображение будет считано в транспонированном виде, так как фортран хранит двумерные массивы как последовательности столбцов, а формат PGM хранит изображения как последовательности строк.
Теперь перейдем с самому сглаживанию.
Тут все очевидно, единственное, что может быть не совсем очевидно для новичков в Fortran — это вложенность циклов, а именно — цикл по
В конце программы сохраним полученное сглаженное изображение и освободим память.
Процедура
Осталось определить функцию
→ Ссылка на полный код программы
Компилировал все через gfortran следующей командой (при условии, что все файлы лежат в одной директории):
Для начала сравним размытие фильтра Перона и Малика с гауссовым размытие при
одинаковых
Исходное изображение.

Сгладим это изображение фильтром Гаусса и фильтром анизотропной диффузии.

Рассмотрим еще одно изображение.

Сглаживание фильтром Гаусса (

Сглаживание фильтром Перона и Малика (

Отлично видно как гауссово размытие сильно смазывает границы областей, в то время как фильтр анизотропной диффузии в целом сохраняет их.
Поэкспериментируем теперь с параметрами. Будем варьировать

Заметим, что границы больших областей не смещаются при увеличении
Посмотрим как поведет себя алгоритм для разных шагов по времени (

Изображения получились практически идентичные. Теперь попробуем нарушить условие устойчивости.

Как мы видим, при небольших отклонениях некоторое размытие еще происходит, но начинают появляться артефакты. При
Была рассмотрена одна из возможных аппроксимаций фильтра анизотропной диффузии. В целом можно провести эксперименты с другими функциями , ввести функцию анализа зашумленности для автоматического подбора параметра
, ввести функцию анализа зашумленности для автоматического подбора параметра  .
.
В сравнении с гауссовым размытием видно, что фильтр действительно хорошо сохраняет границы областей. При этом алгоритм достаточно затратен для расчетов по сравнению с классическим фильтром Гаусса и не может быть также хорошо оптимизирован. Поэтому фильтр Перона и Малика в основном используется в задачах, где не требуется работа в реальном времени, а больше важна точность.
Повторно приведу ссылки на исходные коды: модуль для работы с PGM, реализация фильтра.
В статье я кратко рассмотрю зачем нужен этот фильтр, теорию по нему и как его реализовать алгоритмически, приведу код на языке Fortran и примеры сглаженных изображений.

Крайнее левое изображение — оригинальное, справа от оригинального — фильтрованные с различными параметрами.
Введение
В обработке изображений (особенно в машинном зрении) не редко встают задачи сегментации или выделения границ областей. Но если изображение получается как результат обработки информации с некоторого физического устройства как фотоаппарат, томограф и т.д., то оно обычно зашумлено, причем природа шумов на изображении может быть разная — как вызванная физическими явлениями, так и различными алгоритмическими и аппаратными особенностями.
Шумы сильно усложняют задачи сегментации и выделения границ, поэтому, обычно, такие изображение сперва пропускают через некоторые сглаживающие фильтры, которые помимо сглаживания шумов, сглаживают и все остальное, что хорошо для той же сегментации, ведь несущественных деталей становится меньше. Изображение, если рассматри��ать его как функцию двух переменных, становится более гладким, что существенно облегчает выделение областей на нем.
Тем не менее, при использовании таких фильтров мы еще и сглаживаем границы областей внутри изображения. То есть, чем сильнее сглаживание, тем больше мы отходим от изначальных границ. В некоторых задачах это может быть допустимо, но, например, в медицине, в автоматической сегментации снимков томографии различных частей человеческого тела, важно сохранить изначальные границы областей (здесь в роли областей выступают внутренние органы, их деформации, различные опухоли и т.д.).
Формального математически строго определения границы области для произвольного изображения не существует (это бы решило очень много проблем в теории обработки изображений).
Фильтр Перона и Малика
Впервые был описан в статье указанных математиков в 1990 году (ссылка на статью приведена в «источниках» в конце поста). Не будем вдаваться в глубокие теоретические детали, а хотя бы поверхностно рассмотрим как работает фильтр.
Здесь и далее рассматриваются изображения в градациях серого. Для цветных можно проводить сглаживания по каждому каналу независимо.
Теория
Итак, в фильтре анизотропной диффузии сглаженное изображение представляет собой некоторый член семейства изображений, полученных решением следующего уравнения математической физики:
C начальным условием:
Где:
С точки зрения теории, изображение — это некоторая непрерывная функция двух переменных, а сама картинка (матрица пикселей) — дискретизация этой функции. Причем 0 соответствует нулевой яркости точки изображения, то есть обозначает черный цвет.
По своей сути фильтр анизотропной диффузии является модификацией фильтра Гаусса.
Если подставить вместо, пока еще не рассмотренной, функции
Математики Коендеринк и Гумел показали, что такое семейство размытых изображений по параметру
Где:
Очевидно, функция
Исходя из уравнения фильтра (1), для сохранения изначального значения в точке изображения нужно, чтобы производная по времени равнялась нулю (то есть значение на любых слоях размытия было константой). Получаем следующие условия на функцию
Перона и Малик использовали градиент функции изображения
Где
Из-за нечеткого определения границ через норму градиента, требуют также, чтобы функция
Перона и Малик предложили два варианта функции
Где
Рассмотрим детальнее вторую функцию (формула 3). Для этого построим графики функции

Видно, что чем больше
Например, пусть в некоторой точке изображения, назовем ее
Таким образом,
Дискретизация
Для того чтобы перейти непосредственно к алгоритму фильтра, произведем дискретизацию уравнения. Достаточно простой с точки зрения математических выкладок и нетребовательной к вычислениям будет дискретизация уравнения методом конечных разностей. Для удобства перепишем основное уравнение:
Теперь запишем конечно-разностную явную схему:
Записать условие устойчивости для получившейся явной схемы — нетривиальная задача из-за нелинейности уравнения. Но Перона и Малик определили, что при
Где:
Для расчета коэффициентов
Хотя это достаточна грубая замена, аппроксимирующая несколько другое уравнение диффузии, она тем не менее также обеспечивает сохранение общей яркости изображения, а также дает практически идентичные результаты в сравнении с более точной аппроксимацией нормы градиента, выигрывая у последней в скорости вычислений.
Окончательно расчетная формула будет выглядеть так:
Где:
Схематично расчетную схему можно изобразить как на рисунке ниже.

То есть новое значение зависит от текущего значения и значений четырех соседей ячейки матрицы. Возникает вопрос — как пересчитывать граничные ячейки, ведь расчетная схема в таком случае будет выходить за пределы матрицы.

Чтобы фильтр менял значения яркости в ячейках в рамках максимума и минимума яркости исходного изображения, процесс, описанный основным уравнением, должен быть адиабатическим. Отсюда имеем граничное условие Дирихле вида:

Алгоритм и реализация на языке Fortran
Исходя из расчетной формулы в памяти всегда придется держать как минимум два двумерных массива, первый будет соответствовать оригинальному изображению, второй — размытому. Если провести аналогию с фильтром Гаусса, то для размытия изображения с радиусом
Последовательность действий будет примерно такая:
- Определяем ширину и высоту изображения (назовем w и h соответственно);
- Выделяем память под двумерный массив размерностью (w+2)*(h+2) (назовем I);
- Выделяем память под двумерный массив размерностью (w+2)*(h+2) (назовем BlurI);
- Заполняем массив нулями I=0;
- Считываем изображение и записываем данные пикселей в центр массива I (то есть оставляем слева, справа, сверху, снизу по одному нулевому столбцу или строке);
- Повторяем пока level<t (вначале level=0);
- Пересчитываем по формуле 4 все ячейки массива I, учитывая смещенную индексацию из-за нулевых полей. Считаем, что
— это BlurI, а
— I;
- Заменяем данные изображение в I на BlurI;
- Увеличиваем счетчик, level=level+deltaT, где deltaT — параметр, шаг по времени;
- Пересчитываем по формуле 4 все ячейки массива I, учитывая смещенную индексацию из-за нулевых полей. Считаем, что
- Создаем и сохраняем изображение из данных массива BlurI. Это наше размытое изображение;
- Освобождаем память, выходим из программы;
Для цветных изображений принцип действий сохраняется, но пересчет нужно выполнять для каждого канала отдельно.
Реализация на Fortran
На самом деле алгоритм достаточно тривиальный и легко может быть запрограммирован на многих популярных языках. Я в свое время столкнулся с трудностью реализации на фортране, так как долгое время не мог найти хорошего мануала или учебника по языку. Поэтому хочу привести реализацию именно на этом языке, в надежде, что кому-нибудь это пригодится.
Как ни странно, основная трудность при программировании заключалась в считывании картинки. В фортране отсутствуют встроенные процедуру (в языке их называют «сабрутинами») для манипуляций с изображениями, но есть все, что нужно для реализации своих процедур.
Самым простым форматом, который к тому же понимают и многие графические редакторы, мне показался PGM P5. Это открытый формат хранения растровых изображений типа bitmap без сжатия в оттенках серого. У него простой ASCII заголовок, а само изображение есть последовательность однобайтных (для оттенков серого от 0 до 255) целых чисел без знака. Подробнее о формате вы можете прочитать непосредственно в самом стандарте, ссылка приведена в разделе источников.
Я оформил процедуру для работы с PGM в виде модуля, подробно разбирать его не буду, так как это не относится к основной теме, приведу только ссылку на исходный код. Данный модуль работает только с изображениями с максимальным значением серого в 255.
Начнем программу с подключения модуля для работы с PGM и объявления всех необходимых переменных.
program blur
use pgmio
implicit none
double precision, parameter :: t=10.0d0, deltaT=0.2d0, k=10.0d0
character*(*), parameter :: input='dif_tomography.pgm', output='output.pgm'
double precision, allocatable :: u(:,:), nu(:,:)
double precision :: north, south, east, west, level
integer :: w, h, offset, n, i, j
end program blur
Параметр
t — это уровень размытия, на котором мы хотим прекратить работу алгоритма, deltaT — шаг по времени, k — параметр для пока еще не описанной функции g. Input и output — файл с исходным изображением и выходной файл соответственно.Теперь считаем размеры входного изображения в переменные
w и h.call pgmsize(input, w, h, offset)
Offset определяет количество байт, отведенных на заголовок изображения.Выделим память для массива изображения и массива сглаженного изображения и считаем в первый данные из файла
input.allocate(u(0:w+1,0:h+1))
u=0
allocate(nu(w,h))
call pgmread(input, offset, w, h, u, 0, 0)
Фортран позволяет программисту самому определ��ть индекс первого элемента в массиве, поэтому, учитывая, что вокруг изображения должны быть нули, заранее заполняем матрицу u нулями, задав ей размер от
0 до w+1 по первому измерения, и от 0 до h+1 по второму. Это позволит при дальнейшем пересчете использовать естественную индексацию без смещения.Процедура
pgmread считываем w*h байт, пропуская offset байт (занимаемых заголовком PGM) в массив u. Последние два параметра сообщают процедуре, что отсчет в матрице u начинается с нуля по каждому измерению. Хотя в данном случае это неважно, хочу отметить, что изображение будет считано в транспонированном виде, так как фортран хранит двумерные массивы как последовательности столбцов, а формат PGM хранит изображения как последовательности строк.
Теперь перейдем с самому сглаживанию.
level = 0 !счетчик уровня сглаживания
do while (level<t)
do j=1,h
do i=1,w
north = u(i-1,j)-u(i,j)
south = u(i+1,j)-u(i,j)
east = u(i,j+1)-u(i,j)
west = u(i,j-1)-u(i,j)
nu(i,j) = u(i,j) + deltaT*(g(north)*north+g(south)*south+g(east)*east+g(west)*west)
end do
end do
u(1:w,1:h) = nu(1:w,1:h) !заменяем оригинальное на размытое
level = level + deltaT
end do
Тут все очевидно, единственное, что может быть не совсем очевидно для новичков в Fortran — это вложенность циклов, а именно — цикл по
j идет раньше цикла по i. Все, опять же, из-за того, что фортран хранит двумерные массивы в памяти как последовательности столбцов. Если помять циклы местами, программа также будет работать, но значительно медленнее — программа будет обходить память не последовательно, �� перебегать из разных ячеек «туда-сюда».В конце программы сохраним полученное сглаженное изображение и освободим память.
deallocate(u)
call pgmwriteheader(output, w, h)
call pgmappendbytes(output, nu, 1, 1)
deallocate(nu)
Процедура
pgmwriteheader создает файл output и записывает в него заголовок PGM P5. Процедура pgmappendbytes записывает в конец файла output последовательность байт из nu, учитывая, что индексы nu начинаются с 1 по обоим измерениям. Замечу, что pgmappendbytes записывает байты из двумерного массива опять же в порядке столбцов, поэтому, хотя в памяти и находилось транспонированная версия изображения, при записи изображение транспонируется обратно.Осталось определить функцию
g. Например, реализуем функцию по формуле 3. contains
function g(x) result(v)
implicit none
double precision, intent(in) :: x
double precision :: v
v = 1/(1+(x/k)**2)
end function g
→ Ссылка на полный код программы
Компилировал все через gfortran следующей командой (при условии, что все файлы лежат в одной директории):
gfortran pgmio.f90 blur.f90
Примеры работы фильтра
Для начала сравним размытие фильтра Перона и Малика с гауссовым размытие при
одинаковых
t.Исходное изображение.

Сгладим это изображение фильтром Гаусса и фильтром анизотропной диффузии.

Рассмотрим еще одно изображение.

Сглаживание фильтром Гаусса (
t=10).
Сглаживание фильтром Перона и Малика (
t=10, k=8).
Отлично видно как гауссово размытие сильно смазывает границы областей, в то время как фильтр анизотропной диффузии в целом сохраняет их.
Поэкспериментируем теперь с параметрами. Будем варьировать
k при одинаковых t и deltaT (t=10, deltaT=0.2).
Заметим, что границы больших областей не смещаются при увеличении
k. Но более мелкие области постепенно начинают сливаться. При достаточно большом k фактически получим гауссово размытие, так как условие на границу не пройдет ни одна точка.Посмотрим как поведет себя алгоритм для разных шагов по времени (
t=10,k=5).
Изображения получились практически идентичные. Теперь попробуем нарушить условие устойчивости.

Как мы видим, при небольших отклонениях некоторое размытие еще происходит, но начинают появляться артефакты. При
deltaT=10 они уже заполняют все изображение.Заключение
Была рассмотрена одна из возможных аппроксимаций фильтра анизотропной диффузии. В целом можно провести эксперименты с другими функциями
В сравнении с гауссовым размытием видно, что фильтр действительно хорошо сохраняет границы областей. При этом алгоритм достаточно затратен для расчетов по сравнению с классическим фильтром Гаусса и не может быть также хорошо оптимизирован. Поэтому фильтр Перона и Малика в основном используется в задачах, где не требуется работа в реальном времени, а больше важна точность.
Повторно приведу ссылки на исходные коды: модуль для работы с PGM, реализация фильтра.
