
Комментарии 44
Я мало что понимаю в такой математике, но выглядит круто! Вот интересно, можно ли на основании всех этих закономерностей и корелляций вывести формулу рассчёта произвольного простого числа?
Очень интересно, на чем и как считал автор статьи. Когда речь заходит о 10 000 000 простых чисел 40 порядка, речь идет явно не о паре минут на домашнем процессоре)
Это не так сложно, если нужны именно числа после 40 порядка (речь же о двоичной системе?), То считаем простые числа решетом Эратосфена или Аткина до, примерно, 20+ порядка все простые числа, а затем ищем одним из этих же алгоритмов числа после 40 порядка, зная распределение простых чисел, можно предположить, что нам понадобится проверить не больше 10^9. Итого, алгоритм работает за O(2^k+n*k), где k=20, n = 10000000
Могу подробнее об этом статью написать, но идея в том, что на домашнем компьютере это считается пару секунд:)
Пару секунд на одном ядре уж точно не может считаться) про 8 ядер врать не буду, но полагаю, длительность все таки на порядок выше)
В общем, всё довольно просто. Если взять Скатерть Улама и сложить её вдоль горизонтальных или вертикальных магистралей, как лист бумаги, то можно заметить, что простые числа не накладываются друг на друга (за исключением чисел 2 и 19, если складывать по вертикальной магистрали).
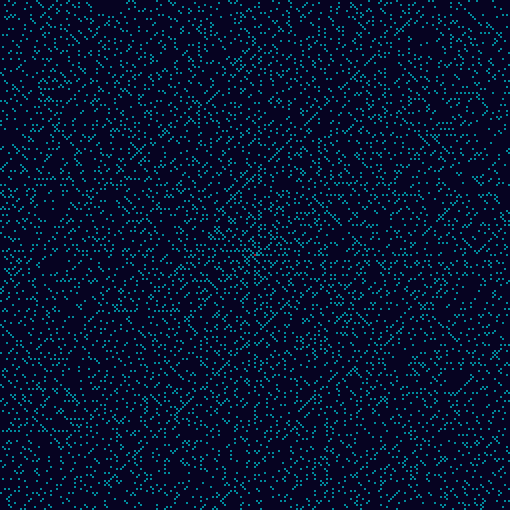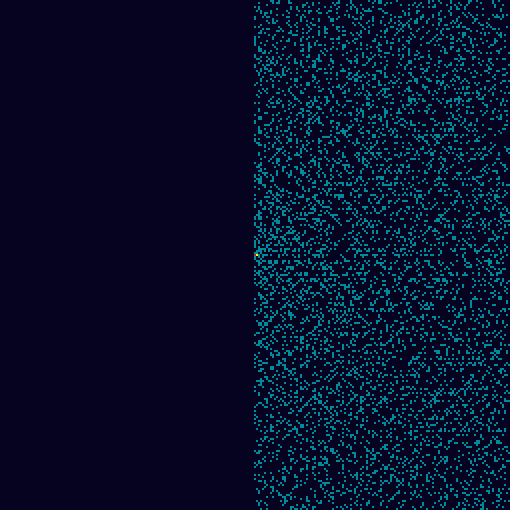

На больших по размеру скатертях не проверял, но было бы интересно. Эх, вот бы найти способ сложения Скатерти Улама таким образом, чтобы пустот между простыми числами не было вообще. Гранд-мастера оригами, ау! :D

возможно там что то типа Пуасона с математическим ожиданием n/ln(n)
познавательно, спасибо автору.
Есть ли название для такого преобразования? Я просто буду называть его «изгиб».
Чем-то напоминает преобразование Барроу-Уиллера (BWT)
А чаще всего она 2 :)


(В подписях снизу указана половина каждого числа, т.е. там где 105 — это на самом деле 210 и т. д.).
для праймориала он равен радикалу.
При любом основании >= 2 будет не более одного простого числа, запись которого заканчивается на 0. Этот факт не дает почти ничего.
Можно посмотреть как простые числа записываются в Фиббоначиевой СС.
Более того, N+-1/2(4,6) что как раз и приводит к модулярной арифметике. Классика колеса простых вроде 2n+1, 4n+-1, 6n+-1, далее по праймориальному и праймориально-факториальному ядрам и ядрам содержащим квадратичный факториал как сжимающую добавку. Если говорить об очень больших простых и полупростых числах, то схема с праймориальным разложением очень интересна для компрессии представлений. Любое число представляется как k*prime(i)#+resedue, где k от 1 до prime(i+1)-1. Далее resedue раскладывается по праймориалам предыдущих простых. В отличие от обычных позиционных систем эта растет очень быстро, и что характерно, k можно раскладывать по вторичному праймориалу. Арифметика сложения и умножения не очевидна, зато симметрична по единственности разложения и не возникает ситуации с отсутствием факторизации по умножению и задаче кассира по сложению. При этом праймориальная форма представления чисел не менее экономична, чем логарифмическая, но гораздо более проста при сложении, логарифм суммы - очень неочевидная вещь, а праймориал суммы, как и сумма праймориалов поддается довольно простым преобразованиям. Кстати праймориальные корни тоже хорошо выражаются аналитически, в отличие от дискретных логарифмов. Но я только в самом начале исследования, так что пока это больше интуитивные идеи и наблюдения
Кстати есть классная программа https://github.com/kimwalisch/primesieve
Если вам нужно сгенерировать простые числа.
Я как-то решил написать программу на 10^9 строк кода генерирующую число pi использующую последовательность простых чисел. Программу написал на C она занимала несколько гигабайт и gcc отказывался её компилировать)
А вот мой генератор простых числел на C.
Очень рекомендую посмотреть на картину с учетом полуцелых чисел. То есть рассматривать делимость с учетом полуцелых чисел. Вроде бы кажется тривиальным, что там может появиться от общего умножения на 2, но это совершенно другие закономерности


Из моих исследований полупростых чисел :)
Структура и случайность простых чисел