The_Freeman 25 дек 2018 в 16:08

О фракталах, мартингалах и случайных интегралах. Часть первая

12 мин

26K

Туториал

На мой взгляд, стохастические исчисления — это один из тех великолепных разделов высшей математики (наряду с топологией и комплексным анализом), где формулы встречаются с поэзией; это место, где они обретают красоту, место где начинается простор для художественного творчества. Многие из тех, что прочли статью Винеровский хаос или Еще один способ подбросить монетку, даже если и мало, что поняли, всё же смогли оценить великолепие этой теории. Сегодня мы с вами продолжим наше математическое путешествие, мы погрузимся в мир случайных процессов, нетривиального интегрирования, финансовой математики и даже немного коснемся функционального программирования. Предупреждаю, держите наготове свои извилины, так как разговор у нас предстоит серьезный.

Кстати, если вам интересно прочитать в отдельной статье, как вдруг оказалось, что

$dX^2 \neq 2X\cdot dX,$

я добавил внизу опрос, где вы можете оставить свой голос.

Скрытая угроза фракталов

Представьте себе какую-нибудь простую функцию $inline$ на некотором интервале $[t, t+\Delta t]$ . Представили? В стандартном математическом анализе мы привыкли к тому, что если размеры этого интервала достаточно долго уменьшать, то данная нам функция начинает вести себя довольно гладко, и мы можем приблизить её прямой, в крайнем случае, параболой. Все благодаря теореме о разложении функции, сформулированной английский ученым Бруком Тэйлором в 1715-м году:

$f(t+\Delta t) = f(t) + f'(t)\cdot \Delta t+\frac{1}{2}f''(t)\cdot (\Delta t)^2+\cdots$

Этой теоремой искусно орудуют современные математики-инженеры, аппроксимируя всё подряд для своих численных вычислений. Но на фракталах такая схема даёт сбой.

К тому моменту как Бенуа Мандельброт придумал само понятие «фракталов», они уже сотню лет не давали спать многим мировым ученым. Одним из первых, кому фракталы подмочили репутацию, стал Андре-Мари Ампер. В 1806 году ученый выдвинул довольно убедительное «доказательство» того, что любую функцию можно разбить на интервалы из непрерывных функций, а те в свою очередь, благодаря непрерывности, должны иметь производную. И многие его современники-математики с ним согласились. Вообще, Ампера нельзя винить в этой, с виду довольно грубой, ошибке. Математики начала XIX века имели довольно расплывчатое определение таких ныне столь базовых концепций мат.анализа как непрерывность и дифференцируемость, и, как следствие, могли сильно ошибаться в своих доказательствах. Не исключением были даже такие именитые ученые как Гаусс, Фурье, Коши, Лежандр, Галуа, не говоря уже о куда менее известных математиках тех времен.

Тем не менее, в 1872 году гипотезу о существовании производных у непрерывных функций опроверг Карл Вейерштрасс, представив на обозрение первого в мире фрактального монстра, всюду непрерывного и нигде не дифференцируемого.

Вот, к примеру, как задается подобная функция:

$f(t)=\sum_{n=0}^\infty \frac{\sin(2^n t)}{2^n}$

Таким же свойством обладает и Броуновское движение (кстати, почему-то не Брауновское, фамилия-то британская, всё же). Броуновское движение — это непрерывный случайный процесс $inline$ , такой что все его приращения независимы и имеют нормальное распределение:

$B(T)-B(t) \sim \mathcal{N}(0, T- t), \quad t < T.$

Траектории Броуновского движения являются фрактальными функциями, они непрерывны всюду и всюду негладки. Но если функция Вейерштрасса являлась лишь контрпримером, пускай и одним из ярчайших за всю историю математического анализа, то Броуновское движение обещало стать фундаментом стохастической теории, и с ним надо было как-то научиться работать.

Бесконечная вариация Броуновского движения

Давайте снова представим себе функцию $inline$ на интервале $t \in [0, T]$ и разобьем этот интервал на множество из $inline$ непересекающихся подынтервалов:

$\Pi = \{ 0 = t_0 < t_1 < \dots < t_n=T\}.$

Нам неважно как распределены точки $t_0, \dots, t_n$ , разбивающие этот интервал, куда более интересен размер максимального шага: $\| \Pi \| = \max_{i=1,\dots, n}(t_{i}-t_{i-1}).$ Мы назовем величину

$V_{[0,T]}^f=\lim_{\|\Pi \| \rightarrow 0} \sum_{i=1}^n |f(t_{i}) - f(t_{i-1})|$

вариацией (первого рода) функции $inline$ (также именуемой общей вариацией). Если $V_{[0,T]}^f < \infty$ , то мы скажем, что $inline$ обладает конечной вариацией. Например, вариация достаточно «гладкой» функции

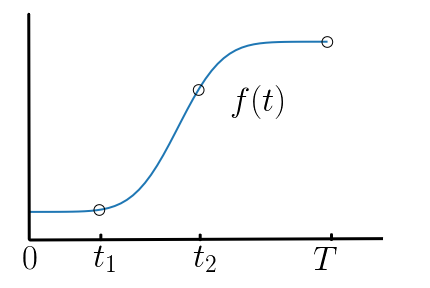
будет конечной. В каком случае мы не столь уверены? Ну, например, конечной вариации не будет у функции

$f(t)=1_\mathbb{Q}(t),$

возвращающей $inline$ для всех рациональных $inline$ и $inline$ для всех иррациональных. Подобную логику можно расширить и на случайные функции. Пускай $inline$ — это случайный процесс. Вариация для него задаётся аналогичным образом:

$V_{[0,T]}^X(\omega)=\lim_{\|\Pi \| \rightarrow 0} \sum_{i=1}^n|X(t_{i})-X(t_{i-1})|(\omega).$

Единственная разница — вариация тоже станет случайной (параметр $\omega$ можно для удобства опустить, но он здесь как бы намекает, что вариация от случайного процесса — это отображение из пространства случайных событий $\Omega$ в $\mathbb{R}$ ).

Вот, как будет выглядеть довольно простая реализация вариации на Хаскеле:

-- | 'totalVariation' calculates total variation of the sample process X(t)
totalVariation :: [Double] -- process trajectory X(t)
               -> Double   -- V(X(t))
totalVariation x@(_:tx) = sum $ zipWith (\x xm1 -> abs $ x - xm1) tx x

Где в реальном мире встречаются случайные процессы? Один из известнейших примеров сегодня — финансовые рынки, а именно движение цен на валюту, акции, опционы и различные ценные бумаги. Пускай $inline$ — это стоимость акции Apple. В какой-то момент времени вы решили купить $inline$ акций по цене $inline$ , а через некоторый промежуток времени цена изменилась и стала равна $inline$ . В результате у вас $f(t_0) \cdot \Delta X(t_1)$ чистой прибыли/убытка, где $\Delta X(t_i) = X(t_i)-X(t_{i-1})$ . Вы решили докупить/продать часть акций и теперь вы держите на руках $inline$ ценных бумаг. Через некоторое время ваш доход/потери составят $f(t_0) \cdot \Delta X(t_1) + f(t_1) \cdot \Delta X(t_2)$ , и т.д. В конце концов, вы заработаете/потеряете

$I(T) = \sum_{i=1}^n f(t_{i-1}) \cdot \Delta X(t_i) .$

Все довольно просто, но вот загвоздка: процесс изменения цены на акцию может двигаться очень быстро, как и наш процесс её покупки/продажи (так называемый High Frequency Trading). Хотелось бы расширить эти вычисления на непрерывные процессы и представить наши доходы в виде интеграла наподобие $I(T) = \int_0^T f(t)dX(t).$ Проблема в том, что мы пока не знаем каким образом брать интегралы по случайным процессам и их траекториям. Но мы помним по какому принципу определяется стандартный интеграл Лебега(-Стилтьеса). Обычно сначала нужно задать соответствующую меру. Возьмем неубывающий процесс $inline$ , для простоты начинающийся с нуля: $inline$ , и неотрицательную меру, соответствующую его приращениям

$\mu_X(a,b]:=X(b)-X(a).$

Если функция $inline$ ограниченная и измеримая (вспоминаем функциональный анализ) мы можем определить для неё интеграл на интервале $inline$ в виде

$\int_0^T f(t)dX(t) = \int_{[0, T]} f(t)\mu_X(dt).$

Для общего случая, если траектории случайного процесса не обладают монотонностью, мы можем разделить его на два неубывающих процесса: $inline$ и тогда мы определим интеграл Лебега как

$\int_0^T f(t)dX(t) = \int_{[0,T]} f(t) \mu_{X^+}(dt) - \int_{[0,T]} f(t) \mu_{X^-}(dt).$

Необходимое условие для существования такого интеграла — это существование $V_{[0,T]}^X$ . Действительно, если наш процесс состоит из разницы двух неубывающих процессов, то у него существует конечная вариация (во второй строке мы воспользовались неравенством треугольника):

$\begin{aligned} V_{[0,T]}^X &= \lim_{\|\Pi \| \rightarrow 0} \sum_{i=1}^n |X(t_{i})-X(t_{i-1})| \\ & \leq \lim_{\|\Pi \| \rightarrow 0} \Big( \sum_{i=1}^n |X^+(t_{i})-X^+(t_{i-1})| + \sum_{i=1}^n |X^-(t_{i})-X^-(t_{i-1})| \Big) \\ & = X^+(T)+ X^-(T) < \infty. \end{aligned}$

Кстати, это условие работает и в обратном направлении: если у нас есть процесс $inline$ с конечной вариацией, то мы можем определить $X^+(t)=\frac{1}{2}(|X(t)| + X(t))$ и $X^-(t)=\frac{1}{2}(|X(t)|-X(t))$ . Монотонность и равенство $inline$ легко доказываются.

Теперь мы с легкостью можем что-нибудь проинтегрировать. Возьмем траекторию какого-нибудь непрерывного случайного процесса и обзовём её $inline$ . С помощью теоремы Лагранжа о среднем можно показать, что для непрерывной функции $inline$ вариация будет равна $V_{[0,T]}^g = \int_0^T |g'(t)|dt$ . Если этот интеграл существует, то при упомянутых выше условиях ограниченности и измеримости $inline$ мы сможем посчитать

$\int_0^Tf(t)dg(t) = \int_0^Tf(t)g'(t)dt.$

Это действительно несложно. А как насчет фракталов, траекторий типа монстра Вейерштрасса? Ведь для них не существует $inline$ .

Итак вопрос: можно ли взять интеграл в смысле Лебега от Броуновского движения? Посчитаем вариацию, и если она будет конечной, то у нас не должно быть никаких проблем. Давайте зайдем со стороны так называемой квадратичной вариации:

$[B](T)= \lim_{\|\Pi\| \rightarrow 0} \sum_{i=1}^n \big(B(t_{i+1})-B(t_i)\big)^2$

Чему, по-вашему, равен этот предел? Мы рассмотрим случайную величину $inline$ и покажем, что её дисперсия равняется нулю:

$\begin{aligned}\sum_{i=1}^n \big(B(t_{i+1})-B(t_i)\big)^2-T&=\sum_{i=1}^n \Big( \big( B(t_{i+1}) - B(t_i) \big)^2-(t_{i+1}-t_i)\Big)\\ &= \sum_{i=1}^n (Z_i^2-1)(t_{i+1}-t_i),\end{aligned}$

где

$Z_i = \frac{B(t_{i+1}) - B(t_i)}{\sqrt{t_{i+1} - t_i}} \sim \mathcal{N}(0,1)$

стандартная нормально распределенная величина. В частности, так как все $inline$ независимы и имеют распределение хи-квадрат со степенью 1, несложно подсчитать, что

$\mathbb{E}[(Z_i^2-1)^2]=\operatorname{Var}(Z_i^2)=2.$

Следовательно,

$\begin{aligned} \mathbb{E}\bigg[\Big( \sum_{i=1}^n \big(B(t_{i+1})-B(t_i)\big)^2 -T\Big)^2\bigg]&=\sum_{i=1}^n \mathbb{E}[(Z_i^2-1)^2(t_{i+1}-t_i)^2]\\ &=2\sum_{i=1}^n (t_{i+1}-t_i)^2 \\ & \leq \| \Pi \| \cdot 2\sum_{i=1}^n (t_{i+1}-t_i) \rightarrow 0. \end{aligned}$

Иначе говоря,

$display$

Запомните эту формулу! Она является фундаментом стохастического анализа, своеобразным местным аналогом центральной предельной теоремы, и все остальные теоремы явно и неявно крутятся вокруг неё.

Заметьте, что $[B](T) = \operatorname{Var}(B(T))$ , однако методы подсчёта этих двух величин совсем разные. Дисперсия Броуновского движения считается усреднением всех его траекторий, учитывая их вероятности. Квадратичная вариация же берется из одной единственной случайной траектории, по которой произошло движение, и вероятности здесь роли не играют. В то время как дисперсия может быть посчитана только теоретически, так как требует усреднения всех реализаций, квадратичная реализация может быть посчитана явно (с достаточным значением дискретизации данных). Указанная выше формула интересна в частности тем, что по определению квадратичная вариация, как и вариация первого рода $V_{[0,T]}^X$ является случайной величиной. Однако, фича Броуновского движения в том, что его квадратичная вариация вырождается и принимает лишь одно единственное значение, соответствующее длине интервала, независимо от того, по какой траектории происходило движение.

Напишем код, считающий квадратичную вариацию реализации случайного процесса $inline$ :

-- | 'quadraticVariation' calculates quadratic variation of the sample process X(t)
quadraticVariation :: [Double] -- process trajectory X(t)
                   -> Double   -- [X(t)]
quadraticVariation x@(_:tx) = sum $ zipWith (\x xm1 -> (x - xm1) ^ 2) tx x

Итак, теперь мы готовы вернуться к подсчету интересующей нас вариации $V_{[0,T]}^B$ . Мы выяснили, что

$\lim_{\| \Pi \|\rightarrow 0} \sum_{i=1}^n ( B(t_{i+1}) - B(t_i) )^2=T.$

То есть, это ненулевая, но и не бесконечная величина. С другой стороны, она ограничена сверху максимальным шагом разбитого $inline$ :

$\begin{aligned} \sum_{i=1}^n ( B(t_{i+1}) - B(t_i) )^2 \leq \max\big \{ |B(t_{i+1}) - B(t_i)| \big| (t_{i}, t_{i+1})\subset \Pi \big\} \cdot \sum_{i=1}^n |B(t_{i+1})-B(t_i)| . \end{aligned}$

Мы знаем, что Броуновское движение — процесс непрерывный, а значит

$\max\big \{ |B(t_{i+1}) - B(t_i)| \big| (t_{i}, t_{i+1})\subset \Pi \big\} \rightarrow 0.$

Однако, $\sum_{i=1}^n | B(t_{i+1}) - B(t_i) | \rightarrow V_{[0,T]}^B.$ И, как следствие,

$V_{[0,T]}^B = \infty.$

Н-да…

Интеграл Ито или Новая надежда

В 1827 году английский ботаник Роберт Браун, наблюдая пыльцевые зерна в воде через микроскоп, заметил, что частицы внутри их полости двигаются определенным образом; однако он тогда не смог определить механизмы, вызывавшие это движение. В 1905 году Альберт Эйнштейн опубликовал статью, в которой подробно объясняется, как движение, наблюдаемое Брауном, было результатом того, что пыльца перемещается отдельными молекулами воды. В 1923 году вундеркинд и «отец кибернетики» Норберт Винер написал статью о дифференцируемых пространствах, где подошел к этому движению со стороны математики, определил вероятностные меры в пространстве траекторий и, используя концепцию интегралов Лебега, заложил фундамент стохастического анализа. С тех пор в математическом сообществе Броуновское движение также именуется Винеровским процессом.

В 1938 году выпускник Токийского университета Киёси Ито начинает работать в Бюро по статистике, где в свободное время знакомится с работами основателя современной теории вероятности Андрея Колмогорова и французского ученого Поля Леви, изучающего на тот момент различные свойства Броуновского движения. Он пытается соединить воедино интуитивные видения Леви с точной логикой Колмогорова, и в 1942 году пишет работу «О стохастических процессах и бесконечно делимых законах распределения», в которой реконструирует с нуля концепцию стохастических интегралов и связанную с ней теорию стохастических дифференциальных уравнений, описывающих движения, вызванные случайными событиями.

Интеграл Ито для простых процессов

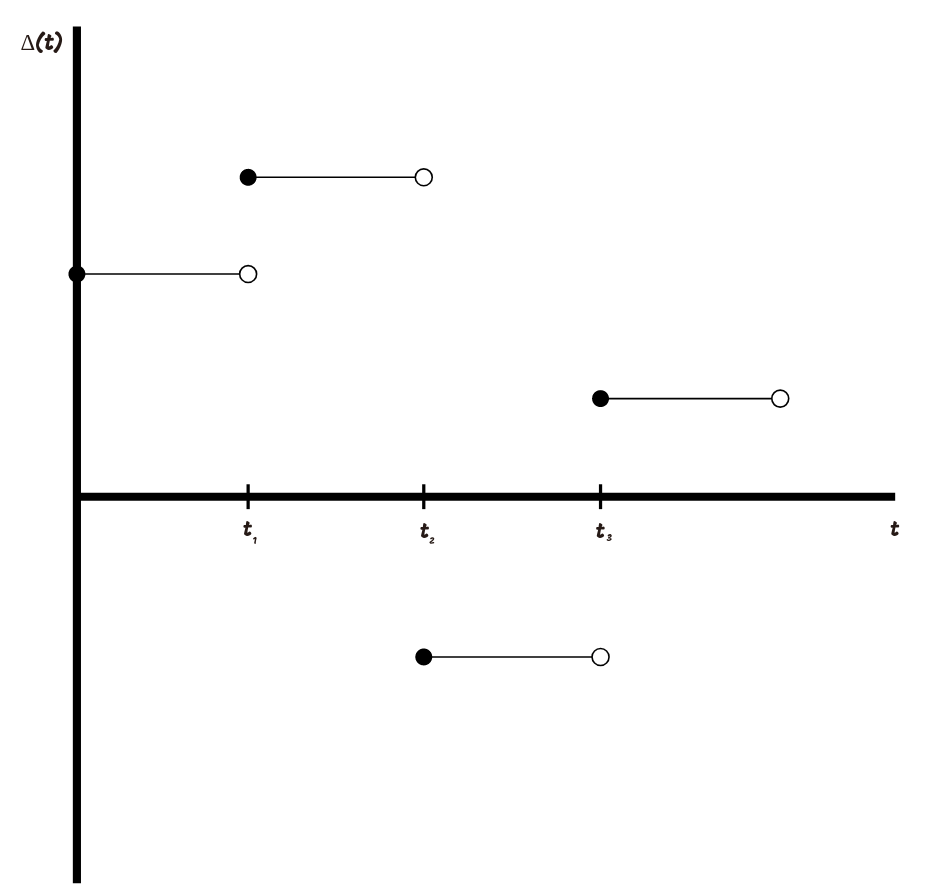
Ито разработал довольно простой способ построения интеграла. Для начала мы определим интеграл Ито для простого кусочно-постоянного процесса $\Delta(t)$ , а затем расширим это понятие на более сложные интегранды. Итак, пускай у нас снова есть разбиение $\Pi = \{ 0 = t_0 < t_1 < \dots < t_n=T\}$ . Мы считаем, что значения $\Delta(t)$ постоянны на каждом интервале $[t_j, t_{j+1})$

Представим, что $inline$ — это стоимость какого-либо финансового инструмента в момент $inline$ (Броуновское движение может принимать отрицательные значения, поэтому это не очень хорошая модель для движения цены, но сейчас мы это проигнорируем). Пускай также $t_0, t_1, \dots, t_{n-1}$ — это торговые дни (часы/секунды, не важно), а $\Delta(t_0), \Delta(t_1,), \dots, \Delta(t_{n-1})$ — это наши позиции (количество финансовых инструментов на руках). Мы считаем, что $\Delta(t)$ зависит только от информации, известной в момент $inline$ . Под информацией я имею ввиду траекторию Броуновского движения до этого момента времени. Тогда наш доход будет составлять:

$I(t) = \sum_{j=0}^k \Delta(t_j) [B(t_{j+1}-B(t_j)] + \Delta(t_k)[B(t)-B(t_k)].$

Процесс $inline$ называется интегралом Ито для простого процесса $\Delta(t)$ и мы будем его записывать в виде

$I(t)=\int_0^t \Delta(s)dB(s).$

У этого интеграла есть несколько интересных свойств. Первое и довольно очевидное: в начальный момент его математическое ожидание в любой точке равно нулю:

$\mathbb{E}[I(t)] = 0.$

Более того, интеграл Ито является мартингалом, но об этом позже.

Расчет второго момента/дисперсии уже требует дополнительных расчётов. Пускай $D_j=B(t_{j+1})-B(t_j)$ для $j=1, \dots, k-1$ и $inline$ . Тогда мы можем переписать интеграл Ито в виде

$I(t) = \sum_{j=0}^k \Delta(t_j)D_j.$

Воспользовавшись тем, что $\mathbb{E}[D_j]=0$ и тем, что $inline$ и $inline$ независимы для $i \neq j$ мы можем рассчитать

$\begin{aligned} \mathbb{E}[I^2(t)] &=\mathbb{E}\Big[ \sum_{j=0}^k \Delta^2(t_j)D_j^2 + 2\sum_{0 \leq i < j \leq k}\Delta(t_i)\Delta(t_j) D_iD_j\Big] \\ &= \sum_{j=0}^k \mathbb{E}\Big[ \Delta^2(t_j) D_j^2 \Big] + 2 \sum_{0 \leq i < j \leq k} \mathbb{E}[\Delta(t_i)\Delta(t_j) D_iD_j] \\ &= \sum_{j=0}^k \mathbb{E}\Big[ \Delta^2(t_j) \Big] \cdot \mathbb{E}[D_j^2] + 2 \sum_{0 \leq i < j \leq k} \mathbb{E}[\Delta(t_i)\Delta(t_j) D_i] \cdot \mathbb{E}[D_j] \\ &= \sum_{j=0}^{k-1} \mathbb{E}\Big[ \Delta^2(t_j) \Big] (t_{j+1}-t_j) + \mathbb{E}[\Delta^2(t_k)](t-t_k) \\ &= \sum_{j=0}^k \mathbb{E} \Big[\int_{t_j}^{t_{j+1}} \Delta^2(s) ds\Big] + \mathbb{E} \Big[ \int_{t_k}^t \Delta^2(s)ds \Big] \\ &=\mathbb{E} \Big[ \int_{0}^t \Delta^2(s)ds \Big]. \end{aligned}$

Равенство

$\mathbb{E}[I^2(t)] = \mathbb{E}\Big[\int_0^t \Delta^2(s)ds \Big]$

называется изометрией Ито.

И, наконец, квадратичная вариация. Давайте сначала посчитаем вариацию на каждом интервале $[t_j, t_{j+1}]$ , где значения $\Delta(t)$ постоянны, а потом сложим их все вместе. Возьмем разбиение интервала $t_j = s_0 < s_1 < \cdots < s_m = t_{j+1}$ и рассмотрим

$\begin{aligned} \sum_{i=0}^{m-1} [I(s_{i+1}) - I(s_i)]^2 &= \sum_{i=0}^{m-1}[\Delta(t_j)(B(s_{i+1})-B(s_i))^2 \\ &=\Delta^2(t_j) \sum_{t=0}^{m-1} (B(s_{i+1})-B(s_i))^2 \\ &\xrightarrow[m \rightarrow \infty]{} \Delta^2(t_j)(t_{j+1}-t_j) \\ &=\int_{t_j}^{t_{j+1}}\Delta^2(s)ds. \end{aligned}$

Аналогично считается квадратичная вариация для интервала $inline$ . Суммируя все эти кусочки, мы получаем

$[I(t)]=\int_0^t \Delta^2(s)ds.$

Теперь мы можем ясно видеть разницу между дисперсией и вариацией. Если процесс $\Delta(t)$ является детерминированным, то они совпадают. Но если мы решим менять нашу стратегию в зависимости от траектории, по которой прошло Броуновское движение, то и вариация начнет меняться, в то время как дисперсия всегда равна определенному значению.

Интеграл Ито для сложных процессов

Теперь мы готовы расширить понятие интеграла Ито на более сложные процессы. Пускай у нас есть функция $inline$ , которая может непрерывно измениться во времени и даже иметь разрывы. Единственные предположения, которые мы хотим сохранить — это квадратичная интегрируемость процесса:

$\mathbb{E}\Big[ \int_0^T h^2(t)dt \Big] < \infty$

и адаптируемость, т.е. на момент $inline$ , когда мы знаем значение $inline$ , мы уже должны знать также значение $inline$ . В реальном мире мы не можем сначала узнать стоимость акций на завтра, а затем в них вложиться.

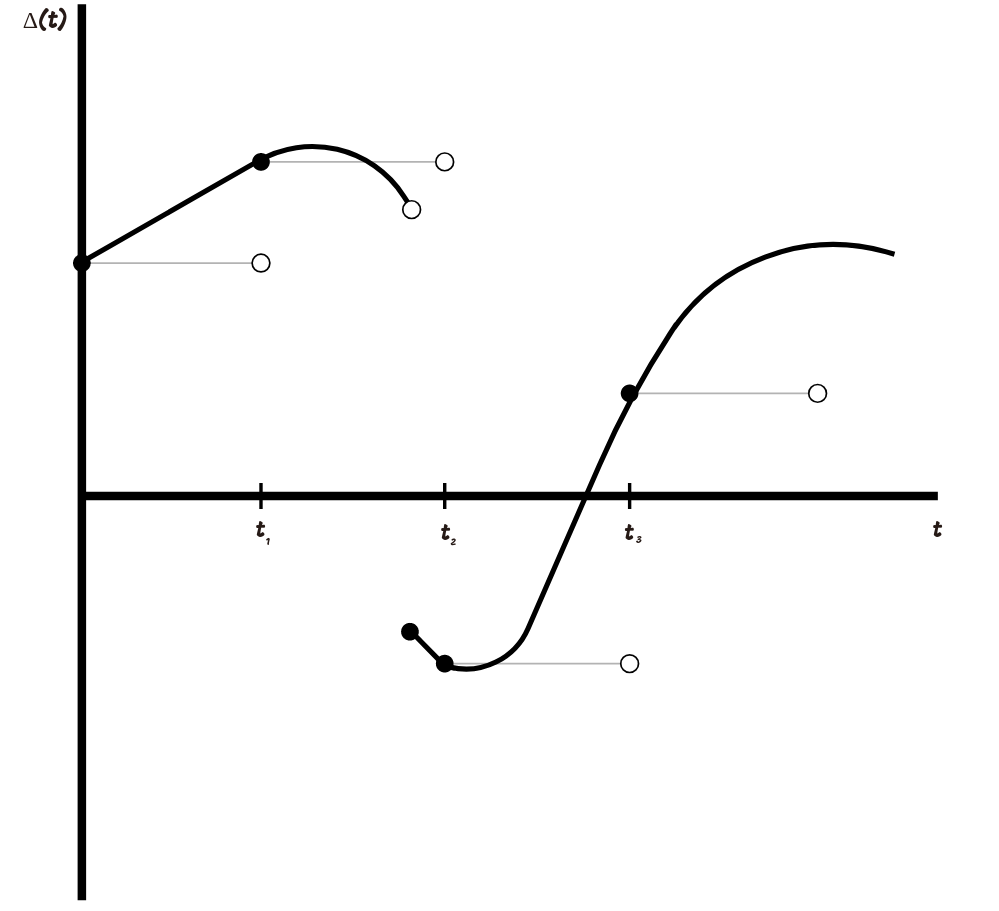
Для того, чтобы определить $\int_0^T h(t)dB(t)$ мы аппроксимируем $inline$ простыми процессами. На графике ниже показано, как это можно сделать.

Аппроксимация происходит следующим образом: мы выбираем разбиение $inline$ , затем создаем простой процесс, чьи значения равны $inline$ для каждого $inline$ и не изменяются на отрезке $[t_j, t_{j+1})$ . Чем меньше становится максимальный шаг нашего разбиения, тем ближе становится аппроксимирующий простой процесс к нашему интегранду.

В общем случае, возможно выбрать последовательность простых процессов $inline$ , такую что она будет сходиться к $inline$ . Под сходимостью мы имеем ввиду

$\lim_{n \rightarrow \infty} \mathbb{E}\Big[ \int_0^T |h_n(t)-h(t)|^2 dt \Big] = 0.$

Для каждого процесса $inline$ интеграл Ито уже определен и мы определяем интеграл Ито для непрерывно изменяющегося процесса как предел:

$\int_0^t h(s)dB(s) = \lim_{n \rightarrow \infty} \int_0^th_n(s)dB(s), \quad 0 \leq t \leq T.$

Интеграл Ито в общем случае обладает следующими свойствами:

Его траектории непрерывны
Он адаптирован. Логично, ведь в каждый момент времени мы должны знать наше значение дохода.
Он линеен: $\int_0^t h(s)dB(s) + \int_0^t f(s)dB(s) = \int_0^t(h(s)+f(s))dB(s).$
Он мартингал, но об этом ближе к концу статьи.
Сохраняется изометрия Ито: $\mathbb{E}[I^2(t)] = \mathbb{E}\Big[\int_0^t h^2(s)ds \Big]$ .
Его квадратичная вариация: $[I(t)]=\int_0^th^2(s)ds.$

Небольшая ремарка: для тех, кто хочет более подробно изучить конструирование интеграла Ито или вообще увлекается финансовой математикой, очень советую книгу Steven Shreve «Stochastic Calculus for Finance. Volume II».

Покодим?

Для последующих рассуждений мы будем обозначать интеграл Ито в несколько ином виде:

$I(h)=\int_{0}^T h(s)dB(s),$

для некоторого $inline$ . Таким образом, мы подготавливаем себя к мысли о том, что интеграл Ито — это отображение, действующее из пространства квадратично интегрируемых функций $inline$ в вероятностное пространство случайных процессов. Так например, можно перейти от старой нотации к новой:

$I(t) = \int_0^T h(s) \cdot 1_{[0,t]}(s)ds = I(h \cdot 1_{[0,t]}).$

В предыдущей статье мы реализовали Гауссовский процесс: $W: H \rightarrow L^2(\Omega, \mathcal{F}, \mathbb{P})$ . Мы знаем, что Гауссовский процесс — это отображение из гильбертова пространства в вероятностное, что по сути является обобщенным случаем интеграла Ито, отображения из пространства функций в пространство случайных процессов. Действительно,

data L2Map = L2Map {norm_l2 :: Double -> Double}

type ItoIntegral = Seed         -- ω, random state
                -> Int          -- n, sample size
                -> Double       -- T, end of the time interval
                -> L2Map        -- h, L2-function
                -> [Double]     -- list of values sampled from Ito integral

-- | 'itoIntegral'' trajectory of Ito integral on the time interval [0, T]
itoIntegral' :: ItoIntegral
itoIntegral' seed n endT h = 0 : (toList $ gp !! 0)
  where gp = gaussianProcess seed 1 (n-1) (\(i, j) -> norm_l2 h $ fromIntegral (min i j + 1) * t)
        t = endT / fromIntegral n

Функция itoIntegral' принимает на вход seed — параметр для генератора случайных величин, n — размерность выходного вектора, endT — параметр $inline$ и функцию h из класса L2Map, для которой определена функция norm_l2, возвращающая норму интегранда: $t \mapsto \int_0^t h^2(s) ds$ . На выходе itoIntegral выдает реализацию интеграла Ито на интервале $inline$ с частотой дискретизации, соответствующей параметру n. Естественно, подобный способ реализации интеграла Ито — это в некотором смысле overkill, но он позволяет настроиться на функциональное мышление, столь необходимое для дальнейших рассуждений. Мы запишем более быструю реализацию, не требующую работы с гигантскими матрицами.

-- | 'mapOverInterval' map function f over the interval [0, T]
mapOverInterval :: (Fractional a) => Int      -- n, size of the output list
                                  -> a        -- T, end of the time interval
                                  -> (a -> b) -- f, function that maps from fractional numbers to some abstract space
                                  -> [b]      -- list of values f(t), t \in [0, T]
mapOverInterval n endT fn = [fn $ (endT * fromIntegral i) / fromIntegral (n - 1) | i <- [0..(n-1)]]

-- | 'itoIntegral' faster implementation of itoIntegral' function
itoIntegral :: ItoIntegral
itoIntegral seed 0 _    _ = []
itoIntegral seed n endT h = scanl (+) 0 increments
  where increments = toList $ (sigmas hnorms) * gaussianVector
        gaussianVector = flatten $ gaussianSample seed (n-1) (vector [0]) (H.sym $ matrix 1 [1])
        sigmas s@(_:ts) = fromList $ zipWith (\x y -> sqrt(x-y)) ts s
        hnorms = mapOverInterval n endT $ norm_l2 h

Теперь с помощью этой функции, мы можем реализовать, например, обыкновенное Броуновское движение: $B(t) = \int_0^t dB(s)$ . Функция h будет функцией, у которой норма norm_l2 будет $t \mapsto \int_0^t ds = t$ , тождественной функцией.

l2_1 = L2Map {norm_l2 = id}

-- | 'brownianMotion' trajectory of Brownian motion a.k.a. Wiener process on the time interval [0, T]
brownianMotion :: Seed     -- ω, random state
               -> Int      -- n, sample size
               -> Double   -- T, end of the time interval
               -> [Double] -- list of values sampled from Brownian motion
brownianMotion seed n endT = itoIntegral seed n endT l2_1

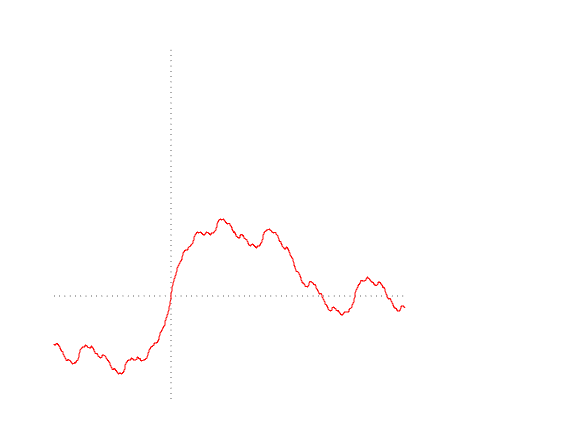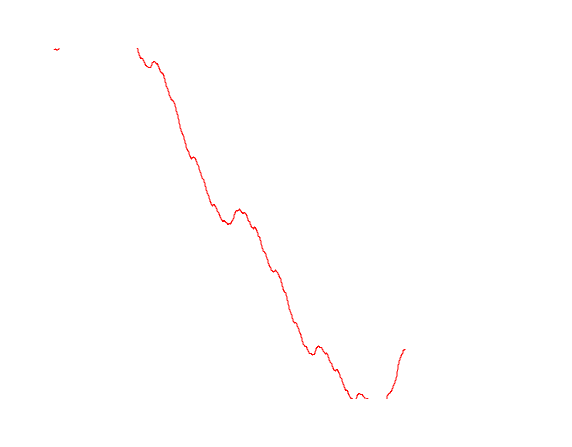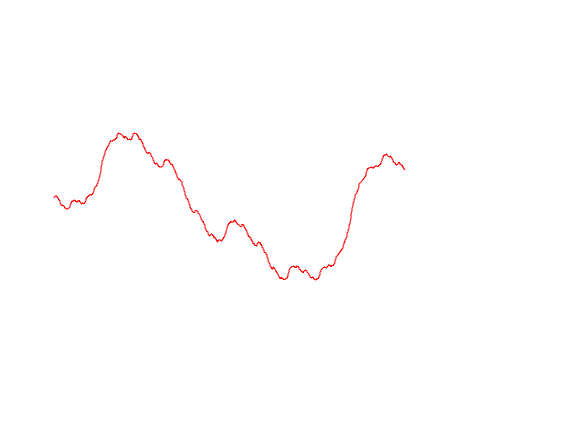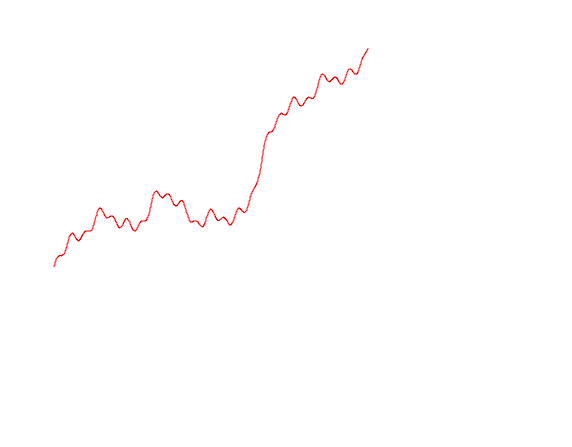
Попробуем нарисовать различные варианты траекторий Броуновского движения

import Graphics.Plot

let endT = 1
let n = 500
let b1 = brownianMotion 1 n endT
let b2 = brownianMotion 2 n endT
let b3 = brownianMotion 3 n endT
mplot [linspace n (0, lastT), b1, b2, b3]

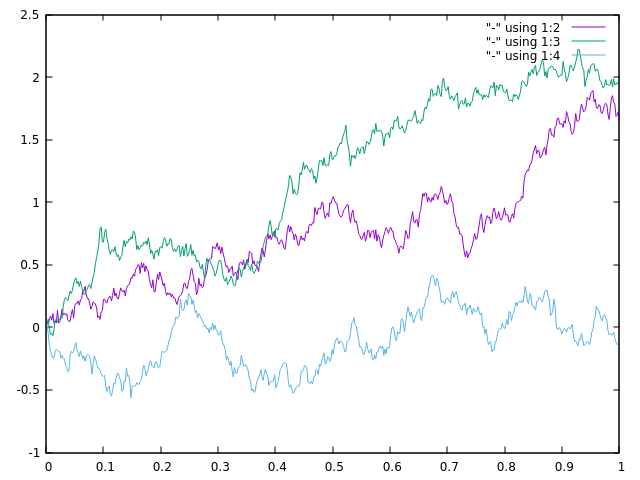
Самое время перепроверить наши предыдущие вычисления. Давайте посчитаем вариацию траектории Броуновского движения на интервале $inline$ .

Prelude> totalVariation (brownianMotion 1 100 1)
8.167687948236862
Prelude> totalVariation (brownianMotion 1 10000 1)
80.5450335433388
Prelude> totalVariation (brownianMotion 1 1000000 1)
798.2689137110999

Мы можем наблюдать, что при увеличении точности вариация принимает все большие и большие значения, в то время как квадратичная вариация стремится к $inline$ :

Prelude> quadraticVariation (brownianMotion 1 100 1)
0.9984487348804609
Prelude> quadraticVariation (brownianMotion 1 10000 1)
1.0136583395467458
Prelude> quadraticVariation (brownianMotion 1 1000000 1)
1.0010717246843375

Попробуйте позапускать вычисления вариаций для произвольных интегралов Ито, чтобы убедиться в том, что $[I](h) = \int_0^T h^2(s)ds$ вне зависимости от траектории движения.

Мартингалы

Есть такой класс случайных процессов — мартингалы. Для того, чтобы $inline$ был мартингалом, необходимо выполнение трех условий:

Он адаптирован
$inline$ почти всюду конечно:
$\mathbb{E}[|X(t)|] < \infty$
Условное математическое ожидание будущего значения $inline$ равняется его последнему известному значению:
$\mathbb{E}[X(T)|X(t)] = X(t), \quad t < T.$

Броуновское движение — мартингал. Выполнение первого условия очевидно, выполнение второго условия следует из свойств нормального распределения. Третье условие также легко проверяется:

$\mathbb{E}[B(T)|B(t)] = \mathbb{E}[(B(T)-B(t)) + B(t)|B(t)] = B(t).$

Интеграл Ито тоже мартингал (оставим доказательство в качестве упражнения). О чем это нам говорит? Вернемся к финансовой математике и представим, что стоимость на выбранные нами акции — это Броуновское движение (предположение довольно наивное, но все же представим), а $inline$ — это наша стратегия, количество акций в нашем портфеле. Процесс $inline$ может быть случайным: мы не всегда знаем сильно заранее сколько акций мы захотим сохранить, будем исходить из движения цены $inline$ . Но главное, чтобы этот процесс был адаптирован, то есть на момент $inline$ мы точно знаем, сколько акций у нас лежит. Мы не можем вернуться в прошлое и поменять это значение. Так вот, так как интеграл Ито — это мартингал, то абсолютно неважно какой мы выберем стратегию $inline$ , в среднем выигрыш от нашей торговли всегда будет уходить в ноль.

Есть еще одна интересная теорема, так называемая теорема о представлении мартингала: если у нас есть мартингал $inline$ , чьи значения определяются Броуновским движением, то есть единственный процесс, вносящий неопределенность в значения $inline$ , — это $inline$ , то этот мартингал можно представить в виде

$M(t) = M(0) + \int_0^t H(s)dB(s),$

притом процесс $inline$ единственен. В дальнейшем, когда мы увеличим количество интегралов и даже расширим их на неадаптированные процессы, эта теорема нам очень поможет.

А на сегодня всё.

Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.

Стоит ли рассказать про лемму Ито-Деблина?

95.93% Да, определенно стоит!118

4.07% Нет, это всё не формат Хабра5

Проголосовали 123 пользователя. Воздержались 25 пользователей.

Теги:

Хабы:

О фракталах, мартингалах и случайных интегралах. Часть первая

Скрытая угроза фракталов

Бесконечная вариация Броуновского движения

Интеграл Ито или Новая надежда

Интеграл Ито для простых процессов

Интеграл Ито для сложных процессов

Покодим?

Мартингалы

Публикации

Ближайшие события