Комментарии 19
Отличное видео про визуализацию пифагорских троек Думаю в данном случае можно найти похожее обобщенное решение
Таким образом можно взять любое x, разложить на любые два множителя число
и ответом будет тройка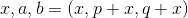 
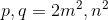, где n — нечетно.Таким образом для некратных решений получаем ответ
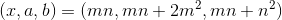, где 2m и n взаимно просты, который совпадает с ответом автора.
a = x + (2*x*x)/(b-x)
Моему далекому от Бурбакизма мозгу проще оперировать геометрическими кустарными аналогиями, чем производить формальные символьно-алгебраические преобразования без бумажки. Поэтому (в обозначениях автора) я бы вырезал правый нижний кусок (удалил 2 одинаковых куска разного цвета) и получил бы (заменив разность в-х например с)
сх + 2хх = са = с(х+щ) (о Боже, мозг, ну зачем ты выбрал щ? наверное потому что так проще набирать не переключая раскладку?)
откуда со всей очевидностью выходим на сокровенную формулу 2хх = сщ, где задавая любой х можем получить все варианты через факторизацию.
Та же кустарщина с Пифагоровыми тройками: впишем мелкий целочисленный квадрат в угол большого, останется "уголок", из которого тоже должно быть можно сложить полный квадрат. То есть отрезав от каждой "ноги" уголка хвостики, ими можно было заполнить оставшееся пустое место обрезанного уголка до квадрата. При ширине "ноги" х и пропорции отрезания а к б получаем (сразу безо всякой алгебры) волшебную формулу:
аа = 2бх, что очень похоже на волшебную формулу выше. И так же берем любой четный (по очевидным причинам) полный квадрат (а следовательно четное а), факторизуем его и получаем все тройки, задаваемые данным а. Например:
а = 2: б = 2, х = 1 — переводя к Пифагору м = а + б = 4, н = а + х = 3, к = а + б + х = 5
или
а = 100: бх = 5000, пусть б = 5, х = 1000; тогда м = 105, н = 1100, к = 1105 и т.д., т.е. каждое четное а принесет нам пачку троек. хотя в данном случае тройка получилась кратная, можно сократить на 5 — но если надо отсекать кратные тройки можно предварительно факторизовать а и не группировать в б и х одинаковые составляющие
Из дальнейших попыток поиграться с сабжевой задачей варианты с добавлением такой же площади если приклеивать желтые куски одинаковой ширины с 3 или 4 сторон приводят к тривиальным (не настолько интересным) уравнениям, вариант достройки прямоугольника до квадрата в 2 раза большей площади приводит к ровно такому же сид эквэйшену, как и для Пифагоровых троек, а вариант как у автора, только чтобы желтая площадь была в 2 раза меньше синей решается аналогичными кустарными рассуждениями, приводящими к сид (как это по-русски?) уравнению вида:
6хх = сщ где а = щ + 2х, б = с + 2х
например при х = 1 беря с = 3 и щ = 2 получаем а = 4, б = 5 и синяя площадь аб = 20 а желтая площадь (а+х)(б+х) — аб = 30 — 20 = 10 и в 2 раза меньше синей.
Похоже, что целый класс задач сводится к сид эквэйшенам подобного простого вида.
Мозаика в ванной и диофантовы уравнения