Привет, Хабр. Сегодня я бы хотел развить тему вариационной оптимизации и рассказать, как применить её к задаче обрезки малоинформативных каналов в нейронных сетях (pruning). При помощи неё можно сравнительно просто увеличить «скорострельность» нейронной сети, не перелопачивая её архитектуру.

Идея редукции лишних элементов в алгоритмах машинного обучения совсем не нова. На самом деле, она старее чем понятие deep learning: только раньше резали ветви решающих деревьев, а сейчас веса в нейронной сети.
Основная мысль проста: мы находим в сети подмножество бесполезных весов и обнуляем их. Без полного перебора сложно сказать, какие веса по-настоящему участвуют в предсказании, а какие только притворяются, но это и не требуется. Недурно работают различные методы регуляризации, Optimal Brain Damage и другие алгоритмы. Зачем же вообще удалять какие-либо веса? Оказывается, что это улучшает обобщающую способность сети: как правило, малозначимые веса либо просто вносят шум в предсказание, либо специально заточены на признаки тренировочного датасета (т.е. артефакт переобучения). В этом смысле редукцию связей можно сравнить с методом отключения случайных нейронов (dropout) во время тренировки сети. Кроме того, если в сети много нулей, она занимает меньше места в архиве и способна быстрее считаться на некоторых архитектурах.
Звучит неплохо, но гораздо интереснее выкидывать не отдельные веса, а нейроны из полносвязных слоёв или каналы из свёрток целиком. В этом случае эффек�� сжатия сети и ускорения предсказаний наблюдается намного более явно. Но это сложнее, чем уничтожение отдельных весов: если попытаться провести Optimal Brain Damage, взяв вместо одной связи всю пачку, результаты скорее всего окажутся не очень впечатляющими. Чтобы можно было безболезненно удалить нейрон, нужно специально сделать так, чтобы у него не было ни одной полезной связи. Для этого нужно как-то побудить «сильные» нейроны становиться сильнее, а «слабые» — слабее. Эта задача нам уже знакома: по сути мы заставляем сеть быть разреженной (sparsity inducing) с некоторыми ограничениями на группировку весов.

Обратите внимание, что для удаления одного нейрона или свёрточного канала, нужно модифицировать две матрицы весов. Я не буду делать различий между свёрточными каналами и нейронами: работа с ними одинакова, отличаются лишь конкретные удаляемые веса и способ транспонирования.
Для начала расскажу про наиболее простой и эффективный способ изъятия лишних нейронов из сети — групповую LASSO-регуляризацию. Чаще всего именно её применяют, чтобы держать бесполезные веса в сетях близко к нулю; она тривиально обобщается на поканальный случай. В отличие от обычной регуляризации, мы не регуляризируем веса или активации слоя напрямую, идея чуть-чуть хитрее. [Channel Pruning for Accelerating Very Deep Neural Networks; Yihui He et al; 2017]

Рассмотрим специальный маскирующий слой с вектором весов . Его вывод — просто поэлементное произведение
. Его вывод — просто поэлементное произведение  на выводы предыдущего слоя, активационной функции у него нет. Поместим по маскирующему слою после каждого слоя, каналы в котором хотим отбрасывать, и подвергнем веса в этих слоях L1-регуляризации. Таким образом вес маски
на выводы предыдущего слоя, активационной функции у него нет. Поместим по маскирующему слою после каждого слоя, каналы в котором хотим отбрасывать, и подвергнем веса в этих слоях L1-регуляризации. Таким образом вес маски  , умножающийся на i-тый вывод слоя неявно налагает ограничение на все веса, от которых зависит этот вывод. Если среди этих весов, скажем половина полезных, то
, умножающийся на i-тый вывод слоя неявно налагает ограничение на все веса, от которых зависит этот вывод. Если среди этих весов, скажем половина полезных, то  будет держаться ближе к единице, и этот вывод сможет хорошо передавать информацию. Но если только один или вовсе ни одного,
будет держаться ближе к единице, и этот вывод сможет хорошо передавать информацию. Но если только один или вовсе ни одного,  упадёт до нуля, что обнулит вывод нейрона и, по сути, обнулит все веса, от которых зависит этот вывод (в случае активационной функции равной нулю в нуле). Обратите внимание, что таким образом сеть получает меньше негативного подкрепления в случае законно больших весов, или законно сильного отклика. Имеет значение полезность нейрона в целом.
упадёт до нуля, что обнулит вывод нейрона и, по сути, обнулит все веса, от которых зависит этот вывод (в случае активационной функции равной нулю в нуле). Обратите внимание, что таким образом сеть получает меньше негативного подкрепления в случае законно больших весов, или законно сильного отклика. Имеет значение полезность нейрона в целом.
Получается вот такая формула:
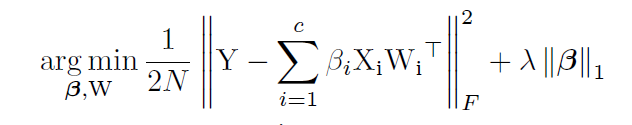
Где — константа взвешивания loss'a сети и loss'a разреженности. Похоже на обычную формулу L1-регуляризации, только во втором члене содержатся вектора маскирующих слоёв, а не веса сети.
— константа взвешивания loss'a сети и loss'a разреженности. Похоже на обычную формулу L1-регуляризации, только во втором члене содержатся вектора маскирующих слоёв, а не веса сети.
После окончания обучения сети мы пробегаемся по нейронам и маскирующим их значениям. Если больше определённого порога, то веса нейрона умножаются на
больше определённого порога, то веса нейрона умножаются на  , если меньше, то из матриц входящих и исходящих весов удаляются соответствующие нейрону элементы (как на картинке немного выше). После этого маски можно отбросить и доучить сеть.
, если меньше, то из матриц входящих и исходящих весов удаляются соответствующие нейрону элементы (как на картинке немного выше). После этого маски можно отбросить и доучить сеть.
В применении групповой LASSO есть несколько тонкостей:
Но мы же не ищем лёгких путей, правда?
Отбраковка каналов при помощи L1-регуляризации не совсем честна. Она позволяет каналу перемещаться по шкале «сильный отклик» — «слабый отклик» — «нулевой отклик». Только когда маскирующий вес оказывается достаточно близок к нулю, мы отбрасываем канал при помощи маски захвата. Такое перемещение здорово искажает картину и вносит изменения в другие каналы во время тренировки: прежде чем они смогут выучить, что делать, когда предыдущий нейрон полностью отключён, они должны выучить, что делать, когда он систематически даёт слабый отклик.
Напомню, что в идеале нам бы хотелось жадным образом выбрать наименее информативный канал из сети, продолжить учить сеть без него, удалить следующий наименее информативный канал, снова подстроить сеть и так далее. Увы, в такой постановке задача вычислительно неподъёмна даже для сравнительно простых сетей. К тому же такой подход не оставляет каналам второго шанса — единожды удалённый нейрон не снова может вернуться в строй. Немного изменим задачу: будем иногда удалять нейрон, а иногда оставлять. Притом, если нейрон в целом полезный, чаще оставлять, а если бесполезный — наоборот. Для этого будем использовать такие же маскирующие слои, как в случае L1-регуляризации (не зря же их вводили!). Только их веса будут не перемещаться по всей действительной оси с атт��актором в нуле, а будут сконцентрированы вокруг 0 и 1. Не то чтобы стало сильно проще, но по крайней мере разобрались с проблемой категоричности удаления нейронов.
Инстинкт обучатора сетей подсказывает, что не стоит решать задачу перебором, а нужно добавить количество активных нейронов в слоях на текущем прогоне в функцию потерь. Однако такой член в loss'е будет ступенчато-постоянным, и градиентный спуск не сможет с ним работать. Нужно как-то научить алгоритм обучения периодически исключать некоторые нейроны, несмотря на отсутствие градиента.
У нас есть способ временно удалять нейроны: мы можем применить dropout к маскирующему слою. Пусть во время обучения с вероятностью
с вероятностью  и
и  с вероятностью
с вероятностью  . Теперь в функцию потерь можно поместить сумму
. Теперь в функцию потерь можно поместить сумму  , которая является действительным число. Здесь мы сталкиваемся с очередным препятствием: распределение-то дискретно, непонятно, как с ним работать backpropagation'у. Вообще существуют специальные алгоритмы оптимизации, которые могут нам здесь помочь (см. REINFORCE), но мы предпримем другой подход.
, которая является действительным число. Здесь мы сталкиваемся с очередным препятствием: распределение-то дискретно, непонятно, как с ним работать backpropagation'у. Вообще существуют специальные алгоритмы оптимизации, которые могут нам здесь помочь (см. REINFORCE), но мы предпримем другой подход.
Тут-то и настал момент, где в дело вступает вариацонная оптимизация: мы можем приблизить дискретное распределение нулей и единиц в маскирующем слое непрерывным и оптимизировать параметры последнего при помощи обычного алгоритма обратного распространения. В этом и состоит идея работы [Learning Sparse Neural Networks Through L0 Regularization; Christos Louizos et al; 2017].
Роль непрерывного распределения будет исполнять hard concrete distribution [The Concrete Distribution: A Continuous Relaxation of Discrete Random Variables; Chris Maddison; 2017], вот такая хитрая штука из логарифмов, приближающая распределение Бернулли:
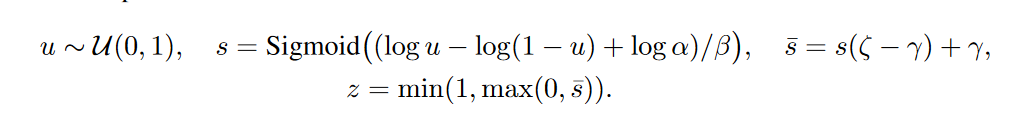
 — смещение распределение относительно центра, а
— смещение распределение относительно центра, а  — температура. При
— температура. При  распределение всё больше начинает приближать истинное распределение Бернулли, но теряет дифференцируемость. При
распределение всё больше начинает приближать истинное распределение Бернулли, но теряет дифференцируемость. При  плотность распределения вогнута (это интересующий нас случай), при
плотность распределения вогнута (это интересующий нас случай), при  — выпукла. Мы пропускаем это распределение через жёсткую сигмоиду, чтобы оно с конечной ненулевоей вероятностью умело выдавать
— выпукла. Мы пропускаем это распределение через жёсткую сигмоиду, чтобы оно с конечной ненулевоей вероятностью умело выдавать  и
и  , а на интервале (0, 1) облада��о непрерывной дифференцируемой плотностью. После окончания pruning'a мы смотрим в какую сторону сместилось распределение и заменяем случайную переменную
, а на интервале (0, 1) облада��о непрерывной дифференцируемой плотностью. После окончания pruning'a мы смотрим в какую сторону сместилось распределение и заменяем случайную переменную  на конкретное значение маски
на конкретное значение маски  и доводим до кондиции уже детерминированную модель.
и доводим до кондиции уже детерминированную модель.
Чтобы чуть лучше почувствовать распределение, приведу несколько примеров его плотности для разных параметров:
По сути у нас получился «умный» dropout-слой, который выучивает, какие выводы нужно чаще выбрасывать. Но что же конкретно мы оптимизируем? В loss следует поместить интеграл от плотности распределения в ненулевой области (вероятность, что маска окажется равной не нулю во время тренировки проще говоря):

К двухтактному обучению, обычной регуляризации и прочим подробностям имплементации упомянутым в главе про L1-регуляризацию добавляются следующие особенности:
Для эксперимента возьмём датасет CIFAR-10 и сравнительно простую сеть в четыре свёрточных слоя, за которыми следуют два полносвязных: Conv2D, Mask, Conv2D, Mask, Pool2D, Conv2D, Mask, Conv2D, Mask, Pool2D, Flatten, Dropout (p=0.5), Dense, Mask, Dense (logits). Считается, что алгоритмы pruning'а лучше работают на более «толстых» сетях, но тут я столкнулся с чисто технической проблемой недостатка вычислительных мощностей. В качестве оптимизатора использовался Adam с learning rate = 0.0015 и batch size = 32. Дополнительно использовались обычные L1 (0.00005) и L2 (0.00025) регуляризации. Image augmentation не применялся. Сеть обучалась 200 эпох до схождения, после чего сохранялась, и к ней применялись алгоритмы редукции нейронов.
Кроме применения для pruning'a алгоритмов, описанных выше, установим тривиальную отсчётная точку, чтобы убедиться, что алгоритмы вообще что-то делают. Попробуем попеременно выкидывать из каждого слоя первых нейронов и доучивать получившуюся сеть.
нейронов и доучивать получившуюся сеть.
На графике представлены результаты сравнения L1 и L0 алгоритмов редукции каналов после серии экспериментов с разными константами мощности регуляризации. По оси X отложено уменьшение количества весов в процентах после применения алгоритма. По оси Y — точность порезаной сети на валидационной выборке. Синяя полоса посередине — примерное качество сети, ещё не подвергнутой вырезанию нейронов. Зелёная линия представляет простой алгоритм L1-обучения масок. Красная линия — L0-pruning. Фиолетовая линия — удаление первых каналов. Чёрные треугольники — обучение сети, у которой изначально было меньшее количество весов.
каналов. Чёрные треугольники — обучение сети, у которой изначально было меньшее количество весов.

Ещё один пример для CIFAR-100 и чуть более длинной и широкой сети примерно такой же архитектуры и с похожими параметрами обучения:

Ииии на графиках хорошо видно, что простой L1-алгоритм справляется ничуть не хуже хитрой вариационной оптимизации, и как будто бы даже чуть больше улучшает качество сети при малых значениях компрессии. Результаты также подтверждаются разовыми экспериментами с другими датасетами и архитектурами сетей. Это абсолютно ожидаемый результат, на который я и рассчитывал, когда начинал эксперименты над редукцией сетей. Честно. Sigh.
Ну ладно, если честно, я был слегка удивлён, и пробовал играться с алгоритмом и сетью: разные архитектуры, гиперпараметры сети, точные формулы hard concrete distribution, начальные значения и
и  , количество эпох промежуточной подстройки. Выглядит L0-регуляризация в теории круто, но на практике для неё сложнее подобрать гиперпараметры, и считается она дольше, так что я бы не советовал применять её без дополнительных экспериментов и обработки напильником. Пожалуйста, не считайте потраченным время на чтение статьи: L0-pruning выглядит действительно очень правдоподобно, и я бы сказал, что скорее я где-то неправильно применил алгоритм, что не получил обещанного прироста. Плюс, вариационная оптимизация является основой для ещё более продвинутых алгоритмов редукции [например, Compressing Neural Networks using the Variational
, количество эпох промежуточной подстройки. Выглядит L0-регуляризация в теории круто, но на практике для неё сложнее подобрать гиперпараметры, и считается она дольше, так что я бы не советовал применять её без дополнительных экспериментов и обработки напильником. Пожалуйста, не считайте потраченным время на чтение статьи: L0-pruning выглядит действительно очень правдоподобно, и я бы сказал, что скорее я где-то неправильно применил алгоритм, что не получил обещанного прироста. Плюс, вариационная оптимизация является основой для ещё более продвинутых алгоритмов редукции [например, Compressing Neural Networks using the Variational
Information Bottleneck, 2018].
В целом можно сделать следующие выводы:
Помните, как я в начале поста написал, что после завершения алгоритма прунинга можно «просто вырезать лишние куски сети целиком»? Так вот, вырезать лишние куски сети совсем не просто. Tensorflow и прочие библиотеки строят вычислительный граф, и его нельзя так просто изменить, когда он уже в работе. Приходится сохранять сеть с вычисленными масками, выдирать из неё список нужных весов, транспонировать веса нужным образом, удалять обнулённые группы, транспонировать обратно, и создавать новую сеть на основе выходного набора тензоров. Получившаяся сеть должна обладать такой же планировкой, как и исходная, но в ней будет меньше нейронов. Ожидайте головную боль с поддерживанием одинаковой схемы сети в функции создания изначальной и финальной сети, особенно, если они не линейные, а ветвистые.
Вероятно для удобного маскирования придётся создавать свои слои. Это несложно, но будьте внимательны, в какие коллекции вы добавляете параметры маскрирования. Тут несложно ошибиться и случайно тренировать параметры редукции каналов вместе со всеми остальными весами.
Следует заметить, что заметная часть весов сетей с не очень глубокими архитектурами обычно сконцентрирована на переходе из свёрточной части в полносвязную. Так происходит из-за того что последний свёрточный слой делается плоским, вследствие чего в нём как бы образуется (количество каналов)*(ширина)*(высота) нейронов, и следующая матрица весов получается очень широкой. Эти веса вряд ли получится порезать; более того этого не надо делать, иначе последние слои сети окажутся «слепы» к фичам, найденным в некоторых местах. Старайтесь в таких случаях делать финальное количество каналов меньшим и пользоваться maxpool'ингом или вовсе использовать полностью свёрточные или полностью полносвязные архитектуры.
Всем спасибо за внимание, если кому-то интересно повторить эксперименты над CIFAR-10 и CIFAR-100, код можно взять на гитхабе. Хорошего рабочего дня!

Идея редукции лишних элементов в алгоритмах машинного обучения совсем не нова. На самом деле, она старее чем понятие deep learning: только раньше резали ветви решающих деревьев, а сейчас веса в нейронной сети.
Основная мысль проста: мы находим в сети подмножество бесполезных весов и обнуляем их. Без полного перебора сложно сказать, какие веса по-настоящему участвуют в предсказании, а какие только притворяются, но это и не требуется. Недурно работают различные методы регуляризации, Optimal Brain Damage и другие алгоритмы. Зачем же вообще удалять какие-либо веса? Оказывается, что это улучшает обобщающую способность сети: как правило, малозначимые веса либо просто вносят шум в предсказание, либо специально заточены на признаки тренировочного датасета (т.е. артефакт переобучения). В этом смысле редукцию связей можно сравнить с методом отключения случайных нейронов (dropout) во время тренировки сети. Кроме того, если в сети много нулей, она занимает меньше места в архиве и способна быстрее считаться на некоторых архитектурах.
Звучит неплохо, но гораздо интереснее выкидывать не отдельные веса, а нейроны из полносвязных слоёв или каналы из свёрток целиком. В этом случае эффек�� сжатия сети и ускорения предсказаний наблюдается намного более явно. Но это сложнее, чем уничтожение отдельных весов: если попытаться провести Optimal Brain Damage, взяв вместо одной связи всю пачку, результаты скорее всего окажутся не очень впечатляющими. Чтобы можно было безболезненно удалить нейрон, нужно специально сделать так, чтобы у него не было ни одной полезной связи. Для этого нужно как-то побудить «сильные» нейроны становиться сильнее, а «слабые» — слабее. Эта задача нам уже знакома: по сути мы заставляем сеть быть разреженной (sparsity inducing) с некоторыми ограничениями на группировку весов.

Обратите внимание, что для удаления одного нейрона или свёрточного канала, нужно модифицировать две матрицы весов. Я не буду делать различий между свёрточными каналами и нейронами: работа с ними одинакова, отличаются лишь конкретные удаляемые веса и способ транспонирования.
Простой способ: групповая L1-регуляризация
Для начала расскажу про наиболее простой и эффективный способ изъятия лишних нейронов из сети — групповую LASSO-регуляризацию. Чаще всего именно её применяют, чтобы держать бесполезные веса в сетях близко к нулю; она тривиально обобщается на поканальный случай. В отличие от обычной регуляризации, мы не регуляризируем веса или активации слоя напрямую, идея чуть-чуть хитрее. [Channel Pruning for Accelerating Very Deep Neural Networks; Yihui He et al; 2017]

Рассмотрим специальный маскирующий слой с вектором весов
Получается вот такая формула:
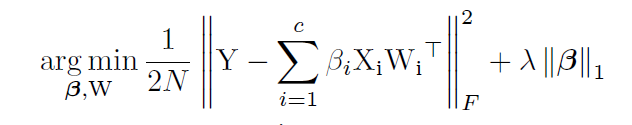
Где
После окончания обучения сети мы пробегаемся по нейронам и маскирующим их значениям. Если
В применении групповой LASSO есть несколько тонкостей:
- Обычная регуляризация. Вкупе с регуляризацией маскирующих весов следует применять L1/L2 регуляризацию и ко всем остальным весам сети. Без этого уменьшение маскирующего веса в случае ненасыщаемых активационных функций (ReLu, ELu) будет запросто компенсировано увеличением весов, и обнуляющего эффекта не выйдет. Да и для обычных сигмоид это позволяет лучше запустить процесс с положительной обратной связью:
малоинформативного вывода становится меньше, из-за чего оптимизатору приходится сильнее задуматься над каждым конкретным весом, из-за чего вывод становится ещё более малоинформативным, из-за чего
уменьшается ещё больше и так далее.
- Авторы статьи также советуют накладывать сферическое ограничение на веса слоёв
. Вероятно, это должно поспособствовать «перетеканию» весов от слабых нейронов к сильным, но я не заметил особой разницы.
- Двухтактное обучение. Авторы статьи предлагают попеременно обучать обычные веса нейронной сети и маскирующие веса. Это дольше, чем обучать всё за раз, но как будто бы результаты чуть лучше?
- Не забывайте про длительную точную подстройку сети (fine-tuning) после фиксации маски, это очень важно.
- Внимательно следите, как у вас стоят маски: до или после функции активации. У вас могут быть проблемы с активациями, которые не равняются нулю при аргументе равном нулю (например, сигмоида).
- Pruning не дружит с batchnorm примерно по той же причине, по которой с ним не дружит dropout: с точки зрения нормализации, когда в пачке 32 значения из которых 12 нулевые, и когда в пачке 20 значений — это очень разные ситуации. После выдирания обнулённых весов распределение, выученное batchnorm слоем перестаёт быть валидным. Нужно либо вставлять pruning-слои после всех batchnorm-слоёв, либо как-то модифицировать последние.
- Также есть сложности с применением редукции каналов к «ветвистым» архитектурам и residual-сетям (ResNet). После обрезки лишних нейронов во время слияния ветвей могут не совпасть размерности. Это легко решается введением буферных слоёв, нейроны в которых мы не отбраковываем. Кроме того, если ветви сети несут разное количество информации, имеет смысл установить для них разный
, чтобы не оказалось, что Pruning просто порезал все нейроны в наименее информативной ветви. Впрочем, если все нейроны порезались, то не так уж ветвь и важна?
- В оригинальной постановке задачи указано жёсткое ограничение на количество ненулевых каналов, но на мой взгляд тут достаточно менять лишь параметра взвешивания изначального loss'а и L1-loss'а маскирующих весов, а дальше пусть сам оптимизатор решает, сколько каналов оставлять.
- Маски захвата. Этого нет в оригинальной статье, но на мой взгляд, это хороший практический механизм для улучшения сходимости. Когда значение маски достигает некоторого заранее заданного низкого значения, мы обнуляем его и запрещаем менять эту часть маски. Таким образом слабые веса полностью перестают вносить вклад в предсказание уже во время тренировки модели, а не вносят в соответствующие суммы какие-то паразитные значения. Теоретически это может помешать потенциально полезному каналу вернуться в строй, но не думаю, что такое происходит на практике.
Сложный способ: L0-регуляризация
Но мы же не ищем лёгких путей, правда?
Отбраковка каналов при помощи L1-регуляризации не совсем честна. Она позволяет каналу перемещаться по шкале «сильный отклик» — «слабый отклик» — «нулевой отклик». Только когда маскирующий вес оказывается достаточно близок к нулю, мы отбрасываем канал при помощи маски захвата. Такое перемещение здорово искажает картину и вносит изменения в другие каналы во время тренировки: прежде чем они смогут выучить, что делать, когда предыдущий нейрон полностью отключён, они должны выучить, что делать, когда он систематически даёт слабый отклик.
Напомню, что в идеале нам бы хотелось жадным образом выбрать наименее информативный канал из сети, продолжить учить сеть без него, удалить следующий наименее информативный канал, снова подстроить сеть и так далее. Увы, в такой постановке задача вычислительно неподъёмна даже для сравнительно простых сетей. К тому же такой подход не оставляет каналам второго шанса — единожды удалённый нейрон не снова может вернуться в строй. Немного изменим задачу: будем иногда удалять нейрон, а иногда оставлять. Притом, если нейрон в целом полезный, чаще оставлять, а если бесполезный — наоборот. Для этого будем использовать такие же маскирующие слои, как в случае L1-регуляризации (не зря же их вводили!). Только их веса будут не перемещаться по всей действительной оси с атт��актором в нуле, а будут сконцентрированы вокруг 0 и 1. Не то чтобы стало сильно проще, но по крайней мере разобрались с проблемой категоричности удаления нейронов.
Инстинкт обучатора сетей подсказывает, что не стоит решать задачу перебором, а нужно добавить количество активных нейронов в слоях на текущем прогоне в функцию потерь. Однако такой член в loss'е будет ступенчато-постоянным, и градиентный спуск не сможет с ним работать. Нужно как-то научить алгоритм обучения периодически исключать некоторые нейроны, несмотря на отсутствие градиента.
У нас есть способ временно удалять нейроны: мы можем применить dropout к маскирующему слою. Пусть во время обучения
Тут-то и настал момент, где в дело вступает вариацонная оптимизация: мы можем приблизить дискретное распределение нулей и единиц в маскирующем слое непрерывным и оптимизировать параметры последнего при помощи обычного алгоритма обратного распространения. В этом и состоит идея работы [Learning Sparse Neural Networks Through L0 Regularization; Christos Louizos et al; 2017].
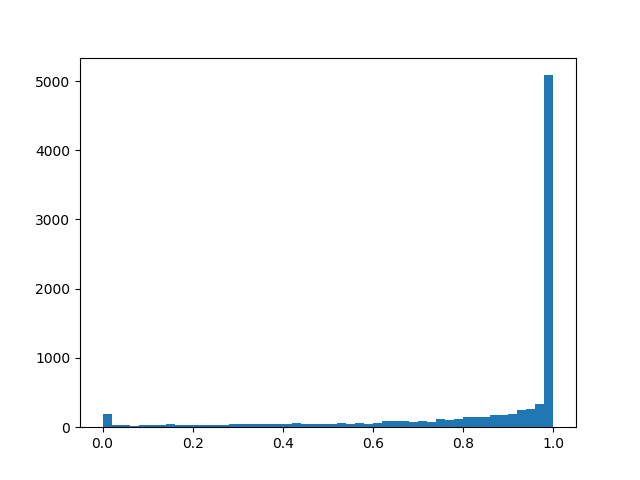
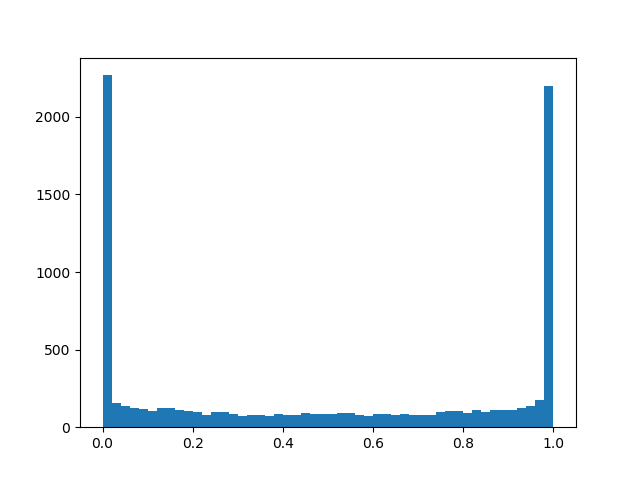
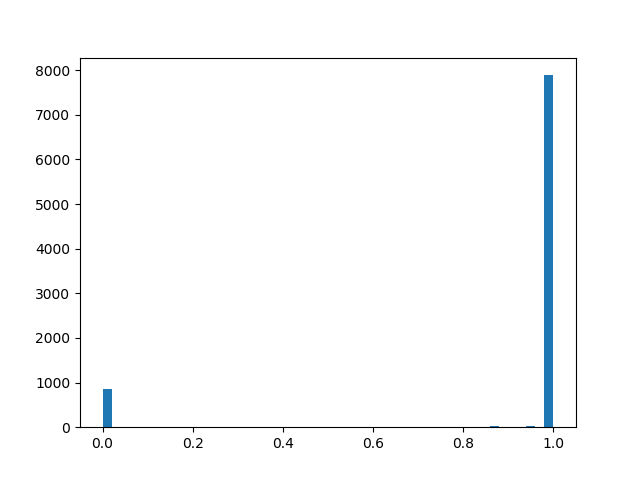
Роль непрерывного распределения будет исполнять hard concrete distribution [The Concrete Distribution: A Continuous Relaxation of Discrete Random Variables; Chris Maddison; 2017], вот такая хитрая штука из логарифмов, приближающая распределение Бернулли:
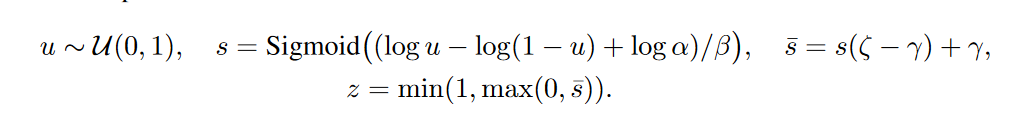
Чтобы чуть лучше почувствовать распределение, приведу несколько примеров его плотности для разных параметров:
Плотность распределения :
:

 :
:

 :
:
 :
:
 :
:

 :
:

 :
:
 :
:









По сути у нас получился «умный» dropout-слой, который выучивает, какие выводы нужно чаще выбрасывать. Но что же конкретно мы оптимизируем? В loss следует поместить интеграл от плотности распределения в ненулевой области (вероятность, что маска окажется равной не нулю во время тренировки проще говоря):

К двухтактному обучению, обычной регуляризации и прочим подробностям имплементации упомянутым в главе про L1-регуляризацию добавляются следующие особенности:
- Ещё раз: наш «умны»й dropout-слой с некоторой заметной вероятностью обнуляет выход, с некоторой — оставляет как есть, и плюс, есть небольшой шанс, зависящий от
, что вывод будет умножен на случайное число от 0 до 1. Последняя часть скорее паразитная чем полезная для нашей конечной цели, но без неё никак — она нужна для обратного прохода backpropagation'a.
- Вообще и
и
— тренируемые параметры, но в своих экспериментах я почувствовал, что если просто задать маленькую
(0.05) и в процессе обучения её ещё линейно уменьшать, то алгоритм сходится лучше, чем если её честно выучивать.
лучше задать достаточно большую
, чтобы изначально нейроны чаще сохранялись, чем отбрасывались, но недостаточно большую, чтобы насытилась сигмоида в loss'e.
- Если заменить в формулах
на просто
как будто бы сеть лучше сходится и меньше шансов нарваться на NaN во время тренировки. При таком манёвре нужно не забыть изменить член в функции потерь и инициализацию.
- Также если сжульничать и заменить обычную сигмоиду в loss'e на жёсткую с ограничениями по
, регуляризация будет лучше сходиться и действовать сильнее.
- К
и
можно дополнительно применить регуляризацию, чтобы ещё больше увеличить разреженность.
- После окончания тренировки следует бинаризировать полученные результаты и упорно дообучать сеть с детерминированной маской до выхода val accuracy на константу. В статье приводится более точная формула, по которой вывод нейрона можно сделать детерминированным во время валидации или для выпуска сети в релиз, но кажется, что к концу обучения
оказываются достаточно поляризованными, чтобы сработала и простая эвристика:
— маска 0,
— маска 1 (но это не точно). После перехода к детерминированным маскам вы увидите скачок качества. Не забывайте, что мы сюда обнулять веса пришли, и ниже определённого порога веса всё равно нужно заменять маскирующие веса на нули.
- Дополнительный плюс L0-подхода — маскирующие слои начинают работать как dropout, что вносит в сеть мощный регуляризирующий эффект. Но это палка о двух концах: если начинать обучение со слишком маленьким
, есть риск порушить предварительно обученную структуру сети.
Эксперименты
Для эксперимента возьмём датасет CIFAR-10 и сравнительно простую сеть в четыре свёрточных слоя, за которыми следуют два полносвязных: Conv2D, Mask, Conv2D, Mask, Pool2D, Conv2D, Mask, Conv2D, Mask, Pool2D, Flatten, Dropout (p=0.5), Dense, Mask, Dense (logits). Считается, что алгоритмы pruning'а лучше работают на более «толстых» сетях, но тут я столкнулся с чисто технической проблемой недостатка вычислительных мощностей. В качестве оптимизатора использовался Adam с learning rate = 0.0015 и batch size = 32. Дополнительно использовались обычные L1 (0.00005) и L2 (0.00025) регуляризации. Image augmentation не применялся. Сеть обучалась 200 эпох до схождения, после чего сохранялась, и к ней применялись алгоритмы редукции нейронов.
Кроме применения для pruning'a алгоритмов, описанных выше, установим тривиальную отсчётная точку, чтобы убедиться, что алгоритмы вообще что-то делают. Попробуем попеременно выкидывать из каждого слоя первых
На графике представлены результаты сравнения L1 и L0 алгоритмов редукции каналов после серии экспериментов с разными константами мощности регуляризации. По оси X отложено уменьшение количества весов в процентах после применения алгоритма. По оси Y — точность порезаной сети на валидационной выборке. Синяя полоса посередине — примерное качество сети, ещё не подвергнутой вырезанию нейронов. Зелёная линия представляет простой алгоритм L1-обучения масок. Красная линия — L0-pruning. Фиолетовая линия — удаление первых

Ещё один пример для CIFAR-100 и чуть более длинной и широкой сети примерно такой же архитектуры и с похожими параметрами обучения:

Ииии на графиках хорошо видно, что простой L1-алгоритм справляется ничуть не хуже хитрой вариационной оптимизации, и как будто бы даже чуть больше улучшает качество сети при малых значениях компрессии. Результаты также подтверждаются разовыми экспериментами с другими датасетами и архитектурами сетей. Это абсолютно ожидаемый результат, на который я и рассчитывал, когда начинал эксперименты над редукцией сетей. Честно. Sigh.
Ну ладно, если честно, я был слегка удивлён, и пробовал играться с алгоритмом и сетью: разные архитектуры, гиперпараметры сети, точные формулы hard concrete distribution, начальные значения
Information Bottleneck, 2018].
В целом можно сделать следующие выводы:
- Многие каналы в обученной сети явно избыточны. Даже при установке малой константы регуляризации маски легко достичь сокращения 30-50% весов. Но если изначально тренировать слишком «тонкую» сетку, сложно достичь хороших результатов. Это говорит в пользу благотворного влияния широких слоёв на целевую функцию сети и в пользу теории лотерейных билетов [The Lottery Ticket Hypothesis: Training Pruned Neural Networks, J. Frankle and M. Carbin, 2018] (чем больше нейронов, тем больше шансов, что хотя бы один из них инициализируется так, что сформирует хорошее правило).
- Если начать с широкой сети и понемногу выкидывать каналы с доучиванием, то сеть держится весьма неплохо. Но если выкинуть сразу слишком много весов без доучивания точность сети непоправимо ухудшится. Пластичность нейронов лучше себя проявляет, когда сеть близко к оптимальному состоянию?
- Хоть и нельзя уменьшать количество весов сколь угодно долго, в этом деле можно зайти на удивление далеко. Судя по научным статьям и моим экспериментам спад обычно начинается в районе 60-90% компрессии по весам. Хоть в моих экспериментах разрыв между кривыми алгоритмов редукции нейронов и кривыми выбрасывания первых
нейронов составил <7%, многие научные статьи рапортуют о гораздо большем превосходстве.
- Обратите внимание, что в случае несильной компрессии (<60%) алгоритмы редкции нейронов работают как регуляризаторы: точность на валидационной выборке после работы алгоритмы даже выше, чем изначальная!
- Кроме L1 и L0 были испробованы алгоритмы обрезки каналов по величине весов и среднему количеству нулей функции активации (APoZ), но они не представлены на графике, т.к. показали себя едва лучше, чем просто обнуление верхних
каналов.
- В статьях обычно тренируют сеть до упора, и только потом применяют к ней алгоритмы отсекания лишних нейронов. Делается это, я так понимаю, для чистоты эксперимента, и чтобы было видно, что качество сети несильно ухудшилось относительно точки отсчёта. Но если вы уже знаете архитектуру и базовую точность, с которой соревнуетесь, то предварительное обучение до выхода на планку как будто бы необязательно. Всё равно после начала работы алгоритма pruning'а веса очень здорово переколбашиваются, и изначально точность заметно падает. Можно натренировать сеть до более-менее вменяемого состояния, после чего одновременно обучать и очищать сеть.
Пару слов о технической стороне вопроса
Помните, как я в начале поста написал, что после завершения алгоритма прунинга можно «просто вырезать лишние куски сети целиком»? Так вот, вырезать лишние куски сети совсем не просто. Tensorflow и прочие библиотеки строят вычислительный граф, и его нельзя так просто изменить, когда он уже в работе. Приходится сохранять сеть с вычисленными масками, выдирать из неё список нужных весов, транспонировать веса нужным образом, удалять обнулённые группы, транспонировать обратно, и создавать новую сеть на основе выходного набора тензоров. Получившаяся сеть должна обладать такой же планировкой, как и исходная, но в ней будет меньше нейронов. Ожидайте головную боль с поддерживанием одинаковой схемы сети в функции создания изначальной и финальной сети, особенно, если они не линейные, а ветвистые.
Вероятно для удобного маскирования придётся создавать свои слои. Это несложно, но будьте внимательны, в какие коллекции вы добавляете параметры маскрирования. Тут несложно ошибиться и случайно тренировать параметры редукции каналов вместе со всеми остальными весами.
Следует заметить, что заметная часть весов сетей с не очень глубокими архитектурами обычно сконцентрирована на переходе из свёрточной части в полносвязную. Так происходит из-за того что последний свёрточный слой делается плоским, вследствие чего в нём как бы образуется (количество каналов)*(ширина)*(высота) нейронов, и следующая матрица весов получается очень широкой. Эти веса вряд ли получится порезать; более того этого не надо делать, иначе последние слои сети окажутся «слепы» к фичам, найденным в некоторых местах. Старайтесь в таких случаях делать финальное количество каналов меньшим и пользоваться maxpool'ингом или вовсе использовать полностью свёрточные или полностью полносвязные архитектуры.
Всем спасибо за внимание, если кому-то интересно повторить эксперименты над CIFAR-10 и CIFAR-100, код можно взять на гитхабе. Хорошего рабочего дня!
