При решении задач передачи данных через линии, представленные частотными характеристиками, применяются преобразования Фурье – перевод сигналов из временной области в частотную область и обратно. Среда МАТЛАБ имеет полный набор функций для решения подобных задач. В этой работе разобран пример вычисления в МАТЛАБ реакции сигнала прошедшего через линию, характеристика которой измерена на частотах, не совпадающих с частотой передачи данных. Надеюсь, что этот пример позволит легче разобраться с особенностями технологии преобразования сигналов в среде МАТЛАБ.
Необходимо определить изменение формы двоичного цифрового сигнала проходящего через фильтр и сигнальную линию. Сигнал задан амплитудой и скоростью передачи. Фильтр второго порядка, нормированный относительно частоты передачи данных, задан постоянными времени. Передаточная функция сигнальной линии представлена измеренной частотной характеристикой в комплексной форме.
Среда, используемая для вычисления и отображения данных – MATLAB R2015а.
В качестве примера исходных данных взяты следующие отношения, опубликованные на сайте www.StatEye.org для версии метода StatEye 3.0 GUI [1, 2, 3].
Скорость передачи данных bps = 10,3125 Гбит/с. Постоянные времени нормированного фильтра второго порядка совпадают, их обратная величина составляет ¾ частоты передачи данных. Сигнальная линия представлена частотной характеристикой. Измерение характеристики выполнено на частотах channel.f = 0,006495:0,0012475:20 ГГц. Заданное число точек дискретизации преобразования Фурье: points = 2^13.
На Рисунок 1 показаны передача данных, последовательность и результаты обработки данных, которые рассмотрены в этой работе. Переход из временной области в частотную область и обратно выполняется при помощи алгоритма Быстрого Преобразования Фурье (БПФ, FFT).

Рисунок 1. Канал передачи данных. Входной сигнал iSignal.Tx, выходной сигнал фильтра iSignal.Filter_out, выход сигнальной линии iSignal.Rx. Представленные на диаграмме характеристики рассмотрены ниже.
В этой работе основные вычисления выполнены в частотной области. Для этого, исходный сигнал из временной области переведен в частотную область с использованием преобразования Фурье, перемножением спектральных характеристик сигнала, фильтра и сигнальной линии найден выходной сигнал тракта, который из частотной области переведен во временную область обратным преобразованием Фурье.
Скорость передачи данных в два раза выше частоты, на которой происходит передача данных. Максимальная частота измеренной сигнальной линии max(channel.f) = 20 ГГц. На этой частоте можно передавать данные со скоростью 40 Гбит/с (как 2*max(channel.f)).
Максимальная скорость передачи данных, которая не превышает максимальную скорость передачи по сигнальной линии 40 Гбит/с и кратная скорости передачи bps = 10,3125 Гбит/с, равна fmax = 30,9375 Гбит/с, кратность N = 3 (N = fmax/bps). Далее, fmax используется как предельная частота для расчета реакции сигнала с применением преобразования Фурье.
Дискретность по времени для построения входного сигнала (бита данных) во временной области Ts = 1/fmax; Ts = 3,232e-11 с. Нормированная по отношению к длительности сигнала, временная шкала time состоит из 2^13 точек (points), шкала включает следующий массив точек time = bps/Ts .* (1:points). Дискретный единичный сигнал при скорости передачи bps = 10,3125 Гбит/с и квантовании с периодом Ts = 1/fmax состоит из трех точек в диапазоне от 10 до 11 единиц нормализованного времени. Сигнал единичной амплитуды можно построить и в любом другом месте временной шкалы, но лучше отступить с краев, чтобы полностью видеть предысторию и переходный процесс выходного сигнала. Импульсный сигнал (бит данных), построенный с использованием следующих команд МАТЛАБ, показан на Рисунок 2.
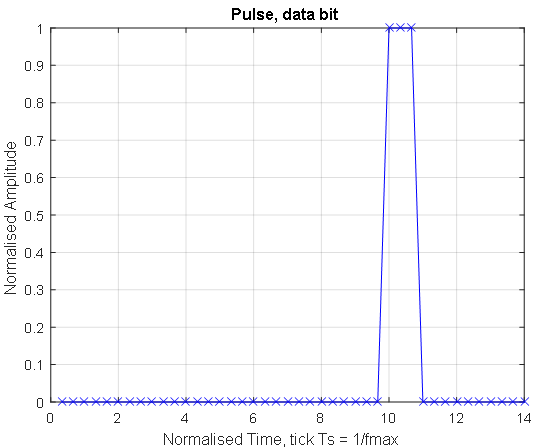
Рисунок 2. Входной импульсный сигнал iSignal.Tx, бит данных.
Перевод сигнала iSignal.Tx в частотную область выполняют следующие БПФ функции.
Функция преобразования Фурье fft строит симметричный спектр сигнала в областях положительных и отрицательных частот, максимальная частота которого находится в центре спектра (см. Рисунок 3). Функция fftshift восстана��ливает спектр, сдвигая в центр нулевую частоту сигнала как показано на Рисунок 4.
Разрешение частоты спектра равно fs = fmax/points; Частоты спектра лежат в диапазоне от -fmax/2 до fmax/2-fs и равны f = -fmax/2:fs:fmax/2-fs;
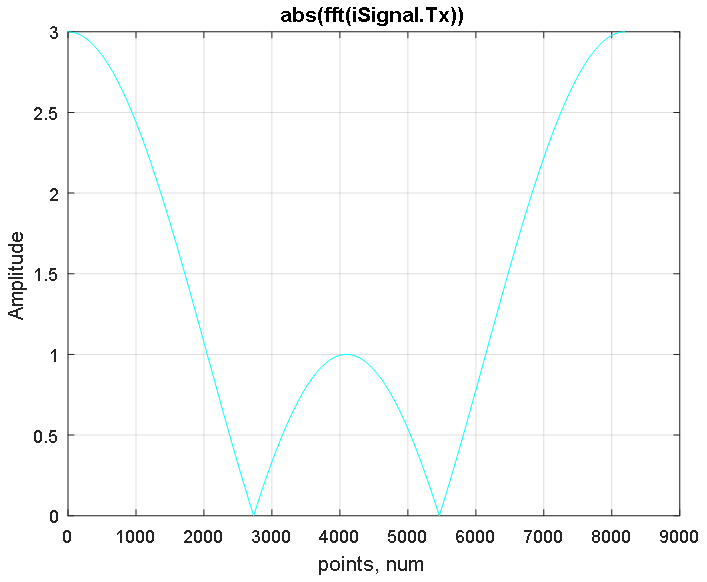
Рисунок 3. Амплитудная характеристика сдвинутого спектра сигнала iSignal.Tx полученного с использованием БПФ.
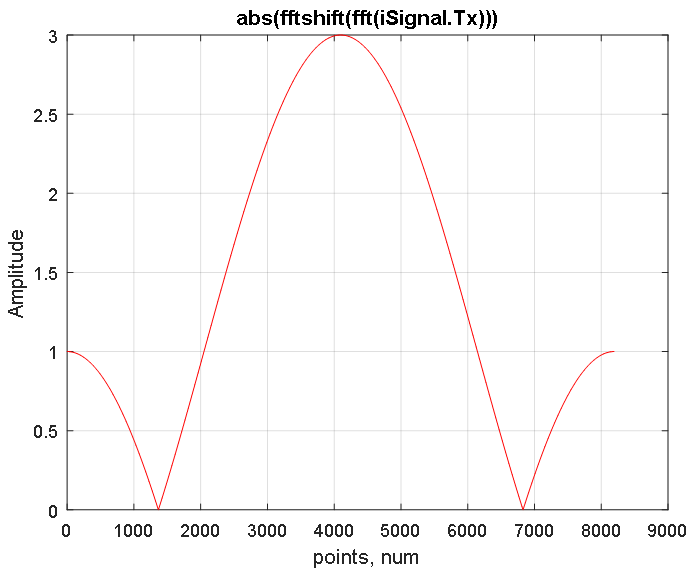
Рисунок 4. Амплитудная характеристика восстановленного спектра сигнала iSignal.Tx показанного на Рисунок 3. Представлено 2^13 отсчетов. Средний отсчет в точке 4097 соответствует нулевой частоте. В левой части (от 1 до 4096 точки) располагаются отрицательные частоты, в правой части (от 4098 до 8192 точки) – область положительных частот.
В этом примере передаточная функция фильтра второго порядка имеет вид
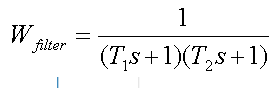
где Т1 и Т2 – постоянные времени фильтра. Значения частот 1/T1 равны и 1/T2 заданы относительно частоты, на которой передаются данные: 1/T1 = 1/T2 = 0,75*bps (bps = 10,3125 Гбит/с).
Полоса частот нормализованного фильтра
Оператор
Амплитудно-фазовая характеристика нормализованного фильтра для положительных и отрицательных частот нормализованных относительно частоты передачи сигнала показана на Рисунок 5. Логарифмическая амплитудно-частотная характеристика фильтра показана на Рисунок 6.
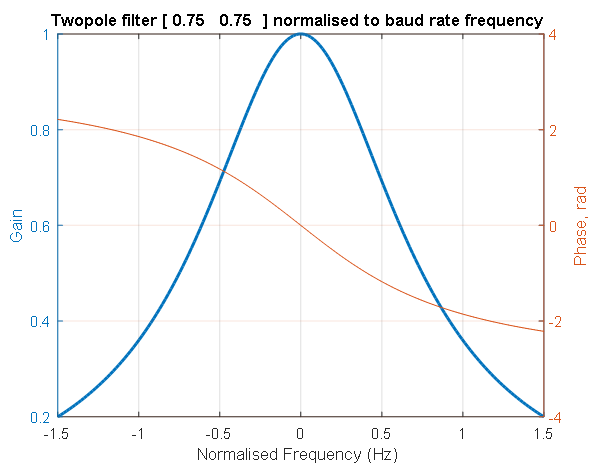
Рисунок 5. Амплитудно-фазовая характеристика нормализованного фильтра
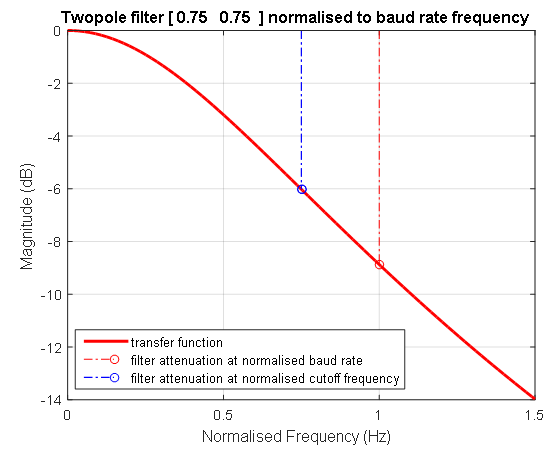
Рисунок 6. Логарифмическая амплитудно-фазовая частотная характеристика нормализованного фильтра. Синяя штриховая линия показывает положение частоты фильтра со значением 0,75 от частоты, на которой идет передача данных. На этой частоте (1/T1 = 1/T2) коэффициент передачи фильтра второго порядка равен -6 децибел. Красная штриховая линия показывает единичную частоту, на которой идет передача данных.
Измеренная амплитудно-фазовая характеристика сигнальной линии включает 1599 отсчетов в полосе до 20 ГГц с фиксированным шагом 12,475 МГц. Она содержит следующие значения частот: channel.f = 0,006495:0,0012475:20 ГГц. Изначально, сигнальная линия была представлена характеристикой четырехполюсника. Эта характеристика была преобразована и в примере используется в виде одномерной комплексной функции.
Частоты характеристики сигнальной линии, полученные в результате измерения, не совпадают с частотами спектра входного сигнала кратными частоте передачи данных. Кроме того, спектр сигнальной линии содержит только положительные частоты и не содержит частот в области нуля. Спектр входного сигнала содержит положительные, нулевую и отрицательные частоты.
Для преобразования характеристики сигнальной линии в передаточную функцию – характеристику, частоты которой совпадают с частотами спектра входного сигнала, выполнены следующие шаги.
1. Вычисление амплитуды характеристики линии на нулевой частоте путем ее экстраполяции. Для этого по десяти точкам амплитудной характеристики, ближайших к нулевой частоте, найдены коэффициенты линейного полинома, аппроксимирующего амплитудную характеристику:
Найденный второй коэффициент полинома равен амплитуде характеристики на нулевой частоте:
2. Фазовая характеристика на нулевой частоте принята равной нулю.
3. Пересчет амплитудной channel.abs и фазовой channel.phase характеристик сигнальной линии со значениями на нулевой частоте выполняется на частоты спектра входного сигнала (f = -fmax/2:fmax/points:fmax/2-fmax/points) с экстраполяцией характеристик в область нулевой и отрицательных частот:
Полученная передаточная функция — амплитудно-фазовая частотная характеристика канала в области низких частот показана на Рисунок 7. Амплитудно-частотные характеристики измеренной сигнальной линии и расчетной передаточной функции в полных частотных диапазонах показаны на Рисунок 8. Эти же характеристики в фазовом пространстве показаны на Рисунок 9.
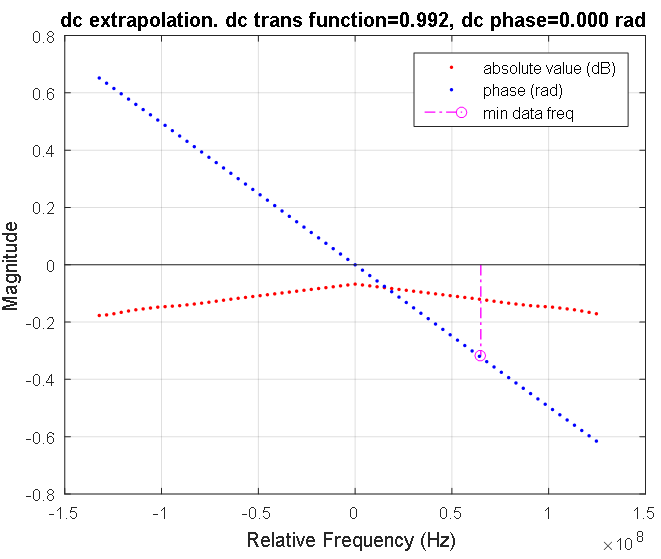
Рисунок 7. Передаточная функция сигнальной линии в области низких частот. Красными и синими точками обозначены дискретные амплитудная и фазовая характеристики соответственно. Амплитудная характеристика показана в децибелах, фазовая — в радианах. Розовой линией отмечена самая низкая частота измеренной характеристики сигнальной линии. Коэффициент передачи на нулевой частоте равен 0,992.
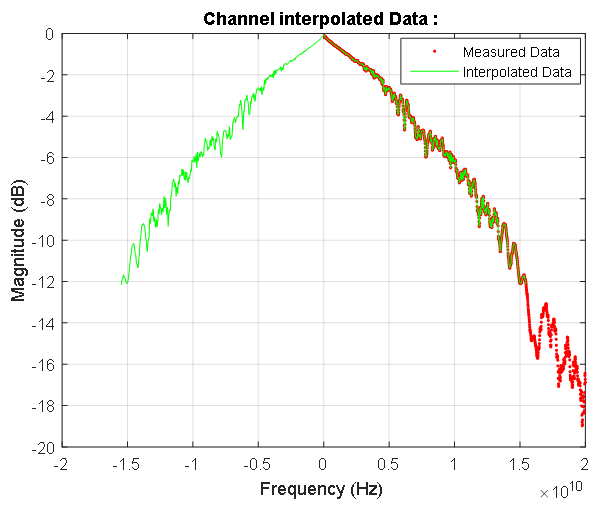
Рисунок 8. Амплитудно-частотные характеристики сигнальной линии. Синими точками обозначены комплексные данные измеренной линии. Расчетная симметричная зависимость усиления сигнальной линии на частотах спектра входного сигнала выделена красным. В области нулевых частот эта характеристика показана на Рисунок 7.

Рисунок 9. Амплитудно-фазовые частотные характеристики измеренной линии передачи данных и ее нормированного спектра.
Реакция (отклик на входное воздействие) в частотной области получается перемножением спектра сигнала на произведение передаточных функций элементов, которые связывают реакцию с входным сигналом. В нашем случае сигнал проходит через фильтр и сигнальную линию.
Для перевода сигнала из частотной области во временную область используется обратное преобразование Фурье ifft.
Выходной сигнал фильтра во временной области iSignal.Filter_out вычисляется как
Выходной сигнал линии iSignal.Rx равен произведению спектра входного сигнала на передаточные функции фильтра и сигнальной линии с последующим переводом полученного сигнала из частотной области во временную область.
Реакция фильтра на входной идеальный импульс и реакция канала показаны на Рисунок 10.
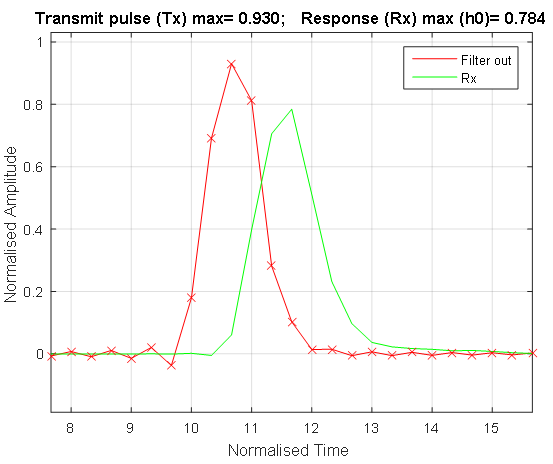
Рисунок 10. Выходной сигнал фильтра (красный график) и выходной сигнал линии передачи данных (зеленый график). Входной сигнал фильтра – единичный импульс показан на Рисунок 2. Входом сигнальной линии является выходной сигнал фильтра.
1. IEEE802.3ap. 10.3125Gbps NRZ Simulation Results Using “StatEye” and “Signal to Interference Model” on Cascaded Channel Components. Shannon Sawyer and Charles Moore / Agilent Technologies. January 24, 2005 www.ieee802.org/3/ap/public/jan05/sawyer_01_0105.pdf
2. What is StatEye. IEEE 803.3ap Task Force. September 16, 2004 www.ieee802.org/3/ap/public/signal_adhoc/ghiasi_01_0904.pdf
3. Stat Eye / IBM Agreement. Steve Anderson. Xilinx, Inc. www.ieee802.org/3/ap/public/nov04/anderson_01_1104.pdf
Условие задачи
Необходимо определить изменение формы двоичного цифрового сигнала проходящего через фильтр и сигнальную линию. Сигнал задан амплитудой и скоростью передачи. Фильтр второго порядка, нормированный относительно частоты передачи данных, задан постоянными времени. Передаточная функция сигнальной линии представлена измеренной частотной характеристикой в комплексной форме.
Среда, используемая для вычисления и отображения данных – MATLAB R2015а.
В качестве примера исходных данных взяты следующие отношения, опубликованные на сайте www.StatEye.org для версии метода StatEye 3.0 GUI [1, 2, 3].
Скорость передачи данных bps = 10,3125 Гбит/с. Постоянные времени нормированного фильтра второго порядка совпадают, их обратная величина составляет ¾ частоты передачи данных. Сигнальная линия представлена частотной характеристикой. Измерение характеристики выполнено на частотах channel.f = 0,006495:0,0012475:20 ГГц. Заданное число точек дискретизации преобразования Фурье: points = 2^13.
На Рисунок 1 показаны передача данных, последовательность и результаты обработки данных, которые рассмотрены в этой работе. Переход из временной области в частотную область и обратно выполняется при помощи алгоритма Быстрого Преобразования Фурье (БПФ, FFT).

Рисунок 1. Канал передачи данных. Входной сигнал iSignal.Tx, выходной сигнал фильтра iSignal.Filter_out, выход сигнальной линии iSignal.Rx. Представленные на диаграмме характеристики рассмотрены ниже.
Последовательность вычислений
В этой работе основные вычисления выполнены в частотной области. Для этого, исходный сигнал из временной области переведен в частотную область с использованием преобразования Фурье, перемножением спектральных характеристик сигнала, фильтра и сигнальной линии найден выходной сигнал тракта, который из частотной области переведен во временную область обратным преобразованием Фурье.
Скорость передачи данных в два раза выше частоты, на которой происходит передача данных. Максимальная частота измеренной сигнальной линии max(channel.f) = 20 ГГц. На этой частоте можно передавать данные со скоростью 40 Гбит/с (как 2*max(channel.f)).
Максимальная скорость передачи данных, которая не превышает максимальную скорость передачи по сигнальной линии 40 Гбит/с и кратная скорости передачи bps = 10,3125 Гбит/с, равна fmax = 30,9375 Гбит/с, кратность N = 3 (N = fmax/bps). Далее, fmax используется как предельная частота для расчета реакции сигнала с применением преобразования Фурье.
Перевод входного сигнала в частотную область
Дискретность по времени для построения входного сигнала (бита данных) во временной области Ts = 1/fmax; Ts = 3,232e-11 с. Нормированная по отношению к длительности сигнала, временная шкала time состоит из 2^13 точек (points), шкала включает следующий массив точек time = bps/Ts .* (1:points). Дискретный единичный сигнал при скорости передачи bps = 10,3125 Гбит/с и квантовании с периодом Ts = 1/fmax состоит из трех точек в диапазоне от 10 до 11 единиц нормализованного времени. Сигнал единичной амплитуды можно построить и в любом другом месте временной шкалы, но лучше отступить с краев, чтобы полностью видеть предысторию и переходный процесс выходного сигнала. Импульсный сигнал (бит данных), построенный с использованием следующих команд МАТЛАБ, показан на Рисунок 2.
iSignal.Tx(1:size(time,2)) = 0;
t0 = max(find(time<=10));
t1 = max(find(time<11));
iSignal.Tx(t0:t1) = 1.0;
Рисунок 2. Входной импульсный сигнал iSignal.Tx, бит данных.
Перевод сигнала iSignal.Tx в частотную область выполняют следующие БПФ функции.
iSignal.shiftedPSD = fft(iSignal.Tx);
iSignal.PSD = fftshift(iSignal.shiftedPSD);Функция преобразования Фурье fft строит симметричный спектр сигнала в областях положительных и отрицательных частот, максимальная частота которого находится в центре спектра (см. Рисунок 3). Функция fftshift восстана��ливает спектр, сдвигая в центр нулевую частоту сигнала как показано на Рисунок 4.
Разрешение частоты спектра равно fs = fmax/points; Частоты спектра лежат в диапазоне от -fmax/2 до fmax/2-fs и равны f = -fmax/2:fs:fmax/2-fs;

Рисунок 3. Амплитудная характеристика сдвинутого спектра сигнала iSignal.Tx полученного с использованием БПФ.

Рисунок 4. Амплитудная характеристика восстановленного спектра сигнала iSignal.Tx показанного на Рисунок 3. Представлено 2^13 отсчетов. Средний отсчет в точке 4097 соответствует нулевой частоте. В левой части (от 1 до 4096 точки) располагаются отрицательные частоты, в правой части (от 4098 до 8192 точки) – область положительных частот.
Передаточная функция нормализованного фильтра нижних частот
В этом примере передаточная функция фильтра второго порядка имеет вид
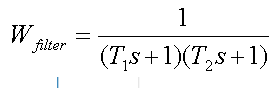
где Т1 и Т2 – постоянные времени фильтра. Значения частот 1/T1 равны и 1/T2 заданы относительно частоты, на которой передаются данные: 1/T1 = 1/T2 = 0,75*bps (bps = 10,3125 Гбит/с).
Полоса частот нормализованного фильтра
f_nrm =fmax/bps/points.*(-points/2:points/2-1).Оператор
s = f_nrm .* j;Амплитудно-фазовая характеристика нормализованного фильтра для положительных и отрицательных частот нормализованных относительно частоты передачи сигнала показана на Рисунок 5. Логарифмическая амплитудно-частотная характеристика фильтра показана на Рисунок 6.

Рисунок 5. Амплитудно-фазовая характеристика нормализованного фильтра

Рисунок 6. Логарифмическая амплитудно-фазовая частотная характеристика нормализованного фильтра. Синяя штриховая линия показывает положение частоты фильтра со значением 0,75 от частоты, на которой идет передача данных. На этой частоте (1/T1 = 1/T2) коэффициент передачи фильтра второго порядка равен -6 децибел. Красная штриховая линия показывает единичную частоту, на которой идет передача данных.
Перевод результатов измерения сигнальной линии к виду передаточной функции
Измеренная амплитудно-фазовая характеристика сигнальной линии включает 1599 отсчетов в полосе до 20 ГГц с фиксированным шагом 12,475 МГц. Она содержит следующие значения частот: channel.f = 0,006495:0,0012475:20 ГГц. Изначально, сигнальная линия была представлена характеристикой четырехполюсника. Эта характеристика была преобразована и в примере используется в виде одномерной комплексной функции.
Частоты характеристики сигнальной линии, полученные в результате измерения, не совпадают с частотами спектра входного сигнала кратными частоте передачи данных. Кроме того, спектр сигнальной линии содержит только положительные частоты и не содержит частот в области нуля. Спектр входного сигнала содержит положительные, нулевую и отрицательные частоты.
Для преобразования характеристики сигнальной линии в передаточную функцию – характеристику, частоты которой совпадают с частотами спектра входного сигнала, выполнены следующие шаги.
1. Вычисление амплитуды характеристики линии на нулевой частоте путем ее экстраполяции. Для этого по десяти точкам амплитудной характеристики, ближайших к нулевой частоте, найдены коэффициенты линейного полинома, аппроксимирующего амплитудную характеристику:
[a] = polyfit(channel.f(1:10), channel.abs(1:10), 1);Найденный второй коэффициент полинома равен амплитуде характеристики на нулевой частоте:
channel.dc = a(2);2. Фазовая характеристика на нулевой частоте принята равной нулю.
channel.dcPhase = 0.00;3. Пересчет амплитудной channel.abs и фазовой channel.phase характеристик сигнальной линии со значениями на нулевой частоте выполняется на частоты спектра входного сигнала (f = -fmax/2:fmax/points:fmax/2-fmax/points) с экстраполяцией характеристик в область нулевой и отрицательных частот:
ichannel.abs = interp1([0 channel.f], [channel.dc channel.abs], abs(f), 'linear', 'extrap');
ichannel.phase = interp1([0 channel.f], [channel.dcPhase unwrap(channel.phase)], abs(f), 'linear', 'extrap');
ichannel.s = ichannel.abs .* exp(+j.*ichannel.phase);
ichannel.tf = real(ichannel.s) + j*imag(ichannel.s) .* sign(f);Полученная передаточная функция — амплитудно-фазовая частотная характеристика канала в области низких частот показана на Рисунок 7. Амплитудно-частотные характеристики измеренной сигнальной линии и расчетной передаточной функции в полных частотных диапазонах показаны на Рисунок 8. Эти же характеристики в фазовом пространстве показаны на Рисунок 9.

Рисунок 7. Передаточная функция сигнальной линии в области низких частот. Красными и синими точками обозначены дискретные амплитудная и фазовая характеристики соответственно. Амплитудная характеристика показана в децибелах, фазовая — в радианах. Розовой линией отмечена самая низкая частота измеренной характеристики сигнальной линии. Коэффициент передачи на нулевой частоте равен 0,992.

Рисунок 8. Амплитудно-частотные характеристики сигнальной линии. Синими точками обозначены комплексные данные измеренной линии. Расчетная симметричная зависимость усиления сигнальной линии на частотах спектра входного сигнала выделена красным. В области нулевых частот эта характеристика показана на Рисунок 7.

Рисунок 9. Амплитудно-фазовые частотные характеристики измеренной линии передачи данных и ее нормированного спектра.
Вычисление реакции сигнала
Реакция (отклик на входное воздействие) в частотной области получается перемножением спектра сигнала на произведение передаточных функций элементов, которые связывают реакцию с входным сигналом. В нашем случае сигнал проходит через фильтр и сигнальную линию.
Для перевода сигнала из частотной области во временную область используется обратное преобразование Фурье ifft.
Выходной сигнал фильтра во временной области iSignal.Filter_out вычисляется как
TransFunction.PSD = iSignal.PSD .* Filter.PSD_Tx;
TransFunction.shiftedPSD = ifftshift(TransFunction.PSD);
iSignal.Filter_out = real(ifft(TransFunction.shiftedPSD));Выходной сигнал линии iSignal.Rx равен произведению спектра входного сигнала на передаточные функции фильтра и сигнальной линии с последующим переводом полученного сигнала из частотной области во временную область.
TransFunction.PSD = TransFunction.PSD .* ichannel.tf;
TransFunction.shiftedPSD = ifftshift(TransFunction.PSD);
iSignal.Rx = real(ifft(TransFunction.shiftedPSD)); Реакция фильтра на входной идеальный импульс и реакция канала показаны на Рисунок 10.

Рисунок 10. Выходной сигнал фильтра (красный график) и выходной сигнал линии передачи данных (зеленый график). Входной сигнал фильтра – единичный импульс показан на Рисунок 2. Входом сигнальной линии является выходной сигнал фильтра.
Приложение. Используемый m-код MATLAB
Листинг
clear all
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Ini data
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
bps = 1.03125e+10;
FilterParam = [0.75 0.75];
points = 2^13;
load('channel');
N = floor(max(channel.f)*2/bps);
fmax = N*bps;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Signal
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% normalise all the scales for the bit rate
time = bps/fmax .* (1:points);
iSignal.Tx(1:size(time,2)) = 0;
t0 = max(find(time<=10));
t1 = max(find(time<11));
iSignal.Tx(t0:t1) = 1.0;
figure
plot(time(1:t1+10), iSignal.Tx(1:t1+10),'b');
hold on
plot(time(1:t1+10), iSignal.Tx(1:t1+10),'xb');
grid on
xlabel('Normalised Time, tick Ts = 1/fmax');
ylabel('Normalised Amplitude');
title(['Pulse, data bit']);
iSignal.shiftedPSD = fft(iSignal.Tx);
figure
plot(abs(iSignal.shiftedPSD),'c');
grid on
xlabel('points, num');
ylabel('Amplitude');
title(['abs(fft(iSignal.Tx))']);
iSignal.PSD = fftshift(iSignal.shiftedPSD);
figure
plot(abs(iSignal.PSD),'r');
grid on
xlabel('points, num');
ylabel('Amplitude');
title(['abs(fftshift(fft(iSignal.Tx)))']);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Filter
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
f_nrm =fmax/bps/points.*(-points/2:points/2-1);
s = f_nrm .* j;
Filter_PSD = 1 ./(1 + s/FilterParam(1)) ./ (1 + s/FilterParam(2));
figure
[AX,H1,H2] = plotyy (f_nrm, abs(Filter_PSD), f_nrm, phase(Filter_PSD));
hold(AX(1));
hold(AX(2));
set(H1,'LineWidth',2);
grid(AX(2),'on');
xlabel('Normalised Frequency (Hz)');
set(get(AX(1),'Ylabel'),'String','Gain');
set(get(AX(2),'Ylabel'),'String','Phase, rad');
title(['Twopole filter [' sprintf(' %3.2f ', FilterParam) '] normalised to baud rate frequency']);
figure
plot_handles_Filter = plot(f_nrm(points/2 + 1:points), 20*log10(abs(Filter_PSD(points/2 + 1:points))), 'r', 'linewidth', 2);
hold on
stem_handles_br = stem(1, 20*log10(abs(Filter_PSD(max(find(f_nrm < 1))))), '-.ro');
hold on
stem_handles_c = stem(FilterParam, [20*log10(abs(Filter_PSD(max(find(f_nrm < FilterParam(1)))))) 20*log10(abs(Filter_PSD(max(find(f_nrm < FilterParam(2))))))], '-.bo');
grid
legend_handles = [plot_handles_Filter, stem_handles_br(1), stem_handles_c(1)];
legend(legend_handles, 'transfer function', 'filter attenuation at normalised baud rate', 'filter attenuation at normalised cutoff frequency', 3);
xlabel('Normalised Frequency (Hz)');
ylabel('Magnitude (dB)');
title(['Twopole filter [' sprintf(' %3.2f ', FilterParam) '] normalised to baud rate frequency']);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Channel
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% create negative frequencies, convert data to complex value, taking care about negative frequency
channel.abs = abs(channel.s);
channel.phase = angle(channel.s);
%channel.s = channel.abs .* exp(+j.*channel.phase);
[a] = polyfit(channel.f(1:10), channel.abs(1:10), 1);
channel.dc = a(2);
channel.dcPhase = 0.00;
fs = fmax/points; % frequency step
f = -fmax/2:fs:fmax/2-fs; % frequency matrix
% create new data structure with linearly interpolated data
ichannel.abs = interp1([0 channel.f], [channel.dc channel.abs], abs(f), 'linear', 'extrap');
ichannel.phase = interp1([0 channel.f], [channel.dcPhase unwrap(channel.phase)], abs(f), 'linear', 'extrap');
% correct for negative frequencies
ichannel.s = ichannel.abs .* exp(+j.*ichannel.phase);
ichannel.tf = real(ichannel.s) + j*imag(ichannel.s) .* sign(f);
figure
disp_points = 2*round(channel.f(1)/fs);
stem_handles_br = stem(channel.f(1), angle(ichannel.tf(max(find(f < channel.f(1))))), '-.mo');
hold on
plot_abs = plot(f(points/2-disp_points:points/2+disp_points), 20*log10(abs(ichannel.tf(points/2-disp_points:points/2+disp_points))), '.r', 'linewidth', 3);
hold on
plot_phase = plot(f(points/2-disp_points:points/2+disp_points), angle(ichannel.tf(points/2-disp_points:points/2+disp_points)), '.b', 'linewidth', 3);
grid
legend_handles = [plot_abs, plot_phase, stem_handles_br(1)];
legend(legend_handles, 'absolute value (dB)', 'phase (rad)', 'min data freq', 3);
xlabel('Relative Frequency (Hz)');
ylabel('Magnitude');
title(sprintf('dc extrapolation. dc trans function=%4.3f, dc phase=%4.3f rad', abs(ichannel.tf(points/2+1)), angle(ichannel.tf(points/2+1))));
figure
plot(channel.f, 20*log10(channel.abs), '.r', 'linewidth', 3);
hold on
plot(f, 20*log10(ichannel.abs), 'g');
grid on
legend('Measured Data', 'Interpolated Data', 3);
xlabel('Frequency (Hz)');
ylabel('Magnitude (dB)');
title(['Chаnnel interpolated Data : ']);
figure
plot3(channel.f, real(channel.s), imag(channel.s),'r');
hold on
plot3(f, real(ichannel.tf), imag(ichannel.tf),'g');
grid on
legend('Measured Data', 'Interpolated Data');
xlabel('Frequency in Hz');
ylabel('Re(fwd transfer)');
zlabel('Im(fwd transfer)');
title(['Chаnnel interpolated Data : ']);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Response
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% filter Output
TransFunction.PSD = iSignal.PSD .* Filter_PSD;
TransFunction.shiftedPSD = ifftshift(TransFunction.PSD);
iSignal.Filter_out = real(ifft(TransFunction.shiftedPSD));
% pass through channel
TransFunction.PSD = TransFunction.PSD .* ichannel.tf;
TransFunction.shiftedPSD = ifftshift(TransFunction.PSD);
iSignal.Rx = real(ifft(TransFunction.shiftedPSD));
figure
plot(time, iSignal.Filter_out,'r');
hold on
[max_Tx, time_maxTx] = max(iSignal.Filter_out);
[min_Tx, time_minTx] = min(iSignal.Filter_out);
[max_Rx, time_maxRx] = max(iSignal.Rx);
dtime_p5= round((time_maxRx - time_maxTx)*time(1) -1);
plot(time - dtime_p5, iSignal.Rx,'g');
hold on
plot(time, iSignal.Filter_out,'rx');
axis([(time_maxTx*time(1) - 3) (time_maxTx*time(1) + 5) (min_Tx-0.15) (max_Tx+0.1)])
grid on
legend('Filter out','Rx', 2);
xlabel('Normalised Time');
ylabel('Normalised Amplitude');
title(sprintf('Transmit pulse (Tx) max= %4.3f; Response (Rx) max (h0)= %4.3f', max(iSignal.Filter_out), max(iSignal.Rx)));
Библиографический список
1. IEEE802.3ap. 10.3125Gbps NRZ Simulation Results Using “StatEye” and “Signal to Interference Model” on Cascaded Channel Components. Shannon Sawyer and Charles Moore / Agilent Technologies. January 24, 2005 www.ieee802.org/3/ap/public/jan05/sawyer_01_0105.pdf
2. What is StatEye. IEEE 803.3ap Task Force. September 16, 2004 www.ieee802.org/3/ap/public/signal_adhoc/ghiasi_01_0904.pdf
3. Stat Eye / IBM Agreement. Steve Anderson. Xilinx, Inc. www.ieee802.org/3/ap/public/nov04/anderson_01_1104.pdf
