Доброго времени суток, Хабр
Настоящей статьей открываю цикл статей о том, как обучать нейронные сети без учителя.
(Reinforcement Learning for Neuron Networks)
В цикле планирую сделать три статьи по теории и реализации в коде трех алгоритмов обучения нейронных сетей без учителя. Первая статья будет по Policy Gradient, вторая по Q-learning, третья статья заключительная будет по методу Actor-Critic.
Приятного чтения.
Статья Первая — Обучение без учителя методом Policy Gradient
(Policy Gradient for Reinforcement Learning)
Введение
Среди алгоритмов машинного обучения особое место занимают алгоритмы машинного обучения где алгоритм учится решать поставленную задачу самостоятельно без участия человека, напрямую взаимодействуя со средой в которой он обучается.
Такие алгоритмы получили общее название — алгоритмы обучения без учителя, для таких алгоритмов не нужно собирать базы данных, не нужно производить их классификацию или разметку.
Алгоритму обучающемуся без учителя достаточно только давать обратный отклик на его действия или решения — хороши они были или нет.
Глава 1. Обучение с учителем
Так что же это такое — Обучение с учителем или без. Разберемся более подробно в этом на примерах из современного машинного обучения и задач которые оно решает.
Большинство современных алгоритмов машинного обучения для задач классификации, регрессии, сегментации являются по сути алгоритмами обучения с учителем в которых учителем выступает сам человек. Потому что именно человек размечая данные говорит алгоритму какой должен быть правильный ответ и тем самым алгоритм пытается найти такое решение, чтобы ответ который выдает алгоритм при решении задачи максимально совпадал с ответом который указал человек для данной задачи как правильный ответ.
На примере задачи классификации для датасета Mnist правильным ответом который дает человек алгоритму — это будет метка класса цифры в обучающей выборке.

В дата сете Mnist для каждого изображения которое машинному алгоритму предстоит научиться классифицировать люди заранее проставили правильные метки к какому классу относится это изображение. В процессе обучения алгоритм предсказывая класс изображения сравнивает свой полученный класс для конкретного изображения с истинным классом для этого же изображения и постепенно в процессе обучения так корректирует свои параметры, чтобы предсказанный алгоритмом класс стремился соответствовать заданному человеком классу.
Таким образом можно обобщить следующую мысль — алгоритмом обучения с учителем является любой алгоритм машинного обучения, где мы выдаем алгоритму как ему нужно с нашей точки зрения правильно поступить.
И это не важно как именно поступить — указать к какому классу отнести данное изображение если это задача классификации, или отрисовать контуры предмета если это задача сегментации или в какую сторону повернуть рулевое колесо автомобиля если алгоритм это автопилот, важно то, что для каждой конкретной ситуации мы явно указываем алгоритму где правильный ответ, как правильно ему поступить.
Это и есть ключ к пониманию того, чем принципиально алгоритм обучения с учителем отличается от алгоритма обучения без учителя.
Глава 2. Обучение без учителя
Разобравшись что же это такое — обучение с учителем, разберемся теперь, что же это такое — обучение без учителя.
Как мы выяснили в прошлой главе, при обучении с учителем мы для каждой обучающей ситуации, даем алгоритму понимание, какой ответ с нашей точки зрения тут правильный, то идя от противного — в обучении без учителя, для каждой конкретной ситуации мы такого ответа алгоритму давать не будем.
Но тогда возникает вопрос, если мы не даем алгоритму явного указания как поступ��ть правильно, то чему же алгоритм научится? Как алгоритм будет обучаться не зная куда ему корректировать свои внутренние параметры, чтобы поступать правильно и в конечном итоге решить задачу так как нам бы хотелось.
Давайте подумаем, на эту тему. Нам же важно, чтобы алгоритм решил задачу в целом, а как конкретно он будет поступать в процессе решения этой задачи и каким путем он пойдет, чтобы ее решить это нас не касается, отдадим это решать самому алгоритму, мы же от него ожидаем только конечный результат.
Поэтому конечному результату мы и дадим алгоритму понять, хорошо он решил нашу задачу или нет.
Таким образом так же обобщая все вышесказанное, мы приходим к выводу, что алгоритмом обучения без учителя мы называем такие алгоритмы, где нет явных указания для алгоритма как ему поступать, а есть только общая оценка всех его действий в процессе решения задачи.
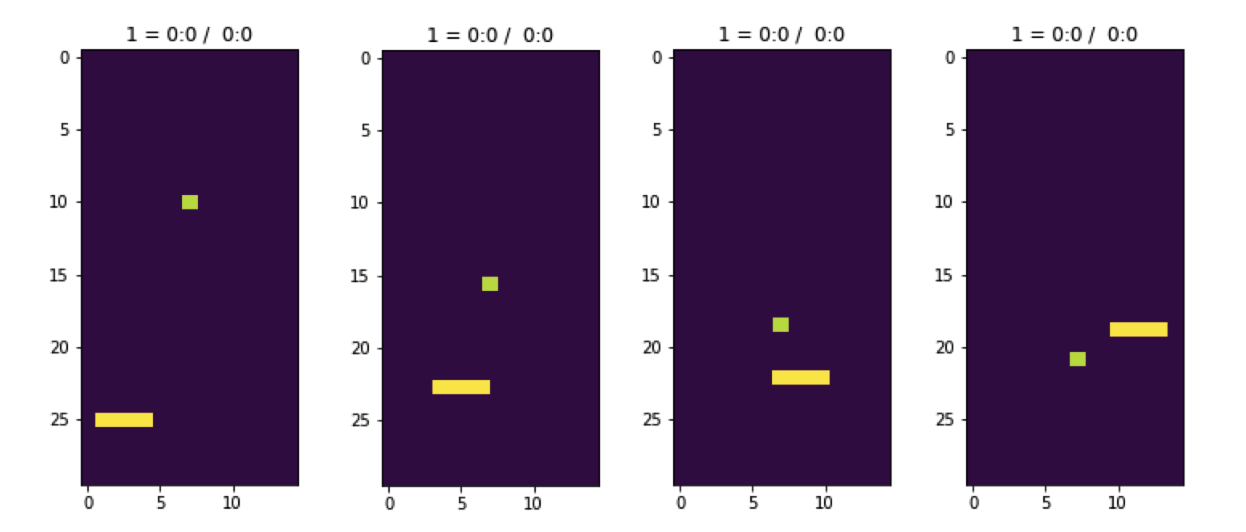
На примере игры где ракетка пытается поймать кубики падающие сверху мы не говорим алгоритму управляющему ракеткой в какой конкретно момент времени куда двигать ракетку. Мы скажем алгоритму только результат его действий — поймал он ракеткой кубик или нет.



Это и есть суть обучения без учителя. Алгоритм сам должен научиться решать как ему поступать в каждом конкретном случае исходя из конечной оценки совокупности всех его действий.
Глава 3. Агент, Среда и Награда
Разобравшись с тем, что такое обучение без учителя, углубимся в алгоритмы которые умеют обучаться решению какой либо задачи без наших подсказок как правильно им поступать.
Настало время ввести нам терминологию которой мы будем пользоваться в дальнейшем.
Агентом мы будем называть наш алгоритм который умеет анализировать состояние среды и совершать в ней какие-то действия.
Среда — виртуальный мир в котором существует наш Агент и своими действиями может менять его состояние…
Награда — обратная связь от Среды к Агенту как ответ на его действия.
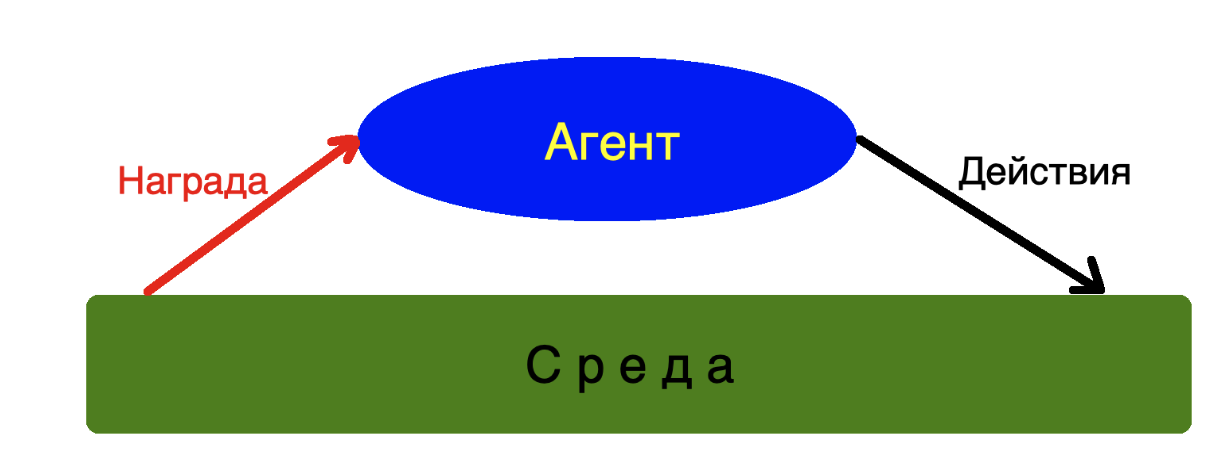
Среда в которой обитает наш агент может быть сколь угодно сложной, агент может и не знать вовсе как она устроена, чтобы принимать свои решения и выполнять действия. Для Агента важна лишь обратная связь в виде награды которую он получает от среды.
Если более подробно рассмотреть процесс взаимодействия агента со средой то его можно выразить следующей схемой
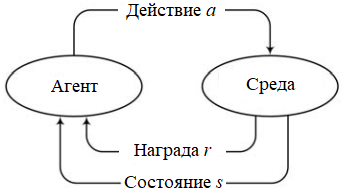
St — состояние среды (state) на шаге t
at — действие агента (action) на шаге t
rt — награда (reward) на шаге t
В каждый момент времени t наш агент наблюдает состояние среды — St, выполняет действие — at, за что получает от среды награду — rt, поле чего среда переходит в состояние St+1, которое наблюдает наш агент, выполняет действие — at+1, за что получает от среды награду — rt+1 и таких состояний t у нас может быть бесконечное множество — n.
Глава 4. Параметризация задачи обучения без учителя
Для того чтобы обучать агента нам нужно его как-то параметризовать задачу обучения без учителя, другими словами понять что за функции мы собираемся оптимизировать. В reinforcement learning — в дальнейшем мы так будем называть обучение без учителя, существует три таких основных функции:
1) p(a|s) — policy function
Функция вероятности оптимальности действия — a в зависимости от состояния среды -s. Она показывает нам насколько действие a при состоянии среды s оптимально.
2) v(s) — value function
Функция ценности состояния — s. Она показывает нам насколько состояние s вообще ценно для нас с точки зрения награды
3) Q(s,a) — Q-function
Q функция оптимальной стратегии. Она позволяет нам согласно данной оптимальной стратегии в состоянии — s выбрать оптимальное для этого состояния действие — a
Первой рассмотрим функцию — policy function, как наиболее простую и интуитивно понятную для понимания функцию reinforcement learning.
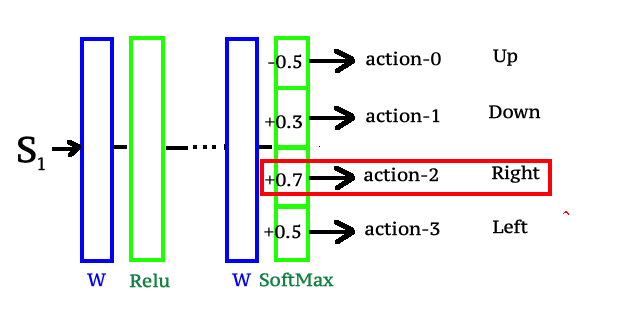
Поскольку мы собираемся решать задачи reinforcement learning посредством нейронных сетей. То схематично мы можем параметризовать policy function через нейронную сеть следующим образом.
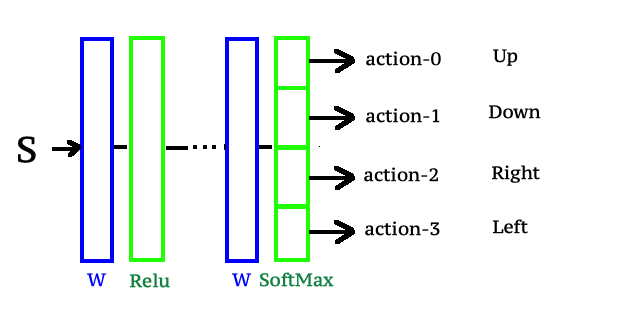
На вход нейронной сети, будем подавать состояния — s, а выход нейросети сконструируем таким образом, чтобы выходным слоем нейросети был слой SoftMax, с количеством выходов равным количеству действий возможных для агента в нашей среде. Таким образом пропустив через слои нейросети состояние s на выходе мы получим распределение вероятностей для действий агента в состоянии s. Что собственно нам и требуется для того чтобы начать через алгоритм обратного распространения ошибки обучать нашу нейросеть и итеративно улучшать policy function, которая теперь по сути является нашей нейронной сетью.
Глава 5. Улучшение policy function через обучение нейросети
Для обучения нейросети мы используем метод градиентного спуска. Поскольку последний слой нашей нейросети это SoftMax слой, его Loss функция равна:
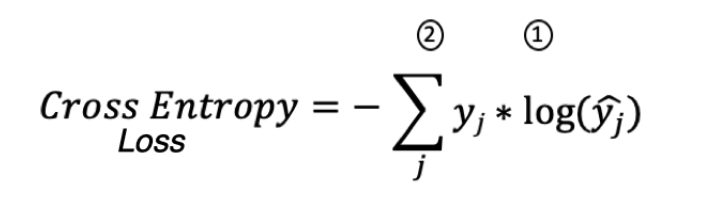
где:
1 — истинные метки * log(предсказанные метки)
2 — сумма по всем примерам
Однако как же нам обучать нейросеть если у нас пока нет правильных меток для действий агента в состояниях S0-Sj? А они нам и не нужны, мы вместо правильных меток будем использовать награду которую агент получил от среды выполнив действие которое ему предсказала нейросеть.
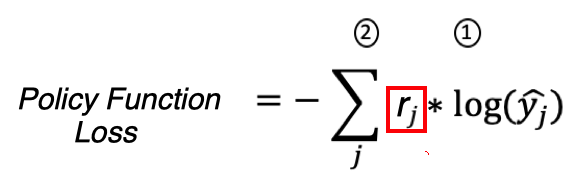
Имеем полное право так сделать потому что, для Cross Entropy Loss — yj — это истинные метки и для правильного класса и они равны единице, а для Policy Function Loss — rj — награда которую среда начислила агенту за действие которое он совершил. То есть rj служит как бы весом для градиентов при обратном распространении ошибки когда мы обучаем нейросеть.
Получена положительная награда — значит нужно увеличить веса нейросети куда градиент направлен.
Если полученная награда отрицательная, значит соответствующие веса в нейросети, согласно направления градиента куда направлена ошибка уменьшаем.
Глава 6. Сборка ДатаСета для обучения
Для того чтобы обучать нашего Агента — нейросеть средствами классического Machine Learning — через метод обратного распространения ошибки, нам нужно собрать датасет.
Из постановки задачи понятно, что на вход нейросети мы хотим подавать состояние среды S — изображение колодца с падающими кубиками и ракеткой которая их ловит.

а Y — который мы соберем в соответствии с состоянием S, это будет предсказанное действие нейросети — а и награда которую среда начислила агенту за это действие — r
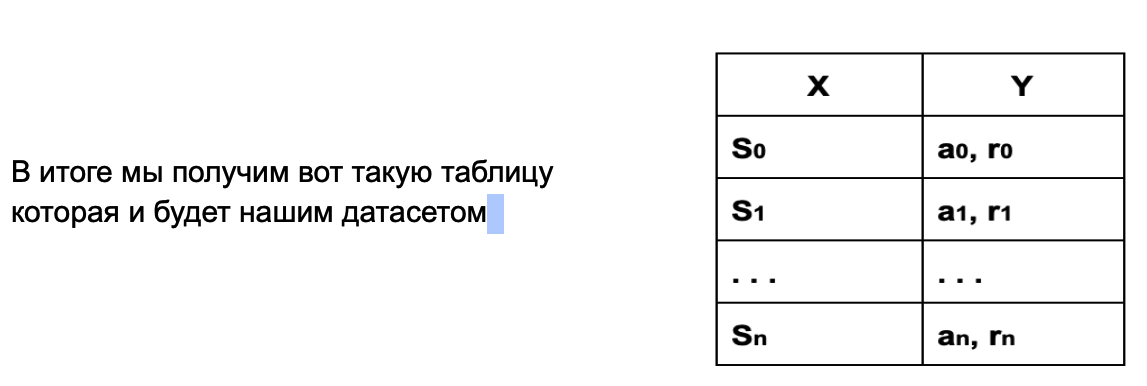
Но ведь среда по ходу игры может не за каждое действие агенту начислять награду, например в нашем случае агент получит положительную награду только тогда, когда ракетка поймает падающий кубик. В случае если ракетка кубик не поймает и он упадет на дно, то среда начислит агенту отрицательную награду. Все остальное время вне зависимости от того как агент двигает ракетку, пока кубик либо не ударится о ракетку, либо не упадет на дно, среда будет начислять агенту награду равную нулю.

Как видно из описания процесса нашей игры, положительная или отрицательная награда у агента случается крайне редко, в основном же награда вне зависимости от его действий равна нулю. Как же обучать Агента кода основное время он не получает отклика от среды на свои действия. С точки зрения того, что наш агент — нейросеть и награда от среды равна нулю, то и градиенты при обратном распространении ошибки через нейросеть в большинстве случаев в датасете будут равны нулю, весам нейросети меняться будет некуда, значит и наш агент ничему не будет учиться.
Как же решить проблему с нулевой наградой в большей части датасета который собирается для обучения агента?
Выйти из данной ситуации можно двумя способами:
первый — присвоить всем действиям агента которые он предпринимал за время пока кубик падал одну и туже финальную награду эпизода +1 или -1, в зависимости от того поймал агент кубик или не поймал.
Тем самым мы все действия Агента если он поймал кубик будем считать правильными и будем закреплять такое поведение агента при обучении, присвоив им положительную награду. В случае если Агент кубик не поймал, то всем действиям Агента в эпизоде мы присвоим отрицательную наград�� и будем обучать его избегать такой последовательности действий в дальнейшем.
второй — финальную награду с определенным шагом дисконта по убыванию распространить на все действия агента в этом эпизоде. Иначе говоря, чем ближе к финалу действие агента тем ближе к +1 или -1 награда за это действие.
Введя такую дисконтированную награду за действие с убыванием по мере удаления действия от финала эпизода, мы даем Агенту понять, что последние действия которые он предпринимал, более важны для результат эпизода Игры, чем те действия которые он предпринимал вначале.
Обычно дисконтированная награда рассчитывается по формуле — Финальная награда эпизода умножается на коэффициента дисконта в степени номера шага минус один для всех действиях агента в эпизоде (за то время, что падал кубик).
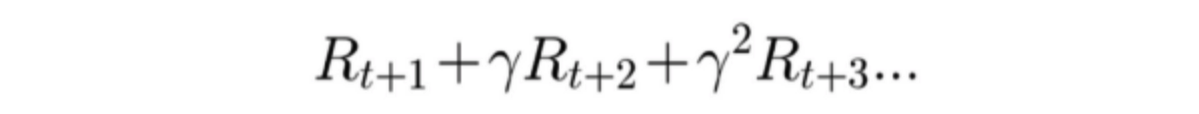
Гамма — коэффициент дисконтирования (убывания награды). Он всегда находится в диапазоне от 0 до 1. Обычно гамму берут в районе 0.95
После того как определились с тем какие данные мы собираем в ДатаСет, запускаем симулятор среды и проигрывая подряд несколько раз игру с несколькими эпизодами, собираем данные о:
- состоянии Среды,
- действиях которые предпринял Агент,
- награду которую Агент получил.
Для простоты понимания назовем падение одного кубика через колодец — эпизодом игры, примем также, что сама игра будет состоять из нескольких эпизодов. Это значит, что за одну игру мы будем сбрасывать в колодец несколько кубиков по очереди, а ракетка будет пытаться их поймать. За каждый пойманный кубик агенту будет начисляться +1 балл, за каждый кубик что упал на дно и ракетка его не поймала, агенту будет начисляться -1 балл.
Глава 7. Внутреннее устройство агента и среды
Среда — поскольку у нас среда в которой предстоит существовать агенту по сути представляет из себя матрицу колодца внутри которой со скоростью одна строка за такт падают вниз кубики, а агент ходит в одном из направлений тоже на одну клетку.
Мы напишем симулятор среды, который умеет в случайный момент времени сбрасывать с верхней строчки по произвольному столбцу кубик, умеет получив команду от агента перемещать ракетку на одну клетку в одном из направлений, после чего проверяет был ли падающий кубик пойман ракеткой или может быть он упал на дно колодца. В зависимости от этого симулятор возвращает агенту награду которую он получил за свое действие.
Агент — основной элемент которого это наша нейросеть способная по состоянию среды преданной ей на вход возвращать вероятности всех действий для данного состояния среды. Из полученных от нейросети вероятности действий, агент выбирает лучшее, отправляет его в среду, получает от среды обратную связь в виде награды от среды. Также Агент должен обладать внутренним алгоритмом на основе которого он будет способен обучаться максимизировать награду получаемую от среды.
Глава 8. Обучение Агента
Для того чтобы обучать Агента нам нужно накопить статистику по данным от нашего симулятора и действий предпринятым агентом. Статистический данные для обучения мы будем собирать тройками значений — состояние среды, действие агента и награда за это действие.

Немного кода как собираем статистику

Каждую такую тройку значений мы помещаем в специальный буфер памяти, где храним их все время пока проводим симуляции игры и копим статистику по ней.
Код для организации буфера памяти:
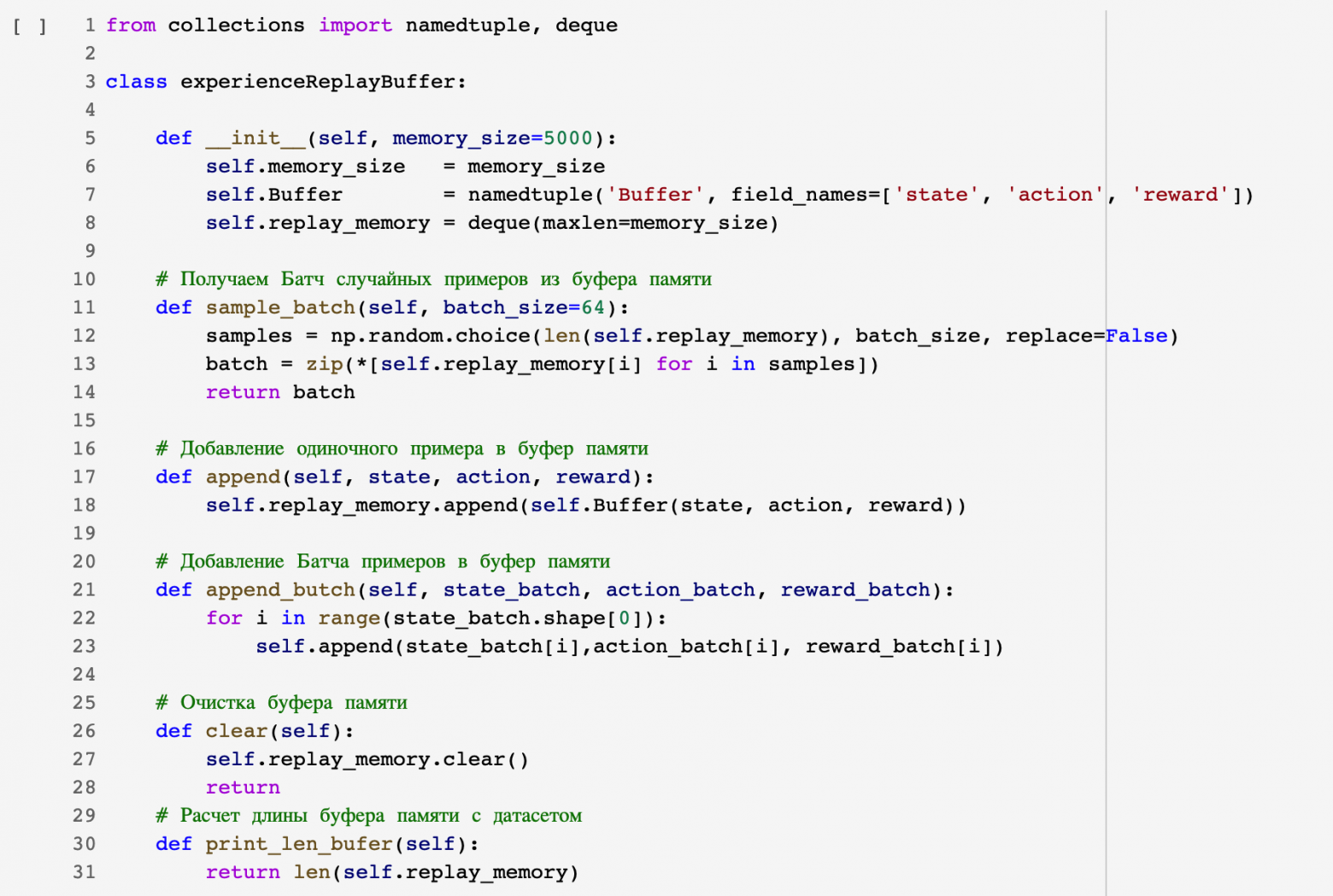
Проведя серию игр нашего Агента со Средой и накопив статистику мы можем переходить к обучению Агента.
Для этого мы из буфера памяти с накопленной статистикой получаем батч наших данных в виде троек значений, распаковываем и преобразуем в тензоры Pytorch.

Батч состояний среды в виде тензора Pytorch подаем на вход на нейросети агента, получаем распределение вероятностей для каждого хода агента для каждого состоянии среды в матче, логарифмируем эти вероятности, умножаем на награду полученную агентом за ход на логарифм этих вероятностей, затем берем среднее по произведениям и делаем это среднее отрицательным:
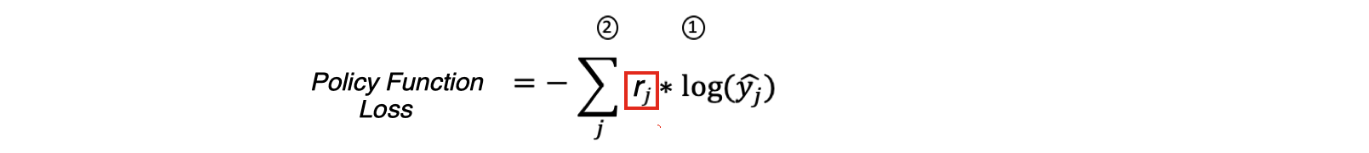
Этап 1

Этап 2

После того как мы получили значение Loss функции мы делаем обратный проход по нейросети, чтобы получить градиенты и делаем шаг оптимайзером для корректировки весов. На этом цикл обучения нашего агента закачивается.
Так как после того как оптимайзер сдвинул веса нейросети наши данные в собранные в статистике уже не являются актуальными, потому что нейросеть со сдвинутыми весами будет выдавать совершенно другие вероятности для действий по этим же состояниям среды и обучение агента дальше пойдет неправильно.
По этому мы очищаем наш буфер с памятью, проигрываем снова определенное количество игр для сбора статистики и вновь запускаем процесс обучения агента.
Это и есть петля обучения при обучении без учителя методом Policy Gradient.
- Накопление статистических данных
- Обучение Агента
- Сброс статистических данных
Процесс обучения повторяем столько раз, пока наш Агент не научится получать от системы ту награду которая нас устраивает.
Глава 9. Эксперименты с Агентом и Средой
Запустим серию экспериментов по обучению нашего Агента.
Для экспериментов выберем следующие параметры среды:

Для Агента выберем — сконструируем нейросеть — она будет сверточной (т.к. работаем с изображением) на выходе у нее будет 9 выходов (1-вправо, 2-влево, 3-вверх, 4-вниз, 5-вправо-вверх, 6-влево-вверх, 7-вправо-вниз, 8-влево-вниз, 9-ничего не делать) и SoftMax, чтобы получать вероятность для каждого действия.
Архитектура нейросети
Первый Conv2d слой 32 нейрона размер изображения 1*32*16
MaxPool2d слой размер изображения 32*16*8
Второй Conv2d слой 32 нейрона размер изображения 32*16*8
MaxPool2d слой размер изображения 32*8*4
Flatten — выпрямляем изображение в размер 1024
Linear слой на 1024 нейрона
Dropout(0.25) слой
Linear слой на 512 нейронов
Linear слой на 256 нейронов
Linear слой на 9 нейронов и SoftMax
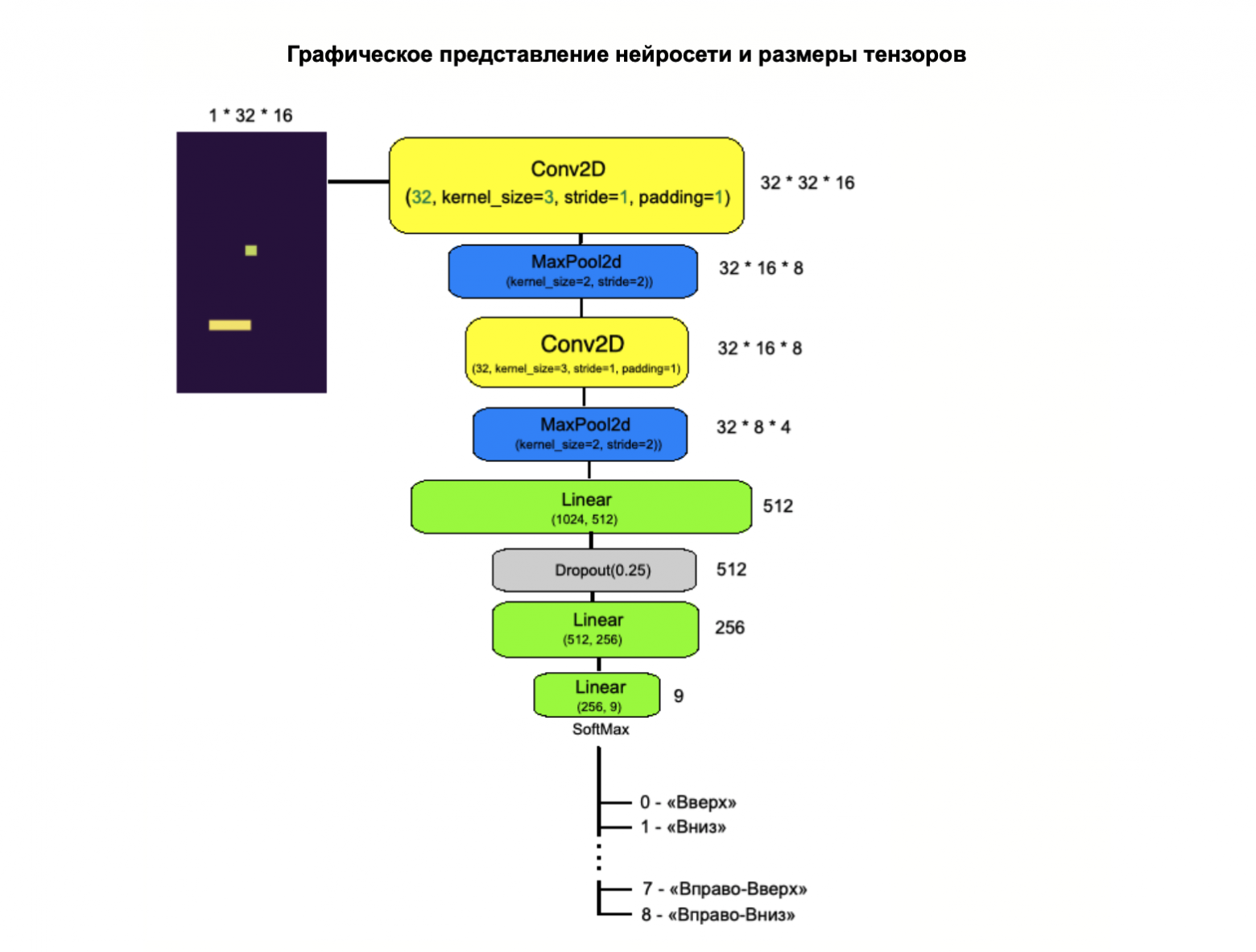
Код создания нейросети на Pytorch

Поочередно запустим три цикла обучения Агента в Среде параметры которых разобрали выше:
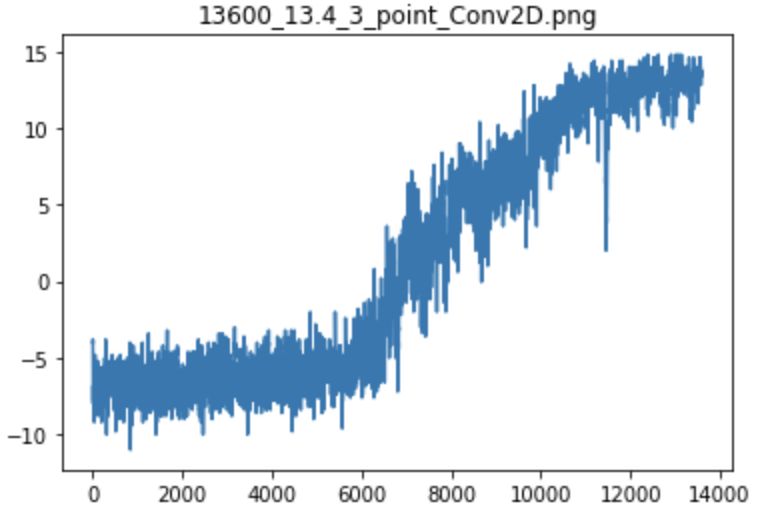
Эксперимент № 1 — Агент научился решать задачу за 13600 циклов игры
Начальное состояние Агента

График тренировки Агента
Обученное состояние Агента

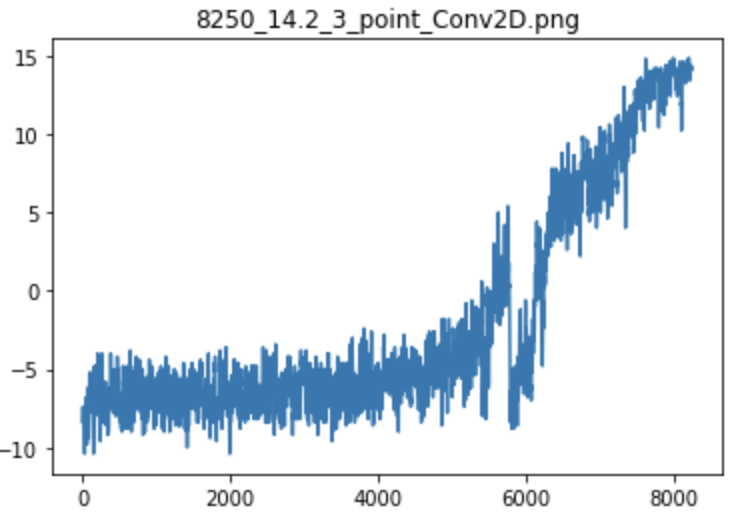
Эксперимент № 2 — Агент научился решать задачу за 8250 циклов игры
Начальное состояние Агента

График тренировки Агента
Обученное состояние Агента

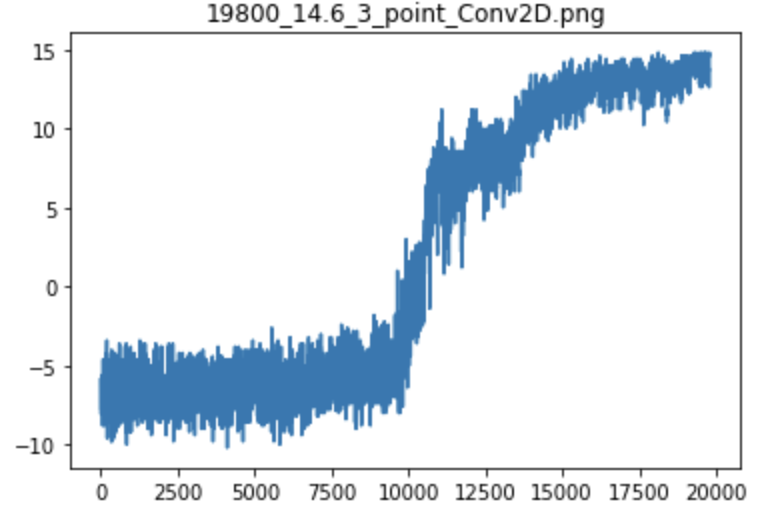
Эксперимент № 3 — Агент научился решать задачу за 19800 циклов игры
Начальное состояние Агента

График тренировки Агента
Обученное состояние Агента

Глава 10. Выводы
Глядя на графики можно сказать, что обучение Агента конечно происходит медленно.
Агент изначально довольно долго ищет хоть какую-то разумную политику для своих действий, чтобы начать получать положительную награду.
В это время на первом этапе графика, идет медленное нарастание награды за игру, потом внезапно Агент находит удачный вариант для своих ходов, и награда полученная им за игру круто увеличивается вверх и идет по нарастающей, а затем приблизившись к максимуму награды, у агента опять идет медленное увеличение эффективности, когда он совершенствует уже выученную им политику ходов, но стремясь как и любой жадный алгоритм забрать награду себе полностью.
Также хочется отметить большую потребность в вычислениях для обучения Агента методом Policy Gradient, т.к. основное время работы алгоритма происходит набор статистики ходов Агента а не его обучение. Набрав статистику по ходам из всего массива мы используем только один батч данных для обучения Агента, а все остальные данные выбрасываем, как уже непригодные к обучению. И опять собираем новые данные.
Можно еще много экспериментировать с данным алгоритмом и средой — изменяя глубину и ширину колодца, увеличивая или уменьшая количество кубиков падающих за игру, делая эти кубики разного цвета. Чтобы пронаблюдать какое это влияние окажет на эффективность и скорость обучения Агента.
Также обширное поле для экспериментов — параметры нейросети, по сути нашего Агента которого мы и обучаем, можно менять слои, ядра свертки, включать и подстраивать регуляризацию. Да и много чего еще другого можно пробовать, чтобы повысить эффективность обучения Агента.
Таким образом запустив на практике эксперименты с обучением без учителя по методу Policy Gradient мы убедились, что обучение без учителя имеет место быть, и оно реально работает.
Агент самостоятельно обучился максимизировать свою награду в игре.
Ссылка на GitHub c кодом, адаптированным под работу в ноутбуке Google Colab
