How to become an author

ibessonov Nov 26 2023 at 23:09

Какова вероятность найти слово fuck в случайной последовательности из 20 букв?

Medium

20 min

12K

Entertaining tasksProgramming*Algorithms*Mathematics*

Однажды на работе возник вопрос — насколько вероятно, что в случайно сгенерированном идентификаторе (отдаваемом пользователю, к примеру) вдруг обнаружится плохое слово. Приблизительная оценка была дана достаточно быстро, а вот точное решение — уже не так тривиально.

Я решил всерьёз выяснить, чему равна эта вероятность в зависимости от длины случайной строки? Можно ли получить явную математическую формулу для ответа? Что, если взять другое слово? Что, если взять другой алфавит?

Обо всём по порядку.

1. Метод Монте-Карло

Что может быть легче? Генерируем миллионы — миллиарды! — случайных строк и проверяем, содержат ли они искомое слово.
Метод очень прост в реализации. Программа, перебирающая случайные строки в течение 30 секунд, для параметров из заголовка выдала ответ примерно $inline$ . Позже мы увидим, насколько он близок к точному значению.

Тут есть проблема, которая должна быть очевидна: метод Монте-Карло по времени вычисления является самым затратным из описанных в статье и сходится очень медленно. Это особенно хорошо видно, когда нужно получить точность порядка 8-9 знаков после запятой.
Зачем такая точность, спрашиваете? Чтобы была!

На задачи обозначенного размера даже 30 миллисекунд процессорного времени тратить не хочется, не то что просто секунд. Решение, пусть и универсальное, совершенно не годится.

2. Приблизительное решение

Второй вариант, который приходит на ум: быстро подобрать простую формулу и надеяться на то, что она даст хорошую аппроксимацию.

Вопрос: какой может быть позиция подстроки fuck внутри строки из 20-ти символов? Ответ: от 0 до 16, т.е. 17 различных вариантов. Для каждой такой позиции i, существует $26^{16}$ различных слов, в которых fuck — на i-й позиции (т.е. все возможные комбинации оставшихся 16-ти букв в строке).

Приняв к сведению, что некоторые слова мы посчитаем несколько раз (те, в которых fuck содержится более одного раза), можно сказать, что слов, содержащих fuck, будет точно меньше, чем $17\cdot26^{16}$ , а вероятность, соответственно, не превысит $17\cdot\frac{26^{16}}{26^{20}}$ (в знаменателе — количество всех возможных слов длины 20).

Это значение равно $\frac{17}{456976}$ , или приблизительно $inline$ .

3. Поиск точной формулы

3.1. Рекуррентное соотношение

Все последующие рассуждения будут касаться формул или процедур для получения точного ответа. Очевидно, что подходов может быть множество. Предлагаю начать с простейшей более-менее общей формулировки. Есть английский алфавит из 26 букв, найти количество слов длины $inline$ , содержащих в себе последовательность букв fuck хотя бы один раз.

Обозначим такое количество за $inline$ . Начинается последовательность безобидно:

$display$

Строки короче 4-х символов точно не содержат нужное подслово, а среди строк из 4-х символов есть только один подходящий кандидат — сама строка fuck. Достаточно быстро значения становятся менее упорядоченными:

$C_4(5)=2\cdot26, C_4(6)=3\cdot26^2, C_4(7)=4\cdot26^3, C_4(8)=5\cdot26^4-1, \ldots$

Тут всё ещё видна некая закономерность, но она очень быстро сломается, гарантирую.

Попробуем рассмотреть, как же значение с большими $inline$ зависит от значений с меньшими $inline$ . Допустим, что $inline$ . Предлагаю пересчитывать строки следующим способом:

Если префикс длины $inline$ уже содержит искомое слово, то выбор последней буквы ни на что не влияет, т.е. мы бесплатно получаем $26 \cdot C_4(n - 1)$ строк.
Если строка оканчивается на fuck, то первые $inline$ букв значения не имеют. Итого добавляется ещё $26 ^ {n - 4}$ строк.
Других вариантов быть не может: слово fuck встречается либо в конце, либо не в конце, но есть проблема — часть строк посчитаны дважды. В частности, те, которые оканчиваются на fuck и содержат его более, чем один раз (afuckafuck).
Нетрудно понять, что это единственный вид исключений. И все такие строки обязательно содержат fuck среди первых $inline$ символов, это значение мы и должны отнять как дважды посчитанное.

Итого, объединив все рассуждения, приходим к рекуррентному соотношению:

$C_4(n) = 26 \cdot C_4(n - 1) + 26^{n - 4} - C_4(n - 4)$

Стоит заметить, что с таким же удобством можно было бы рассматривать величины $inline$ , которые являлись бы не количеством, а вероятностью, или, точнее, пропорцией количества искомых строк с количеством всех возможных строк длины $inline$ . В новых терминах формула примет следующий вид. На мой взгляд, стало намного лучше:

$p_4(n) = p_4(n - 1) + \frac{1 - p_4(n - 4)}{26^ 4}$

Код для подобного соотношения будет тривиальным. Ответ для слов длины 20 равен $inline$ . Видно, что реальное значение отличается от ответа, полученного методом Монте-Карло, уже на 7-м знаке после запятой ( $inline$ ), а если отбросить нули, то и вовсе в третьей значащей цифре.
Простая аппроксимация ( $inline$ ) показала себя значительно лучше, дав ошибку лишь в 9-м знаке после запятой (пятой значащей цифре).

Рекуррентная формула — это хорошо, но явная формула — лучше, хочется и её найти.

Помимо этого, сложность процедуры вычисления рекуррентного соотношения является $inline$ , что не является оптимальной трудоёмкостью для данной задачи. Её обязательно нужно понизить.

3.2. Явная формула

На самом деле, задача очень даже типовая. Хорошо известно, как получить явную формулу для подобного класса задач, пусть и совсем не очевидно, почему надо поступать именно так. Но этот вопрос мы опустим, лучше найдём формулу.

В первую очередь забываем о начальном условии $inline$ на какое то время.
Напомню исходную рекуррентную формулу, слегка её обобщив, чтобы она была сейчас перед глазами. За $inline$ я обозначил значение $\frac{1}{26 ^ 4}$ , чтобы не делать последующие выражения ещё более громоздкими.

$p_4(n) = p_4(n - 1) + k - k \cdot p_4(n - 4)$

Для начала нужно найти частное решение, почти как в дифференциальных уравнениях. К счастью, оно лежит на поверхности: $p_4(n) \equiv 1$ . Действительно, подставив $inline$ в уравнение получим, что обе части тождественно равны.

Зная частное решение, само уравнение можно немного упростить. Положим $inline$ и попробуем искать ответ относительно $inline$ :

$q(n) = q(n - 1) - k \cdot q(n - 4)$

Перенеся всё в одну сторону, получим:

$q(n) - q(n - 1) + k \cdot q(n - 4) = 0$

Далее делается знаменитый финт ушами и предполагается, что есть возможность найти решение в виде $q(n) = \mu^n$ для некоего значения $\mu$ . Думаю многим читателям данный финт может быть знаком из вывода общей формулы для членов Фибоначчи, но работает он для любой линейной рекуррентной последовательности. Подставим:

$\mu^n - \mu^{n - 1} + k \cdot \mu^{n - 4} = 0$

Сократив это выражение на $\mu^{n - 4}$ , получим уравнение четвёртой степени:

$\mu^4 - \mu^3 + k = 0$

Это уравнение называется "характеристический многочлен", и у него есть 4 различных корня:

Спасибо, Wolfram|Alpha

Очень надеюсь, что я правильно скопировал ответ:
$\mu_1 = \frac{1}{4} -\frac{1}{2} \sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}\\ -\frac{1}{2} \sqrt{\Bigg(- \frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} - \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}}\\ - \frac{1}{4\sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}} + \frac{1}{2} \Bigg)}$

$\mu_2 = \frac{1}{4} -\frac{1}{2} \sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}\\ +\frac{1}{2} \sqrt{\Bigg(- \frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} - \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}}\\ - \frac{1}{4\sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}} + \frac{1}{2} \Bigg)}$

$\mu_3 = \frac{1}{4} +\frac{1}{2} \sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}\\ -\frac{1}{2} \sqrt{\Bigg(- \frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} - \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}}\\ + \frac{1}{4\sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}} + \frac{1}{2} \Bigg)}$

$\mu_4 = \frac{1}{4} +\frac{1}{2} \sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}\\ +\frac{1}{2} \sqrt{\Bigg(- \frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} - \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}}\\ + \frac{1}{4\sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}} + \frac{1}{2} \Bigg)}$

Несложно убедиться, что если $q_1(n)=\mu_1^n$ и $q_2(n)=\mu_2^n$ — решения, то и $a \cdot q_1(n) + b \cdot q_2(n)$ — тоже решение, где $inline$ и $inline$ — произвольные константы. Т.е. решение в общем виде выглядит так:

$p_4(n) = a\mu_1^n + b\mu_2^n + c\mu_3^n + d\mu_4^n + 1$

Значения $inline$ , $inline$ , $inline$ и $inline$ следует искать из начальных условий:

$\left\{ \begin{array} &p_4(0) = a &+\ b &+\ c &+\ d &+\ 1 &= 0\\ p_4(1) = a\mu_1 &+\ b\mu_2 &+\ c\mu_3 &+\ d\mu_4 &+\ 1 &= 0\\ p_4(2) = a\mu_1^2 &+\ b\mu_2^2 &+\ c\mu_3^2 &+\ d\mu_4^2 &+\ 1 &= 0\\ p_4(3) = a\mu_1^3 &+\ b\mu_2^3 &+\ c\mu_3^3 &+\ d\mu_4^3 &+\ 1 &= 0\\ \end{array} \right.$

Решаем данную систему и подставляем результат в ответ, всё просто! Для этого воспользуемся методом Крамера, который выражает решения системы линейных уравнений через определители некоторых матриц. Выглядеть матрицы будут следующим образом:

$\Delta=\begin{vmatrix} 1 & 1 & 1 & 1 \\ \mu_1 & \mu_2 & \mu_3 & \mu_4 \\ \mu_1^2 & \mu_2^2 & \mu_3^2 & \mu_4^2 \\ \mu_1^3 & \mu_2^3 & \mu_3^3 & \mu_4^3 \\ \end{vmatrix}$

$\Delta_a=-\begin{vmatrix} 1 & 1 & 1 & 1 \\ 1 & \mu_2 & \mu_3 & \mu_4 \\ 1 & \mu_2^2 & \mu_3^2 & \mu_4^2 \\ 1 & \mu_2^3 & \mu_3^3 & \mu_4^3 \\ \end{vmatrix} \: \Delta_b=-\begin{vmatrix} 1 & 1 & 1 & 1 \\ \mu_1 & 1 & \mu_3 & \mu_4 \\ \mu_1^2 & 1 & \mu_3^2 & \mu_4^2 \\ \mu_1^3 & 1 & \mu_3^3 & \mu_4^3 \\ \end{vmatrix}$

$\Delta_c=-\begin{vmatrix} 1 & 1 & 1 & 1 \\ \mu_1 & \mu_2 & 1 & \mu_4 \\ \mu_1^2 & \mu_2^2 & 1 & \mu_4^2 \\ \mu_1^3 & \mu_2^3 & 1 & \mu_4^3 \\ \end{vmatrix} \Delta_d=-\begin{vmatrix} 1 & 1 & 1 & 1 \\ \mu_1 & \mu_2 & \mu_3 & 1 \\ \mu_1^2 & \mu_2^2 & \mu_3^2 & 1 \\ \mu_1^3 & \mu_2^3 & \mu_3^3 & 1 \\ \end{vmatrix}$

В данных терминах решения будут найдены в виде $a=\frac{\Delta_a}{\Delta}$ , $b=\frac{\Delta_b}{\Delta}$ , $c=\frac{\Delta_c}{\Delta}$ и $d=\frac{\Delta_d}{\Delta}$ .
Можно заметить, что каждый из определителей является определителем Вандермонда, для которого есть замечательная формула вычисления:

$\Delta = \prod\limits_{1\le j < i \le 4}(\mu_i - \mu_j) = (\mu_4 - \mu_3)(\mu_4 - \mu_2)(\mu_4 - \mu_1)(\mu_3 - \mu_2)(\mu_3 - \mu_1)(\mu_2 - \mu_1)$
$\Delta_a = -(\mu_4 - \mu_3)(\mu_4 - \mu_2)(\mu_4 - 1)(\mu_3 - \mu_2)(\mu_3 - 1)(\mu_2 - 1)$
$\Delta_b = -(\mu_4 - \mu_3)(\mu_4 - 1)(\mu_4 - \mu_1)(\mu_3 - 1)(\mu_3 - \mu_1)(1 - \mu_1)$
$\Delta_c = -(\mu_4 - 1)(\mu_4 - \mu_2)(\mu_4 - \mu_1)(1 - \mu_2)(1 - \mu_1)(\mu_2 - \mu_1)$
$\Delta_d = -(1 - \mu_3)(1 - \mu_2)(1 - \mu_1)(\mu_3 - \mu_2)(\mu_3 - \mu_1)(\mu_2 - \mu_1)$

Поделив определители друг на друга, получим симпатичный ответ:

$\left\{ \begin{array} &a=-\frac{(1-\mu_2)(1-\mu_3)(1-\mu_4)}{(\mu_1-\mu_2)(\mu_1-\mu_3)(\mu_1-\mu_4)}\\ b=-\frac{(1-\mu_1)(1-\mu_3)(1-\mu_4)}{(\mu_2-\mu_1)(\mu_2-\mu_3)(\mu_2-\mu_4)}\\ c=-\frac{(1-\mu_1)(1-\mu_2)(1-\mu_4)}{(\mu_3-\mu_1)(\mu_3-\mu_2)(\mu_3-\mu_4)}\\ d=-\frac{(1-\mu_1)(1-\mu_2)(1-\mu_3)}{(\mu_4-\mu_1)(\mu_4-\mu_2)(\mu_4-\mu_3)} \end{array} \right.$

Т.е. $p_4(n)=1 - \frac{\mu_1^n(1-\mu_2)(1-\mu_3)(1-\mu_4)}{(\mu_1-\mu_2)(\mu_1-\mu_3)(\mu_1-\mu_4)} - \frac{\mu_2^n(1-\mu_1)(1-\mu_3)(1-\mu_4)}{(\mu_2-\mu_1)(\mu_2-\mu_3)(\mu_2-\mu_4)}\\ - \frac{\mu_3^n(1-\mu_1)(1-\mu_2)(1-\mu_4)}{(\mu_3-\mu_1)(\mu_3-\mu_2)(\mu_3-\mu_4)} - \frac{\mu_4^n(1-\mu_1)(1-\mu_2)(1-\mu_3)}{(\mu_4-\mu_1)(\mu_4-\mu_2)(\mu_4-\mu_3)}$

4. Поиск эффективной процедуры вычисления

4.1. Регулярный язык

Данный конкретный случай со словом длиной 4 решён в явном виде. Но, помимо математической красоты, практической ценности он не имеет. При словах длиной больше, чем 4, степень характеристического многочлена будет увеличиваться. Так как уравнения степени выше четвёртой не имеют формулы для их решения, то с нахождением соответствующих значений $\mu$ могут возникнуть серьёзные проблемы (хотя Wolfram|Alpha и способен выдать решения соответствующего уравнения 5-й степени через обобщённые гипергеометрические функции, я понятия не имею, что это такое). Конечно, можно попробовать решать их численно, но это как-то слишком сложно для такой простой задачи.

К слову, пусть и не всегда можно явно вычислить корни характеристического многочлена, все рассуждения можно почти дословно повторить для всех $p_m(n) = p_m(n - 1) + k - k \cdot p_m(n - m)$ , соответствующих "простым" искомым словам длины $inline$ . Что я имею ввиду под "простыми" словами, будет объяснено ближе к концу статьи, не всё сразу.

Не думаю, что можно выжать ещё какие-то интересные факты из решения с помощью рекуррентной формулы, так что будем использовать другой подход. К математике вернёмся попозже.

Поговорим о регулярных языках. Строки, содержащие подстроку fuck, описываются регулярным выражением ^.*fuck.*$ (пользуясь синтаксисом для языка Java). Эквивалентный способ описания регулярных языков, на практике менее привычный — это конечные автоматы. В частности, детерминированные конечные автоматы (ДКА). Они сложнее в построении, но проще в обработке. ДКА для описания языка, все слова которого содержат подслово fuck, выглядит следующим образом:

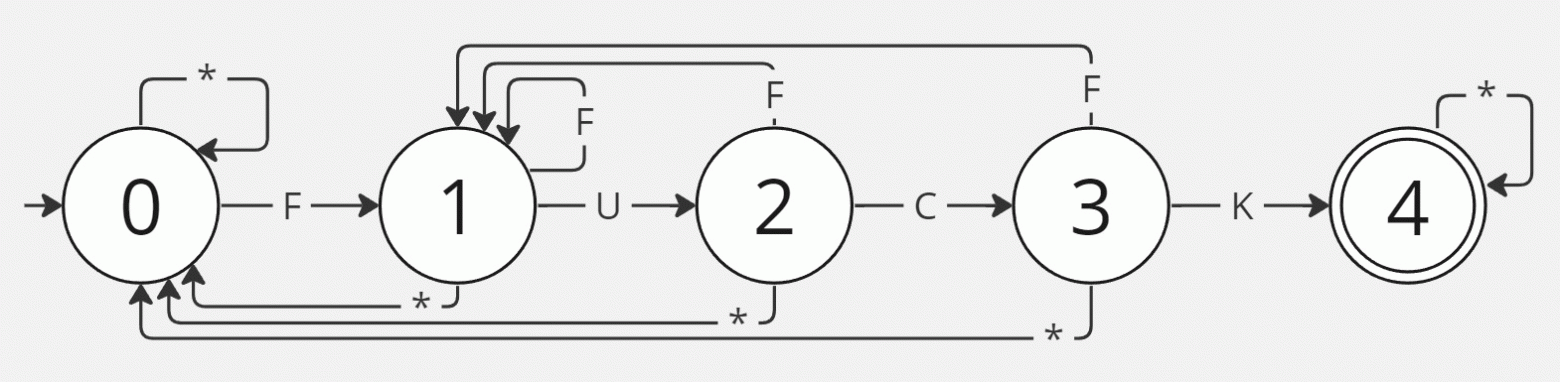
Переходы, помеченные звёздочкой, фактически означают "ветку else" — все оставшиеся символы, которые не встречаются в явно помеченных переходах.

Состояние $inline$ — начальное, $inline$ — завершающее, все остальные — промежуточные. Видно, что данный конечный автомат не только детерминированный, но и полный, т.е. для каждого состояния и каждого символа алфавита определена функция перехода (существует выходящее ребро графа с соответствующей меткой). Это важно и понадобится в будущем.

Наделим состояния автомата осязаемым смыслом, начиная с последнего.

$inline$ — на текущий момент уже найдено подслово fuck и все оставшиеся символы просто пропускаются с помощью перехода из завершающего состояния в него же.
$inline$ — на текущий момент прочитан префикс, заканчивающийся на fuc. Есть два возможных варианта — либо дальше идёт k и можно переходить в завершающее состояние, либо там другой символ и поиск нужно "начинать сначала", т.е. идти либо в $inline$ если увидели f, либо идти вообще в начальное состояние $inline$ .
$inline$ — на текущий момент прочитан префикс, заканчивающийся на fu. Есть два возможных варианты — либо дальше идёт символ c, удлиняющий текущий найденный префикс слова fuck, либо какой-то другой символ, не позволяющий увеличить прочитанный префикс и заставляющий нас идти либо в $inline$ , либо в $inline$ .
...

Не хочется ещё несколько раз повторять ту же самую идею. Важно вот что — состояние $inline$ означает, что в момент нахождения в нём мы уже вычитали префикс, совпадающий с префиксом длины $inline$ строки fuck.

Далее я предлагаю отождествлять префиксы искомого слова с названиями состояний соответствующего конечного автомата. Перерисую его с учётом новых названий:

Как по конечному автомату понять, сколько слов длины $inline$ он сможет распознать? В общем случае этот вопрос может показаться сложным, но точно не для полных ДКА. Ведь для них поиск количества слов сводится к поиску в графе количества путей фиксированной длины из одной вершины к другой (из начального состояния в конечное).

4.2. Исследование конечного автомата

Обозначим за $L_{i, j}^{(n)}$ количество различных путей длины $inline$ из состояния $inline$ в состояние $inline$ и исследуем свойства получившихся величин.

Воспользуемся математической индукцией. $L_{i, j}^{(1)}$ — это просто число рёбер графа, ведущих из состояния $inline$ в состояние $inline$ , и вычисляется напрямую из описания конечного автомата.

Далее, допустим, что мы умеем вычислять все $L_{i, j}^{(n)}$ для какого-то $n \ge 1$ . Найдём $L_{i, j}^{(n+1)}$ .
Любой путь длины $inline$ неизбежно разбивается на начало пути длиной $inline$ и последним переходом длиной $inline$ . Причём "предпоследним" состоянием может быть совершенно любая вершина графа, обозначим её $inline$ .
Для каждой такой вершины число слов, проходящих сквозь неё на предпоследнем шаге, будет равно $L_{i, t}^{(n)} \cdot L_{t, j}^{(1)}$ . То есть произведение количества путей длины n на количество последующих путей длины 1 (количество соответствующих рёбер).

Взяв в расчёт все вершины $inline$ , приходим к формуле $L_{i, j}^{(n+1)} = \sum\limits_{t}(L_{i, t}^{(n)} \cdot L_{t, j}^{(1)})$ . Более того, проведя абсолютно те же самые рассуждения, можно получить формулу $L_{i, j}^{(n+r)} = \sum\limits_{t}(L_{i, t}^{(n)} \cdot L_{t, j}^{(r)})$ . Не то, что бы это было необходимо, скорее, помогает заметить закономерность.

Ничего не напоминает? Это один в один формулы для умножения матриц! Построим матрицу $inline$ в соответствии со значениями $L_{i, j}^{(1)}$ :

$L_m= \begin{pmatrix} L_{0,0}^{(1)} & L_{0,1}^{(1)} & \dots \\ \vdots & \ddots & \\ L_{m,0}^{(1)} & & L_{m,m}^{(1)} \end{pmatrix}$

Если использовать текущие обозначения, получим следующее общее выражение:

$L_m^n = \begin{pmatrix} L_{0,0}^{(1)} & L_{0,1}^{(1)} & \dots \\ \vdots & \ddots & \\ L_{m,0}^{(1)} & & L_{m,m}^{(1)} \end{pmatrix}^n = \begin{pmatrix} L_{0,0}^{(n)} & L_{0,1}^{(n)} & \dots \\ \vdots & \ddots & \\ L_{m,0}^{(n)} & & L_{m,m}^{(n)} \end{pmatrix}$

Симпатично вышло. Тем самым становится видно, что вычисление количества путей длины $inline$ сводится к возведению матрицы в степень $inline$ . Напомню, что данная формула применима к любому регулярному языку, если известен полный ДКА, который его описывает.

Матрицу $inline$ будем называть матрицей смежности. Для конкретного описанного ранее графа она выглядит следующим образом:

$L_{fuck} = \begin{pmatrix} 25 & 1 & 0 & 0 & 0 \\ 24 & 1 & 1 & 0 & 0 \\ 24 & 1 & 0 & 1 & 0 \\ 24 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 26 \end{pmatrix}$

Здесь видна явная закономерность в распределении единиц. Эта закономерность сохранится для более длинных "простых" слов:

$L_{hello} = \begin{pmatrix} 25 & 1 & 0 & 0 & 0 & 0 \\ 24 & 1 & 1 & 0 & 0 & 0 \\ 24 & 1 & 0 & 1 & 0 & 0 \\ 24 & 1 & 0 & 0 & 1 & 0 \\ 24 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 26 \end{pmatrix}$

Что же касается вычисления количества слов — оно равно количеству путей из единственного начального в единственное конечное состояние, т.е. $L_{0, m}^{(n)}$ . Если же возвращаться к изначальным обозначениям, то $C_m(n) = L_{0, m}^{(n)}$ для соответствующей матрицы $inline$ .
Т.к. вероятности мы выражали через $p_m(n) = \frac{C_m(n)}{26^n}$ , то новая формула для них будет выглядеть так:

$p_m(n) = \Big(\Big(\frac{L_m}{26}\Big)^n\Big)_{0, m}$

Понимаю, что очень много различных обозначений, но я просто не могу остановиться! Матрицу $\frac{L_m}{26}$ можно обозначить $inline$ . Она содержит не число путей из одного состояния в другое, а "вероятность перехода". Фактически она описывает однородную Цепь Маркова, соответствующую случайному блужданию по состояниям нашего графа с равномерной вероятностью выбора следующего ребра. Про цепи Маркова можно было вспомнить раньше, но да ладно.

4.3. Про возведения в степень

Теперь хотелось бы быстренько оценить трудоёмкость вычисления с помощью матриц. Для вычисления с помощью рекуррентного соотношения временная сложность была бы $inline$ .

Что же для матриц? Наивное итеративное возведение в степень дало бы $inline$ , а это хуже предыдущего результата. К счастью, возведение в степень за линейное время никто не осуществляет, ведь есть следующее правило:

$\left\{ \begin{array} &P_m^k = P_m^{k-1} \cdot P_m, & k = 2r + 1\\ P_m^k = (P_m^{k/2})^2, & k = 2r \end{array} \right.$

Подобный трюк позволяет понизить количество умножений до $O(\log(n))$ , тем самым давая общую трудоёмкость в $O(m^3 \log(n))$ — очень даже годится для практических вычислений.

Можно ещё кое-что сказать о возведении матриц в какие-нибудь степени. Согласно теореме Жордана, матрицу $inline$ можно представить в виде $P_m=C_mJ_mC_m^{-1}$ , где $inline$ — какая-то обратимая матрица, а $inline$ — Жорданова матрица, т.е. матрица, состоящая из Жордановых клеток. В частности, для случая простых слов типа fuck $inline$ — это диагональная матрица, содержащая на диагонали собственные числа матрицы $inline$ .

$J_m = \begin{pmatrix} \lambda_0 & \dots & 0\\ \vdots & \ddots & \\ 0 & & \lambda_m \end{pmatrix}$

Для доказательства этого факта достаточно показать, что у матрицы $inline$ нет повторяющихся собственных чисел. Можете попробовать сделать это самостоятельно (характеристический многочлен будет дан через несколько абзацев).

Жорданова форма облегчает возведение матриц в степени, в частности,

$P_m^n = (C_mJ_mC_m^{-1})^n = C_mJ_mC_m^{-1} \cdot C_mJ_mC_m^{-1} \dots C_mJ_mC_m^{-1} = C_m J_m^n C_m^{-1}$

Возведение в степень диагональной матрицы — задача тривиальная:

$J_m^n = \begin{pmatrix} \lambda_0^n & \dots & 0\\ \vdots & \ddots & \\ 0 & & \lambda_m^n \end{pmatrix}$

К чему я всё это? Взглянем на характеристический многочлен матрицы $P_{fuck}$ :

$\chi(P_{fuck}) = \det(P_{fuck} - \lambda E) = Const*(1-\lambda)(\lambda^4-\lambda^3+\frac{1}{26^4})$

Должно выглядеть знакомо. И ведь действительно — $\mu_i$ из явной формулы являются корнями данного уравнения, вдобавок к этому есть дополнительный корень $\lambda_0=1$ .

Если же попробовать символьно перемножить матрицы $inline$ , $inline$ и $C_m^{-1}$ , то можно получить то же самое выражение, что и раньше:

$p_4(n)=(P_{fuck}^n)_{0, 4} = 1 + a\lambda_1^n + b\lambda_2^n + c\lambda_3^n + d\lambda_4^n$

Как найти характеристический многочлен данной матрицы. Читать необязательно.

Чтобы упросить дальнейшие формулы, уменьшив в них число делений, лучше рассмотрим характеристический многочлен матрицы $inline$ , имеющей $inline$ строк/столбцов и соответствующей "простому" слову длины $inline$ .

$\chi(L_m) = \det(L_m-\lambda E) = \begin{vmatrix} 25-\lambda & 1 & 0 & \dots & 0 & 0 & 0 \\ 24 & 1-\lambda & 1 & \dots & 0 & 0 & 0 \\ 24 & 1 & -\lambda & \dots & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 24 & 1 & 0 & \dots & -\lambda & 1 & 0 \\ 24 & 1 & 0 & \dots & 0 & -\lambda & 1 \\ 0 & 0 & 0 & \dots & 0 & 0 & 26-\lambda \end{vmatrix}$

Воспользуемся формулой разложения определителя по последнему столбцу, получим следующее:

$\chi(L_m) = (26-\lambda)\begin{vmatrix} 25-\lambda & 1 & 0 & \dots & 0 & 0 \\ 24 & 1-\lambda & 1 & \dots & 0 & 0\\ 24 & 1 & -\lambda & \dots & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 24 & 1 & 0 & \dots & -\lambda & 1 \\ 24 & 1 & 0 & \dots & 0 & -\lambda \end{vmatrix} - 1\begin{vmatrix} 25-\lambda & 1 & 0 & \dots & 0 & 0 \\ 24 & 1-\lambda & 1 & \dots & 0 & 0 \\ 24 & 1 & -\lambda & \dots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 24 & 1 & 0 & \dots & -\lambda & 1 \\ 0 & 0 & 0 & \dots & 0 & 0 \end{vmatrix}$

У матрицы во втором слагаемом последняя строка полностью заполнена нулями, а, значит, и определитель этой матрицы равен нулю. То есть, про второе слагаемое можно забыть. Помним, что матрица в первом слагаемом теперь имеет $inline$ строк и столбцов.

Снова произведём разложение определителя, на этот раз по первой строке. Получим

$\chi(L_m) = (26-\lambda)\left[(25-\lambda)\begin{vmatrix} 1-\lambda & 1 & \dots & 0 & 0 \\ 1 & -\lambda & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & 0 & \dots & -\lambda & 1 \\ 1 & 0 & \dots & 0 & -\lambda \end{vmatrix} - 1\begin{vmatrix} 24 & 1 & \dots & 0 & 0 \\ 24 & -\lambda & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 24 & 0 & \dots & -\lambda & 1 \\ 24 & 0 & \dots & 0 & -\lambda \end{vmatrix} \right]$

Теперь матрицы в обоих слагаемых имеют $inline$ строк и столбцов. Важно за этим следить.
Заметим, что во второй матрице можно вынести 24 из первого столбца. Первую же матрицу снова разложим по первой строке:

$\chi(L_m) = (26-\lambda)\left[(25-\lambda)\left( (1-\lambda)\begin{vmatrix} -\lambda & 1 & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \dots & -\lambda & 1 \\ 0 & 0 & \dots & 0 & -\lambda \end{vmatrix} - 1\begin{vmatrix} 1 & 1 & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & 0 & \dots & -\lambda & 1 \\ 1 & 0 & \dots & 0 & -\lambda \end{vmatrix} \right) - 24\begin{vmatrix} 1 & 1 & \dots & 0 & 0 \\ 1 & -\lambda & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & 0 & \dots & -\lambda & 1 \\ 1 & 0 & \dots & 0 & -\lambda \end{vmatrix} \right]$

Мы получили выражение, в котором содержатся только матрицы очень простой структуры. Обозначим их $inline$ и $inline$ и перепишем выражение в новых терминах. Нижний индекс для $inline$ и $inline$ — число строк в матрицах:

$\chi(L_m) = (26-\lambda)\left[(25-\lambda)\left( (1-\lambda)\det(A_{m-2}) - \det(B_{m-2}) \right) - 24\det(B_{m-1}) \right]$

Здесь я не буду расписывать всё настолько подробно. Матрица $inline$ — верхне-треугольная, её определитель равен $\det(A_k) = (-\lambda)^k$ .

С матрицей $inline$ немного сложнее. Думаю, к этому моменту разложение определителя не должно вызывать проблем, поэтому сделаем его в уме (по первой строке):

$\det(B_k) = 1\cdot\det(A_{k-1}) - 1\cdot\det(B_{k-1}) = (-\lambda)^{k-1} - det(B_{k-1})$

Воспользовавшись математической индукцией (а потом формулой суммы геометрической прогрессии), несложно будет доказать, что

$\det(B_k) = (-1)^{k+1}(\lambda^{k-1} + \lambda^{k-2} + \dots + \lambda + 1) = (-1)^{k+1}\frac{\lambda^k - 1}{\lambda - 1}$

Подставив результаты в исходную формулу и упростив выражение несколько раз, получим

$\chi(L_m) = (26-\lambda)\left[(25-\lambda)\left( (1-\lambda)(-\lambda)^{m-2} - (-1)^{m-1}\frac{\lambda^{m-2} - 1}{\lambda - 1} \right) - 24(-1)^m\frac{\lambda^{m-1} - 1}{\lambda - 1} \right] \\ = (26-\lambda)\left[ (25-\lambda)(1-\lambda)(-\lambda)^{m-2} + (-1)^m(25-\lambda)\frac{\lambda^{m-2} - 1}{\lambda - 1} - 24(-1)^m(\lambda^{m-2} + \frac{\lambda^{m-2} - 1}{\lambda - 1}) \right] \\ = (26-\lambda)\left[ (25-\lambda)(1-\lambda)(-\lambda)^{m-2} - 24(-\lambda)^{m-2} + (-1)^m(25-\lambda - 24)\frac{\lambda^{m-2} - 1}{\lambda - 1}) \right] \\ = (-1)^m (26-\lambda)\left[ (25-\lambda)(1-\lambda)\lambda^{m-2} - 24\lambda^{m-2} - (\lambda^{m-2} - 1) \right] \\ = (-1)^m (26-\lambda)\left[ 25\lambda^{m-2} - 26\lambda^{m-1} + \lambda^m - 24\lambda^{m-2} - \lambda^{m-2} + 1 \right] \\ = (-1)^m (26-\lambda)\left[ \lambda^m - 26\lambda^{m-1} + 1 \right]$

То есть

$\chi(L_m) = (-1)^m (26-\lambda)\left[ \lambda^m - 26\lambda^{m-1} + 1 \right]$

Дальше всё понятно, нужно просто сделать замену переменной в получившейся формуле.

5. Общий случай

На протяжении статьи я употреблял фразу "простое слово", не давая ей точного определения. Постараюсь это исправить. Рассмотрим пример, пусть есть алфавит из трёх символов — {a, b, c}. Посчитаем все слова длиной 3, которые содержат подслово ab: aab, aba, abb, abc, bab и cab. Всего 6 слов из 27-ми.

Если же искать слово aa, то вариантов останется всего пять: aaa, aab, aac, baa и caa. То есть вероятность заметно понизилась.

На самом деле для слова aa предпосылки, на которых мы строили изначальную рекуррентную формулу, ломаются, и использовать эту формулу попросту нельзя.
А именно, ломается подсчёт количества слов, которые "заканчиваются на aa и содержат его более, чем один раз". В этом месте при выводе формулы мы неявно допустили, что у искомого слова нет суффикса, совпадающего с её префиксом. Для fuck свойство выполнено, а для aa — нет.

На примере строк похожей длины, предлагаю рассмотреть слово abab, у него как раз есть префикс ab, совпадающий с суффиксом:

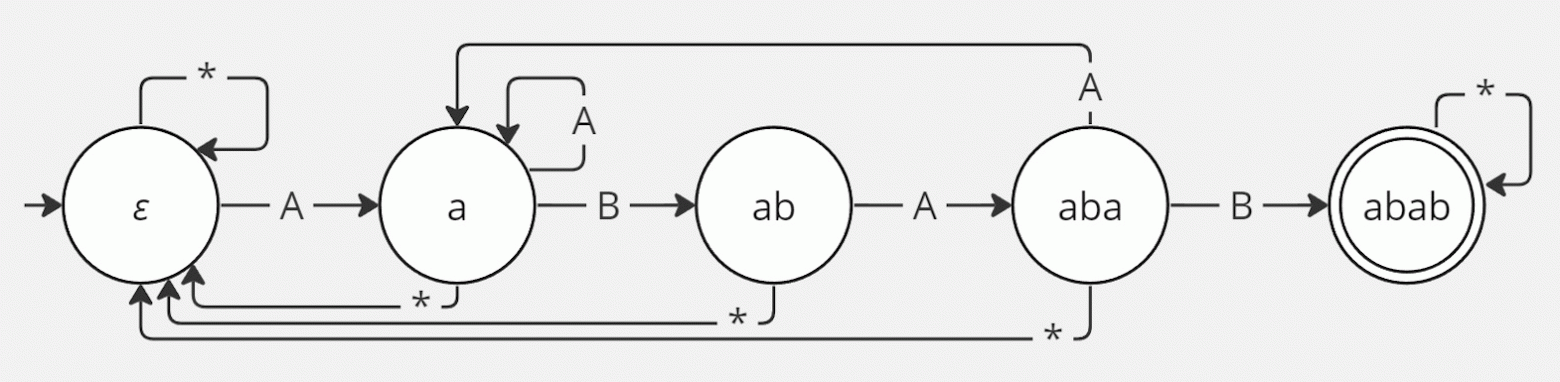
Матрица смежности для него, соответственно, тоже будет отличной. Имеющиеся ранее закономерности нарушены, да и характеристический многочлен другой (считать не буду, просто поверьте):

$L_{fuck} = \begin{pmatrix} 25 & 1 & 0 & 0 & 0 \\ 24 & 1 & 1 & 0 & 0 \\ 24 & 1 & 0 & 1 & 0 \\ 24 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 26 \end{pmatrix} \ L_{abab} = \begin{pmatrix} 25 & 1 & 0 & 0 & 0 \\ 24 & 1 & 1 & 0 & 0 \\ 25 & 0 & 0 & 1 & 0 \\ 24 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 26 \end{pmatrix}$

Казалось бы, совсем чуть-чуть отличается одна строка, а какой эффект. Получается, что эти матрицы отличаются достаточно сильно, чтобы ответы в итоге получались разные.

С другой стороны, есть слова, для которых рассуждения о рекуррентном соотношении всё ещё справедливы, но конечный автомат для которых тоже сильно отличается от исходного. Например, слово aaab:

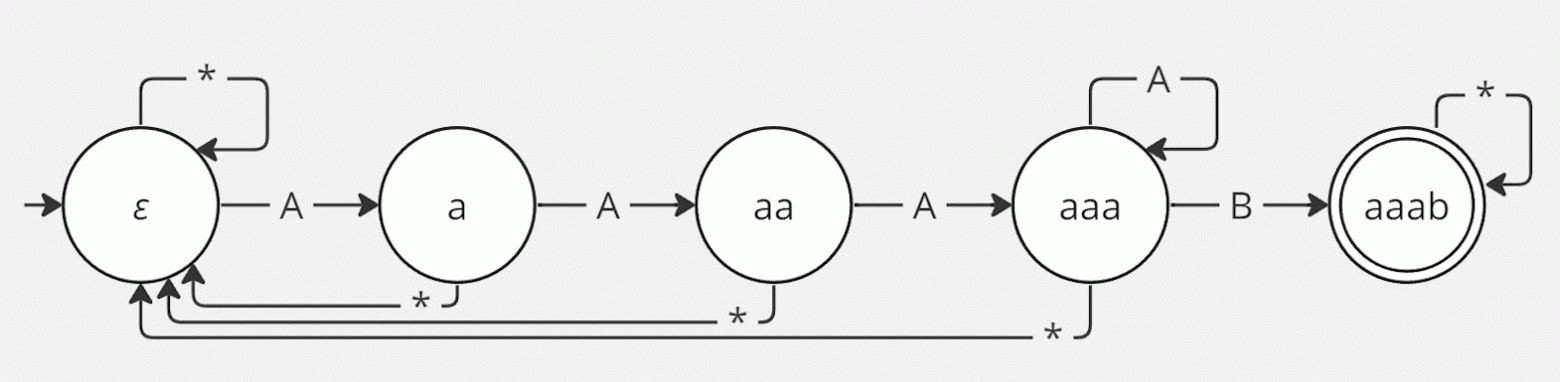
$L_{aaab} = \begin{pmatrix} 25 & 1 & 0 & 0 & 0 \\ 25 & 0 & 1 & 0 & 0 \\ 25 & 0 & 0 & 1 & 0 \\ 24 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 26 \end{pmatrix}$

Эта матрица отличается от обеих матриц, приведённых до неё, но всё равно приводит к ответу, совпадающему с таковым для слова fuck! Более того, совпадает не только ответ, но и характеристический многочлен. Матрицы $L_{fuck}$ и $L_{aaab}$ имеют одну и ту же Жорданову форму, и вот это уже совсем неочевидно по их внешнему виду.

Далее, помимо длины общего префикса/суффикса, на конечный ответ могут влиять и другие факторы. Например, есть ли у префикса/суффикса свой собственный, более короткий префикс/суффикс, и т.д.

Для получения истиной, общей процедуры получения ответа, проще всего построить для слова соответствующий конечный автомат, а по автомату — матрицу, и возводить её в нужную степень. Обобщение рекуррентного соотношения слишком сложно сделать.
Тут я уже не буду никого утомлять точным способом построения ДКА, что-то очень похожее есть, например, в алгоритме Ахо — Корасик. Тот же алгоритм поможет определить вероятность того, что в вашей строке есть нехорошее слово из заранее подготовленного словаря.

Заключение

Кажется, я не ответил на вопрос "Что, если взять другой алфавит?". Замените 26 на другое число, вот и всё.

Что в итоге. Интересную задачу посмотрели, математику младших курсов вспомнили, выводов особо не сделали. Моей целью было немного развлечь читателя и, может быть, показать что-то новое — надеюсь, было интересно. Думаю, наибольшую пользу из статьи смогут извлечь как раз-таки студенты. Код не привожу, да и стали бы вы его читать?

Спасибо за внимание!

Tags:

Hubs:

+55

Иван Бессонов @ibessonov

Математик, программист

Github Telegram

Show the best of all time