— Я ничего в ней не вижу, — сказал я, возвращая шляпу Шерлоку Холмсу.
— Нет, Уотсон, видите, но не даете себе труда поразмыслить над тем, что видите.
Артур Конан Дойл. Голубой карбункул
В предыдущей серии постов для начинающих (первый пост тут) из ремикса книги Генри Гарнера «Clojure для исследования данных» (Clojure for Data Science) на языке Python было представлено несколько численных и визуальных подходов, чтобы понять, что из себя представляет нормальное распределение. Мы обсудили несколько описательных статистик, таких как среднее значение и стандартное отклонение, и то, как они могут использоваться для краткого резюмирования больших объемов данных.
Набор данных обычно представляет собой выборку из некой более крупной популяции, или генеральной совокупности. Иногда эта популяция слишком большая, чтобы быть измеренной полностью. Иногда она неизмерима по своей природе, потому что она бесконечна по размеру либо потому что к ней нельзя получить непосредственный доступ. В любом случае мы вынуждены делать вывод, исходя из данных, которыми мы располагаем.
В этой серии из 4-х постов мы рассмотрим статистический вывод: каким образом можно выйти за пределы простого описания выборок и вместо этого описать популяцию, из которой они были отобраны. Мы подробно рассмотрим степени нашей уверенности в выводах, которые мы делаем из выборочных данных. Мы раскроем суть робастного подхода к решению задач в области исследования данных, каким является проверка статистических гипотез, которая как раз и привносит научность в исcледование данных.
Кроме того, по ходу изложения будут выделены болевые точки, связанные с терминологическим дрейфом в отечественной статистике, иногда затуманивающим смысл и подменяющим понятия. В конце заключительного поста можно будет проголосовать за или против размещения следующей серии постов. А пока же…
В целях иллюстрации принципов статистического вывода, мы создадим вымышленную компанию под названием AcmeContent, которая недавно наняла нас в качестве исследователей данных.
Представляем AcmeContent
Для оказания помощи в иллюстрировании понятий, представленных в этой серии постов, предположим, что в компанию AcmeContent нас недавно назначили в качестве исследователей данных. Компания заведует веб-сайтом, предлагающим своим посетителям возможность делиться между собой понравившимися им видеоклипами по Интернет.
Одна из метрик, которая отслеживается в AcmeContent посредством веб-аналитики — это время пребывания. Указанная метрика служит мерой количества времени, в течение которого посетитель остается на веб-сайте. Безусловно, посетителям, которые проводят на веб-сайте продолжительное время, веб-сайт нравится, и в AcmeContent хотели бы, чтобы посетители оставались на нем максимально долго.
Время пребывания (dwell time)— это отрезок времени между временем, прибытия посетителя на веб-сайт и временем, когда он сделал последний запрос.
Отскок (bounce) — это посетитель, который выполняет всего один запрос — его время пребывания равно нулю.
На вас, как новом исследователе данных, лежит в компании обязанность анализировать время пребывания посетителей на веб-сайте - этот показатель фигурирует в аналитических отчетах посещаемости веб-страниц и разделов веб-сайта - и измерять успех веб-сайта AcmeContent.
Загрузка и обследование данных
Здесь мы будем пользоваться теми же самыми библиотеками, что и ранее: scipy, pandas и matplotlib. В предыдущей серии постов мы использовали библиотеку pandas для загрузки электронных таблиц Excel, задействуя ее функцию read_excel. Здесь мы будем загружать набор данных из текстового файла с разделением значений символом табуляции. Для этого мы воспользуемся функцией pandas read_csv, которая на входе ожидает URL-адрес либо путь к файлу в строковом формате.
Файл был любезно переформатирован веб-командой AcmeContent и содержит всего два столбца — дату запроса и время пребывания на веб-сайте в секундах. Заголовки столбцов расположены в первой строке файла:
Названия приводимых примеров имеют формат ex_N_M, где ex - example (пример), N - номер серии постов и M - порядковый номер в посте. Примеры оформлены в виде функций без аргументов и возвращаемых значений. Это сделано намеренно, т.к. задачно-ориентированный стиль изложения требует кратких и четких примеров без отвлекающей внимание информации. К тому же, в таком виде примеры могут быть собраны вместе и исполняться независимо в рамках программной оболочки.
def load_data( fname ):
return pd.read_csv('data/ch02/' + fname, '\t')
def ex_2_1():
return load_data('dwell-times.tsv').head()Если выполнить этот пример (в консоли интерпретатора Python либо в блокноте Jupyter), то можно увидеть результат, который показан ниже:
date | dwell-time | |
0 | 2015-01-01T00:03:43Z | 74 |
1 | 2015-01-01T00:32:12Z | 109 |
2 | 2015-01-01T01:52:18Z | 88 |
3 | 2015-01-01T01:54:30Z | 17 |
4 | 2015-01-01T02:09:24Z | 11 |
… | … | … |
Посмотрим, как выглядит время пребывания на гистограмме.
Визуализация времени пребывания
Мы можем построить гистограмму времени пребывания, выбрав столбец dwell-time и применив к нему функцию hist:
def ex_2_2():
load_data('dwell-times.tsv')['dwell-time'].hist(bins=50)
plt.xlabel('Время пребывания, сек.')
plt.ylabel('Частота')
plt.show() Приведенный выше пример сгенерирует следующую ниже гистограмму:

Очевидно, что эти данные не являются нормально распределенными; они даже не представляют собой сильно смещенное нормальное распределение. Слева от пика нет никакого хвоста (посетитель явно не может быть на веб-сайте менее 0 сек.). Сначала данные круто убывают вправо и потом тянутся вдоль оси X намного дольше, чем можно было бы ожидать от данных, которые нормально распределены.
Когда встречаются подобные распределения, где большинство значений малы, и иногда случаются предельные значения, может оказаться полезным изобразить ось Y в виде логарифмической шкалы. Логарифмические шкалы используются для того, чтобы представлять события, которые меняются в очень широких пределах. Оси графика обычно линейны, и они делят диапазон на равноразмерные шаги подобно «числовой оси», которую мы изучали в школе. В отличие от них, логарифмические шкалы делят диапазон на шаги, которые становятся все длиннее и длиннее по мере удаления от источника.
Некоторые системы измерения природных явлений, которые изменяются в очень широких пределах, представлены в логарифмической шкале. Например, шкала Рихтера для измерения интенсивности землетрясений является логарифмической шкалой по основанию 10, что означает, что землетрясение магнитудой 5 баллов по шкале Рихтера в 10 раз интенсивнее землетрясения магнитудой 4 балла. Децибельная шкала громкости тоже имеет логарифмическую шкалу, но с другим основанием — звуковая волна магнитудой 30 децибелов в 10 раз больше звуковой волны в 20 децибелов. В каждом случае принцип один и тот же — использование логарифмической шкалы позволяет сжать очень широкий предел значений в диапазон гораздо меньшего размера.
Изобразить на графике ось Y с логарифмической шкалой достаточно легко при помощи именованного аргумента logy=True функции pandas plot.hist:
def ex_2_3():
load_data('dwell-times.tsv')['dwell-time'].plot.hist(bins=20, logy=True)
plt.xlabel('Время пребывания, сек.')
plt.ylabel('Логарифмическая частота')
plt.show() В библиотеке pandas по умолчанию используется десятичная логарифмическая шкала, каждое деление на оси которой представляет собой интервал в 10 раз шире относительно предыдущего. График, в котором только одна ось имеет логарифмическую шкалу, называется полулогарифмическим или лог-линейным. Неудивительно, что график с двумя логарифмическими осями называется просто логарифмическим или логлог-линейным графиком (иногда также двойным логарифмическим, loglog=True).

Нанесение данных времени пребывания на полулогарифмический график показывает, что они обладают скрытой связностью — имеется линейная связь между временем пребывания и логарифмом частоты. На графике ясность связи ухудшается справа, где число посетителей меньше 10, но, помимо этого, связь удивительно постоянная.
Прямая линия на полулогарифмическом графике — это явный индикатор экспоненциального распределения.
Экспоненциальное распределение
Экспоненциальное (или показательное) распределение часто встречается в ситуациях, когда имеется много малых положительных значений и намного меньше более крупных. С учетом того, что мы узнали о шкале Рихтера, не будет никаким секретом, что магнитуда землетрясений подчинена экспоненциальному распределению.
Кроме того, это распределение часто встречается в период ожидания — время до наступления следующего землетрясения любой магнитуды тоже приближенно подчиняется экспоненциальному распределению. Это распределение часто используется для имитационного моделирования интенсивности отказов, которые по существу являются временем ожидания события, когда механизм выйдет из строя. Наше экспоненциальное распределение моделирует процесс, аналогичный поломке — время ожидания события, когда посетитель заскучает и покинет веб-сайт.
Экспоненциальное распределение характерно многими интересными свойствами. Одно из них имеет отношение к среднему значению и стандартному отклонению:
def ex_2_4():
ts = load_data('dwell-times.tsv')['dwell-time']
print('Среднее: ', ts.mean())
print('Медиана: ', ts.median())
print('Стандартное отклонение:', ts.std())Среднее: 93.2014074074074
Медиана: 64.0
Стандартное отклонение: 93.96972402519819Среднее значение и стандартное отклонение очень похожи. Фактически, для идеального экспоненциального распределения они абсолютно одинаковые. Это свойство сохраняется для всех экспоненциальных распределений — при увеличении средних увеличиваются и стандартные отклонения.
Для экспоненциальных распределений средние значения и стандартные отклонения эквивалентны.
Вторым свойством экспоненциального распределения является отсутствие памяти (или последействия). Это противоречащее интуитивному пониманию свойство лучше всего проиллюстрировать на примере. Мы ожидаем, что пока посетитель продолжает просматривать наш веб-сайт, вероятность, что ему надоест, и он покинет веб-сайт, увеличивается. Поскольку среднее время пребывания составляет 93 сек., то может создаться впечатление, что за пределами этих 93 сек., он будет продолжать просмотр веб-сайта все в меньшей степени.
Свойство отсутствия памяти экспоненциальных распределений говорит о том, что вероятность, что посетитель останется на нашем веб-сайте в течение следующих 93 сек. совершенно одинаковая, независимо от того, находится он на веб-сайте уже 93 сек., 5 мин. или целый час, либо только что на него зашел.
Для распределения без памяти количество истекшего времени не влияет на вероятность продолжения события в течение дополнительных x минут.
Свойство отсутствия памяти экспоненциальных распределений частично объясняет причину, почему очень трудно предсказывать время следующего землетрясения. Нам приходится опираться не на истекшее время, а на другие подтверждающие данные (такие как отклонения в геомагнетизме).
Поскольку медианное время пребывания составляет 64 сек., то примерно половина наших посетителей остаются на веб-сайте в течение примерно всего одной минуты. Среднее значение в 93 сек. показывает, что некоторые посетители остаются намного дольше медианы. Эти статистики были вычислены по всем посетителям за последние 6 месяцев. Было бы интересно узнать, каким образом эти статистики варьируются в расчете на один день. Давайте их вычислим.
Распределение среднесуточных значений
Предоставленный веб-командой файл включает метку даты посещения. В целях агрегирования данных по дням, необходимо удалить ту часть метки даты, которая соответствует времени. Хотя мы можем проделать это при помощи нативных средств Python, более гибкий подход состоит в использовании функционала pandas для обработки даты и времени — функции to_datetime.
На входе она принимает строковое значение, значение с типом date-time, список, кортеж, 1-мерный массив либо числовой ряд Series библиотеки pandas как в нашем случае, а также набор именованных аргументов. Например, именованный аргумент errors='ignore' позволяет проигнорировать даты, которые неправильно отформатированы либо выходят за допустимые пределы. Отметим также, что в функции mean_dwell_times_by_date использован вспомогательный метод resample для частотных преобразований и перестановки временного ряда. Он выполняет группировку по дате-времени, а после него следует метод свертки по каждой группе. В данном случае аргумент 'D' группирует по будним дням, и затем каждая группа агрегируется методом mean. Таким образом, выражение dt.resample('D').mean() берет средние значения по будним дням:
def with_parsed_date(df):
'''Привести поле date к типу date-time'''
df['date'] = pd.to_datetime(df['date'], errors='ignore')
return df
def filter_weekdays(df):
'''Отфильтровать по будним дням'''
return df[df['date'].index.dayofweek < 5] # понедельник..пятница
def mean_dwell_times_by_date(df):
'''Среднесуточные времена пребывания'''
df.index = with_parsed_date(df)['date']
return df.resample('D').mean() # перегруппировать
def daily_mean_dwell_times(df):
'''Средние времена пребывания с фильтрацией - только по будним дням'''
df.index = with_parsed_date(df)['date']
df = filter_weekdays(df)
return df.resample('D').mean()Сочетание приведенных выше функций позволяет вычислить среднее, медиану и стандартное отклонение для времен пребывания по будним дням:
def ex_2_5():
df = load_data('dwell-times.tsv')
mus = daily_mean_dwell_times(df)
print('Среднее: ', float(means.mean()))
print('Медиана: ', float(means.median()))
print('Стандартное отклонение: ', float(means.std()))Среднее: 90.21042865056198
Медиана: 90.13661202185793
Стандартное отклонение: 3.7223429053200348По будним дням среднее значение составляет 90.2 сек. Оно близко к среднему значению, которое мы вычислили ранее по всему набору данных, включая выходные дни. А вот стандартное отклонение намного ниже, всего 3.7 сек. Другими словами, распределение значений по будним дням имеет стандартные отклонения намного ниже, чем по всему набору данных. Давайте построим гистограмму значений времен пребывания по будним дням:
def ex_2_6():
df = load_data('dwell-times.tsv')
daily_mean_dwell_times(df)['dwell-time'].hist(bins=20)
plt.xlabel('Время пребывания по будним дням, сек.')
plt.ylabel('Частота')
plt.show()Этот пример сгенерирует следующую ниже гистограмму:
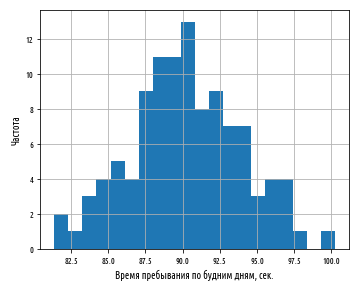
Распределение средних значений в выборках расположено симметрично вокруг общего популяционного среднего значения, равного 90 сек. со стандартным отклонением 3.7 сек. В отличие от распределения, из которого эти средние были отобраны, т.е. экспоненциального распределения, распределение выборочных средних нормально распределено.
Центральная предельная теорема
Мы встречались с центральной предельной теоремой в предыдущей серии постов, когда делали выборки из равномерного распределения и их усредняли. На самом деле, центральная предельная теорема работает для любого распределения значений при условии, что это распределение имеет конечное стандартное отклонение.
Согласно центральной предельной теореме, распределение выборочных средних нормально распределено независимо от распределения, из которого они были вычислены.
То, что опорное распределение - экспоненциальное, не играет никакой роли — центральная предельная теорема показывает, что средние значения случайных выборок, взятых из любого распределения, близко аппроксимируют нормальное распределение. Теперь давайте построим график нормальной кривой поверх нашей гистограммы, чтобы посмотреть, насколько близко она совпадает.
В целях выведения нормальной кривой поверх гистограммы последняя должна быть построена как гистограмма плотностей распределения. Она изображает не частоту, а долю всех точек, помещенных в каждую корзину. После чего мы сможем наложить нормальную плотность вероятности с тем же средним значением и стандартным отклонением (Обратите внимание на применение функции dropna, которая удаляет строки, где есть пропущенные значения):
def ex_2_7():
'''Подгонка нормальной кривой поверх гистограммы'''
df = load_data('dwell-times.tsv')
means = daily_mean_dwell_times(df)['dwell-time'].dropna()
ax = means.hist(bins=20, density=True)
xs = sorted(means) # корзины
df = pd.DataFrame()
df[0] = xs
df[1] = stats.norm.pdf(xs, means.mean(), means.std())
df.plot(0, 1, linewidth=2, color='r', legend=None, ax=ax)
plt.xlabel('Время пребывания по будним дням, сек.')
plt.ylabel('Плотность')
plt.show()Этот пример сгенерирует следующий ниже график:

Нормальная кривая, изображенная поверх гистограммы, имеет стандартное отклонение, равное примерно 3.7 сек. Другими словами, она количественно определяет изменчивость каждого значения в будние дни относительно общего среднего значения, равного 90 сек. Можно представить среднее каждого дня как выборку из общей популяции, где изображенная выше кривая показывает распределение средних по выборкам. Поскольку 3.7 сек. — это величина, на которую среднее значение выборки отличается от популяционного среднего, она называется стандартной ошибкой.
Стандартная ошибка
В то время как стандартное отклонение измеряет величину изменчивости внутри выборки, стандартная ошибка (Standard Error, аббр. SE) среднего, измеряет величину изменчивости между средними значениями выборок, взятыми из той же самой популяции.
Стандартная ошибка среднего — это стандартное отклонение распределения средних по выборкам.
Мы вычислили стандартную ошибку времени пребывания эмпирически, глядя на данные за предыдущие 6 месяцев. Однако существует уравнение, которое позволяет ее вычислять, исходя из одной единственной выборки:
Здесь σx — это стандартное отклонение, подсчитанное по выборке x, и n — размер выборки. Эта формула не похожа на описательные статистики, которые мы встречали в предыдущей серии постов. Они описывали одиночную выборку. В отличие от них, стандартная ошибка пытается описать свойство выборок в целом — величину изменчивости в средних значениях выборок, которую можно ожидать для выборок заданного размера:
def variance(xs):
'''Несмещенная дисперсия (варианс) при n <= 30'''
x_hat = xs.mean()
n = len(xs)
n = n-1 if n in range(1, 30) else n
square_deviation = lambda x : (x – x_hat) ** 2
return sum( map(square_deviation, xs) ) / n
def standard_deviation(xs):
return sp.sqrt(variance(xs))
def standard_error(xs):
return standard_deviation(xs) / sp.sqrt(len(xs))Стандартная ошибка среднего таким образом связана с двумя факторами:
Размером выборки
Популяционным стандартным отклонением
Размер выборки оказывает самое большое влияние на стандартную ошибку. Для того, чтобы уменьшить размер стандартной ошибки вдвое, мы должны увеличить его в четыре раза, поскольку мы берем квадратный корень размера выборки.
Может показаться странным, что доля популяции, из которой отбирается выборка, никак не влияет на размер стандартной ошибки. Но это именно так, поскольку некоторые популяции могут иметь бесконечные размеры.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
Темой следующего поста, поста №2, будет разница между выборками и популяцией, а также интервал уверенности. Да-да, именно интервал уверенности, а не доверительный интервал.
