Во вчерашней статье про «задачу Танежи или проблемы числа 10958», я попытался представить конкатенацию чисел как алгебраическую операцию. И пока делал расчеты, понял, что мы можем переводить числа меду система счисления только на основе их умножения.
Для начала, еще раз, распишем, что такое «Алгебраическая конкатенация».
Для примера возьмем число 10958 и представим его с операцией конкатенации, а именно: 1‖0‖9‖5‖8 = (((1 * 10 + 0) * 10 + 9) * 10 + 5) * 10 + 8.
Т.е операция «конкатенации» это: a ‖ b = (a * 10) + b; Но 10 — это «хитрое» число… Это число следующие за максимальным в системе счисления, ну т.е. это просто основание системы счисления т.е. общий вид такой:
a ‖ b = (a * m) + b, где m – основание системы счисления представленное в обозначении самой системы.
Но такое определение мне не очень нравится, ибо m больше чем возможные числа внутри системы. Давайте сделаем чуть хитрее.
a ‖ b = (a * 10) + b – легче для восприятия.
Давайте, на всякий случай, проверим, что действительно это работает и пересчитаем описанные выше операции на 10958.
Двоичная: 10 1010 1100 1110 = 1‖0‖1‖0‖1‖0‖1‖1‖0‖0‖1‖1‖1‖0 = ((((((((((((1 * 10 + 0) * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 1) * 10 + 0) * 10 + 0) * 10 + 1) * 10 + 1) * 10 + 1) * 10 + 0
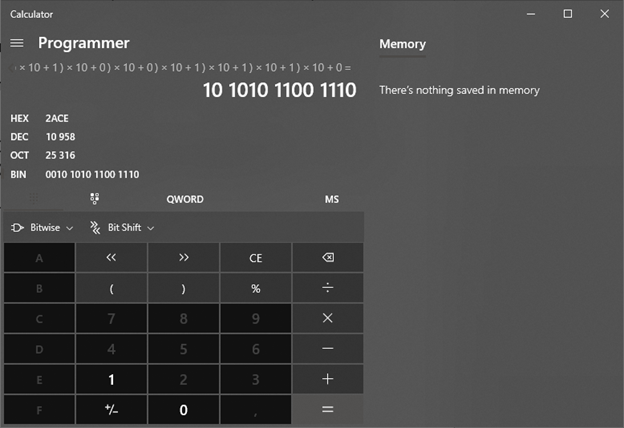
Восьмеричная: 25316 = 2‖5‖3‖1‖6 = (((2 * 10 + 5) * 10 + 3) * 10 + 1) * 10 + 6
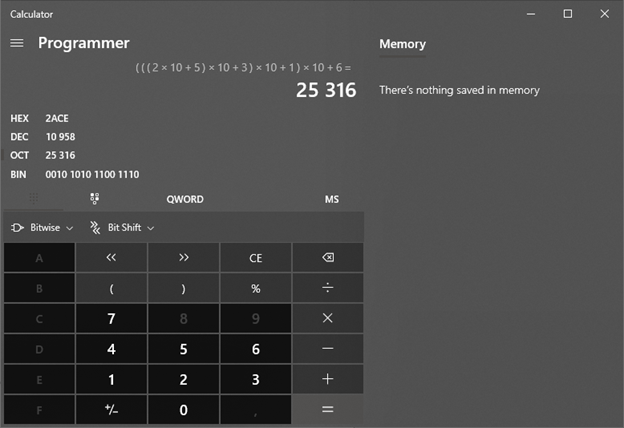
Шестнадцатеричная 2ACE = 2‖A‖C‖E = ((2 * 10 + A) * 10 + C) * 10 + E
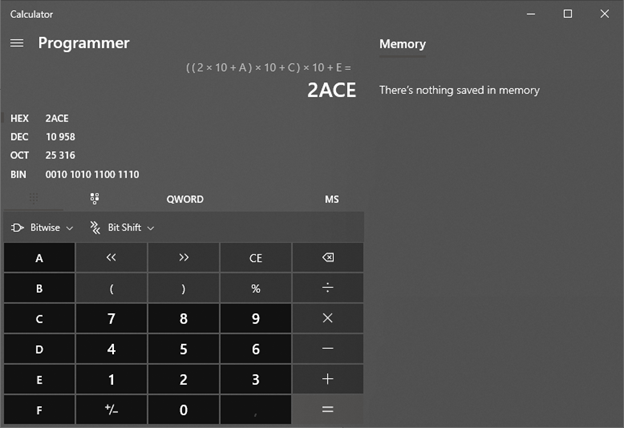
И тут кроется собственно фокус быстрого перевода чисел из одно системы счисления в другую.
Причем на ней сохраняются свойства обычной конкатенации:
1) Операция конкатенации неассоциативна.
То есть, если нужно выполнить конкатенацию трёх цифр, то от расстановки скобок результат изменится: ( 1 ‖ 2) ‖ 3 = 123, и в то же время 1 ‖ ( 2 ‖ 3 ) = 33.
2) Операция конкатенации некоммутативна.
В самом деле, wiki ‖ media = wikimedia, но media ‖ wiki = mediawiki ≠ wikimedia. От перестановки операндов меняется результат операции, что и означает её некоммутативность.
3) Пустое слово — ε, — является нейтральным элементом (единицей) операции конкатенации.
То есть, если ε— пустое слово, то для любого слова α выполнено равенство: ε ‖ a = a ‖ ε = a
4) Длина (количество букв) конкатенации слов равна сумме длин операндов:
|α ‖ β| = |α| + |β|.
Но для начала рассмотрим классический способ перевода чисел из десятичной системы в восьмеричную. Для это используется операция деления и взятие остатка от деления.
Для примера возьмем 672 и переведем его восьмеричную систему счисления.
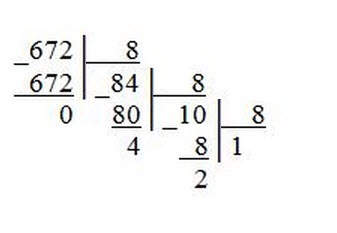
А перевод числа 934 в шестнадцатеричную систему счисления выглядит так.

Количество тактов по расчету чисел здесь довольно больше.
Более того перевод целого числа в систему счисления с новым основанием всегда делается через десятичную систему счисления. Т.е. число из исходной системы счисления загоняем в десятичное, а потом это число из десятичное систему счисления переводим в финальную систему счисления.
Как-то очень муторно…
Есть конечно таблицы триад и тетрад. Которые позволяют переводить числа из двоичной системы счисления в восьмеричную и шестнадцатеричную. Но это всё.
Вчера удалось понять, что операция «алгебраической конкатенации» позволяет нам упростить перевод до базового умножения. И переводить из любой системы счислению в любую другую без промежуточного звена, но нам потребуется пара таблиц-представлений.
Таблица 1 – представление цифр в разных системах счисления:

По горизонтали мы видим здесь представление числа в разных система счисления, а по вертикали указана основание системы счисления.
Далее распишем как выглядят основания одной системы счисления в другой системе счисления. Т.е. размерность системы в представлении другой системы. Например, основание десятичной системы счисления в шестнадцатеричной выглядит так:
Таблица 2 – множители основания системы в разных система ��числения.

По горизонтали здесь исходная система счисления, а по вертикали – та, в которую хотим перевести.
Получается, чтобы перевести число 934 из десятичной системы счисления в шестнадцатеричную мы просто берем числа из таблицы.
9‖3‖4
= (9 * 10 + 3) * 10 + 4 — запись в десятичной системе
= (9 * A + 3) * A + 4 — здесь и далее уже шестнадцатеричная система
= (5A + 3) * A + 4
= 5D * A + 4
= 3A2 + 4
= 3A6
Возьмем еще одно число, на этот раз в двоичной системе счисления 1101011, и попробуем получить восьмеричную, потом десятичную и обратно в двоичную
1101011
= 1‖1‖0‖1‖0‖1‖1 — запись в двоичной системе
= (((((1 * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 1 — запись в двоичной системе
= (((((1 * 2 + 1) * 2 + 0) * 2 + 1) * 2 + 0) * 2 + 1) * 2 + 1 — восьмеричная система
= 153 — восьмеричная система
= 1‖5‖3
= (1 * 10 + 5) * 10 + 3 — восьмеричная система
= (1 * 8 + 5) * 8 + 3 – в десятичной системе
= 107 – в десятичной системе
= 1‖0‖7 – в десятичной системе
= (1 * 10 + 0) * 10 + 7 – в десятичной системе
= (1 * 1010 + 0) * 1010 + 111- запись в двоичной системе
= 1101011 — запись в двоичной системе.
Собственно, этим можно заниматься весь день.
Важное замечание. В наших расчетах есть две строчки:
…
= (((((1 * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 1 — запись в двоичной системе
= (((((1 * 2 + 1) * 2 + 0) * 2 + 1) * 2 + 0) * 2 + 1) * 2 + 1 — восьмеричная система
…
Вторая строка, (((((1 * 2 + 1) * 2 + 0) * 2 + 1) * 2 + 0) * 2 + 1) * 2 + 1 будет выглядеть абсолютно точно также и в 3-х, 4-х, … 8-ми, 16-ти и.д. -значной системе счисления.
Тут нужно понимать, что операции, которые мы выполним над это строкой уже делаются в указанной системе счисления, поэтому и результат будет отличаться.
По сути мы получили универсальную систему перевода целых чисел. В которой не нужно ни деление и взятие остатков. И даже перевода во вспомогательную систему счисления.
Но нужно будет подумать над дробной частью, что-то сходу она мне не поддалась…
P.S.
Я поискал в сети способы перевода одной системы в другую, но что-то везде всё упирается во взятие остатков, а прямого перевода через умножение я так и не нашел. Может плохо искал?
Ведь по факту, с точки зрения визуального представление, — это просто смещение числа по разрядам и всё… Странно как-то, что нет описания такого просто решения… Ибо больше напоминает математический фокус, чем что-то новое и необычное. В чем я не прав? Жду ваших замечаний.
Алгебраическая конкатенация
Для начала, еще раз, распишем, что такое «Алгебраическая конкатенация».
Для примера возьмем число 10958 и представим его с операцией конкатенации, а именно: 1‖0‖9‖5‖8 = (((1 * 10 + 0) * 10 + 9) * 10 + 5) * 10 + 8.
Т.е операция «конкатенации» это: a ‖ b = (a * 10) + b; Но 10 — это «хитрое» число… Это число следующие за максимальным в системе счисления, ну т.е. это просто основание системы счисления т.е. общий вид такой:
a ‖ b = (a * m) + b, где m – основание системы счисления представленное в обозначении самой системы.
Но такое определение мне не очень нравится, ибо m больше чем возможные числа внутри системы. Давайте сделаем чуть хитрее.
a ‖ b = (a * 10) + b – легче для восприятия.
Давайте, на всякий случай, проверим, что действительно это работает и пересчитаем описанные выше операции на 10958.
Двоичная: 10 1010 1100 1110 = 1‖0‖1‖0‖1‖0‖1‖1‖0‖0‖1‖1‖1‖0 = ((((((((((((1 * 10 + 0) * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 1) * 10 + 0) * 10 + 0) * 10 + 1) * 10 + 1) * 10 + 1) * 10 + 0

Восьмеричная: 25316 = 2‖5‖3‖1‖6 = (((2 * 10 + 5) * 10 + 3) * 10 + 1) * 10 + 6

Шестнадцатеричная 2ACE = 2‖A‖C‖E = ((2 * 10 + A) * 10 + C) * 10 + E

И тут кроется собственно фокус быстрого перевода чисел из одно системы счисления в другую.
Причем на ней сохраняются свойства обычной конкатенации:
1) Операция конкатенации неассоциативна.
То есть, если нужно выполнить конкатенацию трёх цифр, то от расстановки скобок результат изменится: ( 1 ‖ 2) ‖ 3 = 123, и в то же время 1 ‖ ( 2 ‖ 3 ) = 33.
2) Операция конкатенации некоммутативна.
В самом деле, wiki ‖ media = wikimedia, но media ‖ wiki = mediawiki ≠ wikimedia. От перестановки операндов меняется результат операции, что и означает её некоммутативность.
3) Пустое слово — ε, — является нейтральным элементом (единицей) операции конкатенации.
То есть, если ε— пустое слово, то для любого слова α выполнено равенство: ε ‖ a = a ‖ ε = a
4) Длина (количество букв) конкатенации слов равна сумме длин операндов:
|α ‖ β| = |α| + |β|.
Классический способ смены системы счисления
Но для начала рассмотрим классический способ перевода чисел из десятичной системы в восьмеричную. Для это используется операция деления и взятие остатка от деления.
Для примера возьмем 672 и переведем его восьмеричную систему счисления.

А перевод числа 934 в шестнадцатеричную систему счисления выглядит так.

Количество тактов по расчету чисел здесь довольно больше.
Более того перевод целого числа в систему счисления с новым основанием всегда делается через десятичную систему счисления. Т.е. число из исходной системы счисления загоняем в десятичное, а потом это число из десятичное систему счисления переводим в финальную систему счисления.
Как-то очень муторно…
Есть конечно таблицы триад и тетрад. Которые позволяют переводить числа из двоичной системы счисления в восьмеричную и шестнадцатеричную. Но это всё.
Смена системы счисления через алгебраическую конкатенацию
Вчера удалось понять, что операция «алгебраической конкатенации» позволяет нам упростить перевод до базового умножения. И переводить из любой системы счислению в любую другую без промежуточного звена, но нам потребуется пара таблиц-представлений.
Таблица 1 – представление цифр в разных системах счисления:

По горизонтали мы видим здесь представление числа в разных система счисления, а по вертикали указана основание системы счисления.
Далее распишем как выглядят основания одной системы счисления в другой системе счисления. Т.е. размерность системы в представлении другой системы. Например, основание десятичной системы счисления в шестнадцатеричной выглядит так:
Таблица 2 – множители основания системы в разных система ��числения.

По горизонтали здесь исходная система счисления, а по вертикали – та, в которую хотим перевести.
Получается, чтобы перевести число 934 из десятичной системы счисления в шестнадцатеричную мы просто берем числа из таблицы.
9‖3‖4
= (9 * 10 + 3) * 10 + 4 — запись в десятичной системе
= (9 * A + 3) * A + 4 — здесь и далее уже шестнадцатеричная система
= (5A + 3) * A + 4
= 5D * A + 4
= 3A2 + 4
= 3A6
Возьмем еще одно число, на этот раз в двоичной системе счисления 1101011, и попробуем получить восьмеричную, потом десятичную и обратно в двоичную
1101011
= 1‖1‖0‖1‖0‖1‖1 — запись в двоичной системе
= (((((1 * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 1 — запись в двоичной системе
= (((((1 * 2 + 1) * 2 + 0) * 2 + 1) * 2 + 0) * 2 + 1) * 2 + 1 — восьмеричная система
= 153 — восьмеричная система
= 1‖5‖3
= (1 * 10 + 5) * 10 + 3 — восьмеричная система
= (1 * 8 + 5) * 8 + 3 – в десятичной системе
= 107 – в десятичной системе
= 1‖0‖7 – в десятичной системе
= (1 * 10 + 0) * 10 + 7 – в десятичной системе
= (1 * 1010 + 0) * 1010 + 111- запись в двоичной системе
= 1101011 — запись в двоичной системе.
Собственно, этим можно заниматься весь день.
Важное замечание. В наших расчетах есть две строчки:
…
= (((((1 * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 0) * 10 + 1) * 10 + 1 — запись в двоичной системе
= (((((1 * 2 + 1) * 2 + 0) * 2 + 1) * 2 + 0) * 2 + 1) * 2 + 1 — восьмеричная система
…
Вторая строка, (((((1 * 2 + 1) * 2 + 0) * 2 + 1) * 2 + 0) * 2 + 1) * 2 + 1 будет выглядеть абсолютно точно также и в 3-х, 4-х, … 8-ми, 16-ти и.д. -значной системе счисления.
Тут нужно понимать, что операции, которые мы выполним над это строкой уже делаются в указанной системе счисления, поэтому и результат будет отличаться.
Вывод
По сути мы получили универсальную систему перевода целых чисел. В которой не нужно ни деление и взятие остатков. И даже перевода во вспомогательную систему счисления.
Но нужно будет подумать над дробной частью, что-то сходу она мне не поддалась…
P.S.
Я поискал в сети способы перевода одной системы в другую, но что-то везде всё упирается во взятие остатков, а прямого перевода через умножение я так и не нашел. Может плохо искал?
Ведь по факту, с точки зрения визуального представление, — это просто смещение числа по разрядам и всё… Странно как-то, что нет описания такого просто решения… Ибо больше напоминает математический фокус, чем что-то новое и необычное. В чем я не прав? Жду ваших замечаний.
