Настал тот редкий случай, когда в работе программиста микроконтроллеров появилась потребность в математике и даже физике. У меня на работе была интересная задача по теме разработки тяжелой (70кг) PTZ камеры.

Там была задачка по физике из раздела кинематики. Правда по уровню сложности её можно отнести к школьной программе 6го класса.
Шаговые двигатели применяются в CNC станках, 2D/3D принтерах, жестких дисках, сканерах, плоттерах, PTZ камерах, крутилках радарных антенн, турелей, в линейных актюаторах, в стрелочных приборах (аналоговые часы) и может быть еще где-то.
У шаговых двигателей есть одна проблема. Из-за высоких моментов инерции нагрузки шаговые двигатели могут потерять шаги и не отработать команды. Чтобы минимизировать потерю шагов вал шагового двигателя надо раскручивать плавно. Самый простой способ - это использовать трапециевидные профили движения.
Постановка задачи
дано:
Параметр | Пояснение | Units |
PhiSet | Угол на который надо повернуть вал шагового двигателя | Radians |
OmegaMax | Максимально возможная угловая частота | Radians/s |
BettaMax | Максимальное угловое ускорение | Radians/(s^2) |
Дан угол, PhiSet на который следует повернуть вал шагового двигателя. Двигатель работает в трех режимах: ускорение ACCEL, работа на постоянной крейсерской скорости RUN, замедление DECEL. Получается трапециевидный профиль скорости.
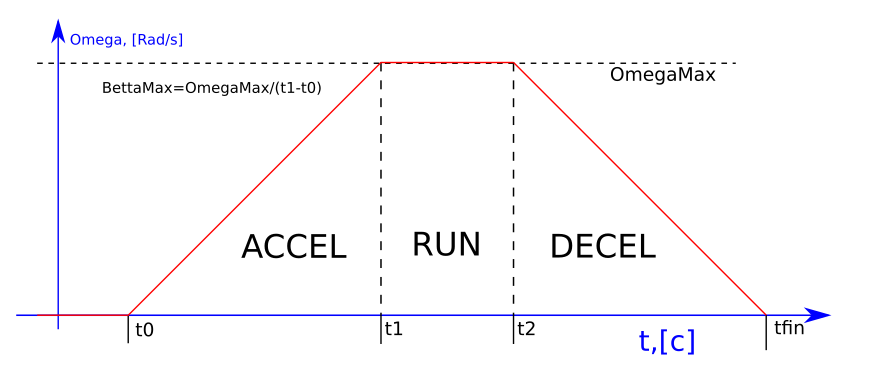
Или ускорение ACCEL и замедление DECEL. Получается треугольный профиль скорости (в случае, если крейсерская скорость OmegaMax очень высока, а угловой путь PhiSet, что надо пройти, очень мал).
В качестве параметров движения даны только ускорение BettaMax [rad/s^2] и крейсерская скорость OmegaMax [rad/s] в режиме RUN. В нулевой момент времени t0 вал трогается с места и начинает набирать угловую скорость Omega с постоянным ускорением BettaMax. Вычислить момент времени t1, при котором следует остановить ускорение ACCEL и начать вращение на постоянной скорости OmegaMax (фаза RUN), и вычислить момент время t2, при котором следует остановить движение на постоянной скорости OmegaMax RUN и начать замедление DECEL.
Примечание
Моменты времени t1 и t2 могут совпадать, если BettaMax очень высоко, а PhiSet мало. Для симметрии и простоты положим, что ускорение во время набора скорости и ускорение во время замедления по модулю равны BettaMax, но противоположны по знаку.
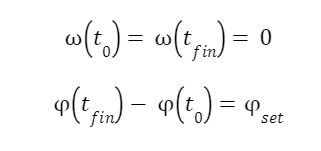
Терминология
Профиль - это график зависимости угловой скорости от времени Omega(t).
Фаза RUN - движение с постоянной скоростью.
Хороший инженер должен не только решить задачу, но и быть способным внятно объяснить доступным языком свое решение коллегам.
Решение
Из кинематики известно, что путь это интеграл скорости по времени. В данном случае интеграл считать нет смысла так как фигуры простецкие: 2 треугольника да прямоугольник.
Первым делом процессор должен решить нужна ли вообще фаза RUN?
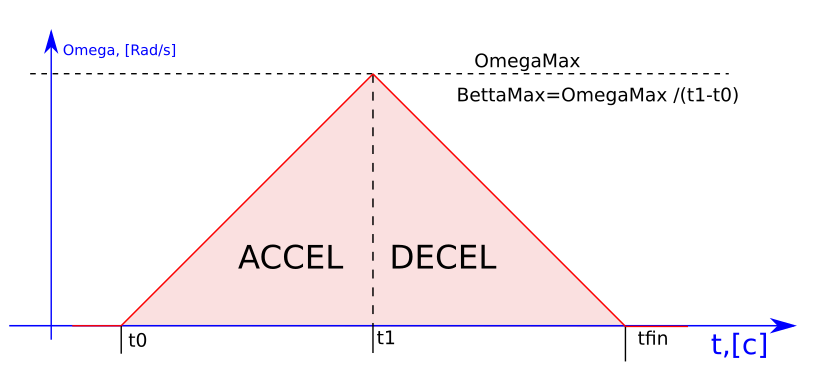
Площадь равнобедренного треугольника равна S0. По сути можно сложить квадрат.
Если phi_set < S0, то фаза RUN не нужна и получится треугольный профиль. Если S0 < phi_set, то фаза RUN однозначно нужна и получится трапецевидный профиль. Как выразить S0 зная BettaMax?
Получается что S0
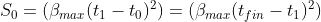
При треугольном профиле получается, что
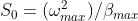
Треугольный профиль (phi_set <= S0)
Ок. Как же определить t1(время переключения) в случае треугольного профиля? Надо просто решить данную систему уравнений. Выразить t1. t0 можно обнулить.


Выразив OmegaTop из каждой формулы и приравняв их можно выразить t1. Получается
А теперь случай трапецевидного профиля (S0 < phi_set)
С t1 просто. Из OmegaMax=BettaMax*t1 получаем
В трапецевидном профиле площадь состоит из 2х треугольников и одного прямоугольника
ввиду симметрии получим
Выражаем время включения фазы замедления
Как видите все расчеты был составлен чисто из геометрических соображений (площадь графика ω(t) всегда должна быть равна phi_set ).
Ниже представлен простой алгоритм на языке ДРАКОН, который помогает наглядно показать алгоритм вычисления моментов времени t1 и t2 переключения режимов ACCEL/RUN/DECEL при повороте на угол set в условиях заданной скорости OmegaMax в режиме RUN и допустимого ускорения BettaMax.
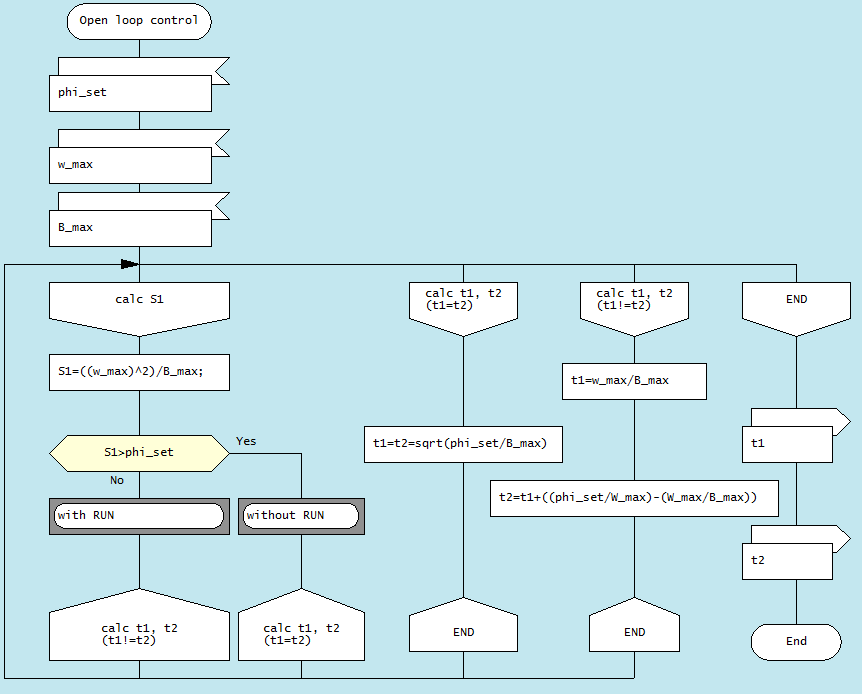
Решение на языке MATLAB
function [ t1 t2 tf wlim] = calcTimesF( phi_set, w_max, B_max ) S1=((w_max)^2)/B_max; if(phi_set < S1) %without RUN t1= t2 t1=sqrt(phi_set/B_max); t2=t1; tf=2*t1; wlim = B_max*t1; else %with RUN t1 < t2 t1=w_max/B_max; t2=(phi_set/w_max); tf=t2+t1; wlim = w_max; end end
Эту задачу в реальности надо решать для дискретного движения, так как в реальности имеем дело с шаговым двигателем. Там заметно усложняется решение. В изменении стадии движения (ACCEL, RUN, DECEL ) приходится ориентироваться не по времени, как в непрерывной постановке, а по пройденному пути (количеству сделанных шагов шагового двигателя). Так как MCU(шка) отлично считает количество положительных фронтов на проводе STEP. Плюс нужна реализация функции квадратного корня на уровне прошивки. Про это есть публикация Asynchronous Control System for Stepper Motor With an Incremental Encoder Feedback.
Вывод
Как видите обыкновенной школьной математики вполне достаточно, чтобы решать реальные оценочные задачи из prod(a) станкостроения.
При расчетах всегда на каждом шаге проверяйте размерность в формулах.
Если вы программируете микроконтроллеры и вам приходилось прибегать к математике, то пишите это в комментариях.
Акроним | расшифровка |
PTZ | Pan-tilt-zoom |
CNC | computer numerical control |
Links
Online редактор формул http://latex.codecogs.com/eqneditor/editor.php
