nrsharip 18 мар в 17:32

Основные типы распределений вероятностей в примерах

Средний

15 мин

32K

Python*Алгоритмы*Математика*Статистика в ITИнфографика

Статистические исследования и эксперименты являются краеугольным камнем развития любой компании. Особенно это касается интернет-проектов, где учёт количества пользователей в день, времени нахождения на сайте, нажатий на целевые кнопки, покупок товаров является обычным и необходимым явлением. Любые изменения в пользовательском опыте на сайте компании (внешний вид, структура, контент) приводят к изменениям в работе пользователя и, как результат, изменения наблюдаются в собираемых данных. Важным элементом анализа изменений данных и его фундаментом является использование основных типов распределений случайных величин, от понимания которых напрямую зависит качество оценки значимости наблюдаемого изменения.

В данной статье я сделаю упор не на функции и формулы, которые обычно сопутствуют распределениям (функции вероятности, распределения, PMF, PDF, CDF) - их можно легко найти самостоятельно. Скорее я попытаюсь показать как генерируются те или иные распределения на конкретных примерах. Это, на мой взгляд, нагляднее и важнее для понимания сути этих распределений и того, как они в итоге применяются на практике для решения конкретных задач анализа. Хотел бы обратить внимание на статью "Как сравнивать распределения. От визуализации до статистических тестов", т. к. это пример основной работы с распределениями - их сравнение на предмет статистической значимости произошедших изменений с помощью статистических тестов. Также, в качестве углубленного материала, рекомендую интересный метод работы с отдельной выборкой без использования статистических тестов, который описан в статье "Бутстрап в A/B-тестах: швейцарский нож аналитика"

Примечание: в данной публикации намеренно минимизируется использование уже готовых функций генерации случайных величин из определённых распределений (например, scipy.stats.norm.rvs())

Список распределений вероятностей

Биномиальное распределение
Распределение Пуассона
Экспоненциальное распределение
Распределение Вейбулла
Гамма-распределение
Бета-распределение
Гипергеометрическое распределение
Нормальное распределение
Распределение Стьюдента (t-распределение)
Распределение Хи-квадрат
Распределение Фишера

1. Биномиальное распределение

Схема формирования выборок и получения искомых величин: заполняем 1000 массивов размером единицами с вероятностью , остальные позиции заполняем нулями. Количества единиц (успехов) в каждом массиве являются искомыми случайными величинами, формирующими Биноминальное распределение.

Основная часть программы для получения выборок и искомых величин (полный код программы):

X_RANGE = 1000
Y_RANGE = 20
P_1 = 0.1 # вероятность успеха для первого распределения
P_2 = 0.5 # вероятность успеха для второго распределения
P_3 = 0.8 # вероятность успеха для третьего распределения
...
for i in range(X_RANGE): 
    sample1 = [1 if r < P_1 else 0 for r in [random.random() for i in range(Y_RANGE)]]
    sample2 = [1 if r < P_2 else 0 for r in [random.random() for i in range(Y_RANGE)]]
    sample3 = [1 if r < P_3 else 0 for r in [random.random() for i in range(Y_RANGE)]]

    distr1.loc[i] = sample1.count(1)
    distr2.loc[i] = sample2.count(1)
    distr3.loc[i] = sample3.count(1)
    ...

Результат работы:

(к оглавлению)

2. Распределение Пуассона

Схема формирования выборок и получения искомых величин: заполняем 1000 массивов размером единицами с вероятностью , остальные позиции заполняем нулями. берём достаточно большим, а среднее количество единиц (успехов) $\lambda=n \times p$ . Количества единиц (успехов) в каждом массиве являются искомыми случайными величинами, формирующими распределение Пуассона.

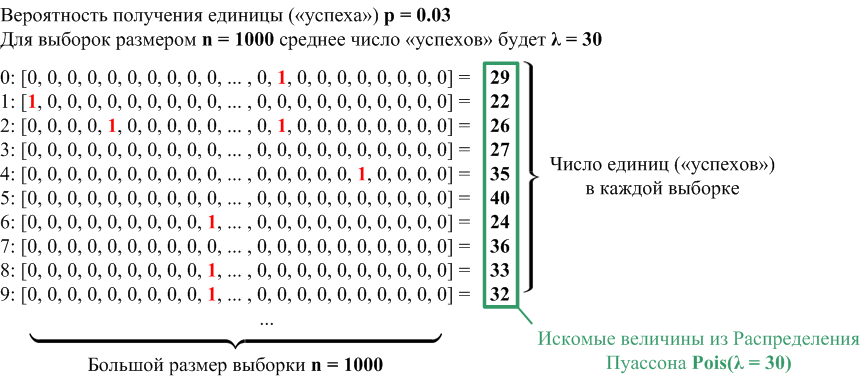
Основная часть программы для получения выборок и искомых величин (полный код программы):

X_RANGE = 1000 # 1000 выборок
Y_RANGE = 1000 # размер одной выборки достаточно большой
P1 = 0.001 # вероятность успеха для первого распределения (среднее успехов для 1000 экспериментов λ = 1)
P2 = 0.01 # вероятность успеха для второго распределения (среднее успехов для 1000 экспериментов λ = 10)
P3 = 0.03 # вероятность успеха для третьего распределения (среднее успехов для 1000 экспериментов λ = 30)
...
for i in range(X_RANGE): 
    # https://numpy.org/doc/stable/reference/random/generated/numpy.random.poisson.html
    # The Poisson distribution is the limit of the binomial distribution for large N.
    sample_1 = [1 if r < P1 else 0 for r in [random.random() for i in range(Y_RANGE)]]
    sample_2 = [1 if r < P2 else 0 for r in [random.random() for i in range(Y_RANGE)]]
    sample_3 = [1 if r < P3 else 0 for r in [random.random() for i in range(Y_RANGE)]]

    distr_1.loc[i] = sample_1.count(1)
    distr_2.loc[i] = sample_2.count(1)
    distr_3.loc[i] = sample_3.count(1)
    ...

Результат работы:

(к оглавлению)

3. Экспоненциальное распределение

Схема формирования выборок и получения искомых величин: заполняем 1000 массивов размером единицами с вероятностью (в данном случае p = 0.1 ), остальные позиции заполняем нулями. Количества нулей между единицами (успехами) в каждом массиве являются искомыми случайными величинами, формирующими Экспоненциальное распределение. Нули в данном случае играют роль "интервала времени" между "событиями" ("успехами", единицами).

Основная часть программы для получения выборок и искомых величин (полный код программы):

X_RANGE = 1000 # 1000 выборок
Y_RANGE = 20   # берём выборку размером 20

LAMBDA_1 = 1 # в среднем 1 успех за условный интервал веремени (выборку)
LAMBDA_2 = 2 # в среднем 2 успеха за условный интервал веремени (выборку)
LAMBDA_3 = 3 # в среднем 3 успеха за условный интервал веремени (выборку)

P1 = LAMBDA_1 / Y_RANGE # вероятность успеха для LAMBDA_1
P2 = LAMBDA_2 / Y_RANGE # вероятность успеха для LAMBDA_2
P3 = LAMBDA_3 / Y_RANGE # вероятность успеха для LAMBDA_3

THETA_1 = (Y_RANGE - LAMBDA_1)/LAMBDA_1 # средний интервал времени между успехами
                                        # (например, 1 успех из 1000 замеров даёт средний интервал 999)
THETA_2 = (Y_RANGE - LAMBDA_2)/LAMBDA_2 # средний интервал времени между успехами 
                                        # (например, 2 успеха из 1000 замеров даёт средний интервал 499)
THETA_3 = (Y_RANGE - LAMBDA_3)/LAMBDA_3 # средний интервал времени между успехами
                                        # (например, 3 успеха из 1000 замеров даёт средний интервал ~332)
...
# Пример: 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1
# Число успехов: 4
# Время между успехами: [3, 8, 4] 
def calc_times(sample: list, df: pd.DataFrame, remainder: int):
    time = remainder
    for event in sample:
        if event == 1:
            df.loc[len(df), 'time'] = time
            time = 0
        elif event == 0:
            time += 1
    return df, time

remainder1 = 0
remainder2 = 0
remainder3 = 0
for i in range(X_RANGE): 
    # https://numpy.org/doc/stable/reference/random/generated/numpy.random.poisson.html
    # The Poisson distribution is the limit of the binomial distribution for large N.
    sample_1 = [1 if r < P1 else 0 for r in [random.random() for i in range(Y_RANGE)]]
    sample_2 = [1 if r < P2 else 0 for r in [random.random() for i in range(Y_RANGE)]]
    sample_3 = [1 if r < P3 else 0 for r in [random.random() for i in range(Y_RANGE)]]

    distr_1, remainder1 = calc_times(sample_1, distr_1, remainder1)
    distr_2, remainder2 = calc_times(sample_2, distr_2, remainder2)
    distr_3, remainder3 = calc_times(sample_3, distr_3, remainder3)
    ...

Результат работы:

(к оглавлению)

4. Распределение Вейбулла

Схема формирования выборок и получения искомых величин: заполняем 1000 массивов размером единицами с вероятностью (в данном случае p = 0.1 ), остальные позиции заполняем нулями. Количества нулей между единицами (успехами) в каждом массиве, возведённые в степень , являются искомыми случайными величинами, формирующими распределение Вейбулла. Нули в данном случае играют роль "интервала времени" между "событиями" ("успехами", единицами), а меняющаяся интенсивность "событий" отражается степенью .

Основная часть программы для получения выборок и искомых величин (полный код программы):

X_RANGE = 1000 # 1000 выборок
Y_RANGE = 1000 # берём выборку размером 1000

LAMBDA_1 = 1 # в среднем 1 успех за условный интервал веремени (выборку)
LAMBDA_2 = 2 # в среднем 2 успеха за условный интервал веремени (выборку)
LAMBDA_3 = 3 # в среднем 3 успеха за условный интервал веремени (выборку)

P1 = LAMBDA_1 / Y_RANGE # вероятность успеха для LAMBDA_1
P2 = LAMBDA_2 / Y_RANGE # вероятность успеха для LAMBDA_2
P3 = LAMBDA_3 / Y_RANGE # вероятность успеха для LAMBDA_3

THETA_1 = (Y_RANGE - LAMBDA_1)/LAMBDA_1 # средний интервал времени между успехами
                                        # (например, 1 успех из 1000 замеров даёт средний интервал 999)
THETA_2 = (Y_RANGE - LAMBDA_2)/LAMBDA_2 # средний интервал времени между успехами 
                                        # (например, 2 успеха из 1000 замеров даёт средний интервал 499)
THETA_3 = (Y_RANGE - LAMBDA_3)/LAMBDA_3 # средний интервал времени между успехами
                                        # (например, 3 успеха из 1000 замеров даёт средний интервал ~332)

BETA_1 = 3.0
BETA_2 = 1.5 
BETA_3 = 0.9 

K_1 = 1/BETA_1 # степень, в которую будет возведено каждое полученное значение времени
K_2 = 1/BETA_2 # степень, в которую будет возведено каждое полученное значение времени
K_3 = 1/BETA_3 # степень, в которую будет возведено каждое полученное значение времени
...
# Пример: 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1
# Число успехов: 4
# Время между успехами: [3, 8, 4] 
def calc_times(sample: list, df: pd.DataFrame, remainder: int):
    time = remainder
    for event in sample:
        if event == 1:
            df.loc[len(df), 'time'] = time
            time = 0
        elif event == 0:
            time += 1
    return df, time

remainder1 = 0
remainder2 = 0
remainder3 = 0
for i in range(X_RANGE): 
    # https://numpy.org/doc/stable/reference/random/generated/numpy.random.poisson.html
    # The Poisson distribution is the limit of the binomial distribution for large N.
    sample_1 = [1 if r < P1 else 0 for r in [random.random() for i in range(Y_RANGE)]]
    sample_2 = [1 if r < P2 else 0 for r in [random.random() for i in range(Y_RANGE)]]
    sample_3 = [1 if r < P3 else 0 for r in [random.random() for i in range(Y_RANGE)]]

    distr_1, remainder1 = calc_times(sample_1, distr_1, remainder1)
    distr_2, remainder2 = calc_times(sample_2, distr_2, remainder2)
    distr_3, remainder3 = calc_times(sample_3, distr_3, remainder3)

    # https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.weibull_min.html
    # Suppose X is an exponentially distributed random variable with scale s. 
    # Then Y = X**k is weibull_min distributed with shape c = 1/k and scale s**k.
    distr_1_pow_k = np.power(distr_1.values, K_1)
    distr_2_pow_k = np.power(distr_2.values, K_2)
    distr_3_pow_k = np.power(distr_3.values, K_3)
    ...

Результат работы:

(к оглавлению)

5. Гамма-распределение

Схема формирования выборок и получения искомых величин: заполняем 1000 массивов размером единицами с вероятностью (в данном случае p = 0.1 ), остальные позиции заполняем нулями. Количества нулей между единицами (успехами) в каждом массиве, являются искомыми случайными величинами, формирующими Гамма-распределение. Нули в данном случае играют роль "интервала времени" между "событиями" ("успехами", единицами).

Основная часть программы для получения выборок и искомых величин (полный код программы):

X_RANGE = 1000 # 1000 выборок
Y_RANGE = 20   # берём выборку размером 20

LAMBDA_1 = 1 # в среднем 1 успех за условный интервал веремени (выборку)
LAMBDA_2 = 2 # в среднем 2 успеха за условный интервал веремени (выборку)
LAMBDA_3 = 3 # в среднем 3 успеха за условный интервал веремени (выборку)

P1 = LAMBDA_1 / Y_RANGE # вероятность успеха для LAMBDA_1
P2 = LAMBDA_2 / Y_RANGE # вероятность успеха для LAMBDA_2
P3 = LAMBDA_3 / Y_RANGE # вероятность успеха для LAMBDA_3

THETA_1 = (Y_RANGE - LAMBDA_1)/LAMBDA_1 # средний интервал времени между успехами
                                        # (например, 1 успех из 1000 замеров даёт средний интервал 999)
THETA_2 = (Y_RANGE - LAMBDA_2)/LAMBDA_2 # средний интервал времени между успехами 
                                        # (например, 2 успеха из 1000 замеров даёт средний интервал 499)
THETA_3 = (Y_RANGE - LAMBDA_3)/LAMBDA_3 # средний интервал времени между успехами
                                        # (например, 3 успеха из 1000 замеров даёт средний интервал ~332)

K_1 = 3 # количество "успехов" для которого считается интервал времени
K_2 = 2 # количество "успехов" для которого считается интервал времени
K_3 = 1 # количество "успехов" для которого считается интервал времени
...
# Пример: 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1
# Число успехов: 4
# Время между успехами: [3, 8, 4] 
def calc_times(sample: list, df: pd.DataFrame, remainder: int):
    time = remainder
    for event in sample:
        if event == 1:
            df.loc[len(df), 'time'] = time
            time = 0
        elif event == 0:
            time += 1
    return df, time

remainder1 = 0
remainder2 = 0
remainder3 = 0
for i in range(X_RANGE): 
    # https://numpy.org/doc/stable/reference/random/generated/numpy.random.poisson.html
    # The Poisson distribution is the limit of the binomial distribution for large N.
    sample_1 = [1 if r < P1 else 0 for r in [random.random() for i in range(Y_RANGE)]]
    sample_2 = [1 if r < P2 else 0 for r in [random.random() for i in range(Y_RANGE)]]
    sample_3 = [1 if r < P3 else 0 for r in [random.random() for i in range(Y_RANGE)]]

    distr_1, remainder1 = calc_times(sample_1, distr_1, remainder1)
    distr_2, remainder2 = calc_times(sample_2, distr_2, remainder2)
    distr_3, remainder3 = calc_times(sample_3, distr_3, remainder3)

    distr_1_k = [np.sum(distr_1.values[K_1*i: K_1*i+K_1]) for i in range(int(len(distr_1)/K_1))]
    distr_2_k = [np.sum(distr_2.values[K_2*i: K_2*i+K_2]) for i in range(int(len(distr_2)/K_2))]
    distr_3_k = [np.sum(distr_3.values[K_3*i: K_3*i+K_3]) for i in range(int(len(distr_3)/K_3))]
    ...

Результат работы:

(к оглавлению)

6. Бета-распределение

Схема формирования выборок и получения искомых величин: Воспользуемся уже готовыми функциями для генерации случайных величин из Гамма-распределения stats.gamma.rvs(a, size). Получим 1000 значений $X \sim Gamma(1,1)$ и 1000 значений $Y \sim Gamma(9,1)$ . Тогда искомые значения из Бета-распределения будут вычеслены по формуле:

$\frac{X}{X+Y} \sim Beta(1,9).$

Основная часть программы для получения выборок и искомых величин (полный код программы):

X_RANGE = 1000

K_1 = 1 # 1-я пара
K_2 = 9 # 1-я пара
K_3 = 2 # 2-я пара
K_4 = 4 # 2-я пара
K_5 = 0.5 # 3-я пара
K_6 = 0.5 # 3-я пара
...
# Генерируем массивы случайных величин из Гамма-распределений
# 0: [0 .. 999]
# 1: [0 .. 999]
# ..
# 7: [0 .. 999]
gamma = []
gamma.append(stats.gamma.rvs(a=K_1, size=X_RANGE))
gamma.append(stats.gamma.rvs(a=K_2, size=X_RANGE))
gamma.append(stats.gamma.rvs(a=K_3, size=X_RANGE))
gamma.append(stats.gamma.rvs(a=K_4, size=X_RANGE))
gamma.append(stats.gamma.rvs(a=K_5, size=X_RANGE))
gamma.append(stats.gamma.rvs(a=K_6, size=X_RANGE))
# Транспонируем матрицу случайных величин - строка будет выдавать случайные величины для каждой итерации цикла for
# 0: [0 .. 7]
# 1: [0 .. 7]
# ..
# 999: [0 .. 7]
gamma = np.array(gamma).transpose().tolist()

for i in range(X_RANGE):
    ########### 
    x00 = [gamma[i][0], gamma[i][1]]
    beta_0 = (x00[0]) / (x00[0] + x00[1])
    ...
    ########### 
    x01 = [gamma[i][2], gamma[i][3]]
    beta_1 = (x01[0]) / (x01[0] + x01[1])
    ...
    ########### 
    x02 = [gamma[i][4], gamma[i][5]]
    beta_2 = (x02[0]) / (x02[0] + x02[1])
    ...
    ###########
    betas_0.append(beta_0)
    betas_1.append(beta_1)
    betas_2.append(beta_2)
    ...

Результат работы:

(к оглавлению)

7. Гипергеометрическое распределение

Схема формирования выборок и получения искомых величин: рассмотрим на примере колоды карт. Допустим есть колода из N=52 карт. Нас интересует количество вытянутых червей и пик, если вытягивать из колоды по n=5 карт. Общее количество интересующих нас карт в колоде K=26 (13 карт червовой масти и 13 карт пиковой). Количества вытянутых червей и пик при данных условиях - это искомые значения из Гипергеометрического распределения HG(52, 26, 5) .

Картинки с картами взяты у Kenney (CC0)

Основная часть программы для получения выборок и искомых величин (полный код программы):

cards = pd.DataFrame([
    ['C', '2'], ['D', '2'], ['H', '2'], ['S', '2'],
    ['C', '3'], ['D', '3'], ['H', '3'], ['S', '3'],
    ['C', '4'], ['D', '4'], ['H', '4'], ['S', '4'],
    ['C', '5'], ['D', '5'], ['H', '5'], ['S', '5'],
    ['C', '6'], ['D', '6'], ['H', '6'], ['S', '6'],
    ['C', '7'], ['D', '7'], ['H', '7'], ['S', '7'],
    ['C', '8'], ['D', '8'], ['H', '8'], ['S', '8'],
    ['C', '9'], ['D', '9'], ['H', '9'], ['S', '9'],
    ['C', '10'], ['D', '10'], ['H', '10'], ['S', '10'],
    ['C', 'J'], ['D', 'J'], ['H', 'J'], ['S', 'J'],
    ['C', 'Q'], ['D', 'Q'], ['H', 'Q'], ['S', 'Q'],
    ['C', 'K'], ['D', 'K'], ['H', 'K'], ['S', 'K'],
    ['C', 'A'], ['D', 'A'], ['H', 'A'], ['S', 'A'],
], columns=['Suit', 'Rank'])

CARDS_1 = 5 # Выбираем 5 карт из колоды
CARDS_2 = 15 # Выбираем 15 карт из колоды
CARDS_3 = 25 # Выбираем 25 карт из колоды

N = len(cards) # Размер совокупности
S_COUNT = cards['Suit'].values.tolist().count('S') # Число пик в колоде
H_COUNT = cards['Suit'].values.tolist().count('H') # Число червей в колоде
X_RANGE = 1000 # Число выборок
...
for i in range(X_RANGE):
    sample_1 = cards.sample(CARDS_1)
    sample_2 = cards.sample(CARDS_2)
    sample_3 = cards.sample(CARDS_3)

    distr_1.loc[i] = sample_1['Suit'].values.tolist().count('S')
    distr_1.loc[i] += sample_1['Suit'].values.tolist().count('H')
    distr_2.loc[i] = sample_2['Suit'].values.tolist().count('S')
    distr_2.loc[i] += sample_2['Suit'].values.tolist().count('H')
    distr_3.loc[i] = sample_3['Suit'].values.tolist().count('S')
    distr_3.loc[i] += sample_3['Suit'].values.tolist().count('H')
    ...

Результат работы:

(к оглавлению)

8. Нормальное распределение

Схема формирования выборок и получения искомых величин: согласно Центральной Предельной Теореме "Если величина является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то центрированное и нормированное распределение такой величины при достаточно большом числе слагаемых стремится к нормальному распределению." [ссылка]. Если для популяции raw_data со средним $\mu$ и стандартным отклонением 1000 раз взять выборку размера и расчитать среднее значение $\overline{x}$ каждой выборки, полученные значения сформируют Нормальное распределение.

Основная часть программы для получения выборок и искомых величин (полный код программы):

mean = raw_data.mean() # μ - среднее всей совокупности
std = raw_data.std()   # σ - стандартное отклонение всей совокупности

se_05 = std / math.sqrt(5)  # Стандартная ошибка (SE05) для выборки размером 5
se_20 = std / math.sqrt(20) # Стандартная ошибка (SE20) для выборки размером 20
...
for i in range(1000): 
    sample_05 = raw_data.sample(5)
    sample_20 = raw_data.sample(20)
    ...
    sample_mean_05.loc[i] = [sample_05.mean()] # x̄ - среднее выборки размером 5
    sample_mean_20.loc[i] = [sample_20.mean()] # x̄ - среднее выборки размером 20
    ...
    z_sample_mean_05 = (sample_mean_05['mean_05'] - mean) / se_05 - 1 # -1, чтобы разделить графики распределений
    z_sample_mean_20 = (sample_mean_20['mean_20'] - mean) / se_20 + 1 # +1, чтобы разделить графики распределений
    ...

Результат работы:

(к оглавлению)

9. Распределение Стьюдента (t-распределение)

Схема формирования выборок и получения искомых величин: в отличии от Нормального распределения для Распределения Стьюдента неизвестно стандартное отклонение популяции , поэтому расчёт стандартной ошибки среднего (SE или SEM) проводится с помощью стандартного отклонения самой выборки. В остальном действия те же, что и для Нормального распределения: если для популяции raw_data со средним $\mu$ 1000 раз взять выборку размера и расчитать среднее значение $\overline{x}$ каждой выборки, полученные значения сформируют t-распределение со сдвигом $\mu$ , масштабом равным оценке стандартной ошибки среднего (SEE), рассчитанной с помощью , и степенью свободы n-1 .

Основная часть программы для получения выборок и искомых величин (полный код программы):

mean = raw_data.mean() # μ - среднее всей совокупности
...
SAMPLE_SIZE_1 = 3  # размер первой выборки
SAMPLE_SIZE_2 = 50 # размер второй выборки
...
for i in range(1000): 
    sample_1 = raw_data.sample(SAMPLE_SIZE_1)
    sample_2 = raw_data.sample(SAMPLE_SIZE_2)

    # https://en.wikipedia.org/wiki/Standard_error#Estimate
    see_1 = sample_1.std() / math.sqrt(SAMPLE_SIZE_1) # используем стандартное отклоненение выборки (s) взамен стандартного отклонения совокупности (σ)
    see_2 = sample_2.std() / math.sqrt(SAMPLE_SIZE_2) # используем стандартное отклоненение выборки (s) взамен стандартного отклонения совокупности (σ)
    ...
    sample_mean_1.loc[i] = [sample_1.mean()]
    sample_mean_2.loc[i] = [sample_2.mean()]
    ...
    sample_see_1.loc[i] = [see_1] # оценка стандартной ошибки для выборки n=3
    sample_see_2.loc[i] = [see_2] # оценка стандартной ошибки для выборки n=50
    ...
    # https://en.wikipedia.org/wiki/Student%27s_t-test#One-sample_t-test
    t_sample_mean_1.loc[i] = ((sample_1.mean() - mean) / see_1) - 1 # -1, чтобы разделить графики распределений
    t_sample_mean_2.loc[i] = ((sample_2.mean() - mean) / see_2) + 1 # +1, чтобы разделить графики распределений

Результат работы:

(к оглавлению)

10. Распределение Хи-квадрат

Схема формирования выборок и получения искомых величин: Воспользуемся уже готовыми функциями для генерации случайных величин из Стандартного Нормального распределения stats.norm.rvs(size). Получим 1000 значений для каждого $Z_{i}$ , где $Z_{i} \sim N(0,1), i \in 0,...,k$ , где - это число степеней свободы. Тогда искомые значения из Хи-квадрат распределения будут вычеслены по формуле:

$Q = \sum_{i=1}^k Z_i^2 \sim \chi^2(k).$

Основная часть программы для получения выборок и искомых величин (полный код программы):

X_RANGE = 1000

DF_1 = 2
DF_2 = 3
DF_3 = 8
...
# Генерируем массивы нормально распределённых случайных величин
# 0: [0 .. 999]
# 1: [0 .. 999]
# ..
# 7: [0 .. 999]
normal = [stats.norm.rvs(size=X_RANGE) for i in range(max(DF_1, DF_2, DF_3))]
# Транспонируем матрицу случайных величин - строка будет выдавать случайные величины для каждой итерации цикла for
# 0: [0 .. 7]
# 1: [0 .. 7]
# ..
# 999: [0 .. 7]
normal = np.array(normal).transpose().tolist()
for i in range(X_RANGE):
    ########### Число степеней свободы 1
    x00 = normal[i][0: DF_1] # Массив случайных величин [Z1, Z2]
    chi_squared_0 = np.sum(np.square(x00)) # Берём квадрат случайных величин и суммируем
    ...
    ########### Число степеней свободы 2
    x01 = normal[i][0: DF_2] # Массив случайных величин [Z1, Z2, Z3]
    chi_squared_1 = np.sum(np.square(x01)) # Берём квадрат случайных величин и суммируем
    ...
    ########### Число степеней свободы 3
    x02 = normal[i][0: DF_3] # Массив случайных величин [Z1, Z2, Z3, Z4, Z5, Z6, Z7, Z8]
    chi_squared_2 = np.sum(np.square(x02)) # Берём квадрат случайных величин и суммируем
    ...
    ###########
    chis_0.append(chi_squared_0)
    chis_1.append(chi_squared_1)
    chis_2.append(chi_squared_2)
    ...

Результат работы:

(к оглавлению)

11. Распределение Фишера

Схема формирования выборок и получения искомых величин: Воспользуемся уже готовыми функциями для генерации случайных величин из Хи-квадрат распределения stats.chi2.rvs(df, size). Получим 1000 значений для $S_{1} \sim \chi^2(d_{1})$ и для $S_{2} \sim \chi^2(d_{2})$ . Тогда искомые значения из распределения Фишера будут вычеслены по формуле:

$X = \frac{S_1/d_1}{S_2/d_2} \sim \mathrm{F}(d_1,d_2).$

Основная часть программы для получения выборок и искомых величин (полный код программы):

X_RANGE = 1000

DF_1 = 1 # 1-я пара
DF_2 = 9 # 1-я пара
DF_3 = 2 # 2-я пара
DF_4 = 4 # 2-я пара
DF_5 = 3 # 3-я пара
DF_6 = 5 # 3-я пара
...
# Генерируем массивы случайных величин из Хи-квадрат распределений
# 0: [0 .. 999]
# 1: [0 .. 999]
# ..
# 7: [0 .. 999]
chi2 = []
chi2.append(stats.chi2.rvs(df=DF_1, size=X_RANGE))
chi2.append(stats.chi2.rvs(df=DF_2, size=X_RANGE))
chi2.append(stats.chi2.rvs(df=DF_3, size=X_RANGE))
chi2.append(stats.chi2.rvs(df=DF_4, size=X_RANGE))
chi2.append(stats.chi2.rvs(df=DF_5, size=X_RANGE))
chi2.append(stats.chi2.rvs(df=DF_6, size=X_RANGE))
# Транспонируем матрицу случайных величин - строка будет выдавать случайные величины для каждой итерации цикла for
# 0: [0 .. 7]
# 1: [0 .. 7]
# ..
# 999: [0 .. 7]
chi2 = np.array(chi2).transpose().tolist()

for i in range(X_RANGE):
    ########### 
    x00 = [chi2[i][0], chi2[i][1]]
    f_0 = (x00[0] / DF_1) / (x00[1] / DF_2)
    ...
    ########### 
    x01 = [chi2[i][2], chi2[i][3]]
    f_1 = (x01[0] / DF_3) / (x01[1] / DF_4)
    ...
    ########### 
    x02 = [chi2[i][4], chi2[i][5]]
    f_2 = (x02[0] / DF_5) / (x02[1] / DF_6)
    ...
    ###########
    fs_0.append(f_0)
    fs_1.append(f_1)
    fs_2.append(f_2)
    ...

Результат работы:

(к оглавлению)

Заключение

Распределения вероятностей являются результатом большого количества наблюдений и экспериментов статистиков прошлых столетий. Это важно отметить, т. к. расчёты того времени предполагали отсутствие всякого рода вычислительной техники, поэтому главная роль распределений стала аппроксимация любого рода случайных величин. Для самых разных задач и данных существует множество статистических тестов и критериев, в основе которых лежат основные распределения. Примерами наиболее известных из них являются:

Z-тест, основанный на нормальном распределении
t-критерий Стьюдента, основанный на распределении Стьюдента
Критерий хи-квадрат, связанный с распределением Хи-квадрат
F-тест, основанный на распределении Фишера (F-распределении)

Основной областью применения этих тестов является проверка статистических гипотез, потому что они позволяют стандартизировать и проводить количественную оценку полученных сырых данных, а также проводить сравнения нескольких наборов данных для различных условий и вариантов использования (гипотез).

Теги:

Хабы:

Если эта публикация вас вдохновила и вы хотите поддержать автора — не стесняйтесь нажать на кнопку

Основные типы распределений вероятностей в примерах

Список распределений вероятностей

1. Биномиальное распределение

2. Распределение Пуассона

3. Экспоненциальное распределение

4. Распределение Вейбулла

5. Гамма-распределение

6. Бета-распределение

7. Гипергеометрическое распределение

8. Нормальное распределение

9. Распределение Стьюдента (t-распределение)

10. Распределение Хи-квадрат

11. Распределение Фишера

Заключение

Публикации

Истории

Работа

Ближайшие события