Несмотря на огромную популярность аппарата графических моделей для решения задачи структурной классификации, задача настройки их параметров по обучающей выборке долгое время оставалась открытой. В своем докладе Дмитрий Ветров, рассказал об обобщении метода опорных векторов и некоторых особенностях его применения для настройки параметров графических моделей. Дмитрий – руководитель группы Байесовских методов, доцент ВМК МГУ и преподаватель в ШАДе.
Видеозапись доклада.
План доклада:
Сама концепция машинного обучения довольно несложная – это, если говорить образно, поиск взаимосвязей в данных. Данные представляются в классической постановке набором объектов, взятых из одной и той же генеральной совокупности, у каждого объекта есть наблюдаемые переменные, есть скрытые переменные. Наблюдаемые переменные (дальше будем их обозначать X) часто называются признаками, соответственно, скрытые переменные (T) — это те, которые подлежат определению. Для того, чтобы эту взаимосвязь между наблюдаемыми и скрытыми переменными установить, предполагается, что у нас есть обучающая выборка, т.е. набор объектов, для которых известны и наблюдаемые и скрытые компоненты. Глядя на нее, мы пытаемся настроить некоторые решающие правила, которые нам позволят в дальнейшем, когда мы видим набор признаков, оценить скрытые компоненты. Процедура обучения приблизительно выглядит следующим образом: фиксируется множество допустимых решающих правил, которые как правило задаются с помощью весов (W), а дальше каким-то образом в ходе обучения эти веса настраиваются. Тут же с неизбежностью возникает проблема переобучения, если у нас слишком богатое семейство допустимых решающих правил, то в процессе обучения мы легко можем выйти на случай, когда для обучающей выборки мы прекрасно прогнозируем ее скрытую компоненту, а вот для новых объектов прогноз оказывается плохой. Исследователями в области машинного обучения было потрачено немало лет и усилий для того, чтобы эту проблему снять с повестки дня. В настоящее время, кажется, что худо-бедно это удалось.
Байесовская парадигма является подразделом машинного обучения, и в этом случае предполагается, что взаимосвязь между настраиваемыми параметрами W, наблюдаемыми переменными X и скрытыми переменными Т моделируется в виде некоторого совместного распределения, например, на все эти три группы переменных. Соответственно в классической постановке задач машинного обучения т.е., когда предполагается, что данные представляют из себя совокупность объектов, взятых из одной и той же генеральной совокупности независимых объектов, это совместное распределение можно представить вот в таком вот сравнительно простом виде:
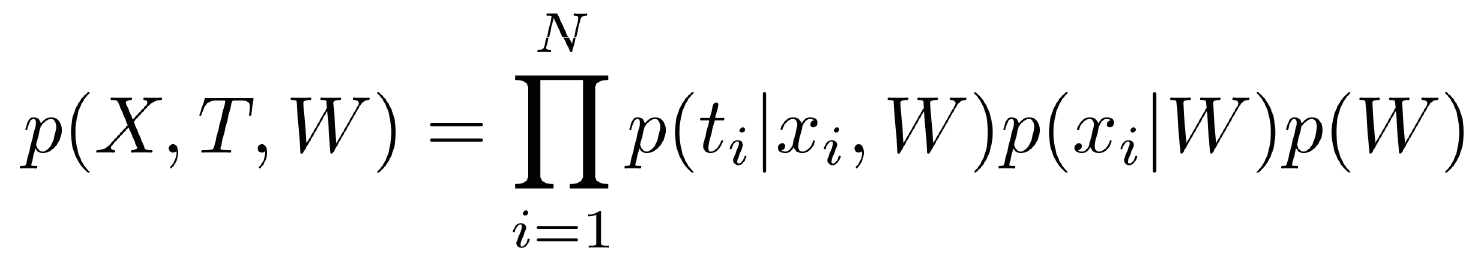
Первый множитель отвечает за распределение скрытой переменной при известных признаках и заданном решающем правиле. Второй множитель отвечает за распределение наблюдаемых переменных при заданном решающем правиле (так называемых дискриминативных моделях). Этот множитель нас не интересует, поскольку мы не моделируем распределение наблюдаемых переменных. Но более в общем случае так называемых генеративных моделей он имеет место быть. И, наконец, последний множитель, который неизбежно вытекает, если мы просто рассмотрим правило работы с вероятностями – это априорное распределение на веса W, т.е. на значения параметров решающего правила. И вот именно тот факт, что у нас появилась возможность задавать это априорное распределение, наверное, и явился ключевой причиной, почему Байесовские методы последние 10 лет переживает бум. Долгое время, до середины девяностых годов, Байесовский подход к теории вероятностей достаточно скептически воспринимался исследователями по той причине, что он предполагает, что мы каким-то образом должны задавать априорное распределение на параметры. И традиционный вопрос был – откуда его брать. Функция правдоподобия, понятно, определяется данными, а априорное распределение брать с потолка? Ясно что, если будем брать по-разному априорное распределение, будем получать в итоге разные результаты, применяя формулу Байеса. Поэтому долгое время Байесовский подход казался некоторой игрой ума. Тем не менее, примерно в середине девяностых годов пошел шквал работ, где доказывалось, что общие, стандартные методы машинного обучения можно существенно улучшить, если мы будем учитывать специфику решаемой задачи.
Оказалось, что специфика много где есть, вроде как все задачи сводятся к стандартным постановкам, но в большинстве случаев есть некоторая специфика, некоторые априорные предпочтения на ту или иную форму решающего правила. Т.е. фактически предпочтения на те или иные значения весов W. И тогда возник вопрос, как это можно объединить с качеством работы решающего правила на обучающей выборке? Традиционно процедура машинного обучения выглядит как минимизация ошибки на обучении, т.е. мы пытаемся построить решающее правило так, чтобы как можно точнее прогнозировать переменные Т для обучающей выборки, для которой они известны. Т.е. мы можем оценить качество. Это один показатель. Другой показатель заключается в том, что мы считаем, некоторые значения W более предпочтительными.
Как это все можно увязать в единых терминах? Оказалось, что в рамках Байесовской парадигмы это возможно. Качественное на обучении характеризуется функцией правдоподобия, которая есть вероятностный смысл, а предпочтение на параметры характеризуется априорным распределением. Соответственно, функция правдоподобия и априорное распределение отлично сочетаются в рамках формулы Байеса и приводят к апостериорным распределениям на значения параметров W, которые мы в ходе обучения настраиваем. Тем самым Байесовская парадигма дала возможность корректно в единых терминах скомбинировать как точность обучающей выборки, так и наши априорные предпочтения на значения весов, которые в очень многих прикладных задачах достаточно органично возникали, и, соответственно, введение этих априорных предпочтений позволило существенно поднять качество получаемых решающих правил. Кроме того, с конца девяностых и в нулевые годы появились более продвинутые средства, которые позволяют еще и априорное распределение некоторым хитрым образом параметризовать и настраивать по данным. Т.е. на кнопку нажал, и автоматически настроилось априорное распределение, наиболее подходящее для данной задачи, после чего пошла процедура машинного обучения.
Эти методы уже неплохо разработаны. Не будет сильным преувеличением сказать, что классическая постановка задачи машинного обучения решена. И как это часто бывает в жизни, как только мы закрыли классическую постановку, тут же оказалось, что нас больше интересуют неклассические постановки, которые оказались гораздо более богаты и интересны. Неклассическая постановка в даном случае — это ситуация, когда скрытые переменные объектов оказываются взаимозависимы. Т.е. мы не можем определить скрытую переменную каждого объекта, глядя только на признаки этого объекта, как предполагалось в традиционной задаче машинного обучения. Более того, она зависит не только и не столько от признаков других объектов, сколько от скрытых переменных других объектов. Соответственно, мы не можем определять скрытую переменную каждого объекта независимо, только в совокупности. Ниже я приведу большое количество примеров задач с взаимосвязанными скрытыми компонентами. Можно заметить, что эти взаимосвязи, т.е. осознание того факта, что скрытые переменные в нашей выборке взаимозависимы, открывает широчайшие возможности для дополнительной регуляризации задач. Т.е. в конечном итоге для дальнейшего поднятия точности решения.
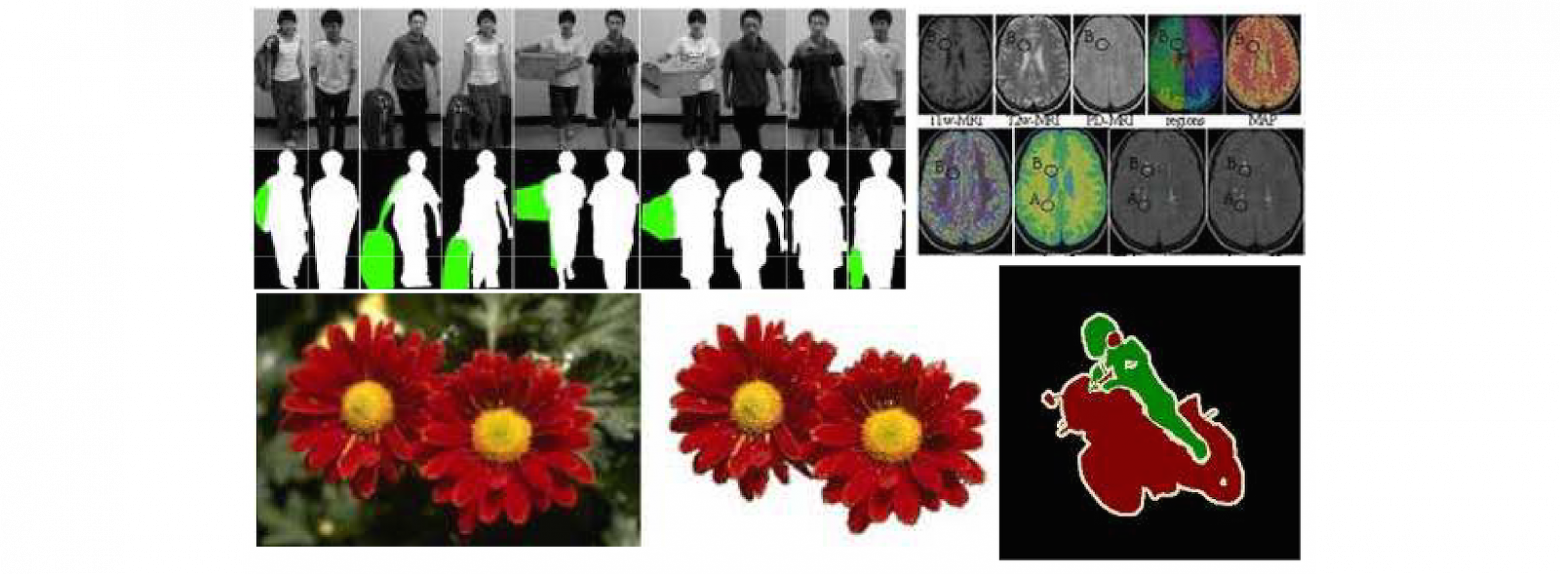
Первый наиболее классический пример — сегментация изображений. Это средство, которое решать такие задачи с взаимозависимыми скрытыми переменными, с него, собственно и начался бум графических моделей. Задача стала крайне востребована с развитием цифровых камер. Что это такое? Для каждого пикселя мы пытаемся поставить некоторую метку класса. В простейшем случае с бинарной сегментацией мы пытаемся отделись объект от фона. В более сложных случаях мы пытаемся для объектов еще и какую-то семантику привнести. В принципе, эту задачу можно рассматривать как стандартную задачу классификации. Каждый пиксель является объектом, каждый пиксель может принадлежать к одному из К классов, у каждого пикселя есть определенный набор признаков. В простейшем случае это цвет, можно снять текстурные признаки, какую-то контекстную информацию, но представляется достаточно очевидным, что в данном случае у нас есть некоторая специфика. Соседние пиксели скорее всего принадлежат к одному и тому же классу, просто потому что в задаче сегментации мы предполагаем, что у нас результатом сегментации будут некоторые компактные области. Как только мы попытаемся этот факт формализовать, у нас неизбежно вытекает, что мы не можем каждый пиксель классифицировать или сегментировать в отрыве от всего остального, мы можем сегментировать только всю картинку сразу. Вот простейшая задача, в которой появились взаимозависимости между скрытыми переменными.

Следующая задача — видиотрекинг. Мы можем каждый кадр обрабатывать независимо, скажем, искать или идентифицировать пешеходов, идентифицировать пешеходов. Или делать трекинг мышей. Мыши сверху выглядят очень похоже, тречить их нужно так, чтобы еще каждая мышь идентифицировалась безошибочно. Попытки поставить цветные штрихи на шерсть жестко пресекаются биологами, которые утверждают, что мышь после этого будет в состоянии стресса. Соответственно, мыши все одинаковы, необходимо в каждый момент времени знать, где какая мышь у нас находится, чтобы анализировать их поведение. Ясно, что по отдельному кадру мы задачу решить не в состоянии. Нам необходимо учитывать соседние кадры, желательно в большом количестве. У нас снова возникают взаимозависимости между скрытыми переменными, где в качестве скрытой переменной выступает идентификатор мыши.
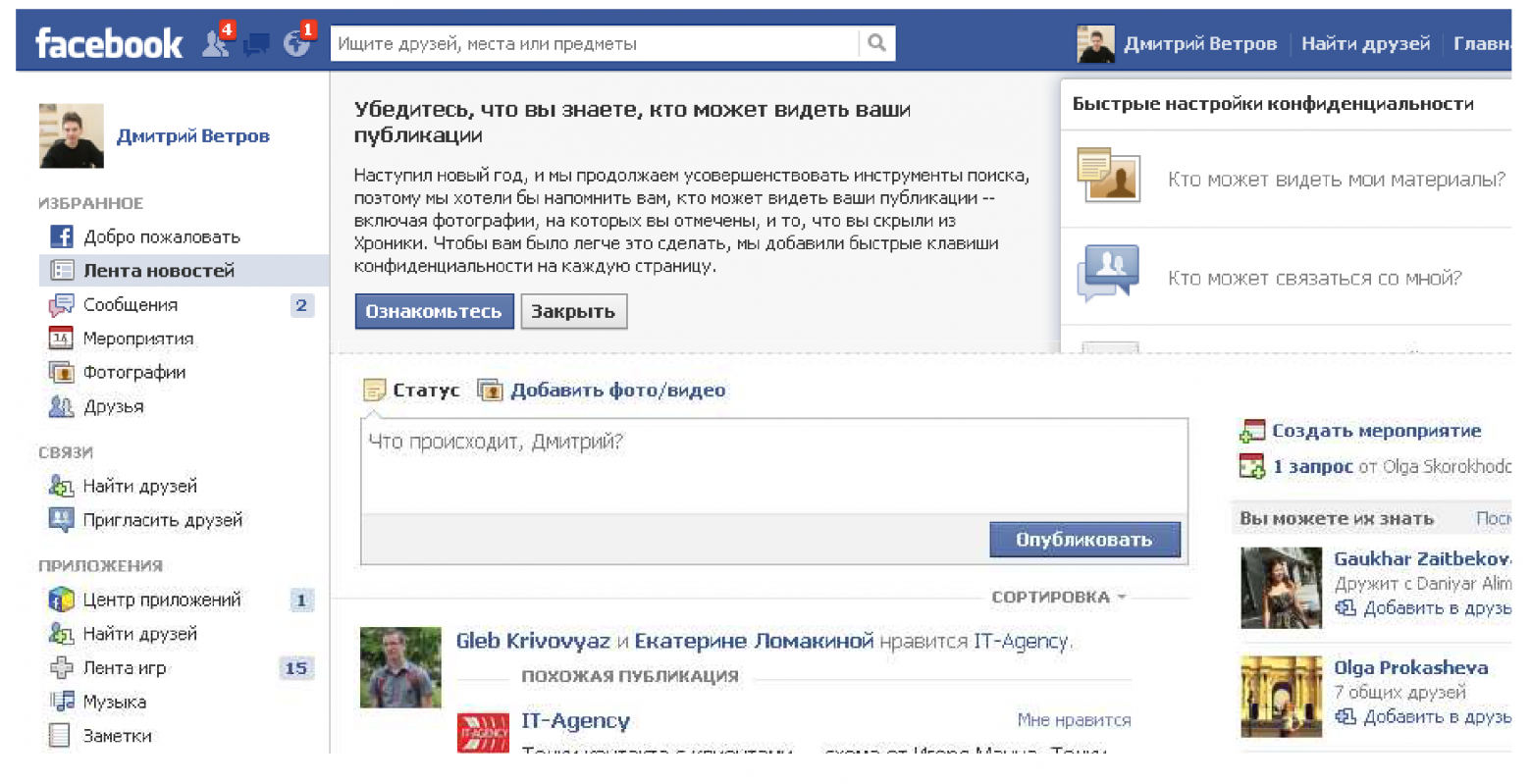
Анализ социальных сетей сейчас – вполне очевидная задача. Каждого пользователя социальных сетей, конечно, можно анализировать независимо от других, но очевидно, что мы при этом потеряем значительный пласт информации. Например, мы пытаемся анализировать пользователей на предмет их оппозиционности действующему режиму. Если у меня стоит баннер «Навального в президенты!» или «Навального в мэры!», меня, конечно, можно идентифицировать как оппозиционера, но если я более осторожно к этому подхожу и подобные баннеры не вывешиваю, то определить, что я симпатизирую оппозиции, можно только проанализировав моих друзей менее осторожных, которые эти баннеры радостно развешивают. Если окажется, что я с большим количеством таких людей нахожусь в статусе друзей, то вероятность того, что я сам тоже симпатизирую этим течениям, несколько повышается. Ну а если уйти от подобной гбшной тематики, то, допустим, ту же задачу адресной рекламы можно решить гораздо лучше, если мы будем задействовать не только данные про конкретного пользователя (скажем, анкетные данные, которые он сообщил у себя на страничке), но и глядя на круг его друзей.

Следующая задача — это регистрация изображений для построения трехмерных моделей по изображению, вписывания изображения в двух- или трехмерную модель. Данная задача предполагает, что изображения подвергаются некоторым деформациям при регистрации. Мы, конечно, можем пытаться для каждого пикселя искать деформацию независимо от других, но ясно, что в этом случае никакой эластичной деформации мы не получим, результат будет довольно плачевный. Хотя формально мы каждый пиксель куда-то впишем, и погрешность для каждого пикселя будет минимальна. При этом все изображение у нас просто рассыплется, если каждый пиксель будет деформироваться независимо. В качестве одного из способов учета этих взаимозависимостей можно воспользоваться аппаратом графических моделей, который позволяет анализировать взаимозависимости скрытых переменных.
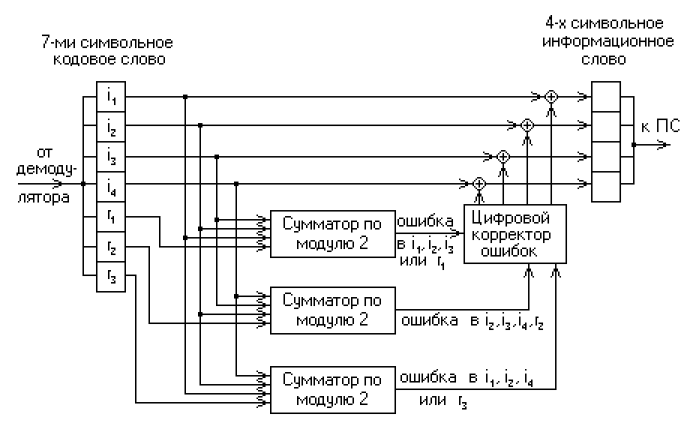
Есть еще одна важная задача. О ней не так часто упоминают, но на самом деле она весьма актуальна и, скорее всего, в ближайшие годы актуальность будет только возрастать. Это декодирование зашумленных сообщений. Сейчас мы окружены мобильными устройствами. Передача данных с их помощью не слишком надежна, каналы жутко перегружены. Очевидно, что потребность в трафике превышает текущие возможности, поэтому естественным образом возникает задача составить такой протокол, который с одной стороны был бы помехоустойчив, а с другой обладал высокой пропускной способностью. Тут мы сталкиваемся с любопытным явлением. Еще с пятидесятых годов прошлого века, когда Клодом Шенноном была разработана теория информации, известно, что для каждого канала связи существует некая предельная пропускная способность при заданной интенсивности помех.
Была выведена теоритическая формула. Больше информации, чем предсказывает теорема Шеннона, передать по зашумленному каналу нельзя в принципе. Но оказывается, что по мере приближения к этому теоритическому пределу, т.е. чем более эффективно мы пытаемся информацию передавать, применяя некоторые хитрые схемы архивации и добавление контрольных битов, которые как раз направлены на исправление ошибок, тем сложнее у нас схема декодирования этого сообщения. Т.е. наиболее эффективные помехоустойчивые коды крайне сложны в декодировке. Там не существует простых формул декодирования. Соответственно, если мы достигаем предела Шеннона, сложность декодирования возрастает экспоненциально. Закодировать и передать сообщение мы можем, а расшифровать его уже не в состоянии. Оказалось, что современные коды, разработанные и стандартизованные в нулевые годы (их сейчас используют в в большинстве мобильных устройств), близки к этому теоретически возможному пределу, и для их декодировки используются так называемый алгоритм передачи сообщений, основанный на алгоритме распространения доверия, который появился в теории графических моделей, возникшей в попытке решить задачу с взаимосвязанными скрытыми переменными.
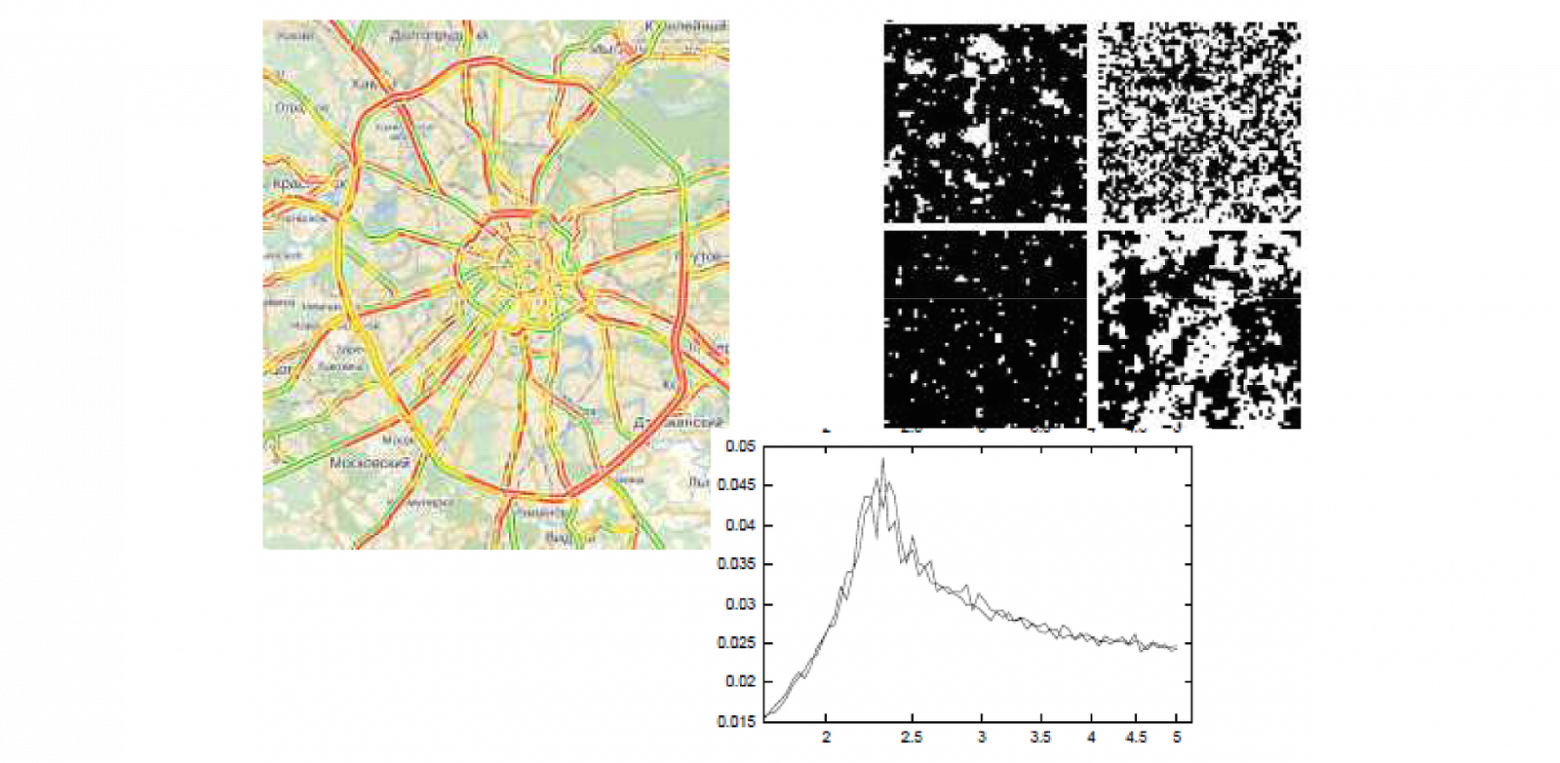
В конце девяностых также стала популярна задача, которую я условно назвал имитационным моделированием или моделированием агентских сред. Это попытка проанализировать поведение систем, состоящих из большого количества взаимодействующих агентов. Задача крайне интересная, строгих методов для ее решения не существует. Поэтому большинство этих задач решается с помощью симуляции методами Монте-Карло в различных модификациях. Простой пример – моделирование дорожного движения. В качестве агента выступают транспортные средства, ясно, что мы не можем моделировать поведение автомобилей вне контекста, так как все водители принимают решения, глядя на ближайших своих соседей по автотрассе. И оказалось, внесение в модель даже простейшего взаимодействия между автомобилистами, позволило получить потрясающий результат. Во-первых, было установлено сначала в теории, а потом и на практике, что есть некоторый критический предел интенсивности потока. Если поток превышает этот предел, то он становится метастабильным, т.е. неустойчивым. Малейшее отклонение от нормы (допустим, один из водителей чуть резче затормозил и сразу поехал дальше) приводит к тому, что тут же вырастают пробки на десятки километров. Это означает, что когда транспортный канал перегружен, он еще может функционировать без пробок, но пробка может возникнуть практически на ровном месте.
Сначала это получили в теории, потом убедились, что на практике действительно такое бывает. Действительно для каждой трассы, в зависимости от ее развязок, существует некая предельная пропускная способность, при которой поток еще движется стабильно. Этот эффект скачкообразного перехода от стабильного движения к мертвой пробке — один из примеров фазовых переходов. Оказалось, что в агентских системах такие явления встречаются сплошь и рядом, и условия, при которых происходит фазовый переход, отнюдь не тривиальны. Для того, чтобы можно было моделировать, необходимы соответствующие средства. Если уж я говорю, что это мультиагентские системы, значит агенты – объекты, а объекты между собой взаимодействуют. У нас взаимозависимости между переменными, описывающими каждого агента.

Следующий пример – глубинное обучение. Картинка взята из доклада представителя корпорации Google на конференции ICML 2012, где они произвели фурор тем, что смогли существенно поднять качество классификаций фотографий из базы Flickr путем применения сравнительно молодой парадигмы в машинном обучении — deep learning. В каком-то виде это реинкарнация нейронных сетей на новый лад. Традиционные нейронные сети успешно приказали долго жить. Тем не менее, они инспирировали в каком-то виде появление иного подхода. Глубинные сети, сети Больцмана, которые из себя представляют некую совокупность ограниченных машин Больцмана. По сути это слои взаимосвязанных между собой бинарных переменных. Эти переменные можно интерпретировать как скрытые переменные, которые при принятии решения каким-то образом настраиваются по наблюдаемым переменным. Но особенностью является то, что все скрытые переменные здесь между собой хитрым образом взаимозависимы. Чтобы такую сеть обучить и для того, чтобы в рамках такой сети принять решение, нам опять приходится применять методы, основанные на анализе объектов с взаимозависимыми переменными.
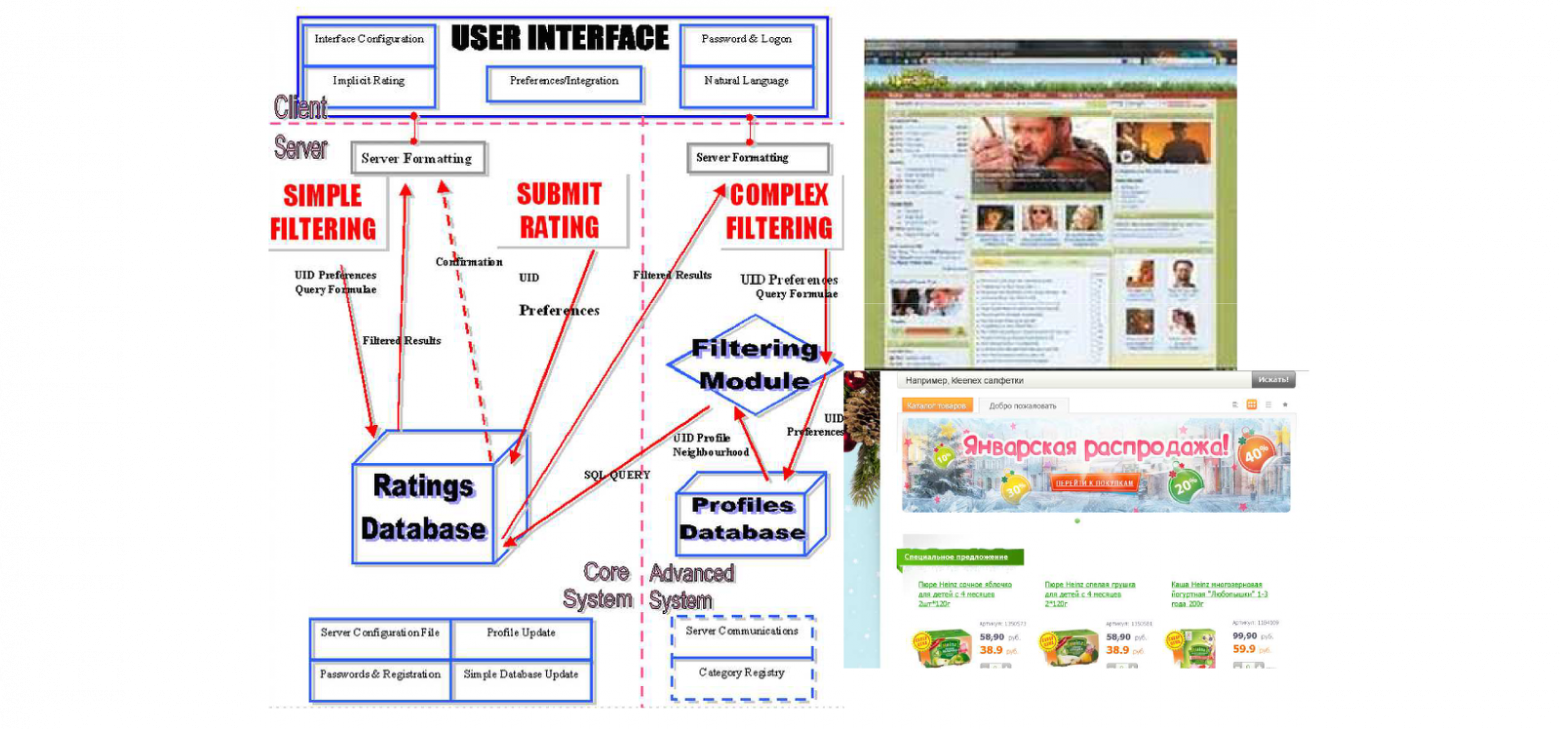
Наконец, последнее приложение из того, что мне в голову пришло – коллабративная фильтрация или рекомендательная система. Тоже сравнительно новое направление. Однако по понятным причинам оно набирает все большую популярность. Сейчас активно развиваются интернет-магазины, предоставляющие десятки и сотни тысяч наименований товаров, т.е. такое количество, которое ни один пользователь не в состоянии даже взглядом охватить. Ясно, что пользователь будет просматривать только те товары, которые ему предварительно каким-то образом отобрали из этого гигантского ассортимента. Соответственно, возникают задачи построения рекомендательной системы. Построить ее можно анализируя не только конкретного пользователя (какие товары он уже покупал, его анкетные данные, пол, возраст), но и поведение других пользователей, которые покупали похожие товары. Опять же возникают взаимозависимости между переменными.
Надеюсь, что мне удалось показать актуальность того, что действительно от классических постановок машинного обучения приходится отходить, и что мир на самом деле сложнее и интереснее. Приходится переходить к задачам, когда у нас есть объекты, у которых есть взаимозависимые скрытые компоненты. Как следствие, приходится моделировать сильно многомерное распределение, например, на скрытые компоненты. Тут возникает неприятность. Представим простейшую ситуацию. Скажем, тысяча объектов, у каждого из них скрытая переменная бинарна, может принимать значения 0/1. Если мы хотим задать совместное распределение, где все зависит от всего, значит, нам нужно формально задать тысячемерное распределение на бинарные переменные. Вопрос: сколько нам для этого потребуется параметров, чтобы такое распределение задать? Ответ: 21000 или приблизительно 10300. Для сравнения, количество атомов в наблюдаемой вселенной — 1080. Очевидно, что задать 10300 мы не можем, даже если объединим вычислительные мощности всего мира. Представим картинку 30x30, у которой каждый пиксель может принимать значение объект/фон. Распределение на множестве таких картинок мы не можем посчитать в принципе, так как распределение дискретно и требует 21000 параметров.
Что же делать? Первый вариант который приходит в голову, предположим, что каждый пиксель у нас распределен независимо от других. Тогда нам потребуется всего тысяча параметров, т.е. вероятность того, что каждый пиксель принимает значение, скажем, 1. Тогда -1 — это вероятность того, что он принял значение 0. Так работает стандартное машинное обучение. Одна маленькая проблема — все переменные стали независимы. Значит, ни одну из перечисленных задач мы таким образом решить не можем. Вопрос: как нам ограничится небольшим количеством параметров, но задать распределение, в котором все зависит от всего? И вот тут как раз на помощь приходит парадигма графических моделей, которая предполагает, что у нас совместное распределение может быть представлено в виде произведения некоторого количества факторов, определенных на пересекающихся подмножествах переменных. Для того, чтобы эти факторы задать, традиционно использовался неориентированный граф, который связывает какие-то объекты в выборке между собой, и система факторизации определяется максимальными кликами этого графа.
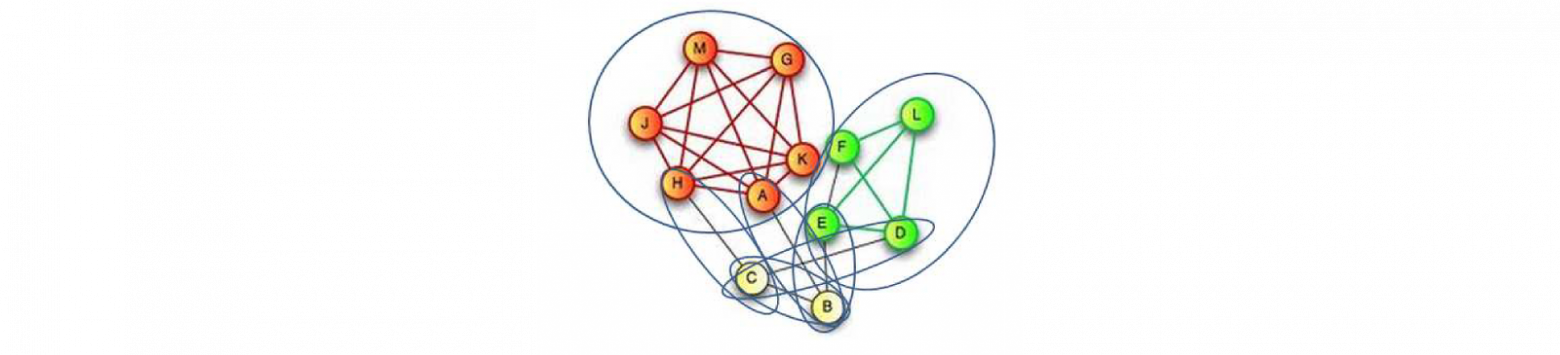
Эти клики очень небольшие, максимальные клики имеют размер 2. Это означает, что нам достаточно трех параметров, чтобы задать распределение на клики размера 2. Каждый такой фактор может быть задан небольшим количеством переменных, и, как следствие, поскольку таких факторов тоже не очень много, мы можем описать совместное распределение сравнительно небольшим количеством параметров. С другой стороны даже сравнительно простая система факторизации нам гарантированно дает ситуацию, когда у нас все переменные зависят от всех. Т.е. мы получили полную взаимозависимость, ограничившись некоторой системой факторизации. Система факторизации определяет условные независимости.
Какие же в рамках теории графических моделей возникают основные задачи? Аппарат был такой предложен в конце девяностых годов: совместное распределение моделировать в виде некоторой системы факторизации. Предположим, мы такую систему ввели. Тогда возвращаемся к задачам машинного обучения, которые в Байесовской формулировке предполагали, что у нас задано распределение на три группы величин: скрытые переменные Т, наблюдаемые переменные X и параметр решающего правила W. Оказалось, что в рамках графических моделей задачи очень похожи.
Оставшаяся часть доклада посвящена разбору задачи обучения с учителем. Посмотреть доклад целиком можно здесь.
Видеозапись доклада.
План доклада:
- Байесовские методы в машинном обучении.
- Задачи с взаимозависимыми скрытыми переменными.
- Вероятностные графические модели
- Метод опорных векторов и его обобщение для настройки параметров графических моделей.
Сама концепция машинного обучения довольно несложная – это, если говорить образно, поиск взаимосвязей в данных. Данные представляются в классической постановке набором объектов, взятых из одной и той же генеральной совокупности, у каждого объекта есть наблюдаемые переменные, есть скрытые переменные. Наблюдаемые переменные (дальше будем их обозначать X) часто называются признаками, соответственно, скрытые переменные (T) — это те, которые подлежат определению. Для того, чтобы эту взаимосвязь между наблюдаемыми и скрытыми переменными установить, предполагается, что у нас есть обучающая выборка, т.е. набор объектов, для которых известны и наблюдаемые и скрытые компоненты. Глядя на нее, мы пытаемся настроить некоторые решающие правила, которые нам позволят в дальнейшем, когда мы видим набор признаков, оценить скрытые компоненты. Процедура обучения приблизительно выглядит следующим образом: фиксируется множество допустимых решающих правил, которые как правило задаются с помощью весов (W), а дальше каким-то образом в ходе обучения эти веса настраиваются. Тут же с неизбежностью возникает проблема переобучения, если у нас слишком богатое семейство допустимых решающих правил, то в процессе обучения мы легко можем выйти на случай, когда для обучающей выборки мы прекрасно прогнозируем ее скрытую компоненту, а вот для новых объектов прогноз оказывается плохой. Исследователями в области машинного обучения было потрачено немало лет и усилий для того, чтобы эту проблему снять с повестки дня. В настоящее время, кажется, что худо-бедно это удалось.
Байесовская парадигма является подразделом машинного обучения, и в этом случае предполагается, что взаимосвязь между настраиваемыми параметрами W, наблюдаемыми переменными X и скрытыми переменными Т моделируется в виде некоторого совместного распределения, например, на все эти три группы переменных. Соответственно в классической постановке задач машинного обучения т.е., когда предполагается, что данные представляют из себя совокупность объектов, взятых из одной и той же генеральной совокупности независимых объектов, это совместное распределение можно представить вот в таком вот сравнительно простом виде:
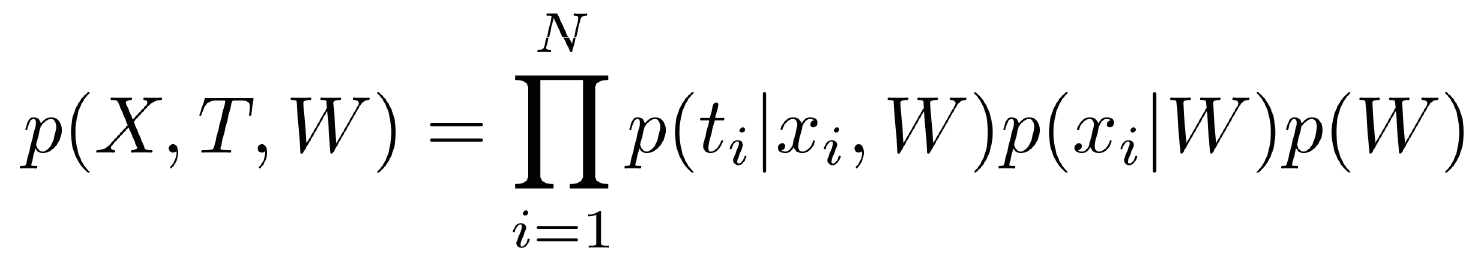
Первый множитель отвечает за распределение скрытой переменной при известных признаках и заданном решающем правиле. Второй множитель отвечает за распределение наблюдаемых переменных при заданном решающем правиле (так называемых дискриминативных моделях). Этот множитель нас не интересует, поскольку мы не моделируем распределение наблюдаемых переменных. Но более в общем случае так называемых генеративных моделей он имеет место быть. И, наконец, последний множитель, который неизбежно вытекает, если мы просто рассмотрим правило работы с вероятностями – это априорное распределение на веса W, т.е. на значения параметров решающего правила. И вот именно тот факт, что у нас появилась возможность задавать это априорное распределение, наверное, и явился ключевой причиной, почему Байесовские методы последние 10 лет переживает бум. Долгое время, до середины девяностых годов, Байесовский подход к теории вероятностей достаточно скептически воспринимался исследователями по той причине, что он предполагает, что мы каким-то образом должны задавать априорное распределение на параметры. И традиционный вопрос был – откуда его брать. Функция правдоподобия, понятно, определяется данными, а априорное распределение брать с потолка? Ясно что, если будем брать по-разному априорное распределение, будем получать в итоге разные результаты, применяя формулу Байеса. Поэтому долгое время Байесовский подход казался некоторой игрой ума. Тем не менее, примерно в середине девяностых годов пошел шквал работ, где доказывалось, что общие, стандартные методы машинного обучения можно существенно улучшить, если мы будем учитывать специфику решаемой задачи.
Оказалось, что специфика много где есть, вроде как все задачи сводятся к стандартным постановкам, но в большинстве случаев есть некоторая специфика, некоторые априорные предпочтения на ту или иную форму решающего правила. Т.е. фактически предпочтения на те или иные значения весов W. И тогда возник вопрос, как это можно объединить с качеством работы решающего правила на обучающей выборке? Традиционно процедура машинного обучения выглядит как минимизация ошибки на обучении, т.е. мы пытаемся построить решающее правило так, чтобы как можно точнее прогнозировать переменные Т для обучающей выборки, для которой они известны. Т.е. мы можем оценить качество. Это один показатель. Другой показатель заключается в том, что мы считаем, некоторые значения W более предпочтительными.
Как это все можно увязать в единых терминах? Оказалось, что в рамках Байесовской парадигмы это возможно. Качественное на обучении характеризуется функцией правдоподобия, которая есть вероятностный смысл, а предпочтение на параметры характеризуется априорным распределением. Соответственно, функция правдоподобия и априорное распределение отлично сочетаются в рамках формулы Байеса и приводят к апостериорным распределениям на значения параметров W, которые мы в ходе обучения настраиваем. Тем самым Байесовская парадигма дала возможность корректно в единых терминах скомбинировать как точность обучающей выборки, так и наши априорные предпочтения на значения весов, которые в очень многих прикладных задачах достаточно органично возникали, и, соответственно, введение этих априорных предпочтений позволило существенно поднять качество получаемых решающих правил. Кроме того, с конца девяностых и в нулевые годы появились более продвинутые средства, которые позволяют еще и априорное распределение некоторым хитрым образом параметризовать и настраивать по данным. Т.е. на кнопку нажал, и автоматически настроилось априорное распределение, наиболее подходящее для данной задачи, после чего пошла процедура машинного обучения.
Эти методы уже неплохо разработаны. Не будет сильным преувеличением сказать, что классическая постановка задачи машинного обучения решена. И как это часто бывает в жизни, как только мы закрыли классическую постановку, тут же оказалось, что нас больше интересуют неклассические постановки, которые оказались гораздо более богаты и интересны. Неклассическая постановка в даном случае — это ситуация, когда скрытые переменные объектов оказываются взаимозависимы. Т.е. мы не можем определить скрытую переменную каждого объекта, глядя только на признаки этого объекта, как предполагалось в традиционной задаче машинного обучения. Более того, она зависит не только и не столько от признаков других объектов, сколько от скрытых переменных других объектов. Соответственно, мы не можем определять скрытую переменную каждого объекта независимо, только в совокупности. Ниже я приведу большое количество примеров задач с взаимосвязанными скрытыми компонентами. Можно заметить, что эти взаимосвязи, т.е. осознание того факта, что скрытые переменные в нашей выборке взаимозависимы, открывает широчайшие возможности для дополнительной регуляризации задач. Т.е. в конечном итоге для дальнейшего поднятия точности решения.
Сегментация изображений

Первый наиболее классический пример — сегментация изображений. Это средство, которое решать такие задачи с взаимозависимыми скрытыми переменными, с него, собственно и начался бум графических моделей. Задача стала крайне востребована с развитием цифровых камер. Что это такое? Для каждого пикселя мы пытаемся поставить некоторую метку класса. В простейшем случае с бинарной сегментацией мы пытаемся отделись объект от фона. В более сложных случаях мы пытаемся для объектов еще и какую-то семантику привнести. В принципе, эту задачу можно рассматривать как стандартную задачу классификации. Каждый пиксель является объектом, каждый пиксель может принадлежать к одному из К классов, у каждого пикселя есть определенный набор признаков. В простейшем случае это цвет, можно снять текстурные признаки, какую-то контекстную информацию, но представляется достаточно очевидным, что в данном случае у нас есть некоторая специфика. Соседние пиксели скорее всего принадлежат к одному и тому же классу, просто потому что в задаче сегментации мы предполагаем, что у нас результатом сегментации будут некоторые компактные области. Как только мы попытаемся этот факт формализовать, у нас неизбежно вытекает, что мы не можем каждый пиксель классифицировать или сегментировать в отрыве от всего остального, мы можем сегментировать только всю картинку сразу. Вот простейшая задача, в которой появились взаимозависимости между скрытыми переменными.
Видеотрекинг

Следующая задача — видиотрекинг. Мы можем каждый кадр обрабатывать независимо, скажем, искать или идентифицировать пешеходов, идентифицировать пешеходов. Или делать трекинг мышей. Мыши сверху выглядят очень похоже, тречить их нужно так, чтобы еще каждая мышь идентифицировалась безошибочно. Попытки поставить цветные штрихи на шерсть жестко пресекаются биологами, которые утверждают, что мышь после этого будет в состоянии стресса. Соответственно, мыши все одинаковы, необходимо в каждый момент времени знать, где какая мышь у нас находится, чтобы анализировать их поведение. Ясно, что по отдельному кадру мы задачу решить не в состоянии. Нам необходимо учитывать соседние кадры, желательно в большом количестве. У нас снова возникают взаимозависимости между скрытыми переменными, где в качестве скрытой переменной выступает идентификатор мыши.
Анализ социальных сетей

Анализ социальных сетей сейчас – вполне очевидная задача. Каждого пользователя социальных сетей, конечно, можно анализировать независимо от других, но очевидно, что мы при этом потеряем значительный пласт информации. Например, мы пытаемся анализировать пользователей на предмет их оппозиционности действующему режиму. Если у меня стоит баннер «Навального в президенты!» или «Навального в мэры!», меня, конечно, можно идентифицировать как оппозиционера, но если я более осторожно к этому подхожу и подобные баннеры не вывешиваю, то определить, что я симпатизирую оппозиции, можно только проанализировав моих друзей менее осторожных, которые эти баннеры радостно развешивают. Если окажется, что я с большим количеством таких людей нахожусь в статусе друзей, то вероятность того, что я сам тоже симпатизирую этим течениям, несколько повышается. Ну а если уйти от подобной гбшной тематики, то, допустим, ту же задачу адресной рекламы можно решить гораздо лучше, если мы будем задействовать не только данные про конкретного пользователя (скажем, анкетные данные, которые он сообщил у себя на страничке), но и глядя на круг его друзей.
Вписывание 2D и 3D моделей

Следующая задача — это регистрация изображений для построения трехмерных моделей по изображению, вписывания изображения в двух- или трехмерную модель. Данная задача предполагает, что изображения подвергаются некоторым деформациям при регистрации. Мы, конечно, можем пытаться для каждого пикселя искать деформацию независимо от других, но ясно, что в этом случае никакой эластичной деформации мы не получим, результат будет довольно плачевный. Хотя формально мы каждый пиксель куда-то впишем, и погрешность для каждого пикселя будет минимальна. При этом все изображение у нас просто рассыплется, если каждый пиксель будет деформироваться независимо. В качестве одного из способов учета этих взаимозависимостей можно воспользоваться аппаратом графических моделей, который позволяет анализировать взаимозависимости скрытых переменных.
Декодирование зашумленных сообщений

Есть еще одна важная задача. О ней не так часто упоминают, но на самом деле она весьма актуальна и, скорее всего, в ближайшие годы актуальность будет только возрастать. Это декодирование зашумленных сообщений. Сейчас мы окружены мобильными устройствами. Передача данных с их помощью не слишком надежна, каналы жутко перегружены. Очевидно, что потребность в трафике превышает текущие возможности, поэтому естественным образом возникает задача составить такой протокол, который с одной стороны был бы помехоустойчив, а с другой обладал высокой пропускной способностью. Тут мы сталкиваемся с любопытным явлением. Еще с пятидесятых годов прошлого века, когда Клодом Шенноном была разработана теория информации, известно, что для каждого канала связи существует некая предельная пропускная способность при заданной интенсивности помех.
Была выведена теоритическая формула. Больше информации, чем предсказывает теорема Шеннона, передать по зашумленному каналу нельзя в принципе. Но оказывается, что по мере приближения к этому теоритическому пределу, т.е. чем более эффективно мы пытаемся информацию передавать, применяя некоторые хитрые схемы архивации и добавление контрольных битов, которые как раз направлены на исправление ошибок, тем сложнее у нас схема декодирования этого сообщения. Т.е. наиболее эффективные помехоустойчивые коды крайне сложны в декодировке. Там не существует простых формул декодирования. Соответственно, если мы достигаем предела Шеннона, сложность декодирования возрастает экспоненциально. Закодировать и передать сообщение мы можем, а расшифровать его уже не в состоянии. Оказалось, что современные коды, разработанные и стандартизованные в нулевые годы (их сейчас используют в в большинстве мобильных устройств), близки к этому теоретически возможному пределу, и для их декодировки используются так называемый алгоритм передачи сообщений, основанный на алгоритме распространения доверия, который появился в теории графических моделей, возникшей в попытке решить задачу с взаимосвязанными скрытыми переменными.
Имитационное моделирование

В конце девяностых также стала популярна задача, которую я условно назвал имитационным моделированием или моделированием агентских сред. Это попытка проанализировать поведение систем, состоящих из большого количества взаимодействующих агентов. Задача крайне интересная, строгих методов для ее решения не существует. Поэтому большинство этих задач решается с помощью симуляции методами Монте-Карло в различных модификациях. Простой пример – моделирование дорожного движения. В качестве агента выступают транспортные средства, ясно, что мы не можем моделировать поведение автомобилей вне контекста, так как все водители принимают решения, глядя на ближайших своих соседей по автотрассе. И оказалось, внесение в модель даже простейшего взаимодействия между автомобилистами, позволило получить потрясающий результат. Во-первых, было установлено сначала в теории, а потом и на практике, что есть некоторый критический предел интенсивности потока. Если поток превышает этот предел, то он становится метастабильным, т.е. неустойчивым. Малейшее отклонение от нормы (допустим, один из водителей чуть резче затормозил и сразу поехал дальше) приводит к тому, что тут же вырастают пробки на десятки километров. Это означает, что когда транспортный канал перегружен, он еще может функционировать без пробок, но пробка может возникнуть практически на ровном месте.
Сначала это получили в теории, потом убедились, что на практике действительно такое бывает. Действительно для каждой трассы, в зависимости от ее развязок, существует некая предельная пропускная способность, при которой поток еще движется стабильно. Этот эффект скачкообразного перехода от стабильного движения к мертвой пробке — один из примеров фазовых переходов. Оказалось, что в агентских системах такие явления встречаются сплошь и рядом, и условия, при которых происходит фазовый переход, отнюдь не тривиальны. Для того, чтобы можно было моделировать, необходимы соответствующие средства. Если уж я говорю, что это мультиагентские системы, значит агенты – объекты, а объекты между собой взаимодействуют. У нас взаимозависимости между переменными, описывающими каждого агента.
Глубинное обучение

Следующий пример – глубинное обучение. Картинка взята из доклада представителя корпорации Google на конференции ICML 2012, где они произвели фурор тем, что смогли существенно поднять качество классификаций фотографий из базы Flickr путем применения сравнительно молодой парадигмы в машинном обучении — deep learning. В каком-то виде это реинкарнация нейронных сетей на новый лад. Традиционные нейронные сети успешно приказали долго жить. Тем не менее, они инспирировали в каком-то виде появление иного подхода. Глубинные сети, сети Больцмана, которые из себя представляют некую совокупность ограниченных машин Больцмана. По сути это слои взаимосвязанных между собой бинарных переменных. Эти переменные можно интерпретировать как скрытые переменные, которые при принятии решения каким-то образом настраиваются по наблюдаемым переменным. Но особенностью является то, что все скрытые переменные здесь между собой хитрым образом взаимозависимы. Чтобы такую сеть обучить и для того, чтобы в рамках такой сети принять решение, нам опять приходится применять методы, основанные на анализе объектов с взаимозависимыми переменными.
Коллаборативная фильтрация

Наконец, последнее приложение из того, что мне в голову пришло – коллабративная фильтрация или рекомендательная система. Тоже сравнительно новое направление. Однако по понятным причинам оно набирает все большую популярность. Сейчас активно развиваются интернет-магазины, предоставляющие десятки и сотни тысяч наименований товаров, т.е. такое количество, которое ни один пользователь не в состоянии даже взглядом охватить. Ясно, что пользователь будет просматривать только те товары, которые ему предварительно каким-то образом отобрали из этого гигантского ассортимента. Соответственно, возникают задачи построения рекомендательной системы. Построить ее можно анализируя не только конкретного пользователя (какие товары он уже покупал, его анкетные данные, пол, возраст), но и поведение других пользователей, которые покупали похожие товары. Опять же возникают взаимозависимости между переменными.
Графические модели
Надеюсь, что мне удалось показать актуальность того, что действительно от классических постановок машинного обучения приходится отходить, и что мир на самом деле сложнее и интереснее. Приходится переходить к задачам, когда у нас есть объекты, у которых есть взаимозависимые скрытые компоненты. Как следствие, приходится моделировать сильно многомерное распределение, например, на скрытые компоненты. Тут возникает неприятность. Представим простейшую ситуацию. Скажем, тысяча объектов, у каждого из них скрытая переменная бинарна, может принимать значения 0/1. Если мы хотим задать совместное распределение, где все зависит от всего, значит, нам нужно формально задать тысячемерное распределение на бинарные переменные. Вопрос: сколько нам для этого потребуется параметров, чтобы такое распределение задать? Ответ: 21000 или приблизительно 10300. Для сравнения, количество атомов в наблюдаемой вселенной — 1080. Очевидно, что задать 10300 мы не можем, даже если объединим вычислительные мощности всего мира. Представим картинку 30x30, у которой каждый пиксель может принимать значение объект/фон. Распределение на множестве таких картинок мы не можем посчитать в принципе, так как распределение дискретно и требует 21000 параметров.
Что же делать? Первый вариант который приходит в голову, предположим, что каждый пиксель у нас распределен независимо от других. Тогда нам потребуется всего тысяча параметров, т.е. вероятность того, что каждый пиксель принимает значение, скажем, 1. Тогда -1 — это вероятность того, что он принял значение 0. Так работает стандартное машинное обучение. Одна маленькая проблема — все переменные стали независимы. Значит, ни одну из перечисленных задач мы таким образом решить не можем. Вопрос: как нам ограничится небольшим количеством параметров, но задать распределение, в котором все зависит от всего? И вот тут как раз на помощь приходит парадигма графических моделей, которая предполагает, что у нас совместное распределение может быть представлено в виде произведения некоторого количества факторов, определенных на пересекающихся подмножествах переменных. Для того, чтобы эти факторы задать, традиционно использовался неориентированный граф, который связывает какие-то объекты в выборке между собой, и система факторизации определяется максимальными кликами этого графа.

Эти клики очень небольшие, максимальные клики имеют размер 2. Это означает, что нам достаточно трех параметров, чтобы задать распределение на клики размера 2. Каждый такой фактор может быть задан небольшим количеством переменных, и, как следствие, поскольку таких факторов тоже не очень много, мы можем описать совместное распределение сравнительно небольшим количеством параметров. С другой стороны даже сравнительно простая система факторизации нам гарантированно дает ситуацию, когда у нас все переменные зависят от всех. Т.е. мы получили полную взаимозависимость, ограничившись некоторой системой факторизации. Система факторизации определяет условные независимости.
Основные задачи
Какие же в рамках теории графических моделей возникают основные задачи? Аппарат был такой предложен в конце девяностых годов: совместное распределение моделировать в виде некоторой системы факторизации. Предположим, мы такую систему ввели. Тогда возвращаемся к задачам машинного обучения, которые в Байесовской формулировке предполагали, что у нас задано распределение на три группы величин: скрытые переменные Т, наблюдаемые переменные X и параметр решающего правила W. Оказалось, что в рамках графических моделей задачи очень похожи.
- Принятие решения. Задано решающее правило W, есть выборка, у которой мы видим у наблюдаемые переменные. Задача — оценить скрытые переменные. Применительно к стандартным задачам машинного обучения задача решается легко и даже никем не рассматривается. В графических моделях задача стала уже существенно нетривиальной и далеко не всегда разрешимой.
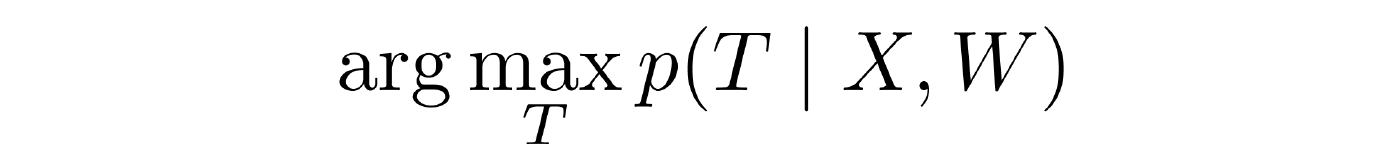
- Определение нормировочной константы Z. Вычислять ее не всегда легко.
- Обучение с учителем. Дана обучающая выборка, в которой мы знаем не только наблюдаемые переменные, но и скрытые. Это некоторая совокупность взаимосвязанных объектов. Требуется найти вектор W, который обращает в максимум совместное распределение.
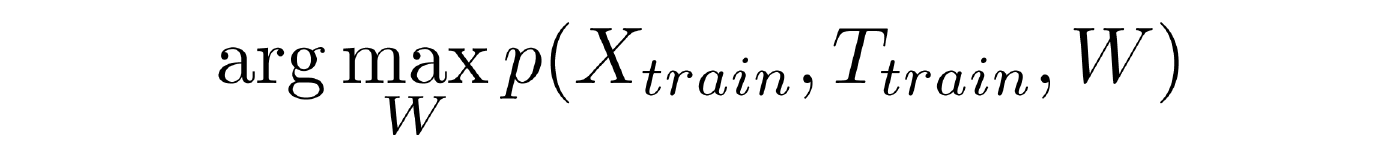
- Обучение без учителя. Дана выборка, но в ней мы знаем только наблюдаемые компоненты, скрытые не знаем. Мы хотим настроить наше решающее правило. Задача оказывается крайне сложной, потому что конфигураций Т довольно много.
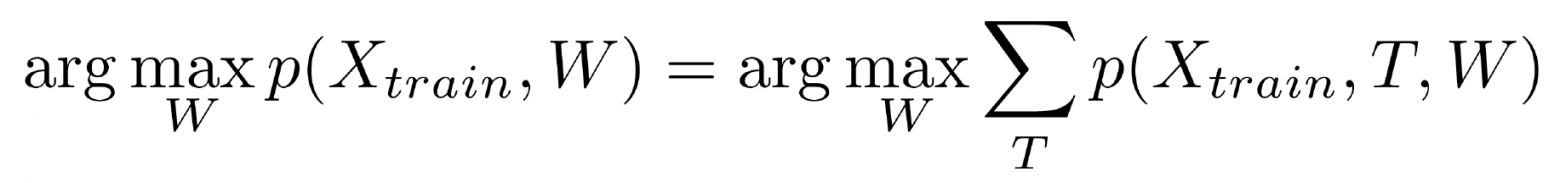
- Маргинальные распределения. Дана выборка, известны наблюдаемые компоненты Х, известно решающее правило W, но мы хотим найти не наиболее вероятную конфигурацию всех скрытых переменных выборки, а распределение на скрытые переменные для какого-то одного объекта. Задача часто актуальна в приложениях. Решается нетривиально.
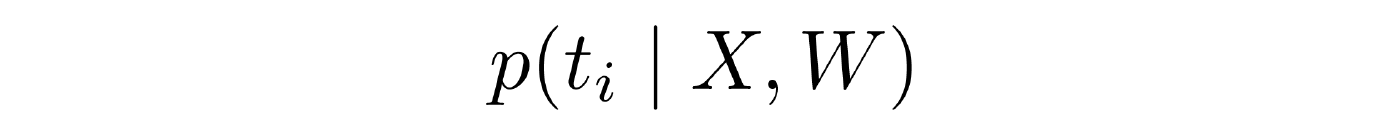
Оставшаяся часть доклада посвящена разбору задачи обучения с учителем. Посмотреть доклад целиком можно здесь.
