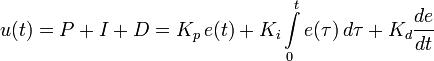Продолжая тему
распознавания голоса, хочу поделится своей старой дипломной работой, на которую одно время возлагал надежды по доведению до коммерческого продукта, но потом оставил этот проект, выложив его в сеть на радость другим студентам. Хотя возможно эта тема будет интересна не только в академическом ключе, а и для общего развития.
Тема моей дипломной работы была «Разработка подсистемы САПР защиты от несанкционированного доступа на основе нейросетевого анализа спектральных характеристик голоса». В самом дипломе конечно много воды вроде ТБ, экономики и прочего, но есть и математическая и практическая часть, а также анализ существующих аналогичных решений. В конце выложу программу и сам диплом, возможно еще кому-то пригодится.
Итак, зачем вообще это нужно?
Основным способом персонификации пользователя является указание его сетевого имени и пароля. Опасности, связанные с использованием пароля, хорошо известны: пароли забывают, хранят в неподходящем месте, наконец, их могут просто украсть. Некоторые пользователи записывают пароль на бумаге и держат эти записи рядом со своими рабочими станциями. Как сообщают группы информационных технологий многих компаний, большая часть звонков в службу поддержки связана с забытыми или утратившими силу паролями.
Метод работы существующих систем.
Большинство биометрических систем безопасности функционируют следующим образом: в базе данных системы хранится цифровой отпечаток пальца, радужной оболочки глаза или голоса. Человек, собирающийся получить доступ к компьютерной сети, с помощью микрофона, сканера отпечатков пальцев или других устройств вводит информацию о себе в систему. Поступившие данные сравниваются с образцом, хранимым в базе данных.
При распознавании образца проводится процесс, первым шагом которого является первоначальное трансформирование вводимой информации для сокращения обрабатываемого объема так, чтобы ее можно было бы подвергнуть анализу. Следующим этапом является спектральное представление речи, получившееся путем преобразования Фурье. Спектральное представление достигнуто путем использования широко-частотного анализа записи.
Хотя спектральное представление речи очень полезно, необходимо помнить, что изучаемый сигнал весьма разнообразен.
Разнообразие возникает по многим причинам, включая:
— различия человеческих голосов;
— уровень речи говорящего;
— вариации в произношении;
— нормальное варьирование движения артикуляторов (языка, губ, челюсти, нёба).
Затем определяются конечные выходные параметры для варьирования голоса и производится нормализация для составления шкалы параметров, а также для определения ситуационного уровня речи. Вышеописанные измененные параметры используются затем для создания шаблона. Шаблон включается в словарь, который характеризует произнесение звуков при передаче информации говорящим, использующим эту систему. Далее в процессе распознавания новых речевых образцов (уже подвергшихся нормализации и получивших свои параметры), эти образцы сравниваются с шаблонами, уже имеющимися в базе, используя динамичное искажение и похожие метрические измерения.
Возможность использования нейросетей для построения системы распознавания речи
Любой речевой сигнал можно представить как вектор в каком-либо параметрическом пространстве, затем этот вектор может быть запомнен в нейросети. Одна из моделей нейросети, обучающаяся без учителя – это самоорганизующаяся карта признаков Кохонена. В ней для множества входных сигналов формируется нейронные ансамбли, представляющие эти сигналы. Этот алгоритм обладает способностью к статистическому усреднению, т.е. решается проблема с вариативностью речи. Как и многие другие нейросетевые алгоритмы, он осуществляет параллельную обработку информации, т.е. одновременно работают все нейроны. Тем самым решается проблема со скоростью распознавания – обычно время работы нейросети составляет несколько итераций.
Практическая работа используемого алгоритма
Процесс сравнивания образцов состоит из следующих стадий:
— фильтрация шумов;
— спектральное преобразование сигнала;
— постфильтрация спектра;
— лифтеринг;
— наложение окна Кайзера;
— сравнение.
Фильтрация шумов
Звук, образованный колебаниями всего диапазона частот, подобный тому, спектр которого показан на рисунке, называется шумом.

Для того чтобы получить четкие спектральные характеристики звука их нужно отчистить от лишних шумов.
Входной дискретный звуковой сигнал обрабатывается фильтрами, для того чтобы избавится от помех возникающих при записи по формуле.

где Xi – набор дискретных значений звукового сигнала.
После обработки в сигнале ищется начало и конец записи, а так как шумы уже отфильтрованы, то начало фрагмента будет характеризоваться всплеском сигнала, если искать с Х0. Соответственно если искать с Хn вниз, то всплеск будет характеризовать конец фрагмента. Таким образом получим начала и конца фрагмента в массиве дискретных значений сигнала. В нематематическом виде это означает, что мы нашли слово сказанное пользователем в микрофон, которое нужно усреднить с другими характеристиками голоса.
Помимо высоты тона человек ощущает и другую характеристику звука — громкость. Физические величины, наиболее точно соответствующие громкости, — это шоковое давление (для звуков в воздухе) и амплитуда (для цифрового или электронного представления звука).
Если говорить об оцифрованном сигнале, то амплитуда — это значение выборки. Анализируя миллионы дискретных значений уровня одного и того же звука, можно сказать о пиковой амплитуде, то есть об абсолютной величине максимального из полученных дискретных значений уровня звука. Чтобы избежать искажения, вызванного искажением ограничения сигнала при цифровой записи звука (данное искажение возникает в том случае, если величина пиковой амплитуды выходит за границы, определяемые форматом хранения данных), необходимо обратить внимание на величину пиковой амплитуды. При этом нужно сохранять отношение сигнал/шум на максимально достижимом уровне.
Основной причиной разной громкости звуков является различное давление, оказываемое ими на уши. Можно сказать, что волны давления обладают различными уровнями мощности. Волны, несущие большую мощность, с большей силой оказывают воздействие на механизм ушей. Электрические сигналы, идущие по проводам, также передают мощность. По проводам звук обычно передается в виде переменного напряжения, и мгновенная мощность этого звука пропорциональна квадрату напряжения. Чтобы определить полную мощность за период времени, необходимо просуммировать все значения моментальной мощности за этот период.
На языке математики это описывается интегралом

, где
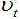
— это напряжение в заданный момент времени.
Поскольку вы используете звук, представленный дискретными значениями, вам не понадобится брать интеграл. Достаточно просто сложить квадраты отсчетов. Среднее значение квадратов дискретных значений пропорционально средней мощности.
Так как моментальная мощность зависит от квадрата моментальной амплитуды, имеет смысл аналогичным образом подобрать похожее соотношение, связывающее среднюю амплитуду и среднюю мощность. Способ, которым это можно сделать, заключается в определении средней амплитуды (СКЗ). Вместо того, чтобы вычислять среднее значение непосредственно амплитуды, мы сначала возводим в квадрат полученные значения, вычисляем среднее значение получившегося множества, а затем извлекаем из него корень. Метод СКЗ применяется в том случае, когда необходимо вычислить среднее для быстро меняющейся величины. Алгебраически это выражается следующим ооразом: пусть у нас N значений и х(i) это амплитуда i-ого дискретного значения. Тогда СКЗ амплитуды =
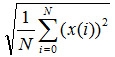
Мощность пропорциональна возведенной в квадрат величине дискретного значения. Это означает, что для перехода к реальной мощности, эту величину необходимо умножить на некоторый коэффициент. Для этого не требуются точные данные электрической мощности, так что, на самом деле, нас не интересуют точные числа, скорее относительная мощность.
Относительная мощность измеряется в белах, а чаще в децибелах (дБ, децибел, это одна десятая бела). Чтобы сравнить два звука, берется отношение их мощности. Десятичный логарифм этого отношения и есть различие в белах; если множить получившееся число на десять, то получится значение в децибелах. Например, если мощность одного сигнала превосходит мощность другого в два раза, то первый сигнал будет громче на 10lоg10(2) = 3,01 дБ.
Спектральное преобразование сигнала
Поскольку любой звук раскладывается на синусоидальные волны, мы можем построить частотный спектр звука. Спектр частот звуковой волны представляет собой график зависимости амплитуды от частоты.
Фазовые изменения часто происходят по причине временных задержек. Например, каждый цикл сигнала в 1000 Гц занимает 1/1000 секунды. Если задержать сигнал на 1/2000 секунды (полупериод), то получится 180-градусный сдвиг но фазе. Заметим, что этот эффект опирается на зависимость между частотой и временной задержкой. Если сигнал в 250 Гц задержать на те же самые 1/2000 секунды, то будет реализован 45-градусный сдвиг по фазе.
Если сложить вместе две синусоидальные волны одинаковой частоты, то получится новая синусоидальная волна той же частоты. Это будет верно даже в том случае, если два исходных сигнала имеют разные амплитуды и фазы. Например, Asin(2 Pi ft) и Bcos(2 Pi ft) две синусоиды с разными амплитудами и фазами, но I c одинаковой частотой.
Для измерения амплитуды одной частоты нужно умножить имеющийся сигнал на синусоиду той же частоты и сложить полученные отсчеты.
Чтобы записать это в символьном виде, предположим, что отсчеты имеют значения s0, s1, …, st, …. Переменная t представляет собой номер отсчета (который заменяет значение времени). Измеряется амплитуду частоты f в первом приближении, при вычислении следующей суммы:
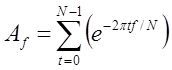
Значения t и f не соответствуют в точности времени и частоте. Более того, f – целое число, а реальная исследуемая частота – это частота дискретизации, умноженная на f/N. Подобным образом, t — это целочисленный номер отсчета. Кроме того, суммирование дает не непосредственное значение амплитуды, а всего лишь число, пропорциональное амплитуде.
Если повторить эти вычисления для различных значений f, то можно измерить амплитуду всех частот в сигнале. Для любого целого f меньшего N легко определяется значение Аf, представляющее амплитуду соответствующей частоты как долю от общего сигнала. Эти значения могут быть вычислены по той же формуле:
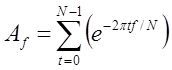
Если мы знаем значения Af мы можем восстановить отсчеты. Для восстановления сигнала необходимо сложить все значения для разных частот. Чтобы осуществлять точное обратное преобразование Фурье, помимо амплитуды и частоты необходимо измерять фазу каждой частоты.
Для этого нужны комплексные числа. Можно изменить описанный ранее метод вычислений так, что он будет давать двумерный результат. Простое коми1 лексное число – это двумерное значение, поэтому оно одновременно но представляет и амплитуду, и фазу.
При таком подходе фазовая часть вычисляется неявно. Вместо амплитуды и фазы измеряется две амплитуды, соответствующие разным фазам. Одна из этих фаз представляется косинусом (соs()), другая синусом sin()).
Используя комплексные числа, можно проводить измерения одновременно, умножая синусную часть на -i.

Каждое значение Af теперь представляется комплексным числом; действительная и мнимая части задают амплитуду двух синусоидальных волн с разным фазами.
Основная идея быстрого преобразования Фурье заключается в том, что каждую вторую выборку можно использовать для получения половинного спектра. Формально это означает, что формула дискретного преобразования Фурье может быть представлена в виде двух сумм. Первая содержит все четные компоненты оригинала, вторая — все нечетные
 Фильтрация спектра.
Фильтрация спектра.
Получив спектральное представление сигнала его требуется отчистить от шумов. Человеческий голос обладает известными характеристиками, и поэтому те области которые не могут являются характеристиками голоса нужно погасить. Для этого применим функцию, которая получила название «окно Кайзера»


После фильтрации спектра наложим окно Ханнинга
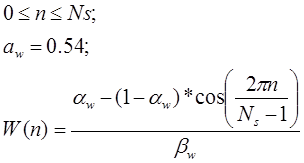 Сравнение с эталонными образцами в базе
Сравнение с эталонными образцами в базе
Основным параметром, используемым для идентификации, является мера сходства двух звуковых фрагментов. Для ее вычисления необходимо сравнить спектрограммы этих фрагментов. При этом сначала сравниваются спектры, полученные в отдельном окне, а затем вычисленные значения усредняются.
Для сравнения двух фрагментов использовался следующий подход:
Предположим что X[1..N] и Y[1..N] массивы чисел, одинакового размера N, содержащие значения спектральной мощности первого и второго фрагментов соответственно. Тогда мера сходства между ними вычисляется по следующей формуле:
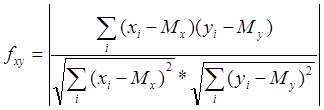
где Mx и My математические ожидания для массивов X[] и Y[] соответственно, вычисляющиеся по следующей формуле:

Данный способ вычисления меры сходства двух фрагментов представленных в виде спектра является самым оптимальным для задачи идентификации человека по его голосу.
Нейросетевое сравнение на основе простых персептронов
Несмотря на большое разнообразие вариантов нейронных сетей, все они имеют общие черты. Так, все они, так же, как и мозг человека, состоят из большого числа связанных между собой однотипных элементов – нейронов, которые имитируют нейроны головного мозга. На рисунке показана схема нейрона.

Из рисунка видно, что искусственный нейрон, так же, как и живой, состоит из синапсов, связывающих входы нейрона с ядром; ядра нейрона, которое осуществляет обработку входных сигналов и аксона, который связывает нейрон с нейронами следующего слоя. Каждый синапс имеет вес, который определяет, насколько соответствующий вход нейрона влияет на его состояние. Состояние нейрона определяется по формуле
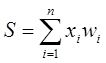
где n – число входов нейрона, xi – значение i-го входа нейрона, wi – вес i-го синапса
Затем определяется значение аксона нейрона по формуле: Y = f(S) где f – некоторая функция, которая называется активационной. Наиболее часто в качестве активационной функции используется так называемый сигмоид, который имеет следующий вид:

Основное достоинство этой функции в том, что она дифференцируема на всей оси абсцисс и имеет очень простую производную:

При уменьшении параметра α сигмоид становится более пологим, вырождаясь в горизонтальную линию на уровне 0,5 при α=0. При увеличении a сигмоид все больше приближается к функции единичного скачка.
Обучение сети
Для автоматического функционирования системы был выбран метод обучения сети без учителя. Обучение без учителя является намного более правдоподобной моделью обучения в биологической системе. Развитая Кохоненом и многими другими, она не нуждается в целевом векторе для выходов и, следовательно, не требует сравнения с предопределенными идеальными ответами. Обучающее множество состоит лишь из входных векторов. Обучающий алгоритм подстраивает веса сети так, чтобы получались согласованные выходные векторы, т. е. чтобы предъявление достаточно близких входных векторов давало одинаковые выходы.
Персептрон обучают, подавая множество образов по одному на его вход и подстраивая веса до тех пор, пока для всех образов не будет достигнут требуемый выход. Допустим, что входные образы нанесены на демонстрационные карты. Каждая карта разбита на квадраты и от каждого квадрата на персептрон подается вход. Если в квадрате имеется линия, то от него подается единица, в противном случае ноль. Множество квадратов на карте задает, таким образом, множество нулей и единиц, которое и подается на входы персептрона. Цель состоит в том, чтобы научить персептрон включать индикатор при подаче на него множества входов, задающих нечетное число, и не включать в случае четного.
Для обучения сети образ X подается на вход и вычисляется выход У. Если У правилен, то ничего не меняется. Однако если выход неправилен, то веса, присоединенные к входам, усиливающим ошибочный результат, модифицируются, чтобы уменьшить ошибку.
Информативность различных частей спектра неодинакова: в низкочастотной области содержится больше информации, чем в высокочастотной. Поэтому для предотвращения излишнего расходования входов нейросети необходимо уменьшить число элементов, получающих информацию с высокочастотной области, или, что тоже самое, сжать высокочастотную область спектра в пространстве частот.
Наиболее распространенный метод — логарифмическое сжатие
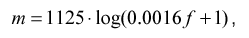
где
f — частота в спектре Гц,
m — частота в новом сжатом частотном пространстве
Такое преобразование имеет смысл только если число элементов на входе нейросети NI меньше числа элементов спектра NS.
После нормирования и сжатия спектр накладывается на вход нейросети. Вход нейросети — это линейно упорядоченный массив элементов, которым присваиваются уровни соответствующих частот в спектре. Эти элементы не выполняют никаких решающих функций, а только передают сигналы дальше в нейросеть. Выбор числа входов — сложная задача, потому что при малом размере входного вектора возможна потеря важной для распознавания информации, а при большом существенно повышается сложность вычислений ( при моделировании на PC, в реальных нейросетях это неверно, т.к. все элементы работают параллельно ).
При большой разрешающей способности (числе) входов возможно выделение гармонической структуры речи и как следствие определение высоты голоса. При малой разрешающей способности (числе) входов возможно только определение формантной структуры.
Как показало дальнейшее исследование этой проблемы, для распознавания уже достаточно только информации о формантной структуре. Фактически, человек одинаково распознает нормальную голосовую речь и шепот, хотя в последнем отсутствует голосовой источник. Голосовой источник дает дополнительную информацию в виде интонации (высоты тона на протяжении высказывания ), и эта информация очень важна на высших уровнях обработки речи. Но в первом приближении можно ограничиться только получением формантной структуры, и для этого с учетом сжатия неинформативной части спектра достаточное число входов выбрано в пределах 50~100.
Наложение спектра на каждый входной элемент происходит путем усреднения данных из некоторой окрестности, центром которой является проекция положения этого элемента в векторе входов на вектор спектра. Радиус окрестности выбирается таким, чтобы окрестности соседних элементов перекрывались. Этот прием часто используется при растяжении векторов, предотвращая выпадение данных.
Тестирование алгоритма
Тестирование производилось с 8 пользователями. Каждый голос сначала сравнивался с эталонным, то есть голосом разработчика, а потом между собой, для того что бы выяснить как поведет себя система на однотипных голосах.


 Листая страницы хаба «Алгоритмы», наткнулся на
Листая страницы хаба «Алгоритмы», наткнулся на 

 , где
, где 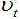 — это напряжение в заданный момент времени.
— это напряжение в заданный момент времени.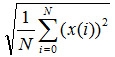
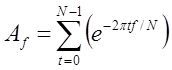




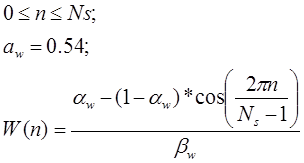
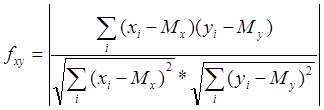




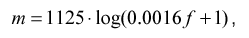
 Как
Как 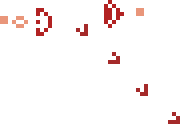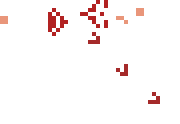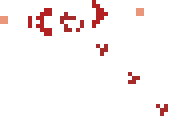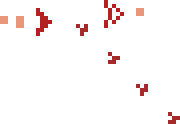 Обновляя недавно дизайн своего хомяка, подумал – а не сделать ли мне какую-нибудь необычную страницу с 404-й ошибкой? Поскольку в детстве я был впечатлен
Обновляя недавно дизайн своего хомяка, подумал – а не сделать ли мне какую-нибудь необычную страницу с 404-й ошибкой? Поскольку в детстве я был впечатлен