Comments 56
Недавно для диплома впервые написал Грэхема, был счастлив по самое «не хочу»: Джарвиса — самый наивный алгоритм, который только можно представить.
А насчёт выбора для использования — вообще без вариантов. Для общего набора Грэхем c O(NlogN) уделывает весьма специфичный квадратный алгоритм.
А насчёт выбора для использования — вообще без вариантов. Для общего набора Грэхем c O(NlogN) уделывает весьма специфичный квадратный алгоритм.
кажется очевидным, что минимальная оболочка просто обязана быть выпуклой
С чего бы это?
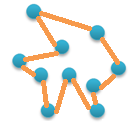
Эта оболочка не минимальна, её можно укоротить.
Она не минимальная. Соедините самую левую точку с самой верхней напрямую — уменьшите периметр, ибо длина одной стороны треугольника в любом случае не больше суммы длин двух других сторон.
В статье минимальная оболочка определена как оболочка с наименьшим периметром. На этой картинке явно периметр можно уменьшить, убрав впадины.
Выпуклость минимальной оболочки — прямое следствие из неравенства треугольника
Интересно, познавательно и понятно изложенно. Спасибо! Буду ждать новых постов :)
Спасибо, картинки крутые, сразу понятна суть алгоритма.
Что-то подобное в школе писал, только никаких алгоритмов не знал, сам придумал. Кажется я брал все пары точек, строил уравнение прямой через них и подставлял в уравнение координаты оставшихся точек. Если все получившиеся выражения имели одинаковый знак, то строил отрезок.
Что-то подобное в школе писал, только никаких алгоритмов не знал, сам придумал. Кажется я брал все пары точек, строил уравнение прямой через них и подставлял в уравнение координаты оставшихся точек. Если все получившиеся выражения имели одинаковый знак, то строил отрезок.
Я наверное Джарвис, потомучто именно этот алгоритм сразу пришел в голову глядя на вторую картинку из трех обрисованых множеств
Есть алгоритм пострения выпуклой оболочки методом «разделяй и властвуй». Тоже O(n log n), момедленнее гэхема на практике, но красиво!
moais.imag.fr/membres/denis.trystram/SupportsDeCours/convexHull.pdf
moais.imag.fr/membres/denis.trystram/SupportsDeCours/convexHull.pdf
там на самом деле минимум 3 подхода разделяй и властвуй. а к ним еще неплохо рассказать алгоритм построения опорной прямой. а если писать все методы, то надо экла-туссена еще расписать к примеру. но это уже получится листов 10-15 формата A4, с учетом того,, как подробно расписал их автор.
а в дополнение к этим 2 достаточно известным яростро напрашивается алгоритм Чана, который использует грехэма и джарвиса.
а в дополнение к этим 2 достаточно известным яростро напрашивается алгоритм Чана, который использует грехэма и джарвиса.
а вообще, отлично, очень клевые картинки, все смотрится. заменить питон на псевдокод и можно в простой школе как материал давать. рад бы был если автор так же что-нить более сложное и интересное расписал.
Добавлю, что ассимптотика у алгоритма Чана O(n log h), где h — количество точек в выпуклой оболочке.
Он интересен в том смысле, что похожим подходом можно трехмерную выпуклую оболочку строить.
Спасибо за ссылку, почитаю… На самом деле на википедии есть описания многих алгоритмов, осталось найти время их поизучать: Выпуклая оболочка, Convex_hull и Convex_hull_algorithms
кажется очевидным, что минимальная оболочка просто обязана быть выпуклой
Это элементарно доказывается с помощью свойства |AB| + |BC| >= |AC| (правило треугольника) и верно, кстати говоря, для любого нормированного пространства, а не только для плоскости.
Извиняюсь, в нормированном линейном пространстве.
Ага, неравенство треугольника я и имел в виду, когда писал про «очевидность» выпуклости. Думаю, что при строгом доказательстве для произвольных кривых возникнут некоторые трудности, нет? Для ломаных линий (т.е. для многоугольников, в контексте рассматриваемой темы) это не проблема, согласен…
Единственная трудность — придумать, куда воткнуть интеграл или предел.
А дальше — то же самое неравенство треугольника.
А дальше — то же самое неравенство треугольника.
Произвольных множеств точек, вы хотели сказать? Если множество конечно, то это все еще ломаная, если же бесконечно, но вложено в ограниченное подмножество плоскости, то тут веселее, понадобится предельные переход. Однако, если бесконечное множество точек на плоскости вложено в некоторое ограниченное ее подмножество, то никаких проблем нет: алгоритм точно такой же: индуктивное применение неравенства треугольника. Только индукция тут трансфинитная.
Можно проще и без пределов. Легко доказать что для любой не выпуклой оболочки существует выпуклая оболочка меньшей длины содержащая данную. Алгоритм построения этой оболочки — соединяем ближайшие две точки в которых нарушается выпуклость (касательная пересекает оболочку) прямой. Из того факта, что минимальное расстояние между двумя точками — отрезок прямой следует, что построенная оболочка имеет длину меньше чем данная.
Конечно, если доказывать, что минимальное расстояние между двумя точками — отрезок прямой соединяющей эти две точки (известная теорема) то без предела не обойтись, так как само понятие длины кривой содержит в себе предел.
Конечно, если доказывать, что минимальное расстояние между двумя точками — отрезок прямой соединяющей эти две точки (известная теорема) то без предела не обойтись, так как само понятие длины кривой содержит в себе предел.
Я в бытность свою школнегом, придумал алгоритм построения выпуклой оболочки, а какой то Джарвис его, оказывается, присвоил
Приятно видеть подобные посты, пишите почаще
Приятно видеть подобные посты, пишите почаще
А можно пару примеров реального практического применения? В смысле где это требуется?
Ну я вот сейчас пишу бота для старкрафта. Там надо иметь общее представление о своей территории и о территории противника и ограничить снаружи, то есть нарисовать огибающую линию.
Подобный алгоритм применяется для того чтобы запихать все свои здания в некоторый регион и наречь его потом «базой». Здания — это по сути точки на плоскости. Остальное думаю понятно.
Подобный алгоритм применяется для того чтобы запихать все свои здания в некоторый регион и наречь его потом «базой». Здания — это по сути точки на плоскости. Остальное думаю понятно.
Я хочу заметить что с машиной времени можно решать любую задачу намного легче: считываем данные, считываем из будущего ответ Х, через минуту начинаем проверять этот Х, если он не подходит (можно убедиться в теории и за миллиард лет, но особенно хорошо алгоритм работает с задачами из класса NP, где ответ проверяется быстро), то отправляем в прошлое Х+1, если же подходит отправляем Х. Так как отправленное число должно совпасть с полученным, Х гарантированно будет правильным ответом на задачу.
Спасибо, интересно!
Не вижу больше ни одной статьи, кроме этой, с тегом «вычислительная геометрия».
Может, про circle packing как-нибудь напишите?
Не вижу больше ни одной статьи, кроме этой, с тегом «вычислительная геометрия».
Может, про circle packing как-нибудь напишите?
По поводу сортировки на Питоне.
wiki.python.org/moin/HowTo/Sorting
Как-то так.
PS давно на питоне не писал, извиняюсь за глупые ошибки
wiki.python.org/moin/HowTo/Sorting
def cmp_to_key(mycmp):
'Convert a cmp= function into a key= function'
class K(object):
def __init__(self, obj, *args):
self.obj = obj
def __lt__(self, other):
return mycmp(self.obj, other.obj) < 0
def __gt__(self, other):
return mycmp(self.obj, other.obj) > 0
def __eq__(self, other):
return mycmp(self.obj, other.obj) == 0
def __le__(self, other):
return mycmp(self.obj, other.obj) <= 0
def __ge__(self, other):
return mycmp(self.obj, other.obj) >= 0
def __ne__(self, other):
return mycmp(self.obj, other.obj) != 0
return K
base = P[0]
del P[0]
P.sort(key = cmp_to_key(lambda x, y: rotate(A[base], A[x], A[y])))
P.insert(0, base)
Как-то так.
PS давно на питоне не писал, извиняюсь за глупые ошибки
Спасибо, сейчас опробуем!
Все заработало, отлично! Только порядок сортировки надо поменять:
Либо ключ (вернее, функцию сравнения) слегка изменить:
Работают оба варианта. А функция cmp_to_key, как написано по вашей ссылке, должна входить в модуль functools.
P.sort(key = cmp_to_key(lambda x, y: rotate(A[base], A[x], A[y])), reverse=True)
Либо ключ (вернее, функцию сравнения) слегка изменить:
P.sort(key = cmp_to_key(lambda x, y: rotate(A[base], A[y], A[x])))
Работают оба варианта. А функция cmp_to_key, как написано по вашей ссылке, должна входить в модуль functools.
помню, на областной олимпиаде по информатик была подобная задача. через тангенсы решили.
Да. Это, впрочем, старая задача, я ее видел на олимпиаде Челябинской области в 1991 году.
И решал через поиск максимального угла между соседними вершинами оболочки. И, что характерно, решил :)
И решал через поиск максимального угла между соседними вершинами оболочки. И, что характерно, решил :)
Сейчас на студенческих олимпиадах эту задачу в чистом виде не встретишь.
Обычно с применения алгоритма Грэхема следует начинать решение некоторых задач, чтобы перейти от произвольного множества точек к выпуклому многоугольнику.
Например, в задаче нахождения круга минимального радиуса, содержащей данное множество точек.
Или в задаче нахождения наибольшего по площади треугольника, вершинами которого являются точки из данного множества.
Обычно с применения алгоритма Грэхема следует начинать решение некоторых задач, чтобы перейти от произвольного множества точек к выпуклому многоугольнику.
Например, в задаче нахождения круга минимального радиуса, содержащей данное множество точек.
Или в задаче нахождения наибольшего по площади треугольника, вершинами которого являются точки из данного множества.
С интересом бы почитал книгу на подобные темы, написанную понятным языком (как эта статья). Возможно ктото может посоветовать? И по распознаванию образов тоже было бы интересно.
Спасибо за стастью.
Спасибо за стастью.
Отличный стиль — читается легко, несмотря на ненависть к питону. Хочется добавки, интересует нахождение мво на растре, наборе дисплейных регулярных пикселей- там стопудово грехэм быстрее, но может есть нечто оригинальное?
С помощью чего вы делали картинки?
Ой спасибо тебе добрый человек! Очень пост выручил!
Тут используется побочная/альтернативная терминология, введенная в начале статьи. В теории обобщенной выпуклости и аналогичных областях термин "облочка" ("hull") - однозначно определен, как минималное содержащее множдество, обладающее интересующими нас свойствами (напр. выпуклостью). То есть оболочки всегда минимальны по определению, а "минимальная выпуклая оболочка" - это уже бросающися в глаза пример "масла масляного". Соответственно в литературе обычно всегда ведется речь о просто выпуклой оболочке. Никто не называет ее минимальной.
Sign up to leave a comment.
Построение минимальных выпуклых оболочек