Viola Jones на собственной шкуре, часть 2. — Emotion? — OMG, Yes!!!
16 мин
Привет всем еще раз! Я решил сразу попробовать выпустить две статьи, практически в одно время, чтобы не прерывать цепь повествования, т.к. начало данной статьи очень важно!
Итак, многие ждали примеры моей программы и объяснения ее работы с точки зрения написания кода. Я же рассказываю последовательно, чтобы каждый смог ее повторить у себя на компьютере. Обращайте внимание побольше на обильные комментарии в коде, в них сила! И не бойтесь мега-мелкого скролла, т.к. информации много. Передислоцируйтесь в место с хорошим интернетом, в статье много схем и фотографий!
Итак, многие ждали примеры моей программы и объяснения ее работы с точки зрения написания кода. Я же рассказываю последовательно, чтобы каждый смог ее повторить у себя на компьютере. Обращайте внимание побольше на обильные комментарии в коде, в них сила! И не бойтесь мега-мелкого скролла, т.к. информации много. Передислоцируйтесь в место с хорошим интернетом, в статье много схем и фотографий!

 Как видно по дискуссиям на хабре, несколько десятков хабровчан прослушали курс ml-class.org Стэнфордского университета, который провел обаятельнейший профессор Andrew Ng. Я тоже с удовольствием прослушал этот курс. К сожалению, из лекций выпала очень интересная тема, заявленная в плане: комбинирование обучения с учителем и обучения без учителя. Как оказалось, профессор Ng опубликовал отличный курс по этой теме — Unsupervised Feature Learning and Deep Learning (спонтанное выделение признаков и глубокое обучение). Предлагаю краткий конспект этого курса, без строгого изложения и обилия формул. В
Как видно по дискуссиям на хабре, несколько десятков хабровчан прослушали курс ml-class.org Стэнфордского университета, который провел обаятельнейший профессор Andrew Ng. Я тоже с удовольствием прослушал этот курс. К сожалению, из лекций выпала очень интересная тема, заявленная в плане: комбинирование обучения с учителем и обучения без учителя. Как оказалось, профессор Ng опубликовал отличный курс по этой теме — Unsupervised Feature Learning and Deep Learning (спонтанное выделение признаков и глубокое обучение). Предлагаю краткий конспект этого курса, без строгого изложения и обилия формул. В 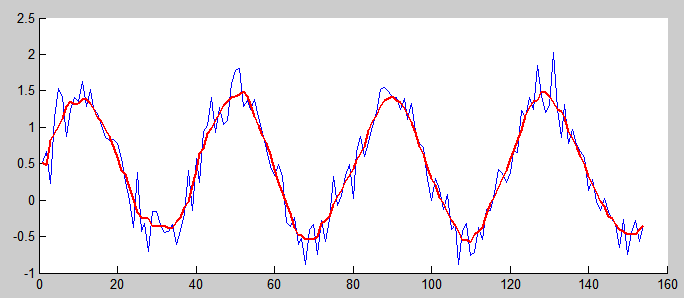
 В статье "
В статье "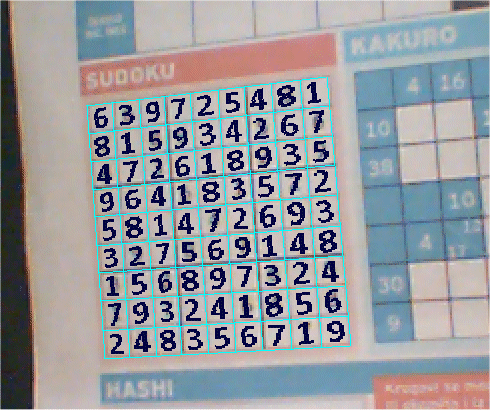
 теперь умеют умножать за
теперь умеют умножать за 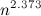 . Другими словами, доказано, что
. Другими словами, доказано, что 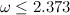 , где
, где 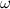 — экспонента умножения матриц. Доказала это совсем недавно
— экспонента умножения матриц. Доказала это совсем недавно 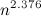 , полученную Копперсмитом и Виноградом в 1987 году. Я напишу про важность этого алгоритма совсем немножко. Тем, кому интересно узнать побольше, предлагается почитать посты
, полученную Копперсмитом и Виноградом в 1987 году. Я напишу про важность этого алгоритма совсем немножко. Тем, кому интересно узнать побольше, предлагается почитать посты 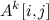 — количество (не обязательно простых!) путей длины k между вершинами i и j. Эта простая идея позволяет за время
— количество (не обязательно простых!) путей длины k между вершинами i и j. Эта простая идея позволяет за время 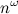 проверить, есть ли в графе треугольник (3-клика): нужно возвести матрицу смежности в куб (для этого потребуется два умножения матриц) и посмотреть на диагональ. Отметим, что речь здесь именно о теоретических оценках, поскольку продвинутые алгоритмы умножения матриц хоть и обгоняют асимптотически простой кубический алгоритм, но на практике дают ускорение только на огромных размерах матриц.
проверить, есть ли в графе треугольник (3-клика): нужно возвести матрицу смежности в куб (для этого потребуется два умножения матриц) и посмотреть на диагональ. Отметим, что речь здесь именно о теоретических оценках, поскольку продвинутые алгоритмы умножения матриц хоть и обгоняют асимптотически простой кубический алгоритм, но на практике дают ускорение только на огромных размерах матриц.
 В заметке обсуждаются алгоритмы решета для поиска простых чисел. Мы подробно рассмотрим классическое решето Эратосфена, особенности его реализации на популярных языках программирования, параллелизацию и оптимизацию, а затем опишем более современное и быстрое решето Аткина. Если материал о решете Эратосфена предназначен в первую очередь уберечь новичков от регулярного хождения по граблям, то алгоритм решета Аткина ранее на Хабрахабре не описывался.
В заметке обсуждаются алгоритмы решета для поиска простых чисел. Мы подробно рассмотрим классическое решето Эратосфена, особенности его реализации на популярных языках программирования, параллелизацию и оптимизацию, а затем опишем более современное и быстрое решето Аткина. Если материал о решете Эратосфена предназначен в первую очередь уберечь новичков от регулярного хождения по граблям, то алгоритм решета Аткина ранее на Хабрахабре не описывался.