В предыдущей части были освещены общедоступные вопросы, касающиеся SAT и P-NP: история проблемы, интуитивные определения классов и задач, указаны основные приложения SAT и основные последствия, в случаи решения P ?= NP (там же можно найти достаточное число ссылок на различный материал для самостоятельного изучения тематики).
В данной статье мы рассмотрим техническую сторону вопроса, а так же формализуем и представим в деталях материал из предыдущей статьи.

картинка из статьи Boolean Satisfiability: From Theoretical Hardness to Practical Success (Communications of ACM)
Для удобства прочтения и навигации предоставляем краткий обзор содержимого статьи.
В предыдущей работе, был рассмотрен только самый простой сценарий решения, что вызвало ряд интересных замечаний (автор выражает благодарность за интересные и полезные ссылки по данному вопросу). В данной статье рассмотрим всевозможные опции и их последствия, принимая во внимания комментарии и замечания к предыдущей работе.
Здесь довольно интересно с художественной точки зрения описана дискуссия вокруг различных вариантов решения.
Возможно несколько вариантов развития ситуации
Как и в предыдущем случае решение может быть конструктивным и не-конструктивным. Рассмотрим конструктивный случай (неконструктивный по структуре схож с предыдущем случаем)
Подробно и интересно об этом написано в статье Is P Versus NP Formally Independent? by Scott Aaronson (статья требует достаточной математической культуры для понимания; примерное время прочтения ~ 1/2 вечера). Приведем короткий обзор содержимого статьи.
Основной посыл статьи в следующем, может так оказаться, что обе гипотезы P = NP и P != NP согласуются с теорией множеств. Это может произойти в том случае, если P vs. NP независима от аксиоматики теории множеств, как например аксиома выбора независима от остальных аксиом теории множеств. С практической точки зрения это будет означать, что P != NP.
В теории сложности принято формулировать задачи в виде «проблем разрешимости» т.е. задачи, ответ на которые может быть только «да» или «нет». Классы P и NP формально определены в терминах языков и машин Тьюринга.
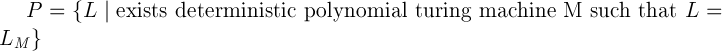
где LM — язык принимаемые машиной M.
Мы говорим, что определенная задача p принадлежит классу P, если существует детерминированная машина Тьюринга, которая принимает язык L(p) за полиномиальное число шагов.
С классом NP всё немного интересней, это класс задач, где корректность решения может быть проверена за полиномиальное время. Формально мы говорим, что язык L принадлежит NP, тогда и только тогда когда, существует детерминированная машина Тьюринга M, такая что для любой строки х верно:

где |y| — ограничен полиномом и M совершает полиномиальное число шагов. Для «y» существует специальный термин — сертификат. Фактически, определение читается следующим образом — задача принадлежит NP, если существует полиномиальное решение, корректность которого может быть проверена за полиномиальное время. Заметим, что данное определение несимметрично относительно вопроса, когда язык НЕ принадлежит NP т.е. вопрос НЕ принадлежит ли язык NP — это отдельный класс.
Что же за класс Co-NP? Co-NP — complement NP, интуитивно, это класс, задачи в котором являются отрицанием задач в NP. Если SAT, спрашивает, если ли такое присваивание истина/ложь переменным, что формула верна, то UNSAT спрашивает, верно ли, что для ВСЕХ присваиваний формула неверна? Т.е. иначе говоря, верно ли, что сертификата не существует.

или по-другому это можно сформулировать следующим образом:
NP — это коллекция языков с краткими сертификатами, подтверждающими принадлежность
Co-NP — это коллекция языков с краткими сертификатами, отвергающими принадлежность (= не существует сертификата принадлежности)
Если NP != Co-NP, то множество NP-полных и Co-NP-полных задач не пересекается (следствие Mahaney's theorem).
Подробнее о языках, машинах Тьюринга и определениях классов сложности можно прочитать в М.Гэри, Д.Джонсон: Вычислительные машины и труднорешаемые задачи (например, здесь)
Согласно современным представлениям отношение между NP, Co-NP и P выглядит следующим образом:
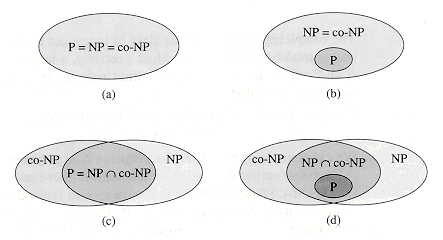
(картинка взята отсюда)
Большинство склоняются к варианту (d), но некоторые считают, что вероятны и другие опции e.g. Кнут в черновике The Art of Programming 4, 6A: Satisfibility — страница 1, сноска (*): "… автор данной книги, однако, подозревает, что полиномиальные алгоритмы [для SAT — прим. автора] действительно существуют, только они нам еще не известны...".
В предыдущей статье, было показано, что 2-SAT полиномиален, т.е. если мы ограничим каждое предложение (clause) двумя переменными, то задача может быть решена эффективно. Рассмотрим естественное обобщение этой задачи, что если у нас только часть предложений содержит 3 переменные?
Пусть p — это количество предложений с 3мя переменными к общему количеству предложений. Тогда задача 2+p SAT — это задача 3-SAT, в которой заранее зафиксировано количество предложений с 3мя переменными т.е. p, соответственно (1 — p) предложений имеют 1 или 2 переменные.
С теоретической точки зрения, даже если p — это концентрация барбарийской утки в оциллококцинуме т.е. любое положительное число, то задача NP полна, однако на практике это выглядит совершенно иначе.
Пусть по оси X — общее количество переменных в формуле, по оси Y — «вычислительная стоимость» решения для данной формулы (обычно это количество вызовов\решений state-of-the-art алгоритма SAT-solver, см. краткое описание DPLL и CDCL в предыдущей статье).

(график взят из работы 2+P-SAT: Relation of typical-case complexity to the nature of the phase transition).
Если p <= 0.4, то задача полиномиальна, даже более того, линейна по входным данным. Если p > 0.4, то мы наблюдаем поведение схожее с классическим 3-SAT. Для того, чтобы объяснить данный эффект рассмотрим классический алгоритм DPLL (взято из слайдов Armin Biere):

Рассмотрим простой пример

Пусть алгоритм, выбрал x2 = 1
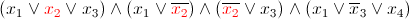
Тогда формула упрощается и у нас есть два предложения с единственной переменной — значит, boolean constraint propagation выбирает один из них, например x3 и присваивает единственное доступное ему значение
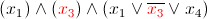
после присваивания x3=1, BCP снова находит предложение с единственной переменной x1, и присваивает x1=1

Таким образом, после единственного решения SAT solver, boolean constraint propagation позволяет найти решение всей формулы. Происходит это прежде всего потому, что решение на переменную в предложении с двумя переменными, фактически однозначно определяет значение еще одной переменной, что вызывает целый каскад присваиваний и BCP эффективно уменьшает формулу. Если подобный каскад покрывает достаточное количество переменных в формуле, то решение является линейным.
Еще одна интересная зависимость это так называемая clause-variable-ratio: соотношение числа предложений к числу переменных. Интуитивно, чем больше предложений, тем больше ограничений, тем вероятнее, что формулы невыполнима — слишком много ограничений. Про такую проблему говорят, что она overconstrainted. Если же предложений мало, а переменных много, то значит, что степеней свободы много, а ограничений мало. Это позволяет легко найти решение, и вероятно, что формула выполнима. Про неё говорят, что она underconstrained.
Так как мы уже рассмотрели 2+p SAT, то было бы также интересно учесть параметр p в данной зависимости, как степень «линейности» проблемы, чем больше p, тем менее эффективен boolean constraint propagation и тем сложнее найти решение.
SAT/UNSAT переход для 2+p SAT
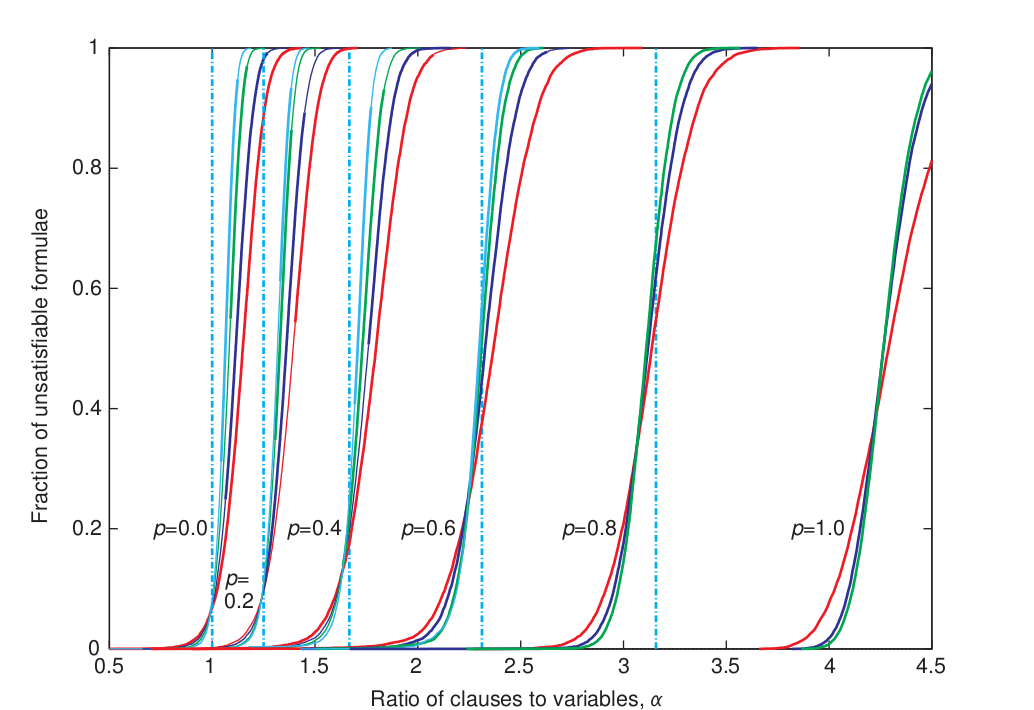
График из статьи Nature: Determining computational complexity from characteristic `phase transitions' by Remi Monasson, Riccardo Zecchina, Scott Kirkpatrick, Bart Selman and Lidror Troyanskyk
На самом деле, этот график даёт нам нечто большее, чем мы думаем: он позволяет генерировать «сложные» случайные формулы. Если формула находится где-то в центре между SAT и UNSAT, это значит, что для неё сложно найти модель и сложно сгенерировать доказательство невыполнимости.
Зависимость числа вызовов DPLL от позиции SAT/UNSAT перехода имеет следующий вид
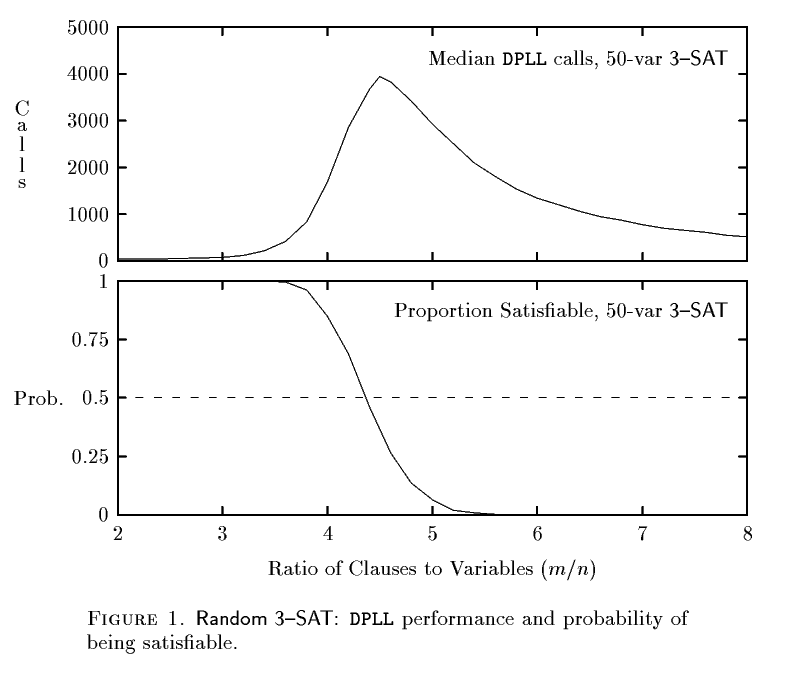
График из статьи Finding Hard Instances of the Satis ability Problem: A Survey by S. Cook, D. Mitchell
Даже на описание основных принципов, алгоритмов и эвристик уйдет не одна сотня страниц, поэтому ограничимся одним из описанием одного из самых популярных и ключевых алгоритмов SAT: CDCL — Conflict Driven Clause Learning. Как следует из названия одна из главных особенностей этого алгоритма — это способность запоминать решения, которые не ведут к решению, а именно алгоритм запоминает их в виде предложений. Если мы приняли решения x1 = 1, x2 = 2, x3 = 1 и это ведет к конфликту, то CDCL запомнит отрицание конфликтной комбинации.
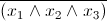
по правилу Де Моргана приводим к CNF виду
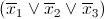
и добавляем его к формуле

Таким образом две ключевые составляющие CDCL: граф импликаций вместе со стеком принятых решений и работа с конфликтными комбинациями. Как правило, после принятия решения, алгоритм проводит все возможные детерминированные вычисления и приходит к конфликту. Граф импликаций и стек решений, показывают, какая комбинация и решение на каком этапе привело к конфликту, на основе этого происходит генерация конфликтного предложения — отсюда и название Conflict Driven Clause Learning, алгоритм эффективно находит конфликтные комбинации, выучивает их и принимает решения, учитывая конфликтные комбинации.
Подробнее рассмотрим пример работы CDCL алгоритма:
from Masahiro Sakai
Подробнее о CDCL написано в следующих работах:
Handbook of Satisfiability: Chapter 4. Conflict-Driven Clause Learning SAT Solvers by Joao Marques-Silva, Ines Lynce and Sharad Malik
SAT/SMT Summer School 2013 слайды автора CDCL: CDCL SAT Solvers & SAT-Based Problem Solving
Детальное и достаточное техническое описание работы алгоритма и внутренних структур: Practical SAT Solving: Conflict-driven SAT solvers
Во-первых, нужно ответить на ряд вопросов на соответствие решения здравому смыслу
Допустим, что все эти условия выполнены, тогда второе, что будет считаться признанным решением? Публикация в журнале «Автоматика и механика»? Есть несколько конференций, подходящих для задачи P vs NP:
STOC, the Annual ACM Symposium on Theory of Computing
TAGL, ACM Transactions on Algorithms
FOCS, The IEEE Annual Symposium on Foundations of Computer Science
Если они (любая из этих конференций), признают ваше решение, можете смело рассчитывать на свой миллион — до этого момента решение считается одним из многих неправильных решений P vs. NP.
Интересный roadmap (точнее даже интерактивный список вопросов) по вопросу проверки P vs. NP решений представлен здесь.
Если давать краткий ответ, то потому, что статья не отвечает ни на один из вопросов из списка «здравого смысла»:
Далее, допустим, что работа будет исправлена, тогда по-прежнему не имеет смысла писать открытые письма никому — современная наука так не работает, это ваша задача убедить общественность в правильности решения. Сделать это можно только через призму экспертного мнения, см. конференции описанные выше.
Обычно хорошо и доступно всё объясняют в SAT/SMT летних школах:
материалы школы 2013
материалы школы 2012
Скоро будет свежий Кнут про SAT — доступен черновик: The Art of Programming 4, 6A: Satisfibility
Большое количество ссылок присутствует в предыдущем посте Зачем нам всем нужен SAT и все эти P-NP (часть первая)
Ключевые приведем здесь:
о SAT-solver'ах:
SAT Solvers: A Condensed History
Understanding Modern SAT Solvers — автор Armin Biere, пожалуй, самый известный разработчик SAT Solver'ов в мире. Дональд Кнут, который сейчас пишет «The Art of Computer Programming: Volume 4B, Pre-fascicle 6A Satisfiability», говорит, что по многим вопросам консультируется именно у него.
Towards a new era of SAT Solvers
об истории NP:
The History and Status of the P versus NP Question by Michael Sipser
P versus NP by Elvira Mayordomo
Один из наиболее известных и уважаемых трудов по теории сложности:
Гэри М., Джонсон Д. — Вычислительные машины и труднорешаемые задачи [1982]
Нестыковка SAT, реляционной алгебры и проблемы останова.
Дано три утверждения:
1. Логика первого порядка и реляционная алгебра имеют одинаковую «вычислительную сложность» т. е. если задача имеет сложность Х в одном формализме, то существует её выражение в другом формализме с такой же сложностью (ссылка).
2. Реляционная алгебра не способна выразить транзитивное замыкание – задача в классе P (relational algebra: transitive closure )
3. SAT для логики первого порядка эквивалентен проблеме останова и алгоритмически неразрешим (ссылка).
Вопрос: Как такое может быть?
В данной статье мы рассмотрим техническую сторону вопроса, а так же формализуем и представим в деталях материал из предыдущей статьи.

картинка из статьи Boolean Satisfiability: From Theoretical Hardness to Practical Success (Communications of ACM)
Структура статьи
Для удобства прочтения и навигации предоставляем краткий обзор содержимого статьи.
- Общедоступный материал (первая часть)
- Почему SAT важен для нас всех? Приложения/Интересные NP задачи и SAT
- История SAT и NP-полноты
- «Интуитивное определение» SAT, NP и P
- Что будет, если… P != NP, P = NP
- 2-SAT полиномиален: алгоритм и интуиция
- Задачка на подумать
- Специализированный материал (данная статья)
- Что будет, если… (в деталях)
- Формальное определение. Несимметричность проблемы разрешимости для NP. Класс CoNP.
- 2+p-SAT полиномиален?
- Зависимость сложности от числа переменных
- О современных SAT solver'ах
- Я решил P vs. NP, что мне делать? Куда писать?
- Теоремы о невыразимости: почему статью Романова ожидает reject
- Что почитать?
- Задачка на подумать
Что будет, если…
В предыдущей работе, был рассмотрен только самый простой сценарий решения, что вызвало ряд интересных замечаний (автор выражает благодарность за интересные и полезные ссылки по данному вопросу). В данной статье рассмотрим всевозможные опции и их последствия, принимая во внимания комментарии и замечания к предыдущей работе.
Здесь довольно интересно с художественной точки зрения описана дискуссия вокруг различных вариантов решения.
P = NP
Возможно несколько вариантов развития ситуации
- Решение конструктивное
- Полином имеет невысокую степень и умеренные коэффициенты: тогда подробности описаны в части P = NP предыдущей статьи; вкратце: рухнет вся криптография
- Полином имеет высокую степень — тогда ничего не изменится и с практической точки зрения P != NP
- Решение неконструктивное
- Если мы не сможем получить алгоритм из данного доказательства, то с практической точки зрения P != NP
- Если можем, то вопрос P ?= NP, трансформируется в вопрос времени и создания алгоритма из доказательства
P != NP
Как и в предыдущем случае решение может быть конструктивным и не-конструктивным. Рассмотрим конструктивный случай (неконструктивный по структуре схож с предыдущем случаем)
- Сложность решения всегда экспоненциальная: никаких изменений, текущая картина мира полностью сохранится, никаких изменений в алгоритмах
- Сложность решения не-всегда экспоненциальная (см. этот пост), а для достаточного количества случаев полиномиальная. В данном случае, практически невозможно однозначно предсказать, что произойдет и можно только спекулировать: если задача факторизации попадает в «класс легких задач», то с практической точки зрения это будет эквивалентно P = NP для атаки на RSA.
- Сложность решения умеренная или низкая (e.g. nlog(n)), в данном случае с практической точки зрения это будет эквивалентно P = NP
P vs. NP не разрешима в аксиоматике ZFC
Подробно и интересно об этом написано в статье Is P Versus NP Formally Independent? by Scott Aaronson (статья требует достаточной математической культуры для понимания; примерное время прочтения ~ 1/2 вечера). Приведем короткий обзор содержимого статьи.
Основной посыл статьи в следующем, может так оказаться, что обе гипотезы P = NP и P != NP согласуются с теорией множеств. Это может произойти в том случае, если P vs. NP независима от аксиоматики теории множеств, как например аксиома выбора независима от остальных аксиом теории множеств. С практической точки зрения это будет означать, что P != NP.
Формальное определение. Несимметричность проблемы разрешимости для NP. Класс CoNP.
В теории сложности принято формулировать задачи в виде «проблем разрешимости» т.е. задачи, ответ на которые может быть только «да» или «нет». Классы P и NP формально определены в терминах языков и машин Тьюринга.
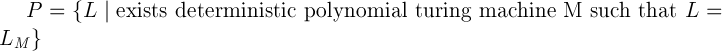
где LM — язык принимаемые машиной M.
Мы говорим, что определенная задача p принадлежит классу P, если существует детерминированная машина Тьюринга, которая принимает язык L(p) за полиномиальное число шагов.
С классом NP всё немного интересней, это класс задач, где корректность решения может быть проверена за полиномиальное время. Формально мы говорим, что язык L принадлежит NP, тогда и только тогда когда, существует детерминированная машина Тьюринга M, такая что для любой строки х верно:

где |y| — ограничен полиномом и M совершает полиномиальное число шагов. Для «y» существует специальный термин — сертификат. Фактически, определение читается следующим образом — задача принадлежит NP, если существует полиномиальное решение, корректность которого может быть проверена за полиномиальное время. Заметим, что данное определение несимметрично относительно вопроса, когда язык НЕ принадлежит NP т.е. вопрос НЕ принадлежит ли язык NP — это отдельный класс.
Что же за класс Co-NP? Co-NP — complement NP, интуитивно, это класс, задачи в котором являются отрицанием задач в NP. Если SAT, спрашивает, если ли такое присваивание истина/ложь переменным, что формула верна, то UNSAT спрашивает, верно ли, что для ВСЕХ присваиваний формула неверна? Т.е. иначе говоря, верно ли, что сертификата не существует.

или по-другому это можно сформулировать следующим образом:
NP — это коллекция языков с краткими сертификатами, подтверждающими принадлежность
Co-NP — это коллекция языков с краткими сертификатами, отвергающими принадлежность (= не существует сертификата принадлежности)
Если NP != Co-NP, то множество NP-полных и Co-NP-полных задач не пересекается (следствие Mahaney's theorem).
Подробнее о языках, машинах Тьюринга и определениях классов сложности можно прочитать в М.Гэри, Д.Джонсон: Вычислительные машины и труднорешаемые задачи (например, здесь)
Согласно современным представлениям отношение между NP, Co-NP и P выглядит следующим образом:

(картинка взята отсюда)
Большинство склоняются к варианту (d), но некоторые считают, что вероятны и другие опции e.g. Кнут в черновике The Art of Programming 4, 6A: Satisfibility — страница 1, сноска (*): "… автор данной книги, однако, подозревает, что полиномиальные алгоритмы [для SAT — прим. автора] действительно существуют, только они нам еще не известны...".
2+p-SAT полиномиален?
В предыдущей статье, было показано, что 2-SAT полиномиален, т.е. если мы ограничим каждое предложение (clause) двумя переменными, то задача может быть решена эффективно. Рассмотрим естественное обобщение этой задачи, что если у нас только часть предложений содержит 3 переменные?
Пусть p — это количество предложений с 3мя переменными к общему количеству предложений. Тогда задача 2+p SAT — это задача 3-SAT, в которой заранее зафиксировано количество предложений с 3мя переменными т.е. p, соответственно (1 — p) предложений имеют 1 или 2 переменные.
С теоретической точки зрения, даже если p — это концентрация барбарийской утки в оциллококцинуме т.е. любое положительное число, то задача NP полна, однако на практике это выглядит совершенно иначе.
Пусть по оси X — общее количество переменных в формуле, по оси Y — «вычислительная стоимость» решения для данной формулы (обычно это количество вызовов\решений state-of-the-art алгоритма SAT-solver, см. краткое описание DPLL и CDCL в предыдущей статье).

(график взят из работы 2+P-SAT: Relation of typical-case complexity to the nature of the phase transition).
Если p <= 0.4, то задача полиномиальна, даже более того, линейна по входным данным. Если p > 0.4, то мы наблюдаем поведение схожее с классическим 3-SAT. Для того, чтобы объяснить данный эффект рассмотрим классический алгоритм DPLL (взято из слайдов Armin Biere):

Рассмотрим простой пример

Пусть алгоритм, выбрал x2 = 1
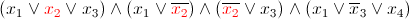
Тогда формула упрощается и у нас есть два предложения с единственной переменной — значит, boolean constraint propagation выбирает один из них, например x3 и присваивает единственное доступное ему значение
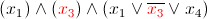
после присваивания x3=1, BCP снова находит предложение с единственной переменной x1, и присваивает x1=1

Таким образом, после единственного решения SAT solver, boolean constraint propagation позволяет найти решение всей формулы. Происходит это прежде всего потому, что решение на переменную в предложении с двумя переменными, фактически однозначно определяет значение еще одной переменной, что вызывает целый каскад присваиваний и BCP эффективно уменьшает формулу. Если подобный каскад покрывает достаточное количество переменных в формуле, то решение является линейным.
Зависимость сложности от числа переменных
Еще одна интересная зависимость это так называемая clause-variable-ratio: соотношение числа предложений к числу переменных. Интуитивно, чем больше предложений, тем больше ограничений, тем вероятнее, что формулы невыполнима — слишком много ограничений. Про такую проблему говорят, что она overconstrainted. Если же предложений мало, а переменных много, то значит, что степеней свободы много, а ограничений мало. Это позволяет легко найти решение, и вероятно, что формула выполнима. Про неё говорят, что она underconstrained.
Так как мы уже рассмотрели 2+p SAT, то было бы также интересно учесть параметр p в данной зависимости, как степень «линейности» проблемы, чем больше p, тем менее эффективен boolean constraint propagation и тем сложнее найти решение.
SAT/UNSAT переход для 2+p SAT

График из статьи Nature: Determining computational complexity from characteristic `phase transitions' by Remi Monasson, Riccardo Zecchina, Scott Kirkpatrick, Bart Selman and Lidror Troyanskyk
На самом деле, этот график даёт нам нечто большее, чем мы думаем: он позволяет генерировать «сложные» случайные формулы. Если формула находится где-то в центре между SAT и UNSAT, это значит, что для неё сложно найти модель и сложно сгенерировать доказательство невыполнимости.
Зависимость числа вызовов DPLL от позиции SAT/UNSAT перехода имеет следующий вид

График из статьи Finding Hard Instances of the Satis ability Problem: A Survey by S. Cook, D. Mitchell
О современных SAT solver'ах
Даже на описание основных принципов, алгоритмов и эвристик уйдет не одна сотня страниц, поэтому ограничимся одним из описанием одного из самых популярных и ключевых алгоритмов SAT: CDCL — Conflict Driven Clause Learning. Как следует из названия одна из главных особенностей этого алгоритма — это способность запоминать решения, которые не ведут к решению, а именно алгоритм запоминает их в виде предложений. Если мы приняли решения x1 = 1, x2 = 2, x3 = 1 и это ведет к конфликту, то CDCL запомнит отрицание конфликтной комбинации.
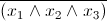
по правилу Де Моргана приводим к CNF виду
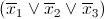
и добавляем его к формуле

Таким образом две ключевые составляющие CDCL: граф импликаций вместе со стеком принятых решений и работа с конфликтными комбинациями. Как правило, после принятия решения, алгоритм проводит все возможные детерминированные вычисления и приходит к конфликту. Граф импликаций и стек решений, показывают, какая комбинация и решение на каком этапе привело к конфликту, на основе этого происходит генерация конфликтного предложения — отсюда и название Conflict Driven Clause Learning, алгоритм эффективно находит конфликтные комбинации, выучивает их и принимает решения, учитывая конфликтные комбинации.
Подробнее рассмотрим пример работы CDCL алгоритма:
from Masahiro Sakai
Подробнее о CDCL написано в следующих работах:
Handbook of Satisfiability: Chapter 4. Conflict-Driven Clause Learning SAT Solvers by Joao Marques-Silva, Ines Lynce and Sharad Malik
SAT/SMT Summer School 2013 слайды автора CDCL: CDCL SAT Solvers & SAT-Based Problem Solving
Детальное и достаточное техническое описание работы алгоритма и внутренних структур: Practical SAT Solving: Conflict-driven SAT solvers
Я решил P vs. NP, что мне делать? Куда писать?
Во-первых, нужно ответить на ряд вопросов на соответствие решения здравому смыслу
- Может ли работа объяснить почему другие попытки решить задачу провалились, а наша работа нет
- Как данная работа обходит теоремы о невыразимости т.е. явно показать, что данные теоремы (e.g. Baker-Gill-Solovay theorem) к данной работе не применимы
- Если P = NP и доказательство конструктивно, то обязателен прототип, иначе никто не поверит в решение
- Работа самодостаточна и доступна эксперту для понимания т.е. она содержит все необходимые определения, доказательства в развернутом виде (задача тысячелетия, написанная на 3х страницах иероглифами и недоступным языком, вызывает подозрение и желание у проверяющего отравить её в корзину )
- Авторы обладают хорошим пониманием теории сложности i.e. знакомы со всеми основными трудами и работами и знают, что происходило в данной научной области в последние годы
Допустим, что все эти условия выполнены, тогда второе, что будет считаться признанным решением? Публикация в журнале «Автоматика и механика»? Есть несколько конференций, подходящих для задачи P vs NP:
STOC, the Annual ACM Symposium on Theory of Computing
TAGL, ACM Transactions on Algorithms
FOCS, The IEEE Annual Symposium on Foundations of Computer Science
Если они (любая из этих конференций), признают ваше решение, можете смело рассчитывать на свой миллион — до этого момента решение считается одним из многих неправильных решений P vs. NP.
Интересный roadmap (точнее даже интерактивный список вопросов) по вопросу проверки P vs. NP решений представлен здесь.
Почему статью Романова ожидает reject
Если давать краткий ответ, то потому, что статья не отвечает ни на один из вопросов из списка «здравого смысла»:
- В статье вообще отсутствует «related work», создается впечатление, что 40 лет в теории сложности вообще не было прогресса (автор только на себя сослался три раза): для примера, можно взглянуть на The NP-Completeness Column: The Many Limits on Approximation by David S. Johnson, сжато кратко по делу рассказывает про все связанные работы, нормальная качественная работа в TAGL
- Данная работа допускает алгебраическое представление (таблички из переменных, граф на этих табличках и чуть-ли не conjunctive query для проверки свойств) — напрямую применима теорема Aaronson-Wigderson (обобщающая теорему Baker-Gill-Solovay) о неразрешимости P vs. NP с помощью алгебраических методов. Кстати, если у проверяющих есть сомнение, что вы игнорируете такие результаты намеренно, это будет интерпретировано против отправленной работы
- Где прототип не убегающий к экспоненте в асимптотике?
- Где псевдокод алгоритма? Где полноценный рабочий пример: входные данные — известный сложный пример, поэтапно показана работа алгоритма и выходные данные? Где формализация? в статье на 17 страниц две формулы вида (a => b) и неформальные фразы в духе: «grouping the lines of F with identical numbers of three non-empty columns;»
- Отсутствуют ключевые ссылки в работе, например, на работы Левина-Кука.
Далее, допустим, что работа будет исправлена, тогда по-прежнему не имеет смысла писать открытые письма никому — современная наука так не работает, это ваша задача убедить общественность в правильности решения. Сделать это можно только через призму экспертного мнения, см. конференции описанные выше.
Что почитать?
Обычно хорошо и доступно всё объясняют в SAT/SMT летних школах:
материалы школы 2013
материалы школы 2012
Скоро будет свежий Кнут про SAT — доступен черновик: The Art of Programming 4, 6A: Satisfibility
Большое количество ссылок присутствует в предыдущем посте Зачем нам всем нужен SAT и все эти P-NP (часть первая)
Ключевые приведем здесь:
о SAT-solver'ах:
SAT Solvers: A Condensed History
Understanding Modern SAT Solvers — автор Armin Biere, пожалуй, самый известный разработчик SAT Solver'ов в мире. Дональд Кнут, который сейчас пишет «The Art of Computer Programming: Volume 4B, Pre-fascicle 6A Satisfiability», говорит, что по многим вопросам консультируется именно у него.
Towards a new era of SAT Solvers
об истории NP:
The History and Status of the P versus NP Question by Michael Sipser
P versus NP by Elvira Mayordomo
Один из наиболее известных и уважаемых трудов по теории сложности:
Гэри М., Джонсон Д. — Вычислительные машины и труднорешаемые задачи [1982]
Задачка на подумать
Нестыковка SAT, реляционной алгебры и проблемы останова.
Дано три утверждения:
1. Логика первого порядка и реляционная алгебра имеют одинаковую «вычислительную сложность» т. е. если задача имеет сложность Х в одном формализме, то существует её выражение в другом формализме с такой же сложностью (ссылка).
2. Реляционная алгебра не способна выразить транзитивное замыкание – задача в классе P (relational algebra: transitive closure )
3. SAT для логики первого порядка эквивалентен проблеме останова и алгоритмически неразрешим (ссылка).
Вопрос: Как такое может быть?
