В 2011-2013 гг. австралийский писатель Грег Иган (Greg Egan) опубликовал трилогию Orthogonal (The Clockwork Rocket, The Ethernal Flame, The Arrows of Time). В книгах описан удивительный мир, в котором нет жидкостей и электрических зарядов, обитают четырёхглазые разумные существа, способные менять форму и размножающиеся делением, использующие воздух не для химических реакций, а для охлаждения своего тела, а свет — для передачи нервных импульсов. Скорость света в этом мире непостоянна: фиолетовые фотоны движутся заметно быстрее красных. Поэтому звёзды выглядят не как белые точки, а как радужные полоски Ещё в первой книге герои выяснили, что причина такого поведения света заключается в свойствах пространства-времени их вселенной: в отличие от нашего мира, который является пространством Минковского, у них пространственная и временная координаты полностью равноправны. Любое тело движется по своей траектории в четырёхмерном пространстве-времени с постоянной скоростью, равномерное движение там выглядит, как прямая, а ускоренное — как дуга. Например, полёт космического корабля к другой звезде и обратно можно представить такой картинкой:
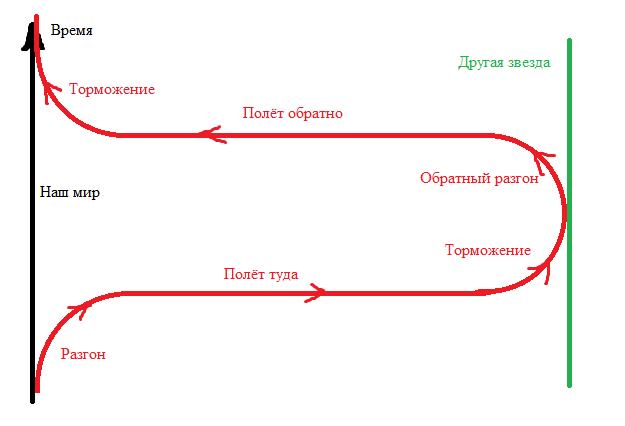
Тягу корабля во время разгона и торможения мы считаем постоянной, и в этом случае траектория его движения в пространстве-времени будет дугой окружности. За конечное время корабль достигнет бесконечной (по часам неподвижного наблюдателя) скорости, и основная часть полёта пройдёт за нулевое время. При этом время для пассажиров корабля будет идти как обычно, и измерить его можно по длине траектории на рисунке. Когда корабль вернётся в точку старта, окажется, что на родной планете прошло всего несколько лет, в то время, как для пассажиров корабля могли пройти века. Более того, если фазы разгона/торможения будут длиться чуть дольше, то корабль может вернуться в тот же момент, когда он стартовал, а может даже раньше:
Правда, Вселенной придётся как-то решать возникающие при этом парадоксы, и эти решения могут оказаться неожиданными для обитателей планеты.
Фотоны подчиняются тем же законам, что и остальные тела. Они отличаются наличием собственных колебаний. Все фотоны одинаковы, и в собственной системе отсчёта они имеют одинаковую частоту (и нулевую длину волны). Но когда наблюдатель видит фотоны, двигавшиеся с разной скоростью, то их частоты ему кажутся разными. У красного света (самого медленного) частота и длина волны минимальна, а у фиолетового — максимальна:
Здесь красная линия — траектория красного фотона, а фиолетовая — соответственно, траектория фиолетового. Глаз видит фотоны, траектории которых находятся между этими линиями.
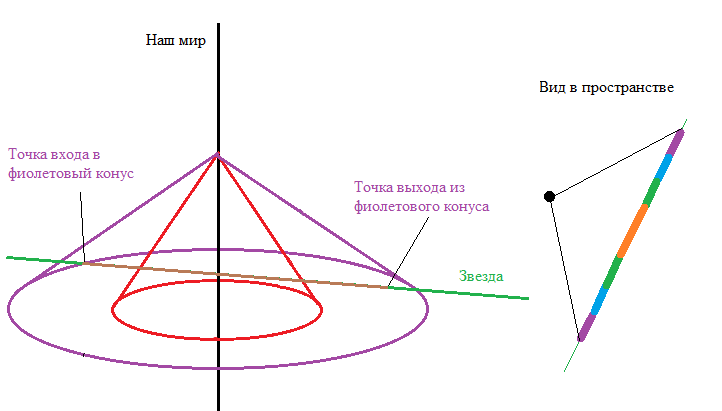
Герои книги видят свет в диапазоне скорости от 76/144 до 192/144 от скорости синего света (синие фотоны — это те, которые летят в пространстве-времени под углом 45 градусов к наблюдателю, то есть, их видимая скорость в пространстве равна скорости любой системы отсчёта в пространстве-времени). Таким образом, наблюдатель видит только те фотоны, траектория которых лежит между двумя конусами:
Половина угла при вершине внутреннего (красного) конуса составляет 27 градусов, а внешнего (фиолетового) — 54 градуса. Если траектория звезды пересекает это пространство, то звезду видно:
Здесь рассматривалась медленно движущаяся звезда. Если скорость звезды станет больше, то траектория будет состоять из двух частей:
Вскоре после начала трилогии в небе стали появляться странные звёзды — хартлеры (Hurtler — вредитель?). Они возникали как фиолетовые точки, от которых быстро расходились радужные полоски в две стороны:
Герои предположили (и правильно), что хартлеры — это звёзды, траектория которых перпендикулярна траектории их мира. То есть, каждая такая звезда существует только в один момент времени, но занимает при этом всю свою траекторию. В пространстве-времени это могло бы выглядеть так:
Но если внимательно посмотреть на эту картину, окажется, что половина траектории, направленная в сторону движения хартлера, образована фотонами, которые в системе отсчёта хартлера летят назад во времени! Судя по содержанию третьей книги, таких фотонов звёзды не испускают, поэтому в действительности картина должна выглядеть так:
Мне стало интересно, как будет выглядеть такая Вселенная, если перемещаться по ней в очень маневренном корабле. Для этого я решил написать игру с простейшим сюжетом — есть Вселенная, в ней несколько звёзд, которые надо посетить и погасить (просто пролетев рядом).
Первый вопрос был — какую выбрать форму пространства-времени. Герои трилогии быстро пришли к выводу, что Вселенная должна быть конечной, но долго сомневались, какой именно. В итоге они пришли к выводу, что это должна быть четырёхмерная сфера (т.е. сфера в 5-мерном пространстве). Правда, им по каким-то причинам понадобилось, чтобы в ней были области с отрицательной кривизной (иначе возникали какие-то проблемы с энтропией), то есть, сфера должна быть искаженной формы. Но я для простоты взял обычную однородную сферу.
Положение и скорость корабля описываются парой перпендикулярных векторов. Вектор P определяет текущее положение в пространстве времени, V — направление дрейфа (скорость дрейфа всегда одинакова). Кроме того, нужны три вектора X, Y, Z, определяющие ориентацию корабля в пространстве (и изображение на экране). Все вектора берутся в 5-мерном пространстве, имеют длину 1 и перпендикулярны друг другу. Таким образом, корабль описывается ортогональной матрицей 5*5.
Оказывается, что все движения и манёвры корабля в этом представлении — всего лишь повороты матрицы в координатных плоскостях. Общий дрейф — поворот в плоскости (P,V) (векторы X,Y,Z остаются неизменными), разгон и торможение в 3D — повороты в плоскости (V,Z), боковые ускорения — повороты в (V,X) и в (V,Y), смена ориентации корабля — вращения в (X,Z) и (Y,Z). Скорости вращения определяются общими параметрами игры, и их можно менять на панели управления.
Траектория звезды — тоже пара перпендикулярных векторов (P0,V0). В любой момент времени T (по часам самой звезды) её положение будет P1=P0*cos(T)+V0*sin(T), а скорость дрейфа — V1=V0*cos(T)-P0*sin(T). Чтобы получить изображение звезды, нам нужно определить параметры фотона, выпущенного из точки (P1,V1) и долетевшего до нашей точки (P,V): какого он будет цвета и с какой стороны прилетит. Для этого нам достаточно соединить точки P и P1 дугой большого круга и посмотреть, в какую сторону она выходит из точки P и с какой стороны входит в P1.
Для простоты будем считать, что фотон не может пролететь больше четверти круга. В самом деле, в книге ничего не сказано ни об изображении звезды, видимом с ночной стороны планеты, ни о фантомных звёздах с противоположного края Вселенной, свет от которых сфокусировался в окрестности мира героев трилогии. Это значит, что нам достаточно рассмотреть случай, когда угол между векторами P и P1 острый, т.е. (P,P1)>0. Оказывается, что во-первых, нужно выполнение условия (P,V1)>0 — иначе звезде пришлось бы излучать фотон в прошлое, во-вторых, (P1,V)>0 — иначе фотон прилетит к нам из будущего, и без специальных средств мы его увидеть не сможем.
После этого нам достаточно спроектировать вектор P1 на пространство (V,X,Y,Z) (Касательное к сфере в точке P). Пусть получается вектор S=(v,x,y,z). Тогда длина L вектора S соответствует расстоянию, которое пролетел фотон (точнее, равна его синусу), величина v/L — косинус угла между траекторией фотона и нашей траекторией в пространстве-времени, который определяет цвет фотона, а (x,y,z) — направление, с которого фотон прилетел — и мы можем изобразить его привычными методами.
Оказывается, что ловить звёзды совсем не просто. Простейший случай — когда звезда близко, и наши скорости отличаются не очень сильно (как было на первом рисунке с конусами). С помощью боковых двигателей мы без труда можем устранить поперечные скорости. Звезда на экране из радужной полоски превратится в точку, наши траектории в пространстве-времени окажутся в одной плоскости, и мы будем лететь к звезде ()или от неё — заранее сказать трудно).
Естественное желание — нацелиться на звезду и начать разгоняться. Но что при этом произойдёт?
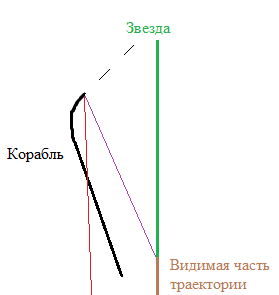
Видно, что участок траектории, который мы видим, становится всё дальше — фактически, мы начинаем видеть всё более далёкое прошлое звезды. Кроме того, видимая звезда удаляется, и становится всё меньше и тусклее. И если у нас есть хоть небольшое боковое смещение, то мы увидим, что красная часть траектории сокращается, прекращаясь на зелёном, а потом и на синем участке спектра.
В этот момент можно чуть-чуть притормозить и ждать, пока звезда не станет больше в размерах. А потом начинать её ловить. Но что будет, если мы промахнёмся?
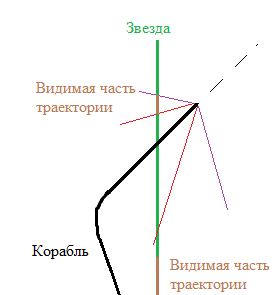
С той стороны, куда мы смотрели, фиолетовая часть трека неожиданно сменится на красную, и мы увидим, что она удаляется. А сама звезда окажется с противоположной от нас стороны. Поэтому нам нужно разворачивать корабль и двигаться к звезде снова.
Но поймать близкую звезду не очень сложно. Проблемы начинаются, когда звезда далеко, и мы видим длинный и тонкий радужный след. Где искать звезду, куда лететь — понять совершенно невозможно. Иногда мне это удаётся. Чаще нет.
Если хотите поэкспериментировать с этим космосом — exe-файл можно взять здесь (для .NET 3.5), а исходники — здесь.
А более подробное описание законов физики этого мира (вплоть до квантового уровня) есть на сайте автора трилогии: www.gregegan.net
