Scorobey 11 авг 2018 в 22:09

Построение орбит небесных тел средствами Python

9 мин

28K

Python*Алгоритмы*Математика*Разработка под Windows*Астрономия

Туториал

Системы отсчёта для определения орбиты

Для нахождения траекторий относительных движений в классической механике используется предположение об абсолютности времени во всех системах отсчета (как инерциальных, так и неинерциальных).

Используя данное предположение, рассмотрим движение одной и той же точки в двух различных системах отсчета $inline$ и $K^{'}$ , из которых вторая движется относительно первой с произвольной скоростью $\vec{V(t)}=\dot{\vec{R(t)}}$ , где $\vec{R(t)}$ радиус-вектор, описывающий положение точки начала системы координат $K^{'}$ относительно системы отсчета $inline$ ).

Будем описывать движение точки в системе $K^{'}$ радиус-вектором $\vec{r^{'}}(t)$ , направленным из начала координат системы $K^{'}$ в текущее положение точки. Тогда движение рассматриваемой точки относительно системы отсчета $inline$ описывается радиус-вектором $\vec{r(t)}$ :

$\vec{r}(t)=\vec{r^{'}}(t)+\vec{R}(t)$ , (1)

а относительная скорость $\vec{v(t)}$

$\vec{v}(t)=\dot{\vec{r^{'}}}(t)+\dot{\vec{R}}(t)$ ,(2)

где $\dot{\vec{r^{'}}}(t)$ — скорость точки относительно системы $K^{'}$ ; $\dot{\vec{R}}(t)$ -скорость движения системы отсчета $K^{'}$ относительно системы отсчета $inline$ .

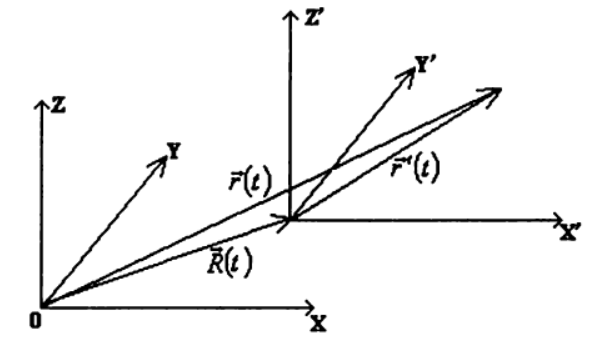
Таким образом, для нахождения закона движения точки в произвольной системе отсчета $inline$ необходимо:

1) задать закон движения точки — $\vec{r^{'}}(t)$ относительно системы отсчета $K^{'}$ ;
2) задать закон движения — $\vec{R}(t)$ системы отсчета $K^{'}$ относительно системы отсчета $inline$
3) определить закон движения точки — $\vec{r}(t)=\vec{r^{'}}(t)+\vec{R}(t)$ относительно системы отсчета $inline$ .

Построение орбиты Луны в гелиоцентрической системе отсчета

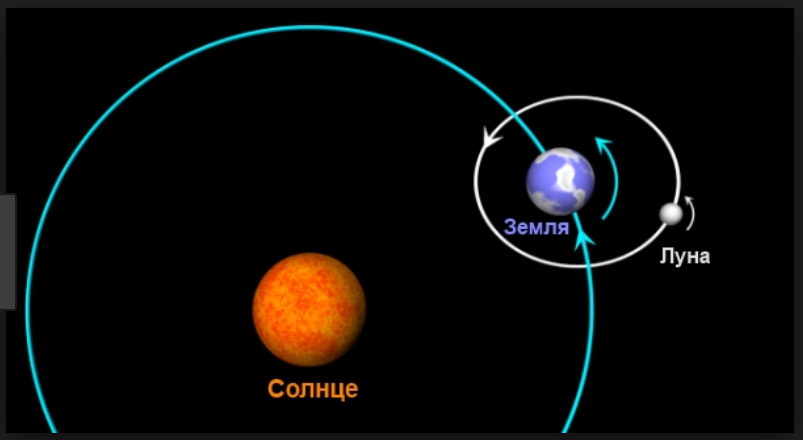
В гелиоцентрической системе отсчета (система $inline$ ) Земля движется по окружности радиуса
$R_{1}=1,496\cdot 10^{8}$ км (период обращения $Т_{1}=3,156\cdot 10^{7}$ с.). Луна, в свою очередь, движется вокруг Земли (система К') по окружности радиуса $R_{2}=3,844\cdot 10^{5}$ км. (период обращения $T_{2}=2,36\cdot 10^{6}$ с. Как известно [1,2], при движении материальной точки по окружности радиуса $inline$ с постоянной угловой скоростью $\omega$ координаты радиус-вектора, проведенного из начала координат к текущему положению точки, меняются по закону:

$\vec{R(t)}=\binom{R\cdot cos(\omega\cdot t+\varphi _{0})}{R\cdot sin(\omega\cdot t+\varphi _{0})}=\binom{R\cdot cos(\frac{2\pi }{T})+\varphi _{0})}{R\cdot sin(\frac{2\pi }{T}+\varphi _{0})},(3)$

где $\varphi _{0}$ — начальная фаза, характеризующая положение частицы в момент времени $inline$ , которую в дальнейшем мы будем полагать равной нулю. Заменяя в (3) $inline$ на $R_{1}$ и $R_{2}$ и подставляя в (1), получаем зависимость радиус-вектора Луны в гелиоцентрической системе координат от времени:

$\vec{r(t)}=\binom{x(t)}{y(t)}= \binom{R_{2}cos(\frac{2\pi }{T_{2}}t)+R_{1}cos(\frac{2\pi }{T_{1}}t)}{R_{2}sin(\frac{2\pi }{T_{2}}t)+R_{1}sin(\frac{2\pi }{T_{1}}t)},(4)$

Выражение (4) задает орбиту Луны ( $inline$ ) в параметрической форме, где параметром является время. Для построения искомой орбиты средствами Python, зададим радиусы орбит и периоды вращения Земли и Луны.

Земля движется в гелиоцентрической системе координат ( $inline$ ) её радиус орбиты и период обращения соответственно равны $R_{1}=1,496\cdot 10^{8} km,T_{1}=3,156\cdot 10^{7}s$ .Луна движется вокруг земли в системе координат ( $K^{'}$ ) её радиус орбиты и период обращения соответственно равны $R_{2}=3,844\cdot 10^{5} km,T_{2}=2,36\cdot 10^{6}s$ .

С учётом (4) определим функции зависимости координат от времени:

$\binom{(X(t)=R_{1}\cdot cos(\frac{2\pi }{T_{1}}\cdot t),Y(t)=R_{1}\cdot sin(\frac{2\pi }{T_{1}}\cdot t)}{x(t)=R_{2}\cdot cos(\frac{2\pi }{T_{2}}\cdot t),y(t)=R_{2}\cdot sin(\frac{2\pi }{T_{2}}\cdot t)},(5)$

Используя (5), получим пару координат для орбиты Луны:

$\binom{X_{g}(t)=X(t)+x(t)}{Y_{g}(t)=Y(t)+y(t)},(6)$

Зададим число точек, в которых вычисляются координаты N=1000 и дискретное время на интервале периода вращения Земли $dt=\frac{T_{1}}{N}$ . Напишем программу и построим график для положительной области изменения координат:

Определение орбит Земли и Луны

from numpy import*
from matplotlib.pyplot import*
R1=1.496*10**8#Числовые данные для расчётов взяты из  публикации [6]
T1=3.156*10**7
R2=3.844*10**5
T2=2.36*10**6
N=1000.0
def X(t):
         return R1*cos(2*pi*t/T1)
def Y(t):
         return R1*sin(2*pi*t/T1)
def x(t):
         return R2*cos(2*pi*t/T2)
def y(t):
         return R2*sin(2*pi*t/T2)
k=100
t=[T1*i/N for i in arange(0,k,1)]
X=array([X(w) for w in t])
Y=array([Y(w) for w in t])
x=array([x(w) for w in t])
y=array([y(w) for w in t])
XG=X+x
YG=Y+y
figure()
title("Траектория орбит Земли и Луны.\n Для положительных значений координат")
xlabel('$X(t_{k})$,$X_{g}(t_{k})$')
ylabel('$Y(t_{k})$,$Y_{g}(t_{k})$')
axis([1.2*10**8,1.5*10**8,0,1*10**8])
plot(X,Y,label='Орбита Земли')
plot(XG,YG,label='Орбита Луны')
legend(loc='best')
grid(True)
show()

Получим:

Рис.1

Созданный график позволяет расширить учебную задачу и посмотреть какой будет орбита луны, если радиус орбиты Луны будет равен $R_{2}=3,844\cdot 10^{7}$ .. Читателю, даже не имеющему специальных знаний по астрономии, понятно что Луна не может иметь такую орбиту в не поля тяготения Земли а гипотетический радиус используется для изучения условий возникновения петель. Внесём соответствующие изменения в программу:

Определение орбит Земли и Луны

изучения

 from numpy import*
from matplotlib.pyplot import*
R1=1.496*10**8#Числовые данные для расчётов взяты из  публикации [6]
T1=3.156*10**7
R2=3.844*10**7
T2=2.36*10**6
N=1000.0
def X(t):
         return R1*cos(2*pi*t/T1)
def Y(t):
         return R1*sin(2*pi*t/T1)
def x(t):
         return R2*cos(2*pi*t/T2)
def y(t):
         return R2*sin(2*pi*t/T2)
t=[T1*i/N for i in arange(0,N,1)]
X=array([X(w) for w in t])
Y=array([Y(w) for w in t])
x=array([x(w) for w in t])
y=array([y(w) for w in t])
XG=X+x
YG=Y+y
figure()
title("Гелиоцентрическая орбита  Земли и Луны")
xlabel('$X(t_{k})$,$X_{g}(t_{k})$')
ylabel('$Y(t_{k})$,$Y_{g}(t_{k})$')
axis([-2.0*10**8,2.0*10**8,-2.0*10**8,2.0*10**8])
plot(X,Y,label='Орбита Земли')
plot(XG,YG,label='Орбита Луны')
legend(loc='best')
grid(True)
show()

Получим:

Рис.2

Сравнивая орбиты Луны, представленные на рис. 1 и 2, обнаруживаем их существенные отличия. Для объяснения причины этих отличий необходимо сравнить линейные скорости движения Луны в первом и во втором случае и линейную скорость движения Земли.

Так как направление линейной скорости движения Земли относительно Солнца, как и направление линейной скорости движения Луны относительно Земли, меняется во времени, а скорость остается постоянной по величине.

В качестве количественной характеристики соотношения линейных скоростей движения Луны и Земли в гелиоцентрической системе координат следует выбрать разность между модулем линейной скорости движения Земли и проекцией линейной скорости Луны на направление вектора линейной скорости Земли:

$v_{o}(t)=\left | \vec{V}(t) \right |-\frac{(\vec{V}(t)\cdot \vec{v}(t))}{\left | \vec{V}(t) \right |},(7)$

Определим функции, описывающие законы изменения составляющих скорости Земли и Луны:

$\begin{matrix} V_{x}(t)=\frac{d}{dt}X(t),V_{y}(t)=\frac{d}{dt}Y(t) &\\ vx(t)=\frac{d}{dt}x(t),vy(t)=\frac{d}{dt}y(t) \end{matrix},(8)$

Чтобы определить результирующую скорость с учётом проекции, воспользуемся соотношением:

$D(t)=\sqrt{V_{x}(t)^{2}+V_{y}(t)^{2}}-\sqrt{vx(t)^{2}+vy(t)^{2}}\cdot \frac{V_{x}(t)\cdot vx(t)+V_{y}(t)\cdot vy(t)}{\sqrt{V_{x}(t)^{2}+V_{y}(t)^{2}}\cdot \sqrt{vx(t)^{2}+vy(t)^{2}}},(9)$

Напишем программу с учётом(5), (8), (9) и радиуса орбиты Луны $R_{2}=3,844\cdot 10^{5}$ км.:

Луна и Земля движутся в одном направлении

from numpy import*
from matplotlib.pyplot import*
R1=1.496*10**8#Числовые данные для расчётов взяты из  публикации [6]
T1=3.156*10**7
R2=3.844*10**5
T2=2.36*10**6
N=1000.0
k1=2*pi/T1
k2=2*pi/T2
def Vx(t):
         return -k1*R1*sin(k1*t)
def Vy(t):
         return k1*R1*cos(k1*t)
def vx(t):
         return -k2*R2*sin(k2*t)
def vy(t):
         return k2*R2*cos(k2*t)
def D(t):
         return sqrt(Vx(t)**2+Vy(t)**2)-sqrt(vx(t)**2+vy(t)**2)*(Vx(t)*vx(t)+Vy(t)*vy(t))/((sqrt(Vx(t)**2+Vy(t)**2))*(sqrt(vx(t)**2+vy(t)**2)))
x=[T1*i/N for i in arange(0,N,1)]
y=[D(t) for t in x]
title("Луна движется в  одном направлении с Землёй \n Радиус орбиты  Луны  R2=3.844*10**5 км.")
xlabel('t')
ylabel('D(t)')
plot(x,y)
show()

Получим:

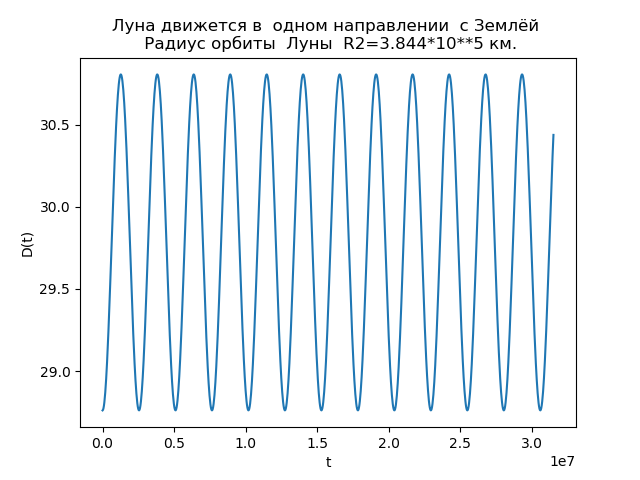
Рис.3.

Напишем программу с учётом (5), (8), (9) и радиуса орбиты Луны R2=3.844*10**7 км:

Луна периодически движется в противоположном к Земле направлению


from matplotlib.pyplot import*
R1=1.496*10**8#Числовые данные для расчётов взяты из  публикации [6]
T1=3.156*10**7
R2=3.844*10**7
T2=2.36*10**6
N=1000.0
k1=2*pi/T1
k2=2*pi/T2
def Vx(t):
         return -k1*R1*sin(k1*t)
def Vy(t):
         return k1*R1*cos(k1*t)
def vx(t):
         return -k2*R2*sin(k2*t)
def vy(t):
         return k2*R2*cos(k2*t)
def D(t):
         return sqrt(Vx(t)**2+Vy(t)**2)-sqrt(vx(t)**2+vy(t)**2)*(Vx(t)*vx(t)+Vy(t)*vy(t))/((sqrt(Vx(t)**2+Vy(t)**2))*(sqrt(vx(t)**2+vy(t)**2)))
x=[T1*i/N for i in arange(0,N,1)]
y=[D(t) for t in x]
title("  Периодически Луна движется в противоположном к Земле  \n направлению. Радиус орбиты  Луны  R2=3.844*10**7 км.")
xlabel('t')
ylabel('D(t)')
plot(x,y)
show()

Получим:

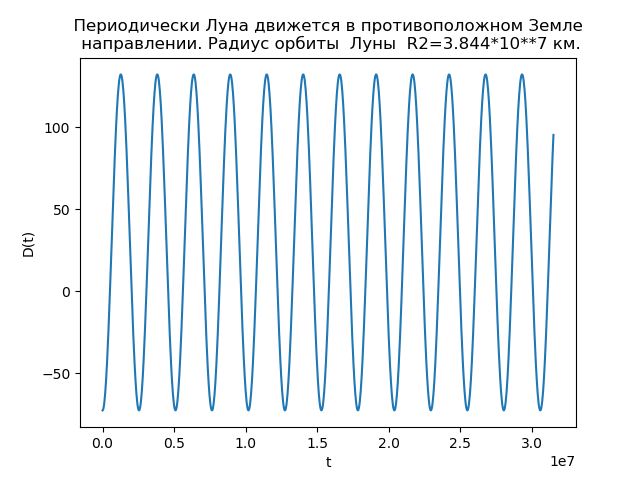
Рис.4.

Анализ зависимостей позволяет объяснить причину отличий орбит. Функция D(t) при $R_{2}=3,844\cdot 10^{5}$ км всегда положительна, т. е. Луна всегда движется в направлении движения Земли и петли не образуются. При $R_{2}=3,844\cdot 10^{7}$ км величина $inline$ принимает отрицательные значения, и существуют моменты времени, в которые Луна движется в направлении, противоположном направлению движения Земли, а потому орбита имеет петли.В этом и состоял смысл использования в расчётах не существующей орбиты Луны.

Построение орбиты Марса в системе отсчета, связанной с Землей

В гелиоцентрической системе отсчета (система К) Земля движется по окружности радиуса $R_{1}=1,496\cdot 10^{8}$ км, период обращения $T_{1}=365,24$ сут, Марс двигается по эллипсу, большая полуось которого $am=2,28\cdot 10^{8}$ км, период обращения Марса $T_{m}=689,98$ сут., эксцентриситет орбиты $inline$ [3]. Движение Земли описывается радиус-вектором R(t), задаваемым выражением (3). В связи с тем, что орбита Марса является эллипсом, зависимости $inline$ от времени задаются параметрически [4]:

$x(\varepsilon )=a_{m}\cdot(cos(\varepsilon) -e)$ , (10)

$y(\varepsilon )=a_{m}\cdot\sqrt{1-e^{2}}\cdot sin(\varepsilon)$ , (11)

$t(\varepsilon )=\frac{T_{m}}{2\pi }\cdot (\varepsilon-e\cdot sin(\varepsilon ) )$ , (12)

Полному обороту по эллипсу соответствует изменение параметра <img $\varepsilon$ от 0 до $2\pi$ . Для построения орбиты Марса необходимо вычислить в одни и те же моменты времени координаты радиус-векторов, описывающих положение Земли и Марса в гелиоцентрической системе отсчета, затем в соответствии с соотношением $\vec{r^{'}}(t)=\vec{r}(t)-\vec{R}(t)$ вычислить координаты Марса в системе отсчета, связанной с Землей.

Для построения орбиты Марса в системе отсчёта связанной с Землёй воспользуемся ранее приведенными параметрами орбит Земли и Марса, соотношениями (10)-(12), а также соотношениями для координат Земли:

$X(t)=R_{1}\cdot cos(\frac{2\pi }{T_{1}}t)$ , (13)

$Y(t)=R_{1}\cdot sin(\frac{2\pi }{T_{1}}t)$ ,(14)

Следует учесть, что число периодов обращения Марса вокруг Солнца равно $inline$ , тогда количество точек, в которых следует произвести расчёт и расстояние между ними, будут определяться из соотношений:

$N=4000\cdot K,\varepsilon_{i}=\frac{2\pi }{N}\cdot i,i=0...N$ (15)

Орбита Марса в системе отсчёта Земли

from numpy import*
from matplotlib.pyplot import*
R1=1.496*10e8#Числовые данные для расчётов взяты из  публикации [4]
T1=365.24
am=2.28*10e8
Tm=689.98
ee=0.093
N=36000
def x(g):
         return am*(cos(g)-ee)
def y(g):
         return am*sqrt(1-ee**2)*sin(g)
def t(g):
         return Tm*(g-ee*sin(g))/2*pi
def X(g):
         return R1*cos(2*pi*t(g)/T1)
def Y(g):
         return R1*sin(2*pi*t(g)/T1)
y=array([y(2*pi*i/N) for i in arange(0,N,1)])
x=array([x(2*pi*i/N) for i in arange(0,N,1)])
X=array([X(2*pi*i/N) for i in arange(0,N,1)])
Y=array([Y(2*pi*i/N) for i in arange(0,N,1)])
t=array([t(2*pi*i/N) for i in arange(0,N,1)])
figure()
title("Гелиоцентрические орбиты  Земли и Марса")
xlabel('x(g),X(g)')
ylabel('y(g),Y(g)')
plot(x,y,label='Орбита Марса')
plot(X,Y,label='Орбита Земли')
legend(loc='best')
figure()
title("Положение Марса в системе отсчёта связанной с Землёй")
xlabel('x1/10e8')
ylabel('y1(g/10e8')
x1=(x-X)
y1=(y-Y)
plot(x1/10e8,y1/10e8)
figure()
title("Зависимость расстояния между Землёй и Марсом \n от времени в годах")
xlabel('t/365.24')
ylabel('sqrt(x1**2+y1**2)/10e8')
y2=sqrt(x1**2+y1**2)/10e8
x2=t/365.24
plot(x2,y2)
show()

Получим:

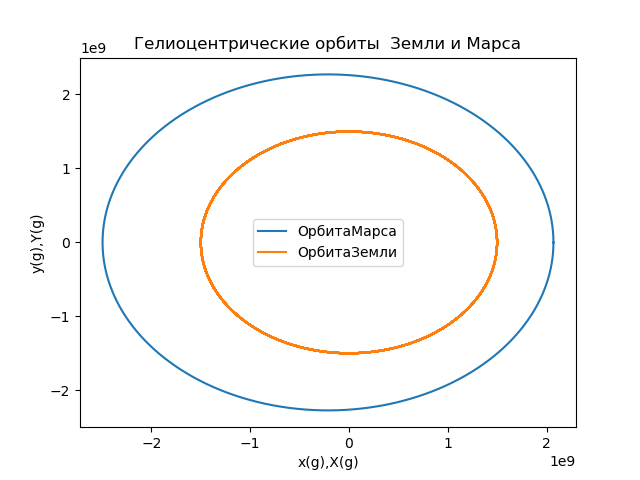
Рис.5

Вычислим координаты радиус-вектора, описывающего положение Марса в системе отсчета связанной с Землей, и построим орбиты (Рис.6), используя соотношение:

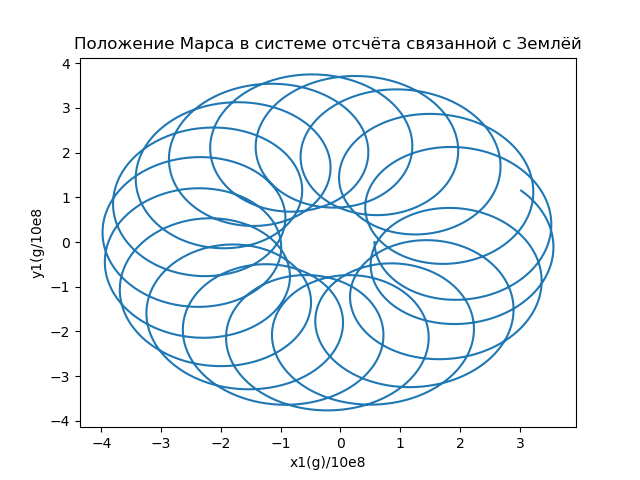
$x1_{i}=x(\varepsilon_{i})-X(t(\varepsilon_{i})),y1_{i}=y(\varepsilon_{i})-Y(t(\varepsilon_{i}))$ (16)

Рис.6

Еще одной важной характеристикой движения Марса (в первую очередь для межпланетных космических полетов) является расстояние между Землей и Марсом s(t), которое определяется модулем радиус-вектора, описывающего положение Марса в системе отсчета, связанной с Землей. Зависимость расстояния между Землей и Марсом от времени, измеряемого в земных годах, представлена на рис.7.

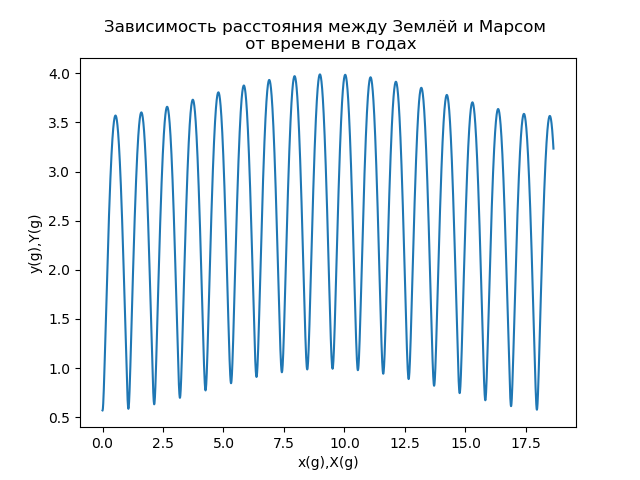
Рис.7

Анализ зависимости, представленной на рис.7, показывает, что расстояние между Землей и Марсом является сложной периодической функцией времени. Если воспользоваться терминологией теории сигналов [5], то о зависимости s(t) можно сказать, что она представляет собой амплитудно-модулированный сигнал, который принято представлять в виде произведения двух функций высокочастотной (несущей) и низкочастотной функции, задающей амплитудную модуляцию (огибающей):

$u(t)=(\bar{u}+a\cdot sin(\omega_{1}t))\cdot (1+\Delta a\cdot sin(\omega_{2}t))$ (17)

где $\bar{u}$ — постоянная составляющая функции $inline$ ; $inline$ — амплитуда сигнала; $\omega_{1}$ — частота несущей; $\Delta a$ — амплитуда функции, задающая глубину амплитудной модуляции; $\omega_{2}$ — частота модулирующей функции.

Из рис.7 видно, что период несущей составляет примерно 2 года, период модулирующей функции примерно 17 лет]6].

Построение гелиоцентрической орбиты кометы Галлея

В последний раз комета Галлея проходила через свой перигелий (ближайшая к Солнцу точка орбиты) 9 февраля 1986 года. (Само Солнце считается расположенным в начале координат.)

Координаты и компоненты скорости кометы Галлея в тот момент были равны $p_{0} = (0,325514, 0,459460, 0,166229)$ и $v_{0} = (–9,096111,–6,916686,–1,305721)$ соответственно, причем расстояние здесь выражено в астрономических единицах длины – а.е.д., или просто а.е. (астрономическая единица, т. е. длина большой главной полуоси земной орбиты), а время – в годах. В этих единицах измерения трехмерные уравнения движения кометы имеют вид:

$\left\{\begin{matrix} \frac{d^{2}x}{dt^{2}}=-\frac{\mu \cdot x}{r^{3}}\\ \frac{d^{2}y}{dt^{2}}=-\frac{\mu \cdot y}{r^{3}}\\ \frac{d^{2}z}{dt^{2}}=-\frac{\mu \cdot z}{r^{3}} \end{matrix}\right.,(18)$

(18)

где: $\mu =4\pi ^{2},r=\sqrt{x^{2}+y^{2}+z^{2}}$

Построение гелиоцентрической орбиты кометы Галлея

from numpy import*
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from matplotlib.patches import Circle  
def f(y, t):
         y1, y2, y3, y4,y5,y6 = y
         return [y2, -(4*pi*pi*y1)/(y1**2+y3**2 +y5**2)**(3/2),y4,-(4*pi*pi*y3)/(y1**2+y3**2 +y5**2)**(3/2),y6,-(4*pi*pi*y5)/(y1**2+y3**2 +y5**2)**(3/2)]  
t = linspace(0,300,10001)
y0 = [0.325514,-9.096111, -0.459460,-6.916686,0.166229,-1.305721]
[y1,y2, y3, y4,y5,y6]=odeint(f, y0, t, full_output=False).T
fig, ax = plt.subplots()
plt.title("Орбита кометы Галлея(расстояние в а.е., время в годах) \n Солнце в центре координат")
plt.xlabel('x(t)')
plt.ylabel('y(t)')
fig.set_facecolor('white')
ax.plot(y1,y3,linewidth=1)
circle = Circle((0, 0), 0.2, facecolor='orange')   
ax.add_patch(circle)
plt.axis([1,-21,-1,29])
plt.grid(True)
fig, ax = plt.subplots()
plt.title("Орбита кометы Галлея \n Солнце в центре координат")
plt.xlabel('x(t)')
plt.ylabel('z(t)')
fig.set_facecolor('white')
ax.plot(y1,y5,linewidth=1)
circle = Circle((0, 0), 0.1, facecolor='orange')   
ax.add_patch(circle)
plt.axis([1,-21,1,-11])
plt.grid(True)
fig, ax = plt.subplots()
plt.title("Орбита кометы Галлея \n Солнце в центре координат")
plt.xlabel('y(t)')
plt.ylabel('z(t)')
fig.set_facecolor('white')
ax.plot(y3,y5,linewidth=1)
circle = Circle((0, 0), 0.2, facecolor='orange')   
ax.add_patch(circle)
plt.axis([-1,29,1,-11])
plt.grid(True)
fig, ax = plt.subplots()
plt.title("Проекция скорости движения  кометы Галлея \n на плоскости ZOX и ZOY ")
ax.plot(t,y1,linewidth=1)
ax.plot(t,y3,linewidth=1)
plt.show()

Получим:

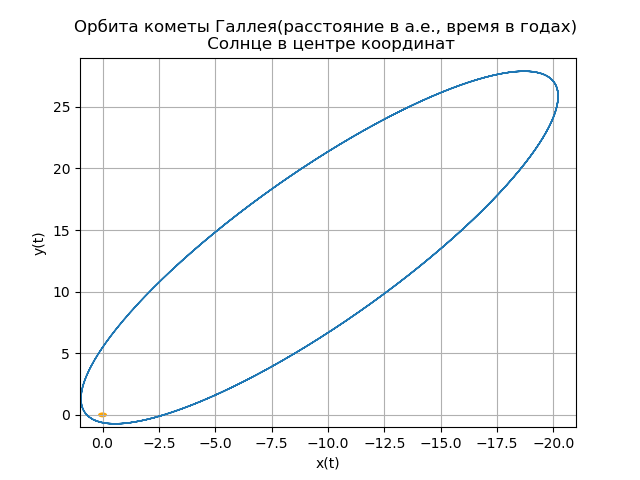
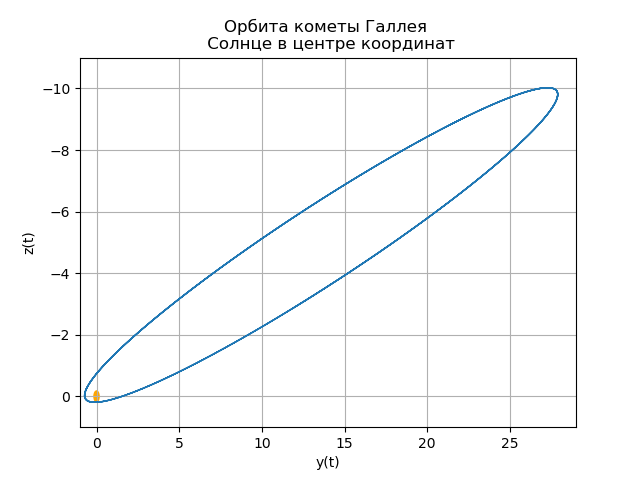
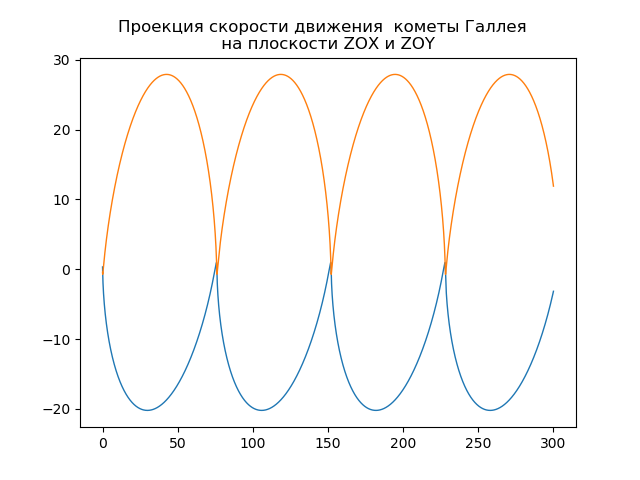
Ваша собственная комета

Попробуйте провести эксперимент. В ночь вы установите свой телескоп на вершине, недалеко расположенной от вашего дома возвышенности. Ночь должна быть ясной, безоблачной, звездной и, если вам улыбнулась фортуна: в 0 часов 30 минут ночи вы заметите новую комету.

После повторных наблюдений в следующие ночи вам удастся вычислить ее координаты в ту первую ночь. Координаты в гелиоцентрической системе координат: P0= (x0, y0, z0) и и вектор скорости v0 = (vx0, vy0, vz0).

Используя эти данные, определите:

расстояние кометы от Солнца в перигелии (самая близкая к Солнцу точка орбиты) и в афелии (самая дальняя от Солнца точка орбиты);
скорости кометы при прохождении через перигелий и через афелий;
период обращения кометы вокруг Солнца;
следующие две даты прохождения кометы через перигелий.

Если измерять расстояние в астрономических единицах, а время — в годах, то уравнение движения кометы примут вид (18). Для вашей собственной кометы выберите произвольные начальные координаты и скорости того же порядка, что и у кометы Галлея.

В случае необходимости, повторно осуществляйте произвольный выбор начального положения и вектора скорости до тех пор, пока не получите правдоподобную эксцентрическую орбиту, выходящую за пределы орбиты Земли (как у большинства настоящих комет).

Ссылки:

Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. 3-е изд. Т. 1.-2. М.: Мир, 1977.
Матвеев А. Н. Механики и теория относительности. М.: Высш. шк., 1986.
Физическая энциклопедия. Т. 3. М.: Большая российская энциклопедия, 1992.
Ландау Л. Д., Лифшиц Е. М. Курс теоретической физики. Механика. М.: Фю-матгиз, 1958.
Баскаков С. И. Радиотехнические цепи и сигналы. М.: Высш. шк., 1988.
Поршнев C.В. Компьютерное моделирование физических процессов с использованием пакета mathcad.

Теги:

Хабы:

Построение орбит небесных тел средствами Python

Системы отсчёта для определения орбиты

Построение орбиты Луны в гелиоцентрической системе отсчета

Построение орбиты Марса в системе отсчета, связанной с Землей

Построение гелиоцентрической орбиты кометы Галлея

Ссылки:

Публикации

Истории

Работа

Ближайшие события