Пришли очередные выходные, надо написать пару десятков строк кода и нарисовать картинку, да лучше не одну. Итак, на прошлых и позапрошлых выходных я показал, как делать трассировку лучей и даже взрывать всякое. Это многих удивляет, но комьпютерная графика — очень простая вещь, пары сотен строк голого C++ вполне хватает на создание интересных картинок.
Тема сегдоняшнего разговора — бинокулярное зрение, причём сегодня даже до ста строк кода не дотянем. Умея рендерить трёхмерные сцены, было бы глупо пройти мимо стерепар, сегодня будем рисовать примерно вот такое:

Безумие разработчиков Magic Carpet не даёт мне покоя. Для тех, кто не застал, эта игра позволяла делать 3Д рендер и в анаглиф, и в стереограммы в основных настройках, просто доступных в меню! Мозг это взрывало просто конкретно.
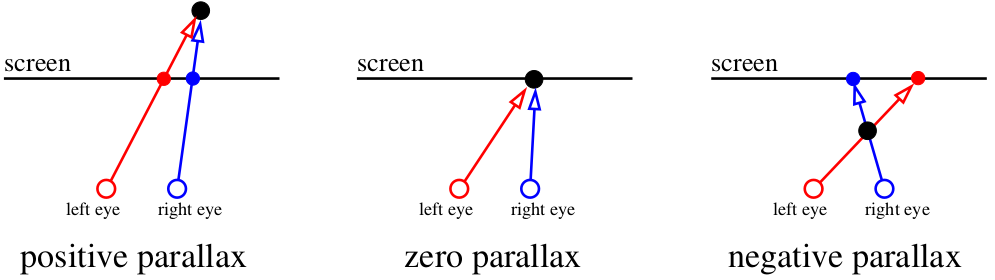
Итак, приступим. Для начала, благодаря чему вообще наш зрительный аппарат позволяет воспринимать глубину? Есть такое умное слово «параллакс». Если на пальцах, то давайте сфокусируем взгляд на экране. Всё, что находится в плоскости экрана, для нашего мозга существует в единичном экземпляре. А вот если вдруг муха пролетит перед экраном, то (если мы не меняем взгляда!) наш мозг её зарегистрирует в двух экземплярах. А заодно и паук на стене за экраном тоже раздваивается, причём направление раздвоения зависит от того, находится объект перед точкой фокуса или позади:

Наш мозг — это очень эффективная машина для анализа слегка отличающихся изображений. Он использует диспаратность для получения информации о глубине из двумерных изображений сетчатки для стереопсиса. Ну да бог с ними, со словами, давайте лучше картинки рисовать!
Давайте преставим, что наш экран — это окно в виртуальный мир :)

Наша задача — нарисовать две картинки с тем, что будет видно через это «окно». Картинок будет две, по одной на каждый глаз, на схеме выше я их показал красно-синим «бутербродом». Давайте пока не будем заморачиваться, как именно мы скормим эти картинки зрительному аппарату, нам нужно просто сохранить два файла. Конкретно меня интересует, как эти изображения можно получить при помощи нашего трассировщика лучей.
Ну, положим, направление взляда не меняется, это вектор (0,0,-1). Допустим, положение камеры мы можем сдвинуть на межглазное расстояние, что же ещё? Есть одна маленькая тонкость: конус взгляда через наше «окно» несимметричен. А наш рейтрейсер умеет рендерить только симметричный конус взгляда:

Что же делать? Читить :)
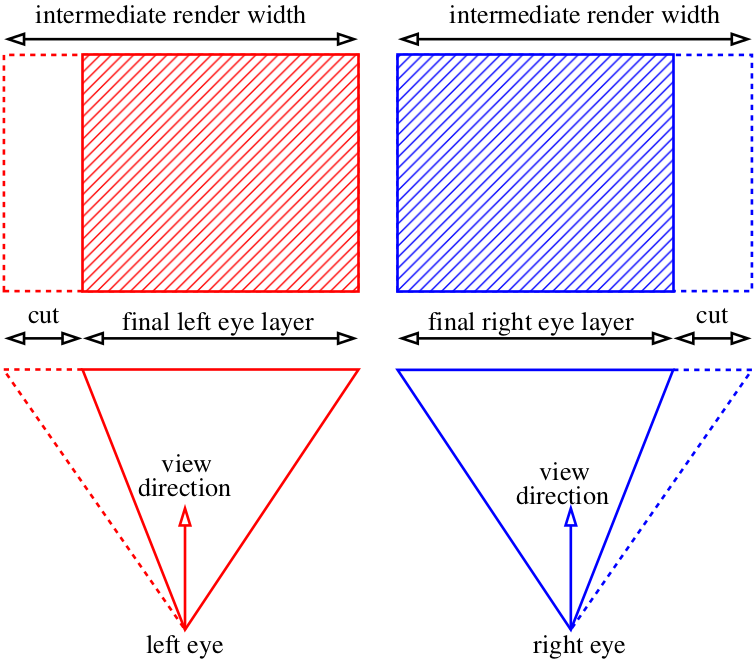
На самом деле, мы можем отрендерить картинки шире, нежели нам нужно, и просто обрезать лишнее:

С общим механизмом рендеринга должно быть понятно, теперь самое время задаться вопросом доставки изображения до нашего мозга. Один из самых простых вариантов это красно-синие очки:

Мы просто сделаем два пре-рендера не цветными, а чёрно-белыми, левую картинку запишем в красный канал, а правую — в синий. Получится вот такая картинка:

Красное стекло отрежет один канал, а синее стекло отрежет другой, таким образом, глаза получат каждый свою картинку, и мы можем посмотреть на мир в 3D. Вот тут изменения к основному комиту первой статьи, которые показывают и установки камеры для обоих глаз, и сборку каналов.
Анаглифные рендеры — один из самых древних способов просмотра (компьютерных!) стереокартинок. У них много недостатков, например, плохая цветопередача (кстати, попробуйте в зелёный канал финальной картинки записать зелёный канал правого глаза). Одна польза — такие очки легко сделать из подручных материалов.
С массовым распространением смартфонов мы вспомнили, что такое стереоскопы (которые, на секундочку, были изобретены в 19м веке)! Несколько лет назад гугл предложил использовать две копеечные линзы (к сожалению, на коленке не делаются), немного картона (валяется повсюду) и смартфон (лежит в кармане) для получения вполне сносных очков виртуальной реальности:

На алиэкспрессе их завались, сто рублей штука. По сравнению с анаглифом делать вообще ничего не надо, просто взять две картинки и составить их бок-о-бок, вот коммит.
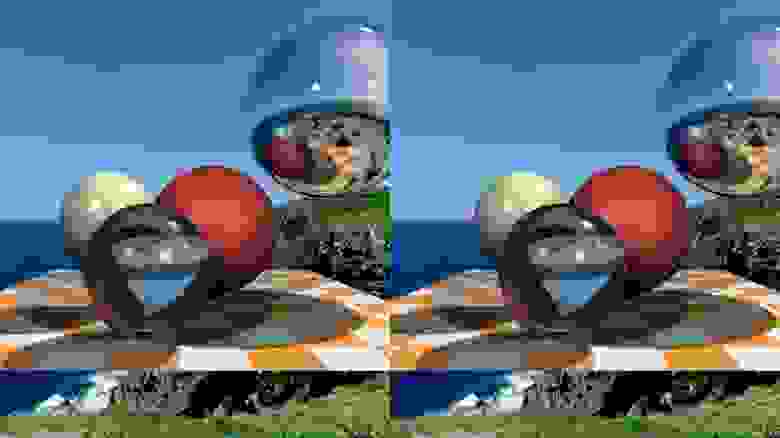
Строго говоря, в зависимости от линзы, может понадобиться коррекция искажения линзы, но я вообще не заморачивался, и на моих очках и так выглядит отлично. Но если очень нужно применить бочкообразное пред-искажение, которое компенсирует искажения от линзы, то вот вот так оно выглядит для моего смартфона и для моих очков:

А что же делать, если вообще не хочется использовать дополнительных приборов? Тогда вариант один — окосеть. Вообще говоря, предыдущей картинки вполне хватает для просмотра стерео, достаточно использовать трюк для просмотра стереограмм. Принципов просмотра стереограмм два: либо сдвигать глаза, либо раздвигать. Вот я нарисовал схему, на которой показываю, как можно смотреть на предыдущую картинку. Предыдущая картинка двойная, два красных штриха на схеме показывают два изображения на левой сетчатке, два синих — на правой.
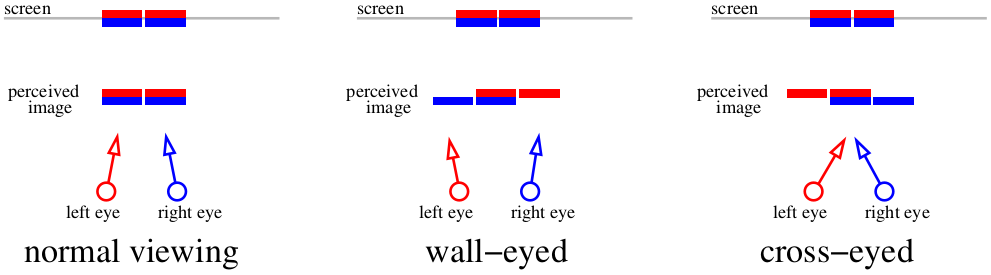
Если мы сфокусируем взгляд на экране, то из четырёх изображений у нас получится два. Если скосим глаза к носу, то вполне возможно показать мозгу «три» картинки. И наоборот, если раздвинуть глаза, то тоже можно получить «три» картинки. Наложение центральных картинок и даст мозгу стереоэффект.
Разным людям эти приёмы даются по-разному, я, например, совсем не умею глаза сдвигать, зато с лёгкостью развожу. Важно то, что стереограмма построенная для одного способа, должна этим же способом и просматриваться, иначе получается инвертированная карта глубин (см. отрицательный и положительный параллакс). Проблема такого способа просмотра стерео в том, что очень сложно сильно сдвинуть глаза относительно нормального состояния, поэтому приходится довольствоваться маленькими картинками. А что делать, если хочется больших? Давайте полностью пожертвуем цветом, и захотим получить только восприятие глубины. Забегая вперёд, вот картинка, которую мы получим в конце этой части:

Эта стереогрмма создана для «разведения» глаз (wall-eyed stereogram). Тем, кто предпочитает обратный способ просматривания, картинку брать тут. Если вы не привыкли к стереограммам, попробуйте разные условия: картинка на полный экран, маленькая картинка, яркий свет, темнота. Задача развести глаза так, чтобы две соседние вретикальные полоски совпали. Проще всего фокусироваться на левой верхней части картинки, т.к. она плоская. Мне, например, мешает окружение хабра, я открываю картинку на полный экран. Не забудьте с неё убрать мышку!
Не довольствуйтесь неполноценным 3D-эффектом. Если вы только смутно осознаёте округлые формы посреди случайных точек наряду с некоторыми слабыми 3D-эффектами, это, конечно, неполная иллюзия! Если смотреть правильно, шарики должны явно выйти из плоскости экрана на зрителя, эффект должен быть стабильным и сохраняться благодаря постоянному и детальному изучению каждой части изображения, как переднего плана, так и фона. У стереопсиса есть гистерезис: как только удаётся получить стабильное изображение, оно становится тем яснее, чем дольше вы смотрите. Чем дальше экран от глаз, тем больше эффект глубины.
Эта стереограмма нарисована по методу, предложенному четверть века назад Thimbleby и др. в их статье «Displaying 3D Images: Algorithms for Single Image Random Dot Stereograms».
Отправной точкой для отрисовки стереограмм является карта глубины (мы же забыли про цвет). Вот коммит, который рендерит вот такую картинку:

Глубины в нашем рендере обрезаны ближней и дальней плоскостями, то есть, самая дальняя точка в моей карте имеет глубину 0, самая ближняя 1.
Пусть у нас глаза находятся на расстоянии d от экрана. Поместим (воображаемую) дальнюю плоскость (z=0) на том же расстоянии позади экрана. Выберем постоянную μ, которая определит положение ближней плоскости (z=0): она будет на расстоянии μd от дальней. Я в своём коде выбрал μ=1/3. Итого, весь наш мир живёт на расстоянии от d-μd до d за экраном. Пусть у нас определено расстояние e между глазами (в пикселях, в моём коде я выбрал 400 пикселей).

Если мы смотрим на точку нашего объекта, отмеченную на схеме красным, то два пикселя, отмеченных зелёным, должны иметь одинаковый цвет в стереограмме. Как найти расстояние между этими пикселями? Очень просто. Если текущая проецируемая точка имеет глубину z, то отношение параллакса к расстоянию между глазами равно отношениям соответствующих глубин: p/e = (d-dμz)/(2d-dμz). Кстати, обратите внимание, что d сокращается и более нигде не участвует! То есть, p/e = (1-μz)/(2-μz), а это означает, что параллакс равняется p=e*(1-μz)/(2-μz) пикселей.
То есть, основной принцип построения стереограммы: мы проходим по всей карте глубины, для каждого значения глубины мы определяем, какие пиксели должны иметь одинаковый цвет, и записываем это в нашу систему ограничений. После чего стартуем с произвольной картинки, и стараемся выполнить все ранее наложенные ограничения.
В этом этапе мы подготовим картинку, на которую позже наложим ограничения параллакса.
Вот тут брать коммит, он рисует вот такую картинку:

Обратите внимание, что в целом цвета просто случайные, за исключением того, что я в красном канале положил rand()*sin, чтобы обеспечить периодические волны. Эти волны сделаны с расстоянием в 200 пикселей, это (при выбранных μ=1/3 и e=400) максимальное значение параллакса в нашем мире, оно же дальняя плоскость. Эти волны необязательны, но они облегчат нужную фокусировку зрения.
Собственно, полный код, относящийся к стереограмме, выглядит вот так:
Если что, то коммит брать тут. Функция int parallax(const float z) даёт расстояние между пикселями одинакового цвета для текущего значения глубины. Мы рендерим стереограмму построчно, так как строчки независимы между собой (у нас нет вертикального параллакса). Поэтому основной цикл просто пробегает все строчки; для каждой из них мы начинаем с полного неограниченного набора пикселей, на который затем будем накладывать попарные ограничения равенства, и в итоге у нас окажется некое количество кластеров (несвязных) пикселей одного цвета. Например, пиксель с индеком left и пиксель с индексом right должны в итоге оказаться одинаковыми.
Как хранить этот набор ограничений? Самый простой ответ — union–find data structure. Её я описывать не буду, это и так только три строчки кода, можно прочитать в википедии. Основная мысль в том, что для каждого кластера у нас окажется некий «ответственный» за него, он же коренной, пиксель, его мы оставим того цвета, какого он был в исходной картинке, а все остальные пиксели кластера перекрасим:
Ну, собственно, и всё. Двадцать строчек кода — и наша стереограмма готова, ломайте глаза и головы, рисуйте картинки! Кстати, просто случайные цвета в стереограмме — это вообще роскошь, в принципе, если постараться, то можно сделать и частичную передачу цвета нашей картинки.
Другие системы просмотра стерео, например, связанные с поляризацией, я вынес за рамки обсуждения, так как они выходят из бюджета ста рублей. Если что упустил, дополняйте и поправляйте!
Тема сегдоняшнего разговора — бинокулярное зрение, причём сегодня даже до ста строк кода не дотянем. Умея рендерить трёхмерные сцены, было бы глупо пройти мимо стерепар, сегодня будем рисовать примерно вот такое:

Безумие разработчиков Magic Carpet не даёт мне покоя. Для тех, кто не застал, эта игра позволяла делать 3Д рендер и в анаглиф, и в стереограммы в основных настройках, просто доступных в меню! Мозг это взрывало просто конкретно.
Параллакс
Итак, приступим. Для начала, благодаря чему вообще наш зрительный аппарат позволяет воспринимать глубину? Есть такое умное слово «параллакс». Если на пальцах, то давайте сфокусируем взгляд на экране. Всё, что находится в плоскости экрана, для нашего мозга существует в единичном экземпляре. А вот если вдруг муха пролетит перед экраном, то (если мы не меняем взгляда!) наш мозг её зарегистрирует в двух экземплярах. А заодно и паук на стене за экраном тоже раздваивается, причём направление раздвоения зависит от того, находится объект перед точкой фокуса или позади:
Наш мозг — это очень эффективная машина для анализа слегка отличающихся изображений. Он использует диспаратность для получения информации о глубине из двумерных изображений сетчатки для стереопсиса. Ну да бог с ними, со словами, давайте лучше картинки рисовать!
Давайте преставим, что наш экран — это окно в виртуальный мир :)
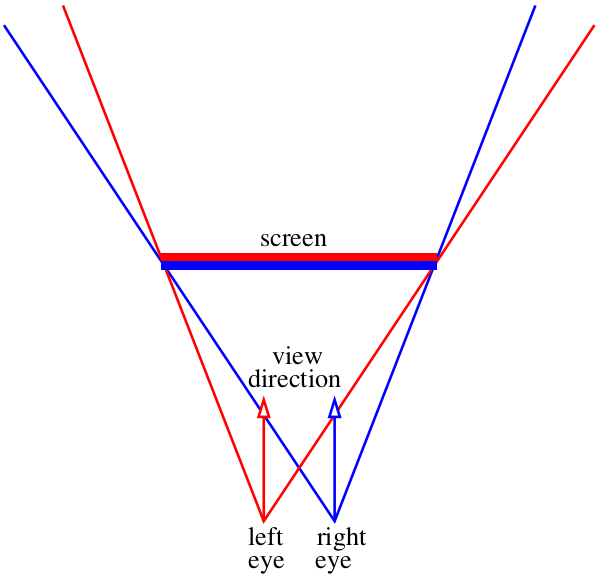
Наша задача — нарисовать две картинки с тем, что будет видно через это «окно». Картинок будет две, по одной на каждый глаз, на схеме выше я их показал красно-синим «бутербродом». Давайте пока не будем заморачиваться, как именно мы скормим эти картинки зрительному аппарату, нам нужно просто сохранить два файла. Конкретно меня интересует, как эти изображения можно получить при помощи нашего трассировщика лучей.
Ну, положим, направление взляда не меняется, это вектор (0,0,-1). Допустим, положение камеры мы можем сдвинуть на межглазное расстояние, что же ещё? Есть одна маленькая тонкость: конус взгляда через наше «окно» несимметричен. А наш рейтрейсер умеет рендерить только симметричный конус взгляда:
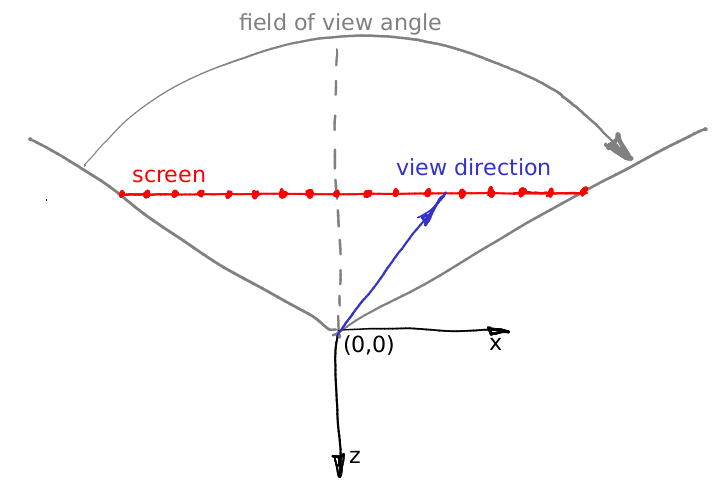
Что же делать? Читить :)
На самом деле, мы можем отрендерить картинки шире, нежели нам нужно, и просто обрезать лишнее:
Анаглиф
С общим механизмом рендеринга должно быть понятно, теперь самое время задаться вопросом доставки изображения до нашего мозга. Один из самых простых вариантов это красно-синие очки:

Мы просто сделаем два пре-рендера не цветными, а чёрно-белыми, левую картинку запишем в красный канал, а правую — в синий. Получится вот такая картинка:

Красное стекло отрежет один канал, а синее стекло отрежет другой, таким образом, глаза получат каждый свою картинку, и мы можем посмотреть на мир в 3D. Вот тут изменения к основному комиту первой статьи, которые показывают и установки камеры для обоих глаз, и сборку каналов.
Анаглифные рендеры — один из самых древних способов просмотра (компьютерных!) стереокартинок. У них много недостатков, например, плохая цветопередача (кстати, попробуйте в зелёный канал финальной картинки записать зелёный канал правого глаза). Одна польза — такие очки легко сделать из подручных материалов.
Стереоскоп
С массовым распространением смартфонов мы вспомнили, что такое стереоскопы (которые, на секундочку, были изобретены в 19м веке)! Несколько лет назад гугл предложил использовать две копеечные линзы (к сожалению, на коленке не делаются), немного картона (валяется повсюду) и смартфон (лежит в кармане) для получения вполне сносных очков виртуальной реальности:

На алиэкспрессе их завались, сто рублей штука. По сравнению с анаглифом делать вообще ничего не надо, просто взять две картинки и составить их бок-о-бок, вот коммит.

Строго говоря, в зависимости от линзы, может понадобиться коррекция искажения линзы, но я вообще не заморачивался, и на моих очках и так выглядит отлично. Но если очень нужно применить бочкообразное пред-искажение, которое компенсирует искажения от линзы, то вот вот так оно выглядит для моего смартфона и для моих очков:

Стереограммы
А что же делать, если вообще не хочется использовать дополнительных приборов? Тогда вариант один — окосеть. Вообще говоря, предыдущей картинки вполне хватает для просмотра стерео, достаточно использовать трюк для просмотра стереограмм. Принципов просмотра стереограмм два: либо сдвигать глаза, либо раздвигать. Вот я нарисовал схему, на которой показываю, как можно смотреть на предыдущую картинку. Предыдущая картинка двойная, два красных штриха на схеме показывают два изображения на левой сетчатке, два синих — на правой.
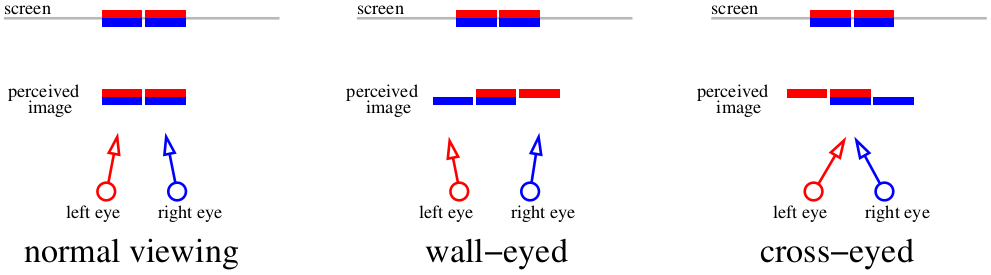
Если мы сфокусируем взгляд на экране, то из четырёх изображений у нас получится два. Если скосим глаза к носу, то вполне возможно показать мозгу «три» картинки. И наоборот, если раздвинуть глаза, то тоже можно получить «три» картинки. Наложение центральных картинок и даст мозгу стереоэффект.
Разным людям эти приёмы даются по-разному, я, например, совсем не умею глаза сдвигать, зато с лёгкостью развожу. Важно то, что стереограмма построенная для одного способа, должна этим же способом и просматриваться, иначе получается инвертированная карта глубин (см. отрицательный и положительный параллакс). Проблема такого способа просмотра стерео в том, что очень сложно сильно сдвинуть глаза относительно нормального состояния, поэтому приходится довольствоваться маленькими картинками. А что делать, если хочется больших? Давайте полностью пожертвуем цветом, и захотим получить только восприятие глубины. Забегая вперёд, вот картинка, которую мы получим в конце этой части:

Эта стереогрмма создана для «разведения» глаз (wall-eyed stereogram). Тем, кто предпочитает обратный способ просматривания, картинку брать тут. Если вы не привыкли к стереограммам, попробуйте разные условия: картинка на полный экран, маленькая картинка, яркий свет, темнота. Задача развести глаза так, чтобы две соседние вретикальные полоски совпали. Проще всего фокусироваться на левой верхней части картинки, т.к. она плоская. Мне, например, мешает окружение хабра, я открываю картинку на полный экран. Не забудьте с неё убрать мышку!
Не довольствуйтесь неполноценным 3D-эффектом. Если вы только смутно осознаёте округлые формы посреди случайных точек наряду с некоторыми слабыми 3D-эффектами, это, конечно, неполная иллюзия! Если смотреть правильно, шарики должны явно выйти из плоскости экрана на зрителя, эффект должен быть стабильным и сохраняться благодаря постоянному и детальному изучению каждой части изображения, как переднего плана, так и фона. У стереопсиса есть гистерезис: как только удаётся получить стабильное изображение, оно становится тем яснее, чем дольше вы смотрите. Чем дальше экран от глаз, тем больше эффект глубины.
Эта стереограмма нарисована по методу, предложенному четверть века назад Thimbleby и др. в их статье «Displaying 3D Images: Algorithms for Single Image Random Dot Stereograms».
Отправная точка
Отправной точкой для отрисовки стереограмм является карта глубины (мы же забыли про цвет). Вот коммит, который рендерит вот такую картинку:

Глубины в нашем рендере обрезаны ближней и дальней плоскостями, то есть, самая дальняя точка в моей карте имеет глубину 0, самая ближняя 1.
Основной принцип
Пусть у нас глаза находятся на расстоянии d от экрана. Поместим (воображаемую) дальнюю плоскость (z=0) на том же расстоянии позади экрана. Выберем постоянную μ, которая определит положение ближней плоскости (z=0): она будет на расстоянии μd от дальней. Я в своём коде выбрал μ=1/3. Итого, весь наш мир живёт на расстоянии от d-μd до d за экраном. Пусть у нас определено расстояние e между глазами (в пикселях, в моём коде я выбрал 400 пикселей).
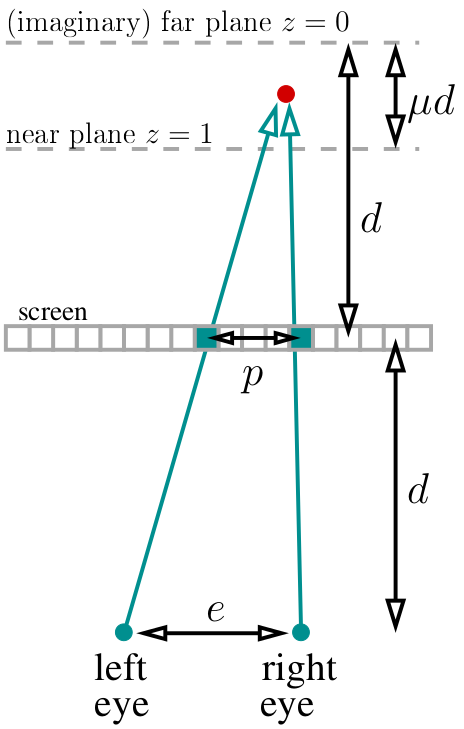
Если мы смотрим на точку нашего объекта, отмеченную на схеме красным, то два пикселя, отмеченных зелёным, должны иметь одинаковый цвет в стереограмме. Как найти расстояние между этими пикселями? Очень просто. Если текущая проецируемая точка имеет глубину z, то отношение параллакса к расстоянию между глазами равно отношениям соответствующих глубин: p/e = (d-dμz)/(2d-dμz). Кстати, обратите внимание, что d сокращается и более нигде не участвует! То есть, p/e = (1-μz)/(2-μz), а это означает, что параллакс равняется p=e*(1-μz)/(2-μz) пикселей.
То есть, основной принцип построения стереограммы: мы проходим по всей карте глубины, для каждого значения глубины мы определяем, какие пиксели должны иметь одинаковый цвет, и записываем это в нашу систему ограничений. После чего стартуем с произвольной картинки, и стараемся выполнить все ранее наложенные ограничения.
Подготавливаем исходную картинку
В этом этапе мы подготовим картинку, на которую позже наложим ограничения параллакса.
Вот тут брать коммит, он рисует вот такую картинку:

Обратите внимание, что в целом цвета просто случайные, за исключением того, что я в красном канале положил rand()*sin, чтобы обеспечить периодические волны. Эти волны сделаны с расстоянием в 200 пикселей, это (при выбранных μ=1/3 и e=400) максимальное значение параллакса в нашем мире, оно же дальняя плоскость. Эти волны необязательны, но они облегчат нужную фокусировку зрения.
Рендерим стереограмму
Собственно, полный код, относящийся к стереограмме, выглядит вот так:
int parallax(const float z) {
const float eye_separation = 400.; // interpupillary distance in pixels
const float mu = .33; // if the far plane is a distance D behind the screen, then the near plane is a distance mu*D in front of the far plane
return static_cast<int>(eye_separation*((1.-z*mu)/(2.-z*mu))+.5);
}
size_t uf_find(std::vector<size_t> &same, size_t x) {
return same[x]==x ? x : uf_find(same, same[x]);
}
void uf_union(std::vector<size_t> &same, size_t x, size_t y) {
if ((x=uf_find(same, x)) != (y=uf_find(same, y))) same[x] = y;
}
int main() {
[...]
for (size_t j=0; j<height; j++) { // autostereogram rendering loop
std::vector<size_t> same(width);
std::iota(same.begin(), same.end(), 0); // initialize the union-find data structure (same[i]=i)
for (size_t i=0; i<width; i++) { // put the constraints
int par = parallax(zbuffer[i+j*width]);
int left = i - par/2;
int right = left + par; // works better than i+par/2 for odd values of par
if (left>=0 && right<(int)width)
uf_union(same, left, right); // left and right pixels will have the same color
}
for (size_t i=0; i<width; i++) { // resolve the constraints
size_t root = uf_find(same, i);
for (size_t c=0; c<3; c++)
framebuffer[(i+j*width)*3+c] = framebuffer[(root+j*width)*3+c];
}
}
[...]
Если что, то коммит брать тут. Функция int parallax(const float z) даёт расстояние между пикселями одинакового цвета для текущего значения глубины. Мы рендерим стереограмму построчно, так как строчки независимы между собой (у нас нет вертикального параллакса). Поэтому основной цикл просто пробегает все строчки; для каждой из них мы начинаем с полного неограниченного набора пикселей, на который затем будем накладывать попарные ограничения равенства, и в итоге у нас окажется некое количество кластеров (несвязных) пикселей одного цвета. Например, пиксель с индеком left и пиксель с индексом right должны в итоге оказаться одинаковыми.
Как хранить этот набор ограничений? Самый простой ответ — union–find data structure. Её я описывать не буду, это и так только три строчки кода, можно прочитать в википедии. Основная мысль в том, что для каждого кластера у нас окажется некий «ответственный» за него, он же коренной, пиксель, его мы оставим того цвета, какого он был в исходной картинке, а все остальные пиксели кластера перекрасим:
for (size_t i=0; i<width; i++) { // resolve the constraints
size_t root = uf_find(same, i);
for (size_t c=0; c<3; c++)
framebuffer[(i+j*width)*3+c] = framebuffer[(root+j*width)*3+c];
}
Заключение
Ну, собственно, и всё. Двадцать строчек кода — и наша стереограмма готова, ломайте глаза и головы, рисуйте картинки! Кстати, просто случайные цвета в стереограмме — это вообще роскошь, в принципе, если постараться, то можно сделать и частичную передачу цвета нашей картинки.
Другие системы просмотра стерео, например, связанные с поляризацией, я вынес за рамки обсуждения, так как они выходят из бюджета ста рублей. Если что упустил, дополняйте и поправляйте!






