Введение:
Большое число самых разнообразных задач, относящихся практически ко всем важнейшим разделам математической физики и призванных ответить на актуальные технические вопросы, связано с применением функций Бесселя.
Функции Бесселя широко используются при решении задач акустики, радиофизики, гидродинамики, задач атомной и ядерной физики. Многочисленные приложения функций Бесселя к теории теплопроводности и теории упругости (задачи о колебаниях пластинок, задачи теории оболочек, задачи определения концентрации напряжения вблизи трещин).
Такая популярность функций Бесселя объясняется тем, что решение уравнений математической физики, содержащих оператор Лапласа в цилиндрических координатах, классическим методом разделения переменных приводит к обыкновенному дифференциальному уравнению, служащему для определения этих функций[1].
Функции Бесселя названы по имени немецкого астронома Фридриха Бесселя, который в работе 1824 года, изучая движение планет вокруг солнца, вывел рекуррентные соотношения для функций Бесселя , получил для целых
, получил для целых  интегральное представление функции
интегральное представление функции  , доказал наличие бесчисленного множества нулей функции
, доказал наличие бесчисленного множества нулей функции  и составил первые таблицы для функций
и составил первые таблицы для функций  и
и  .
.
Однако, впервые одна из функций Бесселя была рассмотрена еще в 1732 году Даниилом Бернулли в работе, посвященной колебанию тяжелых цепей. Д. Бернулли нашел выражение функции
была рассмотрена еще в 1732 году Даниилом Бернулли в работе, посвященной колебанию тяжелых цепей. Д. Бернулли нашел выражение функции  в виде степенного ряда и заметил (без доказательства), что уравнение
в виде степенного ряда и заметил (без доказательства), что уравнение  имеет бесчисленное множество действительных корней.
имеет бесчисленное множество действительных корней.
Следующей работой, в которой встречаются функции Бесселя, была работа Леонардо Эйлера 1738 года, посвященная изучению колебаний круглой мембраны. В этой работе Л. Эйлер нашел для целых выражение функции Бесселя
выражение функции Бесселя  в виде ряда по степеням
в виде ряда по степеням  , а в последующих работах распространил это выражение на случай произвольных значений индекса
, а в последующих работах распространил это выражение на случай произвольных значений индекса  . Кроме того, Л. Эйлер доказал, что для
. Кроме того, Л. Эйлер доказал, что для  , равного целому числу с половиной, функции
, равного целому числу с половиной, функции  выражаются через элементарные функции.
выражаются через элементарные функции.
Он заметил (без доказательства), что при действительных функции
функции  имеют бесчисленное множество действительных нулей и дал интегральное представление для
имеют бесчисленное множество действительных нулей и дал интегральное представление для  . Некоторые исследователи считают, что основные результаты, связанные с функциями Бесселя и их приложениями в математической физике, связаны с именем Л. Эйлера.
. Некоторые исследователи считают, что основные результаты, связанные с функциями Бесселя и их приложениями в математической физике, связаны с именем Л. Эйлера.
Изучить свойство функций Бесселя и одновременно освоить методы решения уравнений, сводящихся к функциям Бесселя, позволяет свободно распространяемая программа символьной математики SymPy — библиотеки Python.
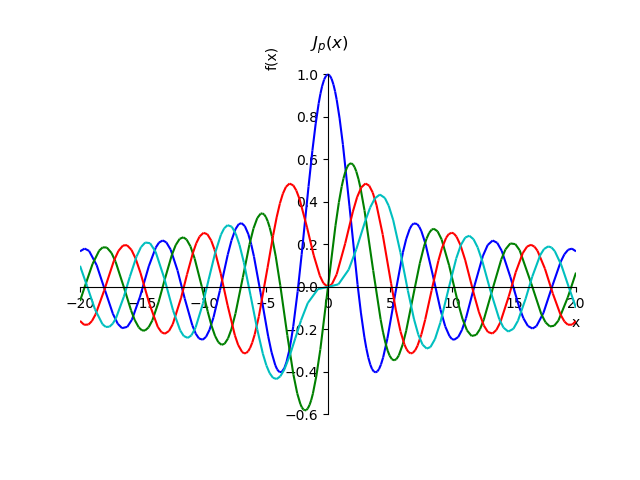
В программе символьной математики SymPy графики функций Бесселя первого рода целых порядков можно построить, пользуясь соотношением для суммы ряда:
При помощи соотношения для суммы ряда можно доказать свойство этих функций для целых порядков

Для демонстрации условий Коши, построим функцию и её производную
и её производную  :
:

Однако, для практических расчётов используется замечательный модуль mpmath, позволяющий численно не только решать уравнения с функциями Бесселя первого и второго рода в том числе и модифицированные всех допустимых порядков, но и строить графики с автоматическим масштабированием.
Кроме того, модуль mpmath не требует специальных средств для совместного использования символьной и численной математики. Историю создания этого модуля и возможности его использования для обратного преобразования Лапласа я уже рассматривал в публикации [2]. Теперь продолжим рассмотрение mpmath для работы с функциями Бесселя [3].
Функция Бесселя первого рода
mpmath.besselj(n, x, derivative=0) — дает функцию Бесселя первого рода . Функции
. Функции  является решением следующего дифференциального уравнения:
является решением следующего дифференциального уравнения:
Для целых положительных ведёт себя как синус или косинус, умноженный на коэффициент, который медленно убывает при
ведёт себя как синус или косинус, умноженный на коэффициент, который медленно убывает при 
Функция Бесселя первого рода является частным случаем гипергеометрической функции
является частным случаем гипергеометрической функции  :
:
Функцию Бесселя можно дифференцировать раз при условии, что m-я производная не равна нулю:
раз при условии, что m-я производная не равна нулю:
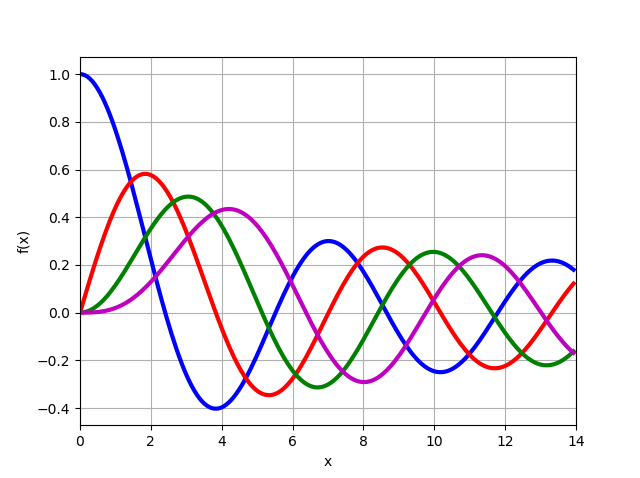
Функция Бесселя первого рода для положительных целых порядков n = 0,1,2,3 — решение уравнения Бесселя:
для положительных целых порядков n = 0,1,2,3 — решение уравнения Бесселя:
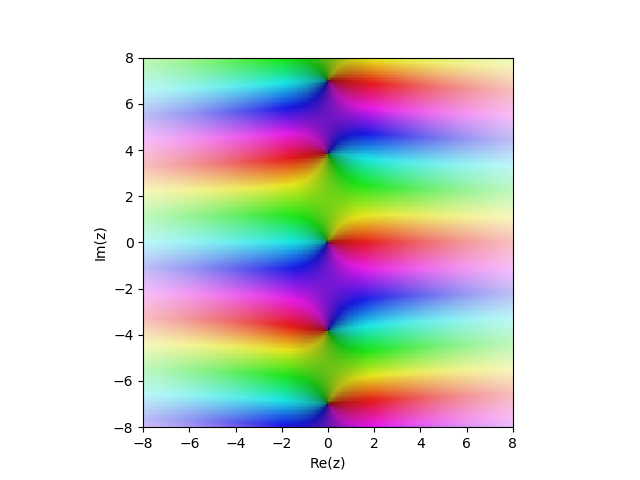
Функция Бесселя первого рода в комплексной плоскости:
в комплексной плоскости:

Примеры:
Функция обеспечивает результат с заданным числом цифр
обеспечивает результат с заданным числом цифр  после запятой:
после запятой:
Аргумент функции может быть большим числом:
Функции Бесселя первого рода удовлетворяют простым симметриям относительно :
:
Корни не периодические, но расстояние между последовательными корнями асимптотически приближается к . Функции Бесселя первого рода имеют следующий код:
. Функции Бесселя первого рода имеют следующий код:
Для или
или  функция Бесселя сводится к тригонометрической функции:
функция Бесселя сводится к тригонометрической функции:
Могут быть вычислены производные любого порядка, отрицательные порядки соответствуют интегрированию:
Дифференцирование с нецелым порядком дает дробную производную в смысле дифференциального интеграла Римана-Лиувилля, вычисляемую с помощью функции :
:
Другие способы вызова функции Бесселя первого рода нулевого и первого порядков
mpmath.j0(x) — Вычисляет функцию Бесселя ;
;
mpmath.j1(x) — Вычисляет функцию Бесселя ;
;
Функции Бесселя второго рода
bessely(n, x, derivative=0) Вычисляет функцию Бесселя второго рода по соотношению:
Для целого числа следующую формулу следует понимать как предел. Функцию Бесселя можно дифференцировать
следующую формулу следует понимать как предел. Функцию Бесселя можно дифференцировать  раз при условии, что m-я производная не равна нулю:
раз при условии, что m-я производная не равна нулю:

Функция Бесселя второго рода для целых положительных порядков
для целых положительных порядков  .
.

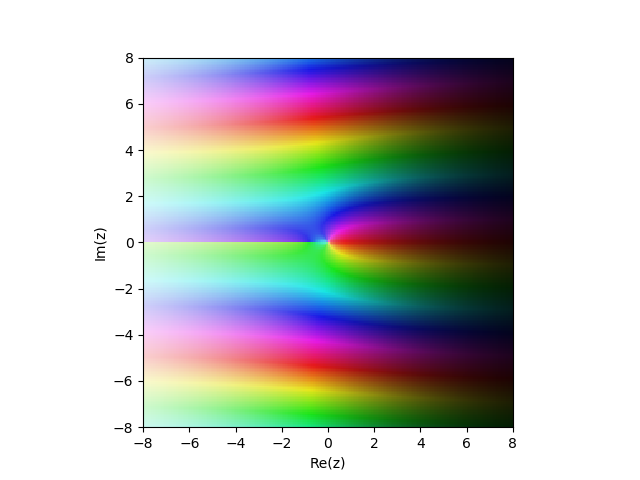
Функция Бесселя 2-го рода в комплексной плоскости
в комплексной плоскости

Примеры:
Некоторые значения функции :
:
Аргументы могут быть большими:
Производные любого порядка, в том числе и отрицательного, могут быть вычислены:
Модифицированная функция Бесселя первого рода
besseli(n, x, derivative=0) модифицированная функция Бесселя первого рода
Модифицированная функция Бесселя для вещественных порядков
для вещественных порядков  :
:

Модифицированная функция Бесселя в комплексной плоскости
в комплексной плоскости
Примеры:
Некоторые значения
Аргументы могут быть большими:
Для целых чисел n выполняется следующее интегральное представление:
Производные любого порядка могут быть вычислены:
Модифицированные функции Бесселя второго рода,
besselk(n, x) модифицированные функции Бесселя второго рода
Для целого числа эту формулу следует понимать как предел.
эту формулу следует понимать как предел.
Модифицированная функция Бесселя 2-го рода для вещественных
для вещественных  :
:

Модифицированная функция Бесселя 2-го рода в комплексной плоскости
в комплексной плоскости
Примеры:
Сложные и комплексные аргументы:
Аргументы – большие числа
Особенности поведения функции в точке :
:
Нули функции Бесселя
Для реального порядка и положительного целого числа
и положительного целого числа  возвращает
возвращает  , m-й положительный нуль функции Бесселя первого рода
, m-й положительный нуль функции Бесселя первого рода  (см. besselj ()). Альтернативно, с
(см. besselj ()). Альтернативно, с  , дает первый неотрицательный простой ноль
, дает первый неотрицательный простой ноль  из
из  . Обозначения по соглашению об индексации с использованием Abramowitz & Stegun и DLMF. Обратите внимание на особый случай
. Обозначения по соглашению об индексации с использованием Abramowitz & Stegun и DLMF. Обратите внимание на особый случай  , в то время как все остальные нули положительны.
, в то время как все остальные нули положительны.
В действительности подсчитываются только простые нули (все нули функций Бесселя простые, за исключением когда ), и
), и  становится монотонной функцией от
становится монотонной функцией от  и
и  . Нули чередуются согласно неравенствам:
. Нули чередуются согласно неравенствам:
Примеры:
Начальные нули функций Бесселя ,
, ,
,
Начальные нули производных от функций Бесселя ,
, ,
,
Нули с большим индексом:
Нули функций с большим порядком:
Нули функций с дробным порядком:
И . и
. и  можно выразить как бесконечные произведения по их нулям:
можно выразить как бесконечные произведения по их нулям:
Для реального порядка и положительного целого числа
и положительного целого числа  возвращает
возвращает  ,
,  , m-й положительный нуль функции Бесселя второго рода
, m-й положительный нуль функции Бесселя второго рода  (см. Bessely ()). Альтернативно, с
(см. Bessely ()). Альтернативно, с  , дает первый положительный нуль
, дает первый положительный нуль  из
из  . Нули чередуются согласно неравенствам:
. Нули чередуются согласно неравенствам:
Примеры:
Начальные нули функций Бесселя ,
, ,
,
Начальные нули производных от функций Бесселя ,
, ,
,
Нули с большим индексом:
Нули функций с большим порядком:
Нули функций с дробным порядком:
Приложения функций Бесселя
Важность функций Бесселя обусловлена не только частым появлением уравнения Бесселя в приложениях, но также и тем, что решения многих других линейных дифференциальных уравнений второго порядка могут быть выражены через функции Бесселя. Чтобы увидеть как они появляются, мы начнем с уравнения Бесселя порядка в форме:
в форме:
и подставим сюда
Тогда, используя (2) и введя константы из уравнения (1), получим:
из уравнения (1), получим:
Из уравнения (4) получим:
Если ,
,  ,
,  , то общее решение (для
, то общее решение (для  ) уравнения (3) имеет вид:
) уравнения (3) имеет вид:
где: ,
,  ,
,  определяются из системы (5). Если
определяются из системы (5). Если  — целое число, то
— целое число, то  нужно заменить на
нужно заменить на  .
.
Продольный изгиб вертикальной колонны
Мы теперь рассмотрим задачу, важную для практических приложений. В этой задаче требуется определить, когда однородная вертикальная колонна согнется под ее собственным весом. Мы полагаем в свободном верхнем конце колонны и
в свободном верхнем конце колонны и  в её основании; мы предполагаем, что основание жестко вставлено (т. е. закреплено неподвижно) в основу (в землю), возможно в бетон.
в её основании; мы предполагаем, что основание жестко вставлено (т. е. закреплено неподвижно) в основу (в землю), возможно в бетон.

Обозначим угловое отклонение колонны в точке через
через  . Из теории эластичности при данных условиях следует, что:
. Из теории эластичности при данных условиях следует, что:
где — модуль Юнга материала колонны,
— модуль Юнга материала колонны,  — момент инерции ее поперечного сечения,
— момент инерции ее поперечного сечения,  — линейная плотность колонны и
— линейная плотность колонны и  — гравитационное ускорение. Граничные условия имеют вид:
— гравитационное ускорение. Граничные условия имеют вид:
Будем решать задачу, используя (7) и (8) при:
Перепишем (7) с учётом (9) при условии (8):
Колонна может деформироваться, только если есть нетривиальное решение задачи (10); иначе колонна останется в не отклоненном от вертикали положении (т. е. физически не сможет отклониться от вертикали).
Дифференциальное уравнение (10) представляет собой уравнение Эйри. Уравнение (10) имеет форму уравнения (3) при ,
,  ,
,  . Из системы уравнений (5) получаем
. Из системы уравнений (5) получаем  ,
,  ,
,  ,
,  .
.
Поэтому общее решение имеет вид:
Чтобы применить начальные условия, мы подставляем в
в
После преобразования (12), с учётом решения (11), получим:
При условии в начальной точке , получим
, получим  , тогда (11) примет вид:
, тогда (11) примет вид:
При условии в конечной точке , из (14) получим:
, из (14) получим:
Следует отметить, что преобразований (13), (14) можно было не делать, если построить графики функций , воспользовавшись рассмотренными возможностями модуля mpmath:
, воспользовавшись рассмотренными возможностями модуля mpmath:

Из графика следует, что при x=0 функция и с учётом решения (11), мы сразу получаем необходимое уравнение (15), остаётся только найти z, как будет показано далее.
и с учётом решения (11), мы сразу получаем необходимое уравнение (15), остаётся только найти z, как будет показано далее.
Таким образом, колонна деформируется, только если — корень уравнения
— корень уравнения  . Построим функцию
. Построим функцию  на отдельном графике:
на отдельном графике:

На графике видно, что первый корень немного меньше 2. Найти корень из уравнения
из уравнения  можно, воспользовавшись функцией findroot(f, z0), приняв, согласно графика, точку поиска
можно, воспользовавшись функцией findroot(f, z0), приняв, согласно графика, точку поиска  и шесть знаков после запятой mp.dps = 6:
и шесть знаков после запятой mp.dps = 6:
Получим:

Рассчитаем критическую длину, например флагштока, по формуле (15):
Получим:
8.47 м
10.25 м
Полый флагшток может быть выше, чем сплошной.
Тонкая мембрана при попадании на неё звуковых волн не только колеблется с частотой волн. Форму колебаний мембраны можно получить в функциях Бесселя по следующему листингу, пользуясь формулами besselj() и besseljzero():
Не углубляясь в детальное рассмотрение функций Бесселя из библиотеки SciPy[4], приведу только два листинга для построения графиков функций первого и второго рода jv(v, x), yv(v, x):


В статье изложены основы работы с функциями Бесселя при помощи библиотек mpmath, sympy и scipy, приведены примеры применения функций для решения дифференциальных уравнений. Статья может быть полезна при изучении уравнений математической физики.
1.Функции Бесселя
2.Использование обратного преобразования Лапласа для анализа динамических звеньев систем управления
3.Bessel function related functions
4. Special functions (scipy.special).
Большое число самых разнообразных задач, относящихся практически ко всем важнейшим разделам математической физики и призванных ответить на актуальные технические вопросы, связано с применением функций Бесселя.
Функции Бесселя широко используются при решении задач акустики, радиофизики, гидродинамики, задач атомной и ядерной физики. Многочисленные приложения функций Бесселя к теории теплопроводности и теории упругости (задачи о колебаниях пластинок, задачи теории оболочек, задачи определения концентрации напряжения вблизи трещин).
Такая популярность функций Бесселя объясняется тем, что решение уравнений математической физики, содержащих оператор Лапласа в цилиндрических координатах, классическим методом разделения переменных приводит к обыкновенному дифференциальному уравнению, служащему для определения этих функций[1].
Функции Бесселя названы по имени немецкого астронома Фридриха Бесселя, который в работе 1824 года, изучая движение планет вокруг солнца, вывел рекуррентные соотношения для функций Бесселя
Однако, впервые одна из функций Бесселя
Следующей работой, в которой встречаются функции Бесселя, была работа Леонардо Эйлера 1738 года, посвященная изучению колебаний круглой мембраны. В этой работе Л. Эйлер нашел для целых
Он заметил (без доказательства), что при действительных
Изучить свойство функций Бесселя и одновременно освоить методы решения уравнений, сводящихся к функциям Бесселя, позволяет свободно распространяемая программа символьной математики SymPy — библиотеки Python.
В программе символьной математики SymPy графики функций Бесселя первого рода целых порядков можно построить, пользуясь соотношением для суммы ряда:
Функции Бесселя первого рода
from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{p}(x)" p1=plot(besselj(0,x),(x,-20,20),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(1,x),(x,-20,20),line_color='g',show=False) p3=plot(besselj(2,x),(x,-20,20),line_color='r',show=False) p4=plot(besselj(3,x),(x,-20,20),line_color='c',show=False) p1.extend(p2) p1.extend(p3) p1.extend(p4) p1.show()

При помощи соотношения для суммы ряда можно доказать свойство этих функций для целых порядков
Свойство функции Бесселя первого рода
from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1}(x)=-J_{-1}(x)" p1=plot(besselj(1,x),(x,-10,10),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(-1,x),(x,-10,10),line_color='r',show=False) p1.extend(p2) p1.show()

Для демонстрации условий Коши, построим функцию
Функция дробного порядка и её производная
from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1/3}(x),J{}'_{1/3}(x)" p1=plot(besselj(1/3,x),(x,-1,10),line_color='b',title=' $'+st+ '$',ylim=(-1,2),show=False) def dbesselj(p,x): return diff(summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]),x) p2=plot(dbesselj(1/3,x),(x,-1,10),line_color='g',show=False) p1.extend(p2) p1.show()

Однако, для практических расчётов используется замечательный модуль mpmath, позволяющий численно не только решать уравнения с функциями Бесселя первого и второго рода в том числе и модифицированные всех допустимых порядков, но и строить графики с автоматическим масштабированием.
Кроме того, модуль mpmath не требует специальных средств для совместного использования символьной и численной математики. Историю создания этого модуля и возможности его использования для обратного преобразования Лапласа я уже рассматривал в публикации [2]. Теперь продолжим рассмотрение mpmath для работы с функциями Бесселя [3].
Функция Бесселя первого рода
mpmath.besselj(n, x, derivative=0) — дает функцию Бесселя первого рода
Для целых положительных
Функция Бесселя первого рода
Функцию Бесселя можно дифференцировать
Функция Бесселя первого рода
from mpmath import* j0 = lambda x: besselj(0,x) j1 = lambda x: besselj(1,x) j2 = lambda x: besselj(2,x) j3 = lambda x: besselj(3,x) plot([j0,j1,j2,j3],[0,14]

Функция Бесселя первого рода
from sympy import* from mpmath import* cplot(lambda z: besselj(1,z), [-8,8], [-8,8], points=50000)

Примеры:
Функция
from mpmath import* mp.dps = 15; mp.pretty = True print(besselj(2, 1000)) nprint(besselj(4, 0.75)) nprint(besselj(2, 1000j)) mp.dps = 25 nprint( besselj(0.75j, 3+4j)) mp.dps = 50 nprint( besselj(1, pi))
Аргумент функции может быть большим числом:
from mpmath import* mp.dps = 25 nprint( besselj(0, 10000)) nprint(besselj(0, 10**10)) nprint(besselj(2, 10**100)) nprint( besselj(2, 10**5*j))
Функции Бесселя первого рода удовлетворяют простым симметриям относительно
from sympy import* from mpmath import* mp.dps = 15 nprint([besselj(n,0) for n in range(5)]) nprint([besselj(n,pi) for n in range(5)]) nprint([besselj(n,-pi) for n in range(5)])
Корни не периодические, но расстояние между последовательными корнями асимптотически приближается к
from mpmath import* print(quadosc(j0, [0, inf], period=2*pi)) print(quadosc(j1, [0, inf], period=2*pi))
Для
from sympy import* from mpmath import* x = 10 print(besselj(0.5, x)) print(sqrt(2/(pi*x))*sin(x)) print(besselj(-0.5, x)) print(sqrt(2/(pi*x))*cos(x))
Могут быть вычислены производные любого порядка, отрицательные порядки соответствуют интегрированию:
from mpmath import* mp.dps = 25 print(besselj(0, 7.5, 1)) print(diff(lambda x: besselj(0,x), 7.5)) print(besselj(0, 7.5, 10)) print(diff(lambda x: besselj(0,x), 7.5, 10)) print(besselj(0,7.5,-1) - besselj(0,3.5,-1)) print(quad(j0, [3.5, 7.5]))
Дифференцирование с нецелым порядком дает дробную производную в смысле дифференциального интеграла Римана-Лиувилля, вычисляемую с помощью функции
from mpmath import* mp.dps = 15 print(besselj(1, 3.5, 0.75)) print(differint(lambda x: besselj(1, x), 3.5, 0.75))
Другие способы вызова функции Бесселя первого рода нулевого и первого порядков
mpmath.j0(x) — Вычисляет функцию Бесселя
mpmath.j1(x) — Вычисляет функцию Бесселя
Функции Бесселя второго рода
bessely(n, x, derivative=0) Вычисляет функцию Бесселя второго рода по соотношению:
Для целого числа
Функция Бесселя второго рода
from sympy import* from mpmath import* y0 = lambda x: bessely(0,x) y1 = lambda x: bessely(1,x) y2 = lambda x: bessely(2,x) y3 = lambda x: bessely(3,x) plot([y0,y1,y2,y3],[0,10],[-4,1])

Функция Бесселя 2-го рода
from sympy import* from mpmath import* cplot(lambda z: bessely(1,z), [-8,8], [-8,8], points=50000)

Примеры:
Некоторые значения функции
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0,0)) print(bessely(1,0)) print(bessely(2,0)) print(bessely(1, pi)) print(bessely(0.5, 3+4j))
Аргументы могут быть большими:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0, 10000)) print(bessely(2.5, 10**50)) print(bessely(2.5, -10**50))
Производные любого порядка, в том числе и отрицательного, могут быть вычислены:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(2, 3.5, 1)) print(diff(lambda x: bessely(2, x), 3.5)) print(bessely(0.5, 3.5, 1)) print(diff(lambda x: bessely(0.5, x), 3.5)) print(diff(lambda x: bessely(2, x), 0.5, 10)) print(bessely(2, 0.5, 10)) print(bessely(2, 100.5, 100)) print(quad(lambda x: bessely(2,x), [1,3])) print(bessely(2,3,-1) - bessely(2,1,-1))
Модифицированная функция Бесселя первого рода
mpmath.besseli(n, x, derivative=0)
besseli(n, x, derivative=0) модифицированная функция Бесселя первого рода
Модифицированная функция Бесселя
from mpmath import* i0 = lambda x: besseli(0,x) i1 = lambda x: besseli(1,x) i2 = lambda x: besseli(2,x) i3 = lambda x: besseli(3,x) plot([i0,i1,i2,i3],[0,5],[0,5])

Модифицированная функция Бесселя
from mpmath import* cplot(lambda z: besseli(1,z), [-8,8], [-8,8], points=50000)

Примеры:
Некоторые значения
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(0,0)) print(besseli(1,0)) print(besseli(0,1)) print(besseli(3.5, 2+3j))
Аргументы могут быть большими:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 1000)) print(besseli(2, 10**10)) print(besseli(2, 6000+10000j))
Для целых чисел n выполняется следующее интегральное представление:
from mpmath import* mp.dps = 15; mp.pretty = True n = 3 x = 2.3 print(quad(lambda t: exp(x*cos(t))*cos(n*t), [0,pi])/pi) print(besseli(n,x))
Производные любого порядка могут быть вычислены:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 7.5, 1)) print(diff(lambda x: besseli(2,x), 7.5)) print(besseli(2, 7.5, 10)) print(diff(lambda x: besseli(2,x), 7.5, 10)) print(besseli(2,7.5,-1) - besseli(2,3.5,-1)) print(quad(lambda x: besseli(2,x), [3.5, 7.5]))
Модифицированные функции Бесселя второго рода,
mpmath.besselk(n, x)
besselk(n, x) модифицированные функции Бесселя второго рода
Для целого числа
Модифицированная функция Бесселя 2-го рода
from mpmath import* k0 = lambda x: besselk(0,x) k1 = lambda x: besselk(1,x) k2 = lambda x: besselk(2,x) k3 = lambda x: besselk(3,x) plot([k0,k1,k2,k3],[0,8],[0,5])

Модифицированная функция Бесселя 2-го рода
from mpmath import* cplot(lambda z: besselk(1,z), [-8,8], [-8,8], points=50000)

Примеры:
Сложные и комплексные аргументы:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0,1)) print(besselk(0, -1)) print(besselk(3.5, 2+3j)) print(besselk(2+3j, 0.5))
Аргументы – большие числа
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0, 100)) print(besselk(1, 10**6)) print(besselk(1, 10**6*j)) print(besselk(4.5, fmul(10**50, j, exact=True)))
Особенности поведения функции в точке
from mpmath import * print(besselk(0,0)) print(besselk(1,0)) for n in range(-4, 5): print(besselk(n, '1e-1000'))
Нули функции Бесселя
besseljzero() mpmath.besseljzero(v, m, derivative=0)
Для реального порядка
В действительности подсчитываются только простые нули (все нули функций Бесселя простые, за исключением когда
Примеры:
Начальные нули функций Бесселя
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1)) print(besseljzero(0,2)) print(besseljzero(0,3)) print(besseljzero(1,1)) print(besseljzero(1,2)) print(besseljzero(1,3)) print(besseljzero(2,1)) print(besseljzero(2,2)) print(besseljzero(2,3))
Начальные нули производных от функций Бесселя
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1,1)) print(besseljzero(0,2,1)) print(besseljzero(0,3,1)) print(besseljzero(1,1,1)) print(besseljzero(1,2,1)) print(besseljzero(1,3,1)) print(besseljzero(2,1,1)) print(besseljzero(2,2,1)) print(besseljzero(2,3,1))
Нули с большим индексом:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,100)) print(besseljzero(0,1000)) print(besseljzero(0,10000)) print(besseljzero(5,100)) print(besseljzero(5,1000)) print(besseljzero(5,10000)) print(besseljzero(0,100,1)) print(besseljzero(0,1000,1)) print(besseljzero(0,10000,1))
Нули функций с большим порядком:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(50,1)) print(besseljzero(50,2)) print(besseljzero(50,100)) print(besseljzero(50,1,1)) print(besseljzero(50,2,1)) print(besseljzero(50,100,1))
Нули функций с дробным порядком:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0.5,1)) print(besseljzero(1.5,1)) print(besseljzero(2.25,4))
И
from mpmath import * mp.dps = 6; mp.pretty = True v,z = 2, mpf(1) nprint((z/2)**v/gamma(v+1) * \ nprod(lambda k: 1-(z/besseljzero(v,k))**2, [1,inf])) print(besselj(v,z)) nprint((z/2)**(v-1)/2/gamma(v) * \ nprod(lambda k: 1-(z/besseljzero(v,k,1))**2, [1,inf])) print(besselj(v,z,1))
besselyzero() mpmath.besselyzero(v, m, derivative=0)
Для реального порядка
Примеры:
Начальные нули функций Бесселя
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1)) print(besselyzero(0,2)) print(besselyzero(0,3)) print(besselyzero(1,1)) print(besselyzero(1,2)) print(besselyzero(1,3)) print(besselyzero(2,1)) print(besselyzero(2,2)) print(besselyzero(2,3))
Начальные нули производных от функций Бесселя
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1,1)) print(besselyzero(0,2,1)) print(besselyzero(0,3,1)) print(besselyzero(1,1,1)) print(besselyzero(1,2,1)) print(besselyzero(1,3,1)) print(besselyzero(2,1,1)) print(besselyzero(2,2,1)) print(besselyzero(2,3,1))
Нули с большим индексом:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,100)) print(besselyzero(0,1000)) print(besselyzero(0,10000)) print(besselyzero(5,100)) print(besselyzero(5,1000)) print(besselyzero(5,10000)) print(besselyzero(0,100,1)) print(besselyzero(0,1000,1)) print(besselyzero(0,10000,1))
Нули функций с большим порядком:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(50,1)) print(besselyzero(50,2)) print(besselyzero(50,100)) print(besselyzero(50,1,1)) print(besselyzero(50,2,1)) print(besselyzero(50,100,1))
Нули функций с дробным порядком:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0.5,1)) print(besselyzero(1.5,1)) print(besselyzero(2.25,4))
Приложения функций Бесселя
Важность функций Бесселя обусловлена не только частым появлением уравнения Бесселя в приложениях, но также и тем, что решения многих других линейных дифференциальных уравнений второго порядка могут быть выражены через функции Бесселя. Чтобы увидеть как они появляются, мы начнем с уравнения Бесселя порядка
и подставим сюда
Тогда, используя (2) и введя константы
Из уравнения (4) получим:
Если
где:
Продольный изгиб вертикальной колонны
Мы теперь рассмотрим задачу, важную для практических приложений. В этой задаче требуется определить, когда однородная вертикальная колонна согнется под ее собственным весом. Мы полагаем

Обозначим угловое отклонение колонны в точке
где
Будем решать задачу, используя (7) и (8) при:
Перепишем (7) с учётом (9) при условии (8):
Колонна может деформироваться, только если есть нетривиальное решение задачи (10); иначе колонна останется в не отклоненном от вертикали положении (т. е. физически не сможет отклониться от вертикали).
Дифференциальное уравнение (10) представляет собой уравнение Эйри. Уравнение (10) имеет форму уравнения (3) при
Поэтому общее решение имеет вид:
Чтобы применить начальные условия, мы подставляем
После преобразования (12), с учётом решения (11), получим:
При условии в начальной точке
При условии в конечной точке
Следует отметить, что преобразований (13), (14) можно было не делать, если построить графики функций
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) f1=lambda x: besselj(1/3,x) plot([f,f1], [0, 15])

Из графика следует, что при x=0 функция
Таким образом, колонна деформируется, только если
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) plot(f, [0, 15])

На графике видно, что первый корень немного меньше 2. Найти корень
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) print("z0=%s"%findroot(f, 1)
Получим:
Рассчитаем критическую длину, например флагштока, по формуле (15):
Высота флагштока для разных параметров в сечении
from numpy import* def LRr(R,r): E=2.9*10**11#н/м^2 rou=7900#кг/м^3 g=9.8#м/с^2 I=pi*((R-r)**4)/4#м^4 F=pi*(R-r)**2#м^2 return 1.086*(E*I/(rou*g*F))**1/3 R=5*10**-3 r=0 L= LRr(R,r) print(round(L,2),"м") R=7.5*10**-3 r=2*10**-3 Lr= LRr(R,r) print(round(Lr,2),"м")
Получим:
8.47 м
10.25 м
Полый флагшток может быть выше, чем сплошной.
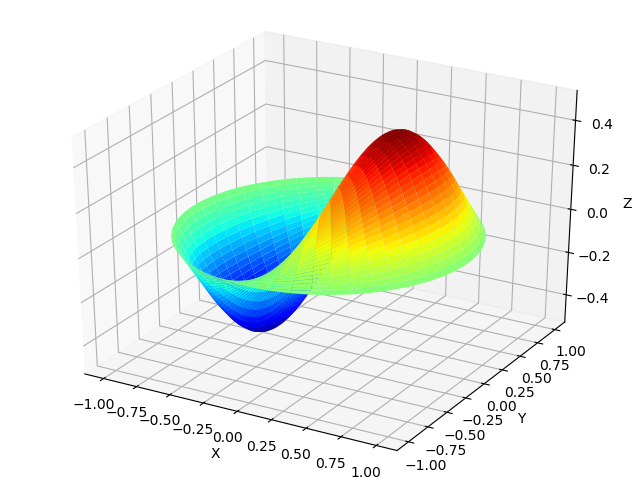
Распространение волн в тонкой мембране.
Тонкая мембрана при попадании на неё звуковых волн не только колеблется с частотой волн. Форму колебаний мембраны можно получить в функциях Бесселя по следующему листингу, пользуясь формулами besselj() и besseljzero():
Форма колебаний мембраны
from mpmath import* from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm def Membrana(r): mp.dps=25 return cos(0.5) * cos( theta) *float(besselj(1,r*besseljzero(1,1) ,0)) theta =linspace(0,2*pi,50) radius = linspace(0,1,50) x = array([r * cos(theta) for r in radius]) y = array([r * sin(theta) for r in radius]) z = array([Membrana(r) for r in radius]) fig = plt.figure("Мембрана") ax = Axes3D(fig) ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_zlabel('Z') plt.show()

Альтернатива модулю mpmath в специальных функциях Бесселя библиотеки SciPy
Не углубляясь в детальное рассмотрение функций Бесселя из библиотеки SciPy[4], приведу только два листинга для построения графиков функций первого и второго рода jv(v, x), yv(v, x):
jv(v, x)
import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.jv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$J_{0}(x)$', '$ J_{1}(x)$', '$J_{2}(x)$', '$J_{3}(x)$', '$ J_{4}(x)$','$ J_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('${J}_n(x)$') py.grid(True) py.show()

yv(v, x)
import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.yv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$Y_{0}(x)$', '$ Y_{1}(x)$', '$Y_{2}(x)$', '$Y_{3}(x)$', '$ Y_{4}(x)$','$ Y_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('$Y_{n}(x)$') py.grid(True) py.show()

Выводы:
В статье изложены основы работы с функциями Бесселя при помощи библиотек mpmath, sympy и scipy, приведены примеры применения функций для решения дифференциальных уравнений. Статья может быть полезна при изучении уравнений математической физики.
Ссылки:
1.Функции Бесселя
2.Использование обратного преобразования Лапласа для анализа динамических звеньев систем управления
3.Bessel function related functions
4. Special functions (scipy.special).
