В последнее время мы в группе распознавания компании ABBYY всё больше применяем нейронные сети в различных задачах. Очень хорошо они зарекомендовали себя в первую очередь для сложных видов письменности. В прошлых постах мы рассказывали о том, как мы используем нейронные сети для распознавания японской, китайской и корейской письменности.
Пост про распознавания японских и китайских иероглифов
Пост про распознавание корейских символов
В обоих случаях мы использовали нейронные сети с целью полной замены метода классификации отдельного символа. Во всех подходах фигурировало множество различных сетей, и в задачи некоторых из них входила необходимость адекватно работать на изображениях, которые не являются символами. Модель в этих ситуациях должна как-то сигнализировать о том, что перед нами не символ. Сегодня мы как раз расскажем о том, зачем это в принципе может быть нужно, и о подходах, с помощью которых можно добиться желаемого эффекта.
А в чём вообще проблема? Зачем нужно работать на изображениях, которые не являются отдельными символами? Казалось бы, можно разделить фрагмент строки на символы, классифицировать их все и собрать из этого результат, как, например, на картинке ниже.
Да, конкретно в данном случае так действительно можно сделать. Но, увы, реальный мир устроен куда более сложно, и на практике при распознавании приходится иметь дело с геометрическими искажениями, смазом, пятнами кофе и прочими трудностями.
В итоге зачастую приходится работать вот с такими фрагментами:
Думаю, всем очевидно, в чём здесь проблема. По такому изображению фрагмента не так просто однозначно разбить его на отдельные символы, чтобы все их по-отдельности распознать. Приходится выдвигать набор гипотез о том, где находятся границы между символами, а где — сами символы. Для этого мы используем так называемый граф линейного деления (ГЛД). На картинке выше этот граф изображён в нижней части: зелёные отрезки – это дуги построенного ГЛД, то есть гипотезы о том, где находятся отдельные символы.
Таким образом, часть изображений, для которых запускается модуль распознавания отдельного символа, по факту являются не отдельными символами, а ошибками сегментации. И этот самый модуль должен просигнализировать о том, что перед ним, скорее всего, не символ, вернув низкую уверенность для всех вариантов распознавания. А если этого не произойдёт, то в итоге может быть выбран неправильный вариант сегментации этого фрагмента по символам, что сильно увеличит число ошибок линейного деления.
Помимо ошибок сегментации, модель также должна быть устойчива к априорному мусору со страницы. Например, вот такие изображения тоже могут подаваться на распознавание отдельного символа:
Если просто классифицировать такие изображения на отдельные символы, то результаты классификации будут попадать в результаты распознавания. При этом на самом деле эти изображения являются просто артефактами алгоритма бинаризации, им ничего не должно соответствовать в итоговом результате. А значит для них тоже нужно уметь возвращать низкую уверенность при классификации.
Все подобные изображения: ошибки сегментации, априорный мусор и т.д. мы в дальнейшем будем называть отрицательными примерами. Изображения же реальных символов будем называть положительными примерами.
Теперь вспомним, как работает обычная нейронная сеть для распознавания отдельных символов. Обычно это какой-то набор свёрточных и полносвязных слоёв, с помощью которого из входного изображения формируется вектор вероятностей принадлежности каждому конкретному классу.
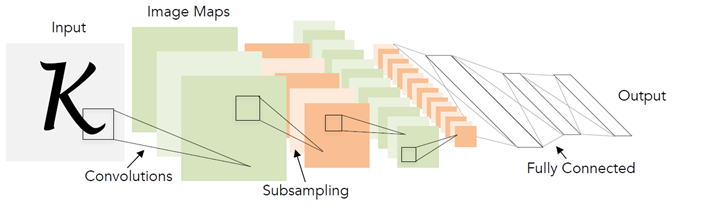
При этом число классов совпадает с размером алфавита. Во время обучения нейронной сети подают изображения реальных символов и учат её возвращать высокую вероятность для правильного класса символа.
А что будет происходить, если подавать нейронной сети на вход ошибки сегментации и априорный мусор? На самом деле, чисто теоретически может происходить всё что угодно, потому что подобные изображения сеть вовсе не видела в процессе обучения. Для каких-то изображений может повезти, и сеть вернёт низкую вероятность для всех классов. Но в некоторых случаях сеть может начать искать среди мусора на входе знакомые очертания некоторого символа, например, символа «А» и распознать его с вероятностью 0.99.
На практике, когда мы работали, например, над нейросетевой моделью для японской и китайской письменности, использование сырой вероятности с выхода сети приводило к появлению огромного числа ошибок сегментации. И, несмотря на то что символьная модель работала очень хорошо на базе изображений, встроить её в полный алгоритм распознавания не представлялось возможным.
У кого-то может возникнуть вопрос: почему именно с нейронными сетями возникает подобная проблема? Почему признаковые классификаторы не работали так же, ведь они тоже учились на базах изображений, а значит отрицательных примеров не было в процессе обучения?
Принципиальная разница, на мой взгляд, здесь в том, как именно выделяются признаки с изображений символов. В случае обычного классификатора, человек сам прописывает, каким образом их извлекать, руководствуясь какими-то своими знаниями об их устройстве. В случае нейронной сети, выделение признаков также является обучаемой частью модели: они настраиваются так, чтобы наилучшим образом можно было различать символы из разных классов. И на практике получается, что описанные человеком признаки являются более устойчивыми к изображениям, которые не являются символами: они с меньшей вероятностью будут такими же, как у изображений реальных символов, а значит для них можно вернуть меньшее значение уверенности.
Т.к. проблема по нашим подозрениям была в том, как нейронная сеть выделяет признаки, мы решили попробовать улучшить именно эту часть, то есть научиться выделять некоторые «хорошие» признаки. В глубоком обучении есть отдельный раздел, посвящённый этой теме, и называется он «Обучение представлений» (Representation Learning). Мы решили попробовать различные успешные подходы в этой области. Большая часть решений при этом предлагалась для обучения представлений в задачах распознавания лиц.
Неплохим показался подход, описанный в статье «A Discriminative Feature Learning Approach for Deep Face Recognition». Основная идея авторов: добавить в функцию потерь дополнительное слагаемое, которое будет уменьшать евклидово расстояние в признаковом пространстве между элементами одного класса.
При различных значениях веса этого слагаемого в общей функции потерь можно получать различные изображения в пространствах признаков:
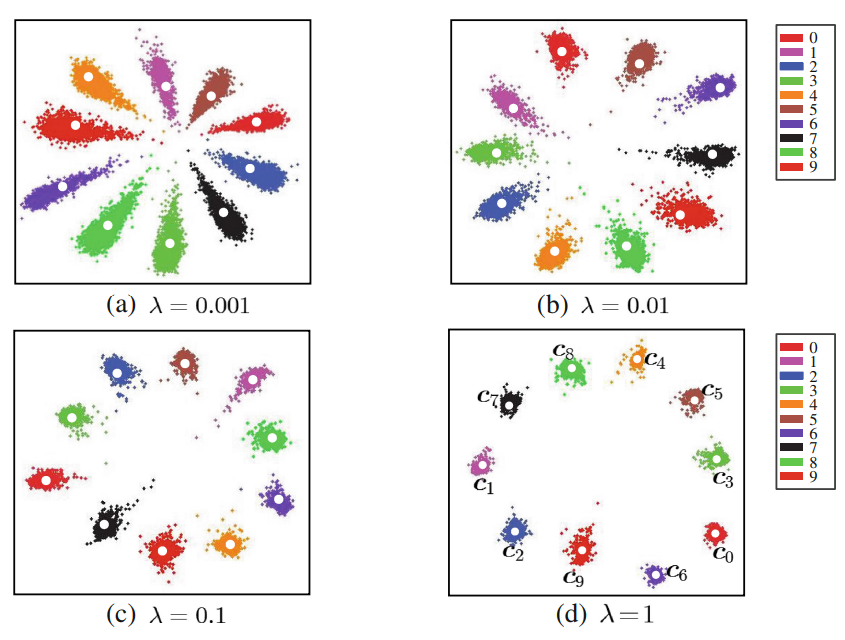
На этом рисунке представлено распределение элементов тестовой выборки в двумерном признаковом пространстве. Рассматривается задача классификации рукописных цифр (выборка MNIST).
Одно из важных свойств, которое было заявлено авторами: увеличение обобщающей способности получаемых признаков для лиц, которых не было в обучающей выборке. Лица одних людей всё так же располагались рядом, а лица разных людей – далеко друг от друга.
Мы решили проверить, сохраняется ли похожее свойство для выборки символов. При этом руководствовались следующей логикой: если в признаковом пространстве все элементы одного класса сгруппированы компактно возле одной точки, то признаки для отрицательных примеров будут с меньшей вероятностью располагаться возле этой же точки. Поэтому в качестве основного критерия для фильтрации мы использовали евклидово расстояние до статистического центра конкретного класса.
Для проверки гипотезы мы поставили следующий эксперимент: обучили модели для распознавания небольшого подмножества японских символов из слоговых азбук (так называемой каны). Помимо обучающей выборки мы рассмотрели также 3 искусственных базы отрицательных примеров:
Нам хотелось сравнить классический подход с функцией потерь Cross Entropy и подход с Center Loss по способности фильтровать отрицательные примеры. Критерии фильтрации отрицательных примеров были разными. В случае Cross Entropy Loss мы использовали отклик сети с последнего слоя, а в случае Center Loss – евклидово расстояние до статистического центра класса в признаковом пространстве. В обоих случаях мы выбрали порог соответствующей статистики, при котором отсеивается не более 3% положительных примеров из тестовой выборки и посмотрели на долю отрицательных примеров из каждой базы, которая отсеивается по данному порогу.
Как можно видеть Center Loss подход действительно лучше справляется с фильтрацией отрицательных примеров. При этом в обоих случаях у нас не было изображений отрицательных примеров в процессе обучения. Это на самом деле очень неплохо, потому что в общем случае получить репрезентативную базу всех отрицательных примеров в задаче OCR – не самая простая задача.
Мы применили этот подход для задачи распознавания японских символов (на втором уровне двухуровневой модели), и результат нас порадовал: число ошибок линейного деления сократилось в разы. Хоть ошибки и оставались, их можно было уже классифицировать по конкретным типам: будь то пары цифр или иероглифы с приклеившимся символом пунктуации. Для этих ошибок уже можно было сформировать некоторую синтетическую базу отрицательных примеров и использовать её в процессе обучения. О том, какими способами это можно делать, и пойдёт речь дальше.
Если у вас есть некоторая коллекция отрицательных примеров, то глупо её не использовать в процессе обучения. Но давайте подумаем, как это можно сделать.
Для начала рассмотрим наиболее простую схему: все отрицательные примеры группируем в отдельный класс и добавляем ещё один нейрон в выходной слой, соответствующий этому классу. Теперь на выходе у нас распределение вероятностей на N + 1 класс. И учим мы это обычным Cross-Entropy Loss.
Критерием того, что пример является отрицательным, можно считать величину соответствующего нового отклика сети. Но иногда реальные символы не очень высокого качества могут быть классифицированы как отрицательные примеры. Можно ли сделать переход между положительными и отрицательными примерами более плавным?
На самом деле, можно попробовать не увеличивать общее число выходов, а просто заставить модель при обучении возвращать низкие отклики для всех классов при подаче на вход отрицательных примеров. Для этого мы можем не добавлять явно в модель N+1-ый выход, а просто добавить N+1-ым элементом значение –max от откликов для всех остальных классов. Тогда, при подаче отрицательных примеров на вход, это значение сеть будет пытаться сделать как можно больше, а значит величину максимального отклика будет пытаться сделать как можно меньше.
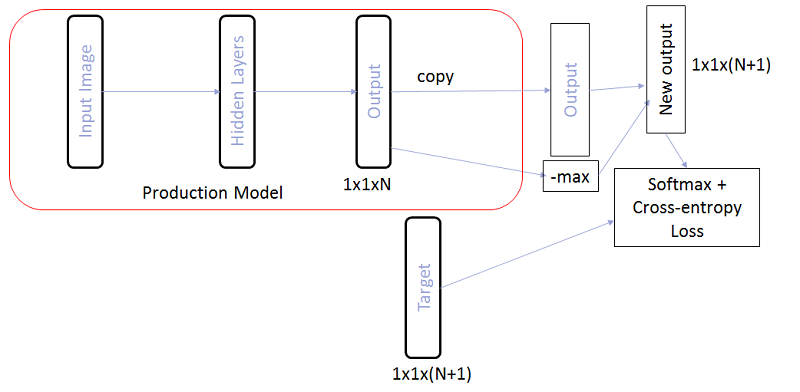
Ровно такую схему мы применили на первом уровне двухуровневой модели для японского в комбинации с Center Loss подходом на втором уровне. Таким образом, часть отрицательных примеров фильтровалась на первом уровне, а часть – на втором. В комбинации уже удалось получить решение, готовое к встраиванию в общий алгоритм распознавания.
В целом можно также задаться вопросом: как использовать базу отрицательных примеров в подходе с Center Loss? Получается, что нам как-то нужно отдалить отрицательные примеры, которые расположены близко к статистическим центрам классов в признаковом пространстве. Как же заложить эту логику в функцию потерь?
Пусть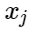
— признаки отрицательных примеров, а 
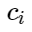— центры классов. Тогда можно рассмотреть следующую добавку для функции потерь:
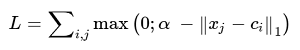
Здесь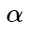
– некоторый допустимый зазор между центром и отрицательными примерами, внутри которого на отрицательные примеры накладывается штраф.
Комбинацию Center Loss с добавкой, описанной выше, мы успешно применили, например, для некоторых отдельных классификаторов в задаче распознавания корейских символов.
В целом, все описанные выше подходы к фильтрации так называемых «отрицательных примеров» можно применять в любых задачах классификации, когда у вас имеется некоторый неявный сильно несбалансированный относительно остальных класс без хорошей базы представителей, с которым, тем не менее, нужно как-то считаться. OCR – лишь некоторая частная задача, в которой эта проблема стоит наиболее остро.
Естественно, все эти проблемы возникают только при использовании нейронных сетей в качестве основной модели для распознавания отдельных символов. При использовании же End-to-End распознавания строк целиком отдельной моделью подобной проблемы не возникает.
OCR New Technologies Group
Пост про распознавания японских и китайских иероглифов Пост про распознавание корейских символовВ обоих случаях мы использовали нейронные сети с целью полной замены метода классификации отдельного символа. Во всех подходах фигурировало множество различных сетей, и в задачи некоторых из них входила необходимость адекватно работать на изображениях, которые не являются символами. Модель в этих ситуациях должна как-то сигнализировать о том, что перед нами не символ. Сегодня мы как раз расскажем о том, зачем это в принципе может быть нужно, и о подходах, с помощью которых можно добиться желаемого эффекта.
Мотивация
А в чём вообще проблема? Зачем нужно работать на изображениях, которые не являются отдельными символами? Казалось бы, можно разделить фрагмент строки на символы, классифицировать их все и собрать из этого результат, как, например, на картинке ниже.
Да, конкретно в данном случае так действительно можно сделать. Но, увы, реальный мир устроен куда более сложно, и на практике при распознавании приходится иметь дело с геометрическими искажениями, смазом, пятнами кофе и прочими трудностями.
В итоге зачастую приходится работать вот с такими фрагментами:
Думаю, всем очевидно, в чём здесь проблема. По такому изображению фрагмента не так просто однозначно разбить его на отдельные символы, чтобы все их по-отдельности распознать. Приходится выдвигать набор гипотез о том, где находятся границы между символами, а где — сами символы. Для этого мы используем так называемый граф линейного деления (ГЛД). На картинке выше этот граф изображён в нижней части: зелёные отрезки – это дуги построенного ГЛД, то есть гипотезы о том, где находятся отдельные символы.
Таким образом, часть изображений, для которых запускается модуль распознавания отдельного символа, по факту являются не отдельными символами, а ошибками сегментации. И этот самый модуль должен просигнализировать о том, что перед ним, скорее всего, не символ, вернув низкую уверенность для всех вариантов распознавания. А если этого не произойдёт, то в итоге может быть выбран неправильный вариант сегментации этого фрагмента по символам, что сильно увеличит число ошибок линейного деления.
Помимо ошибок сегментации, модель также должна быть устойчива к априорному мусору со страницы. Например, вот такие изображения тоже могут подаваться на распознавание отдельного символа:
Если просто классифицировать такие изображения на отдельные символы, то результаты классификации будут попадать в результаты распознавания. При этом на самом деле эти изображения являются просто артефактами алгоритма бинаризации, им ничего не должно соответствовать в итоговом результате. А значит для них тоже нужно уметь возвращать низкую уверенность при классификации.
Все подобные изображения: ошибки сегментации, априорный мусор и т.д. мы в дальнейшем будем называть отрицательными примерами. Изображения же реальных символов будем называть положительными примерами.
Проблема нейросетевого подхода
Теперь вспомним, как работает обычная нейронная сеть для распознавания отдельных символов. Обычно это какой-то набор свёрточных и полносвязных слоёв, с помощью которого из входного изображения формируется вектор вероятностей принадлежности каждому конкретному классу.
При этом число классов совпадает с размером алфавита. Во время обучения нейронной сети подают изображения реальных символов и учат её возвращать высокую вероятность для правильного класса символа.
А что будет происходить, если подавать нейронной сети на вход ошибки сегментации и априорный мусор? На самом деле, чисто теоретически может происходить всё что угодно, потому что подобные изображения сеть вовсе не видела в процессе обучения. Для каких-то изображений может повезти, и сеть вернёт низкую вероятность для всех классов. Но в некоторых случаях сеть может начать искать среди мусора на входе знакомые очертания некоторого символа, например, символа «А» и распознать его с вероятностью 0.99.
На практике, когда мы работали, например, над нейросетевой моделью для японской и китайской письменности, использование сырой вероятности с выхода сети приводило к появлению огромного числа ошибок сегментации. И, несмотря на то что символьная модель работала очень хорошо на базе изображений, встроить её в полный алгоритм распознавания не представлялось возможным.
У кого-то может возникнуть вопрос: почему именно с нейронными сетями возникает подобная проблема? Почему признаковые классификаторы не работали так же, ведь они тоже учились на базах изображений, а значит отрицательных примеров не было в процессе обучения?
Принципиальная разница, на мой взгляд, здесь в том, как именно выделяются признаки с изображений символов. В случае обычного классификатора, человек сам прописывает, каким образом их извлекать, руководствуясь какими-то своими знаниями об их устройстве. В случае нейронной сети, выделение признаков также является обучаемой частью модели: они настраиваются так, чтобы наилучшим образом можно было различать символы из разных классов. И на практике получается, что описанные человеком признаки являются более устойчивыми к изображениям, которые не являются символами: они с меньшей вероятностью будут такими же, как у изображений реальных символов, а значит для них можно вернуть меньшее значение уверенности.
Повышение устойчивости модели с помощью Center Loss
Т.к. проблема по нашим подозрениям была в том, как нейронная сеть выделяет признаки, мы решили попробовать улучшить именно эту часть, то есть научиться выделять некоторые «хорошие» признаки. В глубоком обучении есть отдельный раздел, посвящённый этой теме, и называется он «Обучение представлений» (Representation Learning). Мы решили попробовать различные успешные подходы в этой области. Большая часть решений при этом предлагалась для обучения представлений в задачах распознавания лиц.
Неплохим показался подход, описанный в статье «A Discriminative Feature Learning Approach for Deep Face Recognition». Основная идея авторов: добавить в функцию потерь дополнительное слагаемое, которое будет уменьшать евклидово расстояние в признаковом пространстве между элементами одного класса.
При различных значениях веса этого слагаемого в общей функции потерь можно получать различные изображения в пространствах признаков:
На этом рисунке представлено распределение элементов тестовой выборки в двумерном признаковом пространстве. Рассматривается задача классификации рукописных цифр (выборка MNIST).
Одно из важных свойств, которое было заявлено авторами: увеличение обобщающей способности получаемых признаков для лиц, которых не было в обучающей выборке. Лица одних людей всё так же располагались рядом, а лица разных людей – далеко друг от друга.
Мы решили проверить, сохраняется ли похожее свойство для выборки символов. При этом руководствовались следующей логикой: если в признаковом пространстве все элементы одного класса сгруппированы компактно возле одной точки, то признаки для отрицательных примеров будут с меньшей вероятностью располагаться возле этой же точки. Поэтому в качестве основного критерия для фильтрации мы использовали евклидово расстояние до статистического центра конкретного класса.
Для проверки гипотезы мы поставили следующий эксперимент: обучили модели для распознавания небольшого подмножества японских символов из слоговых азбук (так называемой каны). Помимо обучающей выборки мы рассмотрели также 3 искусственных базы отрицательных примеров:
- Pairs – набор пар европейских символов
- Cuts – фрагменты японских строк, вырезанными по просветам, не являющиеся символами
- Not kana – другие символы из японского алфавита, не относящиеся к рассмотренному подмножеству
Нам хотелось сравнить классический подход с функцией потерь Cross Entropy и подход с Center Loss по способности фильтровать отрицательные примеры. Критерии фильтрации отрицательных примеров были разными. В случае Cross Entropy Loss мы использовали отклик сети с последнего слоя, а в случае Center Loss – евклидово расстояние до статистического центра класса в признаковом пространстве. В обоих случаях мы выбрали порог соответствующей статистики, при котором отсеивается не более 3% положительных примеров из тестовой выборки и посмотрели на долю отрицательных примеров из каждой базы, которая отсеивается по данному порогу.
Как можно видеть Center Loss подход действительно лучше справляется с фильтрацией отрицательных примеров. При этом в обоих случаях у нас не было изображений отрицательных примеров в процессе обучения. Это на самом деле очень неплохо, потому что в общем случае получить репрезентативную базу всех отрицательных примеров в задаче OCR – не самая простая задача.
Мы применили этот подход для задачи распознавания японских символов (на втором уровне двухуровневой модели), и результат нас порадовал: число ошибок линейного деления сократилось в разы. Хоть ошибки и оставались, их можно было уже классифицировать по конкретным типам: будь то пары цифр или иероглифы с приклеившимся символом пунктуации. Для этих ошибок уже можно было сформировать некоторую синтетическую базу отрицательных примеров и использовать её в процессе обучения. О том, какими способами это можно делать, и пойдёт речь дальше.
Использование базы отрицательных примеров при обучении
Если у вас есть некоторая коллекция отрицательных примеров, то глупо её не использовать в процессе обучения. Но давайте подумаем, как это можно сделать.
Для начала рассмотрим наиболее простую схему: все отрицательные примеры группируем в отдельный класс и добавляем ещё один нейрон в выходной слой, соответствующий этому классу. Теперь на выходе у нас распределение вероятностей на N + 1 класс. И учим мы это обычным Cross-Entropy Loss.
Критерием того, что пример является отрицательным, можно считать величину соответствующего нового отклика сети. Но иногда реальные символы не очень высокого качества могут быть классифицированы как отрицательные примеры. Можно ли сделать переход между положительными и отрицательными примерами более плавным?
На самом деле, можно попробовать не увеличивать общее число выходов, а просто заставить модель при обучении возвращать низкие отклики для всех классов при подаче на вход отрицательных примеров. Для этого мы можем не добавлять явно в модель N+1-ый выход, а просто добавить N+1-ым элементом значение –max от откликов для всех остальных классов. Тогда, при подаче отрицательных примеров на вход, это значение сеть будет пытаться сделать как можно больше, а значит величину максимального отклика будет пытаться сделать как можно меньше.
Ровно такую схему мы применили на первом уровне двухуровневой модели для японского в комбинации с Center Loss подходом на втором уровне. Таким образом, часть отрицательных примеров фильтровалась на первом уровне, а часть – на втором. В комбинации уже удалось получить решение, готовое к встраиванию в общий алгоритм распознавания.
В целом можно также задаться вопросом: как использовать базу отрицательных примеров в подходе с Center Loss? Получается, что нам как-то нужно отдалить отрицательные примеры, которые расположены близко к статистическим центрам классов в признаковом пространстве. Как же заложить эту логику в функцию потерь?
Пусть
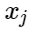— признаки отрицательных примеров, а 
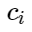— центры классов. Тогда можно рассмотреть следующую добавку для функции потерь: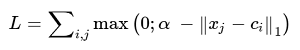 
Здесь
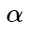– некоторый допустимый зазор между центром и отрицательными примерами, внутри которого на отрицательные примеры накладывается штраф. Комбинацию Center Loss с добавкой, описанной выше, мы успешно применили, например, для некоторых отдельных классификаторов в задаче распознавания корейских символов.
Выводы
В целом, все описанные выше подходы к фильтрации так называемых «отрицательных примеров» можно применять в любых задачах классификации, когда у вас имеется некоторый неявный сильно несбалансированный относительно остальных класс без хорошей базы представителей, с которым, тем не менее, нужно как-то считаться. OCR – лишь некоторая частная задача, в которой эта проблема стоит наиболее остро.
Естественно, все эти проблемы возникают только при использовании нейронных сетей в качестве основной модели для распознавания отдельных символов. При использовании же End-to-End распознавания строк целиком отдельной моделью подобной проблемы не возникает.
OCR New Technologies Group
