

В первой части этого поста я рассказал, как многократное применение стандартных halfpel-фильтров создаёт искажённые изображения, а затем показал новый фильтр, не имеющий данной проблемы.
Он был немного более размытым и это устроит не всех. Однако он был лучше своих альтернатив — на самом деле именно этот фильтр использовался в оригинальной версии Bink 2. Из-за постоянной нагрузки на работе мне никогда не удавалось вернуться к нему снова и исследовать его подробнее.
Но теперь, когда я нашёл время для возврата к этому фильтру и написания статьи о нём, мне наконец стоит задаться вопросом: существует ли менее размывающий фильтр, который всё же сохраняет свойство «бесконечной стабильности»?
Предупреждение о спойлерах: правильный ответ — «вероятно, нет» и «определённо, есть». Но прежде чем мы дойдём до того, почему на этот вопрос есть два ответа и что они означают, давайте получше подготовим испытательный стенд.
Корректировка для сдвига
Когда я изначально работал над этой проблемой, то понятия не имел, что ищу. Я даже не знал что существует такая штука, как «бесконечно стабильный» halfpel-фильтр, поэтому не создавал систему в его поисках. Я просто искал что-нибудь, что выдержит «множество» итераций фильтра без искажений изображения. Все изображения из первой части отражают эту методологию: изображение сдвигается справа налево по полпикселя за раз, то есть если применить фильтр 100 раз, получившееся изображение будет смещено на 50 пикселей.
Теперь, когда мы знаем, что ищем на самом деле, можно быть немного точнее. Применив halfpel-фильтр два раза, мы смещаем изображение ровно на один пиксель. То есть если мы просто переместим изображение на один пиксель назад, то оно останется в том же пространстве. Благодаря этому тест будет выглядеть намного красивее, потому то мы не только сможем применять фильтр любое количество раз, не боясь, что изображение «уползёт» с экрана, но и сможем найти разность изображения с предыдущими версиями и с оригиналом.
Это позволит нам тестировать фильтры автоматически. Мы просто многократно применим фильтр и увидим одно из двух: или сходимость к неизменяемому изображению, обозначающему, что фильтр бесконечно стабилен, или значительно большое отклонение от оригинального изображения, показывающее, что фильтр «сломался». Для этих тестов я выбрал в качестве «значительно большой» среднюю погрешность на канал 64 (из 255), или максимальную погрешность на любой из каналов в полные 255. Если какое-то из этих условий выполнится, то мы будем считать, что фильтр «сломался».
Повторное тестирование фильтров из первой части
Так, теперь мы лучше понимаем, как тестировать эти фильтры, поэтому давайте взглянем по-новому на фильтры из первой части. Начнём с билинейного, который, разумеется, не очень интересен:

Это картина после 244 итераций. Как и можно ожидать, изображение постепенно «ломается» из-за постоянного усреднения пикселей. Но даже оно постепенно достигает предела средней погрешности.
Вот h.264:
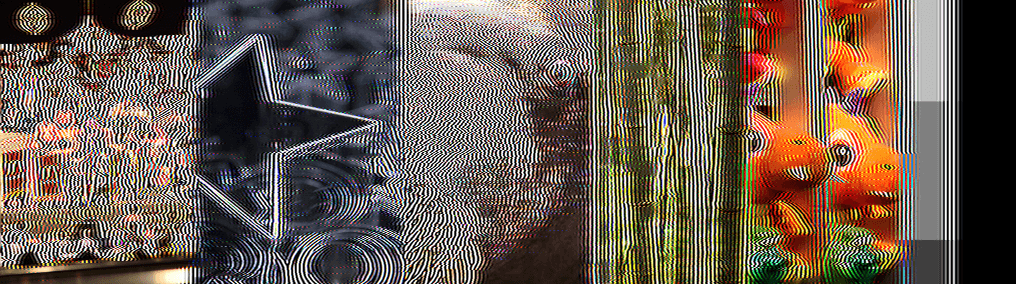
Чтобы сломать изображение, ему хватает 78 итераций. Фильтр HEVC с 8 сэмплами ведёт себя немного лучше, но всё равно ломается через 150 итераций:

Lanczos с 6 сэмплами ломается через 166 итераций:

Вот и все наши сломавшиеся фильтры. Остался только мой целочисленный фильтр:

Как и ожидалось, он единственный не сломался. Он сходится к бесконечно стабильному изображению через 208 итераций.
Здесь довольно примечательно то, что мы знаем: по крайней мере, для широкого набора тестовых изображений этот фильтр бесконечно стабилен, то есть он никогда не создаст артефакт, сколько бы раз его ни применяли.
Это возвращает нас к первоначальному вопросу: на самом ли деле он наилучший? И вы уже знаете ответы, потому что я проспойлерил и в начале статьи: «вероятно, нет» и «определённо, да».
Давайте сначала рассмотрим сначала часть с «вероятно, нет».
Целочисленные фильтры
Итак, в первой части поста я упоминал, что найденное мной ядро фильтра «лучшим из обнаруженных», и в этом его особенность. И вот в чём заключается особенность:
Когда я искал этот фильтр, на самом деле я не искал лучший фильтр. Я искал наилучший фильтр, который можно выразить очень небольшим числом целочисленных сдвигов, сложений и вычитаний. Это может показаться странным, но не торопитесь.
Возможно, вы заметили, что когда я показывал коэффициенты h.264, HEVC и билинейного фильтра, а также моего фильтра, я записывал их как целочисленные числители над целочисленными знаменателями, вот так:
MyKernel[] = {1.0/32.0, -4.0/32.0, 19.0/32.0, 19.0/32.0, -4.0/32.0, 1.0/32.0};Но в случае windowed sinc я поступил иначе и записал его вот так:
LanczosKernel[] = {0.02446, -0.13587, 0.61141, 0.61141, -0.13587, 0.02446};Причина этого заключается в том, что windowed sinc на самом деле выведен из непрерывной математической функции, не имеющей ничего общего с обычными целочисленными дробями. При использовании этого фильтра используются числа с плавающей запятой (как можно точнее) соответствующие значениям функции sinc. Если стремиться применить их точно, то не стоит округлять их до обычных дробей, потому что это добавит погрешность.
Видеокодеки традиционно не могут себе позволить выполнять такие операции. Операции с плавающей запятой над такими «тяжёлыми» задачами, как компенсация движения, просто невозможно использовать на маломощном или специализированном оборудовании. Это особенно справедливо, если мы говорим об кодеках отраслевых стандартов, которые должны работать на широком диапазоне устройств, в том числе на дешёвых встраиваемых чипах с низким энергопотреблением.
Более того, даже если выполнять их на ЦП, современные наборы инструкций основаны на SIMD, то есть целочисленные операции в ЦП всё равно могут выполняться быстрее: можно уместить два 16-битных integer в пространство одного 32-битного float, по сути удвоив производительность операций, поэтому если рассматривать точное количество циклов на операции, то плавающая запятая не всегда является самым быстрым вариантом.
Теперь вы видите, почему эта особенность была важна. Так как мне нужны были только простые 16-битные целочисленные операции, я искал те ядра, которые можно выразить как небольшие целые числа над делителями в степени двойки до 64 и не более. Это гораздо более ограниченное множество фильтров по сравнению с тем, если бы я рассматривал любое множество из 6 коэффициентов с плавающей запятой.
Аналогично, из соображений эффективности я не рассматривал никакое другое количество сэмплов. Единственным вариантом было 6 или меньше, поэтому я даже не тестировал версии с 8 или 10 сэмплами.
Таким образом мы пришли к первому ответу: «вероятно, нет». Если мы будем придерживаться этих ограничений, то скорее всего не найдём более хорошего фильтра, который можно применить бесконечное количество раз без деградации. Ядро фильтра из первой части — это, вероятно, лучшее, что мы можем найти, хотя и надо признать, что я не могу доказать этого исчерпывающе.
Но что если нам не нужно придерживаться таких ограничений?
Версия с плавающей запятой
Если мы избавимся от ограничений, специфичных для исходной версии Bink 2 (которая теперь довольно устарела — с тех пор вышло много ревизий), и воспользуемся произвольными коэффициентами с плавающей запятой, то насколько можно улучшить результаты?
Ну, поскольку мы знаем, что моё целочисленное ядро никогда не деградирует, и мы знаем, что у Lanczos выше резкость, но он деградирует, то логично, что мы сможем найти место между двумя множествами коэффициентов, где начинается деградация. Поэтому я написал программу, которая помогла мне найти эту конкретную точку, и вот какое ядро я обнаружил:
MyFloatKernel6[] = {0.027617, -0.130815, 0.603198, 0.603198, -0.130815, 0.027617};Для схождения этому ядру требуется 272 итераций, но оно бесконечно стабильно и выглядит намного резче, чем мой целочисленный фильтр:

На самом деле он почти неотличим от оригинала:

Почти… но не совсем. Если приглядеться, то в высококонтрастных областях всё равно можно заметить размытие и затухание. Проще всего это увидеть в глазу оранжевого «динозавра» и на ярких светлых участках за бамбуком.
То есть 6-сэмпловый фильтр с плавающей запятой определённо лучше, но он не идеален. Можно ли ещё его улучшить?
Увеличение ширины фильтра
Изначально фильтр с 6 сэмплами выбирался по тем же причинам, что и дроби с малыми целыми числами: я искал чрезвычайно эффективный фильтр. Но сейчас мы проводим исследования и уже перешли к числам с плавающей запятой, так почему бы не рассмотреть и более широкий фильтр?
Соединив наш 6-сэмпловый целочисленный фильтр с 6-сэмповым Lanczos, мы получили очень хороший фильтр. Почему бы нам не соединить его с 8-сэмпловым Lanczos?
8-сэмпловый Lanczos выглядит так:
Lanczos8[] = {-0.01263, 0.05976, -0.16601, 0.61888, 0.61888, -0.16601, 0.05976, -0.01263};Как и 6-сэмпловый Lanczos, он очень нестабилен и разрушается после 178 итераций:

Если мы поищем фильтр получше между 6-сэмпловым целочисленным фильтром и 8-сэмпловым Lanczos, то найдём этот довольно примечательный 8-сэмпловый фильтр:
MyFloatKernel8[] = {-0.010547, 0.052344, -0.156641, 0.614844, 0.614844, -0.156641, 0.052344, -0.010547};Как бесконечно стабильный фильтр он проявляет себя потрясающе хорошо. Он сходится через 202 итерации (сходимость быстрее, чем у двух моих фильтров), и так сильно походит на оригинал, что сложно разобрать, где из них что:

Вот ещё раз оригинал для справки:

По сравнению с моим исходным целочисленным фильтром налицо значительное улучшение.
Как работают бесконечно стабильные фильтры?
Я собирался завершить этот пост примерно так:
«Я не знаю точно, как всё это работает. В других областях, где я работал с бесконечно применяемыми преобразованиями, я знаю, как выполняется математика границ и создаётся полезный анализ. Прежде всего в голову приходит анализ граничной поверхности для поверхностей подразбиения, где вычисляются собственные значения и собственные векторы матрицы подразбиения, после чего можно точно взять предел в бесконечной степени. Но у меня нет опыта выполнения подобного анализа для halfpel-фильтров, потому что они не оставляют пиксели на месте, а сдвигают их вбок».
Таким был мой план. Но между написанием первой и второй частей я отправил по почте результаты улучшенного фильтра Фабьену Гисену и Чарльзу Блуму. Неудивительно, что они знали математику, необходимую для аналитического изучения этой задачи. Оказалось, что для фильтров и в самом деле существует анализ собственных значений и векторов, только выполняется он не совсем так.
Но его можно запросто выполнить — на самом деле он встроен в программы CAM как тривиальный одноэтапный процесс и мы действительно можем посмотреть на собственные значения для фильтров. Он не даёт нам полных ответов, потому что здесь важен факт округления (или усечения) до 8 бит (или 10 бит, или 12 бит) после каждого наложения фильтра, потому что усечение влияет на способ накопления погрешностей по сравнению с бесконечно точной алгеброй.
К сожалению, поскольку это совершенно не моя область знаний, я даже близко не могу сделать обзор этого анализа. Я спросил Фабьена и Чарльза, смогут ли они написать посты с той хорошей информацией, которую отправили мне по почте (у них обоих есть технические блоги — the ryg blog и cbloom rants), и Фабьен написал превосходную серию статей о математических основах стабильных фильтров. Если вам интересно теоретическое устройство того, что происходит в двух моих постах, то рекомендую прочитать эту серию!






