ashagraev 5 мая 2020 в 10:45

Леммы о разрастании для регулярных и контекстно-свободных языков

12 мин

12K

Две леммы о разрастании — утверждения, использующиеся для доказательства ограниченности важных классов формальных языков: регулярных и контекстно-свободных. Важность этих классов для программистов понять легко: регулярные выражения (один из видов описания регулярных языков) в работе используются достаточно часто, а уж языки программирования, синтаксис которых описывается контекстно-свободными грамматиками, и подавно.

Леммы очень похожи одна на другую как формулировками, так и доказательствами. Эта близость показалась мне настолько замечательной, что я решил посвятить этому целую статью.

План такой: разбираемся, что такое регулярные языки и какова связь между регулярными выражениями и конечными автоматами, формулируем и доказываем лемму о разрастании для регулярных языков, используем её для доказательства нерегулярности нескольких языков. Затем похожий трюк проделываем с контекстно-свободными языками, по пути выясняя, как они связаны с регулярными языками и как обходить обнаруженные ограничения при помощи грамматик общего вида. Поехали!

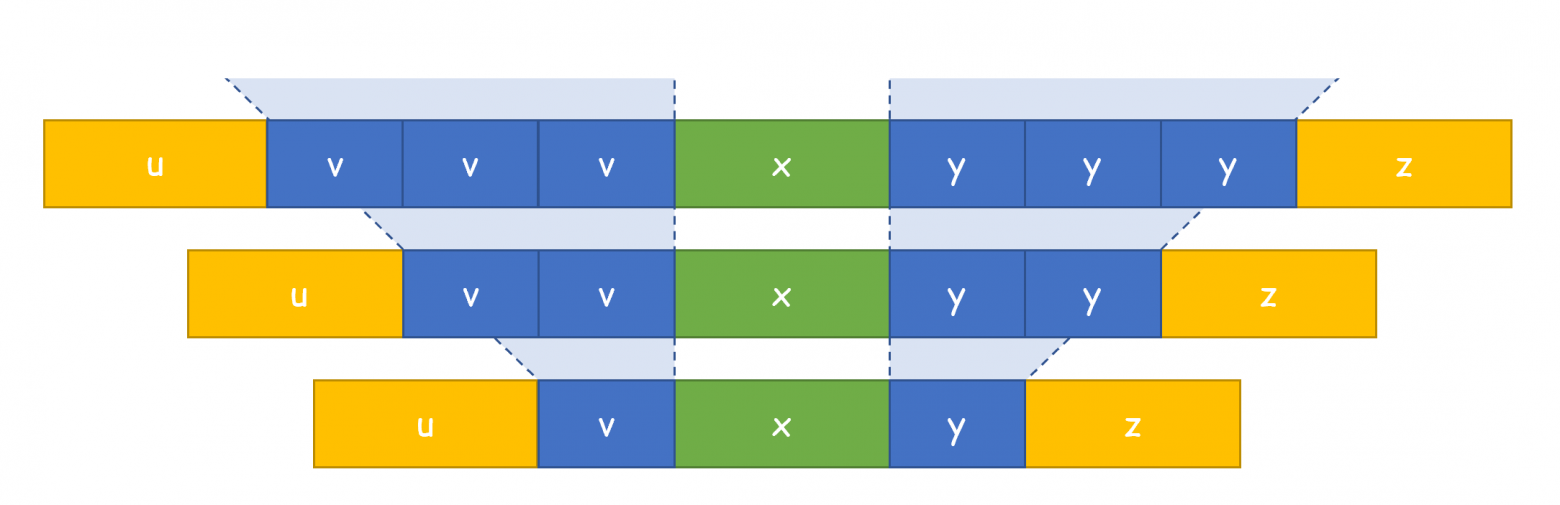
КДПВ иллюстрирует процесс разрастания для КС-грамматик

Формальный язык — произвольное множество строк (то есть, просто последовательностей) в конечном алфавите символов. Строки, составляющие язык, также называют словами. Алфавит обычно обозначают большой сигмой: $\Sigma$ . Специальным образом выделяется пустое слово, т.е. слово нулевой длины, не содержащее ни одного символа: $\varepsilon$ .

Если язык конечный (т.е. содержит некоторое конкретное число различных слов), описать его просто: можно предъявить все входящие в него слова. Поэтому интересно обсуждать описания потецинально бесконечных языков. Таких способов придумано очень много, но сегодня мы обсудим два вполне конкретных.

1. Регулярные языки и регулярные выражения

Регулярные языки строятся индуктивно: вначале описываются языки самого простого вида, а затем правила, при помощи которых из более простых языков можно получать более сложные.

Простейшие языки, относящиеся к классу регулярных:

$\varnothing$ — язык, не содержащий ни одного слова;
$\{\varepsilon\}$ — язык, содержащий только одно, пустое, слово;
$\{a\}, a \in \Sigma$ — язык, содержащий одно однобуквенное слово.

Теперь можно ввести операции над регулярными языками. Если $inline$ и $inline$ — регулярные языки, регулярными языками также будут следующие:

$A \cup B$ — объединение;
$A \cdot B = \{\alpha \beta | \alpha \in A, \beta \in B \}$ — конкатенация: множество строк, для которых префикс является словом из множества $inline$ , а суффикс является словом из множества $inline$ ;
$A^*= \{\alpha_1 \alpha_2 ... \alpha_k | k \in \mathbb{N}_0, \alpha_i \in A \}$ — итерация: $inline$ раз записанные друг за другом слова из $inline$ , причём $inline$ является произвольным натуральным числом или нулём.

Замечание: я использую обозначение $\mathbb{N}_0 = \mathbb{N} \cup \{0\}$ , чтобы избежать полемики по вопросу о том, является ли ноль натуральным числом

Для простоты записи знак конкатенации часто опускают: $A \cdot B = AB$ .

В программистской реальности регулярные языки возникают при работе с регулярными выражениями. Например, очень востребованным является регулярное выражения для определения строчек, являющихся ссылками. В своё время меня очень впечатлило выражение, используемое в программе PuTTY, а сейчас при помощи любого поисковика можно найти что-нибудь такое:

http[s]?://(?:[a-zA-Z]|[0-9]|[$-_@.&+]|[!*\(\),]|(?:%[0-9a-fA-F][0-9a-fA-F]))+

Конечно, такое выражение не определит все url'ы и, наоборот, не все строчки, распознаваемые таким регулярным выражением, являются url'ами. Но для многих практических задач такое решение приемлемо.

В языках программирования вы можете встретить дополнительные операции: диапазоны ([0-9]), опциональные символы ([s]?), непустые итерации (a+ — то же, что aa*, т.е. элемент повторяется не менее одного раза) и другие. Они служат лишь для получения более компактных записей, никак не влияя на то, какие в принципе языки можно описывать при помощи регулярных выражений.

Если же обходиться без дополнительных операций, регулярные выражения обычно записываются при помощи символов (в том числе цифр), знаков | (объединение), * (итерация) и скобок. Конкатенация специальным образом не выделяется, она выражается следованием символов друг за другом.

Например, запишем такое регулярное выражение:

$inline$

Оно описывает язык, состоящий из следующих строк:

abcde
abcdf
abcdef
abcdeef
abcdeeef
abcdeeeef

и так далее.

2. Конечные автоматы

Конечные автоматы являются ещё одним способом представления регулярных языков. Конечный автомат — это ориентированный конечный граф, дуги которого взвешены символами алфавита. Одна из вершин графа считается начальной, при этом несколько вершин могут считаться конечными (терминальными). Вершины этого графа называются состояниями автомата.

В начале обработки строки автомат находится в начальном состоянии. Далее он просматривает символы один за другим, осуществляя переходы между состояниями в соответствии с весами, размещёнными на дугах.

Если в определённый момент из состояния нет исходящей дуги, соответствующей текущему символу входной строки, автомат отклоняет строку. Если строка завершилась, а автомат не достиг терминального состояния, строка также отклоняется. Наконец, если по завершению входной строки автомат оказался в терминальном состоянии — строка считается принятой и принадлежащей языку, который описывается этим автоматом.

Описания языков в виде конечных автоматов эквивалентны описаниям в виде регулярных выражений. Для того, чтобы показать это, временно разрешим записывать на рёбрах конечного автомата регулярные выражения и будем считать, что переход по дуге влечёт за собой вычитывание последовательности символов, принимаемой этим регулярным выражением.

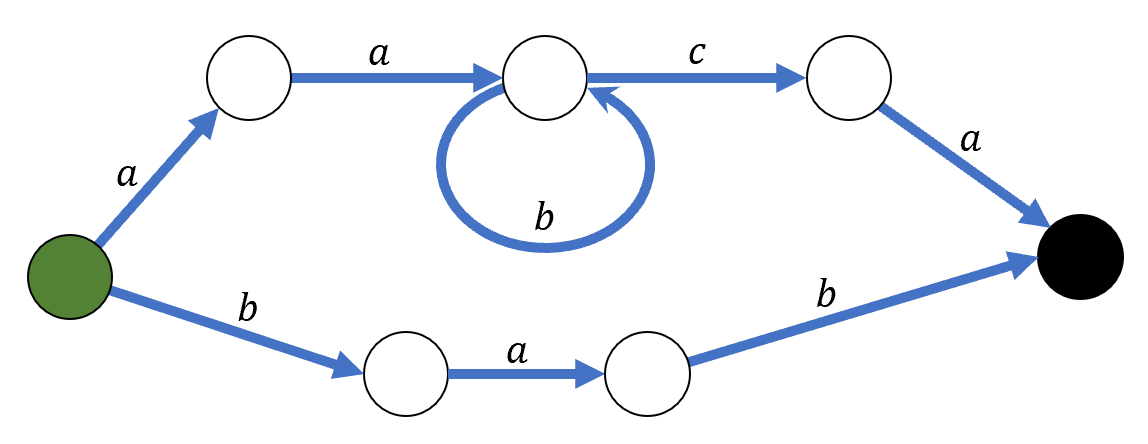
Пример конечного автомата, эквивалентного регулярному выражению $bab|aab^{*}ca$

Теперь будем по одной удалять состояния конечного автомата. Пусть $inline$ , $inline$ , $inline$ — вершины автомата. Из $inline$ можно попасть в $inline$ непосредственно, соответствующая дуга взвешена языком $L_{ik}$ . Аналогично, дуга из $inline$ в $inline$ взвешенна языком $L_{ij}$ , а из $inline$ в $inline$ — $L_{jk}$ . Нельзя забывать, что вершина $inline$ может иметь петлю, взвешенную языком $L_{jj}$ .

Удалим вершину $inline$ , а вершины $inline$ и $inline$ свяжем дугой, взвешенной языком

$L^{'}_{ik} = L_{ik} \cup L_{ij} \cdot L^{*}_{jj} \cdot L_{jk}$

Аналогичным образом установим веса дуг между всеми парами вершин, которые были связаны через $inline$ . После этого получим конечный автомат, содержащий на одну вершину меньше и при этом, очевидно, эквивалентный исходному.

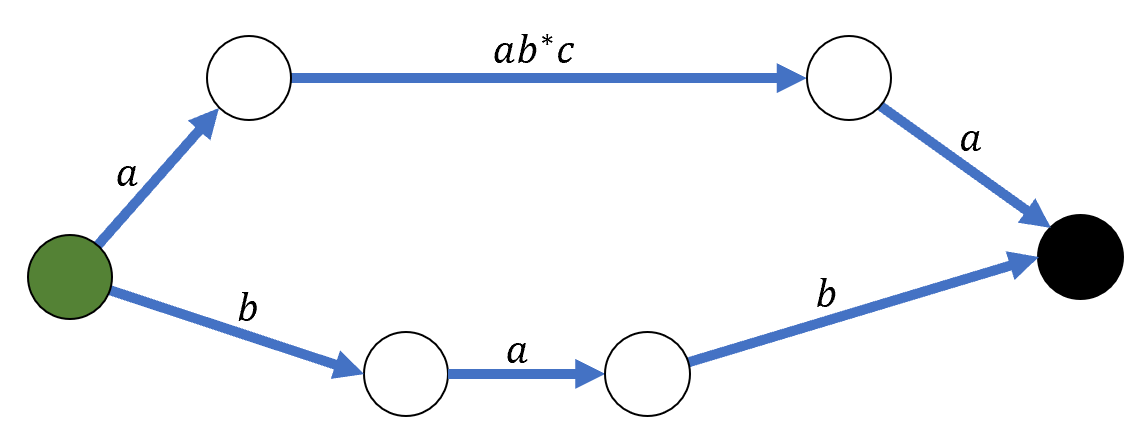
Удаление вершины с петлёй в конечном автомате из предыдущего примера

Удаляя так вершину за вершиной из исходного автомата, мы получим автомат, содержащий только начальную и несколько конечных вершин. Это не очень удобно, поэтому свяжем все терминальные вершины автомата с какой-нибудь одной из них дугами, взвешенными регулярным выражением $\varepsilon$ . Эта избранная терминальная вершина останется единственной терминальной вершиной модифицированного автомата, и тогда результатом удаления всех возможных вершин будет автомат с одной начальной вершиной и одной конечной вершиной. Они будут связаны дугой, вес которой и будет искомым регулярным выражением.

Обратно, можно построить конечный автомат по регулярному выражению. Конечные автоматы для тривиальных регулярных выражений построить просто: для пустого языка это будет конечный автомат без дуг; для языка, содержащего только пустое слово, это будет граф с одной вершиной, которая считается и начальной, и терминальной; для языка, содержащего одно однобуквенное слово, это будет граф, в котором единственная начальная вершина соединена с единственной терминальной вершиной дугой, взвешенной этим однобуквенным словом.

Далее, необходимо построить правила преобразования операций над регулярными языками к операциям над конечными автоматами. Эти правила могут выглядеть, например, так:

После применения этих правил останется только технично избавиться от дуг, взвешенных пустыми строками.

3. Лемма о разрастании для регулярных языков

Рассмотрим язык $L = \{a^nb^n | n \in \mathbb{N}_0 \}$ . Он содержит строки $\varepsilon$ , $inline$ , $inline$ , $inline$ и так далее. Является ли он регулярным? Представим себе, что да.

В таком случае соответствующий конечный автомат, очевидно, содержит хотя бы один цикл. В действительности понадобится, по всей видимости, два цикла: один для того, чтобы генерировать сколь угодно длинные последовательности из букв $inline$ и другой — для последовательностей из букв $inline$ . Как гарантировать, что циклы будут совершать равное число итераций? Ведь у конечного автомата нет памяти… Может быть, соответствующего конечного автомата не существует, а язык не является регулярным?

И действительно, не является! Интуитивное соображение, приведённое выше, можно перестроить строго математически. Результатом этого будет

Лемма о разрастании регулярных языков. Для любого регулярного языка $inline$ существует число $n \in \mathbb{N}$ такое, что $\forall w \in L, |w| \ge n$ найдутся такие три слова $inline$ , $inline$ , $inline$ , что: $inline$ ; $y \ne \varepsilon$ ; $|xy| \le n$ ; $\forall k \ge 0: xy^kz \in L$ .

Доказательство леммы

Пусть $inline$ — регулярный язык, которому соответствует конечный автомат с числом вершин $inline$ , а $w \in L$ — слово длины не менее $inline$ .

Рассмотрим последовательность вершин конечного автомата в порядке их посещения при разборе слова $inline$ : $inline$ , $inline$ , $inline$ , ..., $inline$ . Последовательность, очевидно, содержит $inline$ вершину, и $m \ge n$ .

Так как всего в графе только $inline$ вершин, хотя бы одна из них повторяется в последовательности. Пусть $inline$ — первая вершина последовательности из числа повторяющихся, причём второй раз она встретилась в позиции $inline$ . Тогда $inline$ — первые $inline$ символов строки $inline$ , $inline$ — отрезок $inline$ , соответствующий перемещению из $inline$ в $inline$ , а $inline$ — отрезок $inline$ , соответствующий перемещению из $inline$ в $inline$ .

Так как переход от $inline$ к $inline$ образует цикл в конечном автомате, по этому циклу можно пройти произвольное (в том числе и нулевое!) число раз, и всякий раз будет получаться строчка, принимаемая автоматом, поэтому $\forall k \in \mathbb{N}_0: xy^kz \in L$ .

При этом пара состояний $inline$ , $inline$ — первый повтор в рассматриваемой последовательности. Значит, все состояния $inline$ , $inline$ , ..., $a_{j-1}$ являются различными. Раз так, то их не больше $inline$ . Отсюда получаем, что $j \le n$ и $|xy| \le n$ , что и требовалось.

Другими словами: в любом достаточно длинном слове найдётся непустая, но не совпадающая со всем словом часть, которую можно повторять произвольное (в т.ч. нулевое) число раз, оставаясь при этом в рамках того же регулярного языка, что и исходное слово.

Попробуем применить эту лемму к языку $L = \{a^nb^n | n \in \mathbb{N}_0\}$ . Пусть $inline$ — то самое число из леммы для соответствующего регулярного языка. Тогда строку $inline$ можно представить в виде $inline$ ,
причём $|xy|\le n$ , а, значит, строка $inline$ содержит только символы $inline$ . Строка $inline$ поэтому тоже содержит только символы $inline$ , да ещё и является непустой согласно утверждению леммы. Тогда строки вида $inline$ для $inline$ будут содержать строго больше символов $inline$ , чем символов $inline$ и, стало быть, не принадлежат языку $inline$ . Но их принадлежность языку следует из леммы и условия регулярности $inline$ . Следовательно, $inline$ не является регулярным языком!

Аналогично можно доказать нерегулярность языка $inline$ , который является подмножеством множества всех правильных скобочных последовательностей. А вслед за ним нерегулярным оказывается и весь язык правильных скобочных последовательностей.

4. Контекстно-свободные грамматики

Грамматики — способ определения языков, основанный на операции постановки строки вместо подстроки.

Алфавит в грамматиках разбит на две части: терминальные символы (терминалы) $inline$ и нетерминальные символы (нетерминалы) $inline$ ; $\Sigma = N \cup T$ . Среди нетерминалов выделен специальный символ $S \in N$ — аксиома грамматики.

Ключевой частью грамматики являются правила вывода $inline$ . Правила вывода можно описать как бинарное отношение $\varphi$ на множестве строк в алфавите $\Sigma$ : если $(s_1, s_2) \in \varphi$ , то правилами грамматики разрешено заменять любое вхождение строки $inline$ на строку $inline$ . Это бинарное отношение можно воспринимать как многозначную функцию: для каждой левой части может быть определено несколько различных правых частей. Обычно, если $(s_1, s_2) \in \varphi$ , пишут просто $s_1 \rightarrow s_2$ .

Строка $\beta$ выводится за один шаг из строки $\alpha$ , если эти строки допускают представление в виде $\alpha = xs_1z$ , $\beta = xs_2z$ и при этом $(s_1, s_2) \in \varphi$ . То есть, вывод за один шаг — это замена подстроки в соответствии с правилами вывода. Будем это отношение обозначать так: $\alpha \vdash \beta$ .

Скажем, что строка $\beta$ выводится из строки $\alpha$ (за произвольное число шагов), если существует последовательнось строк $s_0 = \alpha$ , $inline$ , $inline$ , ..., $s_{k+1}=\beta$ , в которой каджая строка выводится за один шаг из предыдущей: $s_i \vdash s_{i+1}$ . В таком случае будем писать $\alpha \Rightarrow \beta$ .

Строка $inline$ допускается грамматикой, если она состоит только из терминальных символов и при этом выводится из аксиомы: $s \in T^*$ , $S \Rightarrow s$ . Язык, определяемый грамматикой, состоит из всех допускаемых ею строк.

Осталось добавить, что грамматика называется контекстно-свободной (КС-грамматикой), если все левые части правил вывода — единичные нетерминалы. Языки, описываемые контекстно-свободными грамматиками, называются контекстно-свободными языками.

Например, такая КС-грамматика описывает правильные скобочные последовательности:

$S \rightarrow (S)S$
$S \rightarrow \varepsilon$

И действительно, всякая правильная скобочная последовательность либо является пустой строкой, либо начинается с открывающей скобки. Если последовательность непустая, то где-то в ней встречается закрывающая скобка, парная первой открывающей. Между этими скобками находится правильная скобочная последовательность; после закрывающей скобки также находится правильная скобочная последовательность.

Чтобы лучше понять, как это работает, рассмотрим «наивную» реализацию поиска вывода строки в грамматике через поиск в ширину:

def BuildPath(queue, parents, parent):
    path = []
    while parents[parent] != parent:
        path += [queue[parent]]
        parent = parents[parent]
    return path[::-1]

def Solve(rules, target):
    queue = ['S']
    parents = [0]

    idx = 0
    while idx < len(queue):
        current = queue[idx]

        for rule in rules:
            entryIdx = current.find(rule[0])
            while entryIdx != -1:
                new = current[:entryIdx] + rule[1] + current[entryIdx + len(rule[0]):]

                if new == target:
                    path = [queue[0]] + BuildPath(queue, parents, idx) + [new]
                    return path

                queue.append(new)
                parents.append(idx)

                entryIdx = current.find(rule[0], entryIdx + 1)

        idx += 1

Такая реализация работает, конечно, очень медленно и, кроме того, вообще не завершает работу, если строка не выводится грамматикой; однако эта реализация вполне подходит для демонстрационных целей! Вот и в данном случае:

rules = [
    ("S", "(S)S"),
    ("S", ""),
]
target = "(()())()"
print('\n'.join(Solve(rules, target)))

S
(S)S
((S)S)S
((S)(S)S)S
((S)(S)S)(S)S
(()(S)S)(S)S
(()()S)(S)S
(()())(S)S
(()())()S
(()())()

Можно построить КС-грамматику и для языка $L = \{a^nb^n | n \in \mathbb{N}_0\}$ :

rules = [
    ("S", "aSb"),
    ("S", ""),
]
target = "aaabbb"
print('\n'.join(Solve(rules, target)))

S
aSb
aaSbb
aaaSbbb
aaabbb

Мы только что построили КС-грамматики для языков, которые ранее не смогли описать регулярными выражениями. Оказывается, регулярные языки эквивалентны подмножеству КС-грамматик, которое называется автоматными грамматиками. Таким образом, КС-грамматики выразительнее регулярных выражений: они позволяет описывать любые языки, являющиеся регулярными, но также и некоторые языки, регулярными не являющиеся.

Тем не менее, и КС-грамматики описывают не всё.

5. Лемма о разрастании для КС-грамматик

Рассмотрим язык $L = \{ a^nb^nc^n | n \in \mathbb{N}_0 \}$ . Мы уже знаем, что контекстно-свободные грамматики позволяют строить строки вида $inline$ , так что, видимо, надо будет сделать как-то так:

$S \rightarrow \varepsilon$
$S \rightarrow AB$
$A \rightarrow aAb$
$B \rightarrow Bc$
$A \rightarrow \varepsilon$
$B \rightarrow \varepsilon$

Такая грамматика построит язык $inline$ . Как же добиться, чтобы $inline$ всегда совпадало с $inline$ ? Ведь подстановки действуют локально и ничего «не знают» ни о строке в целом, ни о том, сколько раз были применены другие подстановки. И, действительно, добиться этого невозможно. Данный язык не является контекстно-свободным, и установить это позволяет

Лемма о разрастании контекстно-свободных грамматик. Для любого контекстно-свободного языка $inline$ существует число $n \in \mathbb{N}$ такое, что $\forall w \in L, |w| \ge n$ найдутся такие слова $inline$ , $inline$ , $inline$ , $inline$ , $inline$ , что: $inline$ ; $vy \ne \varepsilon$ ; $|vxy| \le n$ ; $\forall k \ge 0: uv^kxy^kz \in L$ .

Доказательство леммы

Для доказательства нам потребуется вначале привести грамматику к нормальной форме Хомского, воспользовавшись соответствующим алгоритмом.

В этой форме в правых частях правил вывода могут находиться либо два нетерминала, либо один терминал. Пустая строка может находиться в правой части, только если в левой находится аксиома. Итак, разрешены правила следующих трёх видов:
$S \rightarrow \varepsilon$
$A \rightarrow BC$
$A \rightarrow a$

Для каждой строки, выводимой в грамматике, можно построить дерево разбора согласно применяемым правилам: внутренними вершинами дерева являются нетерминалы, листьями — терминалы. Корнем деревая является аксиома. Ребра расставляются в соответствии с применяемыми правилами вывода.

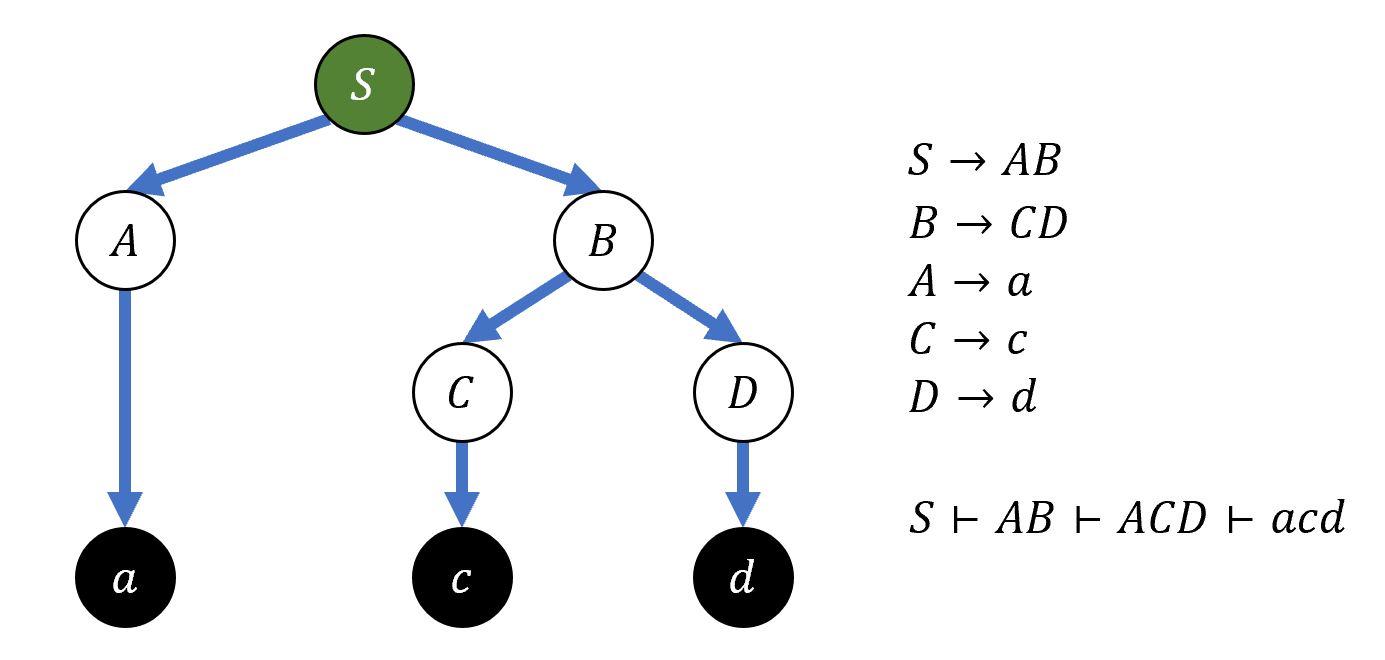
Пример КС-грамматики и дерева разбора для строки acd

Итак, пусть грамматика находится в нормальной форме. Выберем $n=2^{|N|+1}$ , где $inline$ — общее число нетерминалов в грамматике, и пусть $w \in L, |w| \ge n$ . Тогда для этого слова можно построить дерево разбора. Дерево разбора — бинарное, т.к. грамматика находится в нормальной форме. Значит, высота дерева $inline$ не может быть меньше, чем $inline$ . Эта высота является числом нетерминалов, которые встречаются на пути из корня дерева до одного из листов-терминалов. Раз число нетерминалов в этом пути превосходит число различных нетерминалов в грамматике, как минимум один из них повторяется.

Выберем в графе вершину с нетерминалом $inline$ таким образом, чтобы в поддереве этой вершины все нетерминалы были различны и не повторялись, но при этом в нём встречался бы нетерминал $inline$ . Такую вершину обязательно можно будет выбрать: хотя бы один повторяющийся нетерминал в дереве есть, а из всех повторяющихся нетерминалов можно выбрать тот, что находится на наибольшем возможном расстоянии от корня.

Нетерминал $inline$ встречается в дереве разбора, поэтому существует вывод $S \vdash uBz$ . $inline$ также встречается в поддереве, в корне которого записан сам нетерминал $inline$ , поэтому существует вывод $B \rightarrow vBy$ , причём $vy \ne \varepsilon$ , т.к. в нормальной форме нетерминал порождает как минимум два нетерминала, каждый из которых затем превращается как минимум в один терминал. Последнее вхождение $inline$ порождает некоторую строку $inline$ .

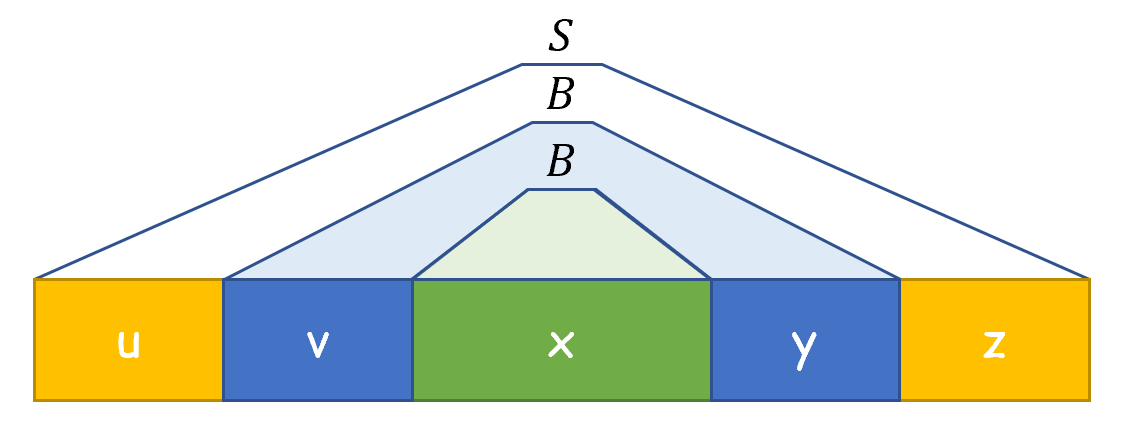
Итого:

$S \vdash uBz$
$B \vdash vBy$
$B \vdash x$

Значит, $\forall k \in \mathbb{N}_0 S \vdash uv^kxy^kz$ , причём $vy \ne \varepsilon$ .

Осталось лишь получить ограничение на длину строки $inline$ . Т.к. эта строка выводится из поддерева нетерминала $inline$ , а в этом дереве нет повторяющихся нетерминалов, высота дерева ограничена общим числом нетерминалов $inline$ . Значит, полученная строка не может иметь длину больше чем $2^{|N|+1} = n$ . Так что $|vxy| \le n$ .

Применим эту лемму к языку $L = \{ a^nb^nc^n | n \in \mathbb{N}_0\}$ . Предположим, что он является контекстно-свободным. Тогда выполнена лемма о разрастании, и пусть $inline$ — то самое число из леммы. Рассмотрим слово $inline$ .

Для него выполнено утверждение леммы, так что $inline$ , причём $|vxy| \le n$ и $vy \ne \varepsilon$ , и все строки вида $inline$ также принадлежат рассматриваемому языку.

Строка $inline$ не является пустой и не содержит хотя бы один из символов $inline$ , $inline$ , т.к. в строке $inline$ между последовательностями символов $inline$ и $inline$ расположена последовательность из $inline$ букв $inline$ , а длина $inline$ не превосходит $inline$ .

Поэтому количество вхождений хотя бы одного из символов в строки вида $inline$ не будет увеличиваться с ростом $inline$ . Значит, для $inline$ не найдётся такого $inline$ , что $inline$ , и такие строки не относятся к языку $inline$ . Следовательно, он не является контекстно-свободным!

6. Грамматики общего вида

Что же, теперь терпеливый читатель умеет доказывать ограниченность регулярных и контекстно-свободных языков. В качестве завершения продемонстрирую, как построить язык $L = \{ a^nb^nc^n | n \in \mathbb{N}_0 \}$ , используя грамматику общего вида.

Начнём с правил для аксиомы грамматики:

$S \rightarrow \varepsilon$
$S \rightarrow aHbCE$

Нетерминал $inline$ будет указывать, где находится граница между группами из символов $inline$ и $inline$ . Поэтому в конечном счёте его достаточно превращать в пустую строку:

$E \rightarrow \varepsilon$

Нетерминал $inline$ обеспечивает строительство строк неограниченной длины:

$H \rightarrow aHbC$
$H \rightarrow \varepsilon$

Наконец, нужно обеспечить, чтобы нетерминалы $inline$ перемещались в правый участок строки и там превращались в терминалы $inline$ . Тут-то и пригодятся правила со сложными левыми частями!

$Cb \rightarrow bC$
$CE \rightarrow Ec$

Вот и всё! Применяя программу из пункта 5 к этим правилам вывода, получим:

rules = [
    ("S", "aHbCE"),
    ("H", ""),
    ("H", "aHbC"),
    ("Cb", "bC"),
    ("CE", "Ec"),
    ("E", ""),
]
target = "aaabbbccc"
print('\n'.join(Solve(rules, target)))

S
aHbCE
aaHbCbCE
aaaHbCbCbCE
aaaHbbCCbCE
aaaHbbCbCCE
aaaHbbbCCCE
aaaHbbbCCEc
aaaHbbbCEcc
aaaHbbbEccc
aaaHbbbccc
aaabbbccc

У получившегося алгоритма есть интересная особенность: правила со сложной левой частью позволяют как бы «перемещать» группы символов; в данном случае нетерминалы $inline$ перемещаются в правую часть строки. Похожий паттерн часто встречается в алгоритмах для машин Тьюринга.

Он же используется при доказательстве эквивалентности (в некотором не самом простом смысле) машин Тьюринга и ассоциативных исчислений, основанных на грамматиках. Об этом расскажу как-нибудь в другой раз.

Теги:

Хабы: