Или старое доброе динамическое программирование без этих ваших нейросетей.
Полтора года назад мне довелось участвовать в корпоративном конкурсе (с целью развлечения) в написании бота для игры Lode Runner. 20 лет назад я прилежно решал все задачи на динамическое программирование в соответствующем курсе, но изрядно все подзабыл и не имел опыта программирования игровых ботов. Времени было выделено мало, пришлось вспоминать, экспериментировать на ходу и самостоятельно наступать на грабли. Но, внезапно, все получилось очень неплохо, так что я решил как-то систематизировать материал и при этом не утопить читателя матаном.
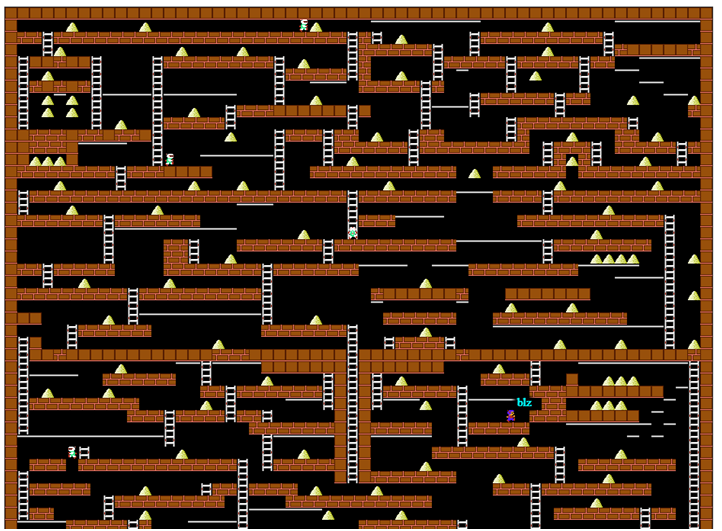
Экран игры с сервера проекта Codenjoy
Для начала немного опишем правила игры: игрок перемещается по горизонтали по полу или по трубам, умеет лазить вверх и вниз по лестницам, падает, если под ним не оказывается пола. Так же он может прорубать яму слева или справа от себя, но не каждую поверхность можно прорубить – условно «деревянный» пол можно, а бетонный – нельзя.
Монстры бегают за игроком, падают в прорубленные ямы и помирают в них. Но самое главное – игрок должен собирать золото, за первое собранное золото он получает 1 балл профита, за N-е он получает N баллов. После гибели общий профит сохраняется, но за первое золото снова дают 1 балл. Это наводит на мысль, что главное – оставаться в живых как можно дольше, а уж собирать золото – как-то вторично.
Поскольку на карте есть места, из которых игрок не может выбраться сам, то в игру было введено бесплатное самоубийство, которое рандомно помещало игрока куда-то, но по факту сломало всю игру – самоубийство не прерывало рост стоимости найденного золота. Но мы не будем злоупотреблять этой особенностью.
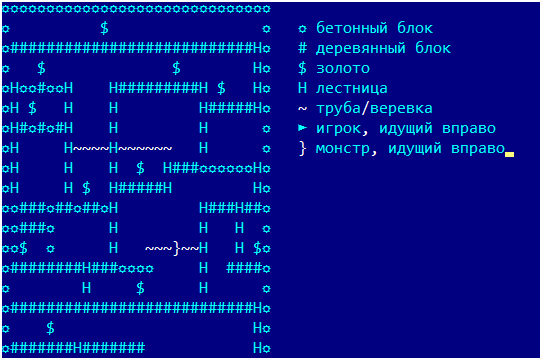
Все примеры из игры будут даваться в упрощенном отображении, которое использовалось в логах программы:
Чтобы реализовать бота с помощью какой-либо математики нам надо задать какую-то целевую функцию, описывающую достижения бота и найти ему действия, которые ее максимизируют. Например, за сбор золота мы получим +100, за смерть -100500, таким образом, никакой сбор золота не перебьет возможную смерть.
Отдельный вопрос, а на чем именно мы определяем целевую функцию, т.е. что вообще является состоянием игры? В простейшем случае достаточно координат игрока, но в нашем все гораздо сложнее:
Выглядит страшно. Потому давайте немного упростим задачу и пока не будет запоминать съеденное золото (в дальнейшем вернемся к этому), так же не будем запоминать координаты других игроков и монстров.
Таким образом, текущее состояние игры это:
Действия игрока изменяют состояние понятным образом:
Теперь нам надо понять, а как собственно максимизировать функцию. Одним из почтенных классических методов, позволяющих просчитать игру на N ходов вперед является динамическое программирование. Совсем без формул обойтись не получится, потому дам их в упрощенном виде. Сначала придется ввести много обозначений.
Для простоты отчет времени будем вести от текущего хода, т.е. текущий ход это t=0.
Обозначим состояние игры на ходе t через .
.
Множество будет обозначать все допустимые действия бота (при конкретном состоянии, но для простоты индекс состояния писать не будем), через
будет обозначать все допустимые действия бота (при конкретном состоянии, но для простоты индекс состояния писать не будем), через  обозначим конкретное действие на ходе t (индекс опустим).
обозначим конкретное действие на ходе t (индекс опустим).
Состояние под действием
под действием  переходит в состояние
переходит в состояние  .
.
Выигрыш при совершении действия a в состоянии обозначим его как
обозначим его как  . При его вычислении будем считать, что если мы съели золото, то он равен G=100, если погибли, то D=-100500, иначе 0.
. При его вычислении будем считать, что если мы съели золото, то он равен G=100, если погибли, то D=-100500, иначе 0.
Пусть это функция выигрыша при оптимальной игре бота, находящегося в момент времени t в состоянии x. Тогда нам просто надо найти действие, которое максимизирует
это функция выигрыша при оптимальной игре бота, находящегося в момент времени t в состоянии x. Тогда нам просто надо найти действие, которое максимизирует  .
.
Теперь запишем первую формулу, очень важную и при этом почти правильную:
Или для произвольного момента времени
Выглядит довольно коряво, но смысл простой — оптимальное решение на текущий ход состоит из оптимального решения за следующий ход и выигрыша на текущем ходе. Это криво сформулированный принцип оптимальности Беллмана. Мы пока ничего не знаем об оптимальных значениях на шаге 1, но если бы они были нам известны, то мы нашли бы действие, которое максимизирует функцию простым перебором по всем действиям бота. Красота рекуррентных соотношений в том, что мы можем найти , применив к нему принцип оптимальности, выразив его точно такой же формулой через
, применив к нему принцип оптимальности, выразив его точно такой же формулой через  . Так же легко мы можем выразить функцию выигрыша на любом шаге.
. Так же легко мы можем выразить функцию выигрыша на любом шаге.
Казалось бы, задача решена, но тут мы сталкиваемся с проблемой, что если на каждом шаге нам надо было перебирать 6 действий игрока, то на N шаге рекурсии нам придется перебирать 6^N вариантов, что для N=8 уже вполне приличное число ~1.6 млн случаев. С другой стороны, у нас есть гигагерцовые микропроцессоры, которым нечем заняться и кажется, что они с задачей вполне справятся, а мы ограничим им глубину перебора именно 8 ходами.
И так, наш горизонт планирования равен 8 ходам, но откуда взять значения ? И тут мы просто придумываем, что мы умеем как-то анализировать перспективность позиции, и припишем ей какую-то ценность, исходя их высших соображений. Пусть
? И тут мы просто придумываем, что мы умеем как-то анализировать перспективность позиции, и припишем ей какую-то ценность, исходя их высших соображений. Пусть  , где
, где  это функция стратегии, в самом простом варианте это просто матрица, из которой мы выбираем значение по геометрическим координатам бота. Можно сказать, что первые 8 ходов это была тактика, а дальше начинается стратегия. На самом деле никто не ограничивает нас в выборе стратегии, и мы займемся ей позже, а пока, дабы не уподобляться сове из анекдота про зайцев и ежиков, перейдем к тактике.
это функция стратегии, в самом простом варианте это просто матрица, из которой мы выбираем значение по геометрическим координатам бота. Можно сказать, что первые 8 ходов это была тактика, а дальше начинается стратегия. На самом деле никто не ограничивает нас в выборе стратегии, и мы займемся ей позже, а пока, дабы не уподобляться сове из анекдота про зайцев и ежиков, перейдем к тактике.
И так, мы определились с алгоритмом. На каждом шаге решаем оптимизационную задачу, находим оптимальное действие для шага, совершаем его, после чего игра переходит к следующему шагу.
Решать новую задачу на каждом шаге необходимо, потому с каждым ходом игры задача немного изменяется, появляется новое золото, кто-то кого-то съедает, игроки перемещаются…
Но не стоит думать, что наш гениальный алгоритм может предусмотреть все. После решения оптимизационной задачи нужно обязательно добавить обработчик, который проверит неприятные ситуации:
Все это может потребовать радикальной смены стратегии, самоубийства или каких-то других действий за рамками оптимизирующего алгоритма. Природа этих ситуаций может быть разной. Иногда противоречия между стратегией и тактикой приводят к зависанию бота на месте в точке, которая ему кажется стратегически важной, что было открыто античными ботописателями под названием Буриданов Осел.

Ваши противники могут зависать и закрывать вам короткую дорогу к вожделенному золоту – все это мы разберем позже.
Рассмотрим простой случай, когда справа от бота расположено одно золото и в радиусе 8 клеток золота больше нет. Какой шаг сделает бот, руководствуясь нашей формулой? На самом деле – совершенно любой. К примеру, все перечисленные решения дают совершенно одинаковый результат даже на три хода:
Все три варианта дают один выигрыш равный 100, бот может выбрать вариант с бездействием, на следующем шаге снова решить ту же задачу, снова выбрать бездействие… И стоять на месте вечно. Нам надо модифицировать формулу расчета выигрыша, чтобы стимулировать бота действовать как можно раньше:
мы умножили будущий выигрыш на следующем шаге на «инфляционный коэффициент» E, который нужно выбирать меньше 1. Можно смело экспериментировать со значениями 0.95 или 0.9. Но не выбирайте его слишком малым, например, при значении E= 0.5 золото, съеденное на 8 ходе, принесет всего 0,39 балла.
И так, мы переоткрыли принцип «Не откладывай на завтра то, что можно съесть сегодня».
Сбор золота это конечно хорошо, но надо еще подумать над безопасностью. У нас две задачи:
Но мы не говорим боту что надо делать, мы задаем значение функции профита и оптимизирующий алгоритм сам выберет подходящие шаги. Отдельная проблема состоит в том, что мы не просчитываем точно, где может оказаться монстр на конкретном ходе. Потому для простоты, будем считать, что монстры стоят на месте, а нам просто не надо к ним подходить.
Если они начнут к нам подходить – бот сам начнет убегать от них, потому что его будут штрафовать за слишком близкое нахождения с ними (этакая самоизоляция). И так, вводим два правила:
Понятие «подошли к монстру на расстояние d» мы раскроем чуть позже, а пока перейдем к стратегии.
Математически задача оптимального обхода золота является давно решенной задачей коммивояжера, решение которой не доставляет удовольствия. Но прежде чем решать подобные задачи, надо задуматься над простым вопросом – а как вообще найти расстояние между двумя точками в игре? Или чуть в более полезной форме: для данного золота и для любой точки карты найти минимальное количество ходов, за которое игрок дойдет из точки до золота. Забудем на какое-то время про копание ям и прыганье в них, оставим только естественные перемещения на 1 клетку. Только ходить мы будем в обратную сторону – от золота и по всей карте.

На первом шаге выберем все клетки, из которых можно за один ход попасть в золото и припишем им 1. На втором шаге, выберем все клетки, из которых за один шаг попадаем в единички и припишем им 2. На картинке изображен случай для 3х шагов. А теперь попробуем записать это все формально, в виде пригодном для программирования.
Нам потребуются:
То же самое в псевдокоде:
На выходе алгоритма у нас будет карта distance со значением расстояния от каждой точки всего поля игры до золота. При этом для точек, из которых золото недостижимо, значение distance равно -1. Математики называют подобный обход поля игры (которое образует граф с вершинами в точках поля и ребрами, соединяющими доступными за один ход вершины) «обход графа в ширину». Если бы мы реализовали рекурсию, а не два массива границ, то это называлось бы «обход графа в глубину», но поскольку глубина может быть достаточно большой (несколько сотен), я советую избегать при обходе графов рекурсивных алгоритмов.
Реальный алгоритм будет чуть сложнее из-за копания ямы и прыжка в нее – получается, что за 4 хода мы перемещаемся на одну клетку вбок и на две вниз (поскольку движение в обратную сторону, то вверх), но легкая модификация алгоритма решает проблему.
Я дополнил картинку цифрами, в том числе с учетом копания ямы и прыжка в нее:

Что нам это напоминает?

Запах золота! И наш бот пойдет на этот запах, как Рокки на сыр (но при этом он не лишается мозгов и уворачивается от монстров, и даже копает им ямы). Давайте составим для него простую жадную стратегию:
Где это некоторая воображаемая ценность золота, желательно чтобы оно ценилось в несколько раз меньше настоящего, а
это некоторая воображаемая ценность золота, желательно чтобы оно ценилось в несколько раз меньше настоящего, а  это инфляционный коэффициент <1, потому что чем дальше воображаемое золото находится, тем дешевле оно стоит. Соотношение коэффициентов E и
это инфляционный коэффициент <1, потому что чем дальше воображаемое золото находится, тем дешевле оно стоит. Соотношение коэффициентов E и  составляет нерешенную проблему тысячелетия и оставляет простор для творчества.
составляет нерешенную проблему тысячелетия и оставляет простор для творчества.
Не стоит думать, что наш бот всегда будет бегать к ближайшему золоту. Допустим слева на расстоянии 5 клеток у нас одно золото и далее пустота, а справа два золота на расстоянии 6 и 7. Поскольку реальное золото ценнее воображаемого, бот пойдет вправо.
Прежде чем перейти к более интересным стратегиям, сделаем еще одно улучшение. В игре гравитация тянет игрока вниз, а вверх он может подниматься только по лестницам. А значит, золото, которое находится выше, должно цениться выше. Если высота отчитывается от верхней линии вниз, тогда можно умножить ценность золота (с вертикальной координатой y) на величину . Для коэффициента
. Для коэффициента  был придуман новый термин «коэффициент вертикальной инфляции», по крайней мере, он не используется экономистами и хорошо отражает суть.
был придуман новый термин «коэффициент вертикальной инфляции», по крайней мере, он не используется экономистами и хорошо отражает суть.
С одним золотом разобрались, нужно что-то делать со всем золотом, причем не хотелось бы привлекать тяжелую математику. Есть очень элегантное, простое и неправильное (в строгом смысле) решение – если одно золото создает вокруг себя «поле» ценности, то давайте просто сложим все поля ценности от всех клеток с золотом в одну матрицу и используем ее как стратегию. Да, это не оптимальное решение, но несколько единиц золота на средней дистанции могут оказаться ценнее, чем одно близкое.
Однако новое решение порождает новые проблемы – новая матрица ценности может содержать локальные максимумы, вблизи которых золота нет. Потому наш бот может в них попасть и не захочет выходить – значит надо добавить обработчик, проверяющий, что бот оказался в локальном максимуме стратегии и по итогам хода остался на месте. И теперь у нас есть инструмент для борьбы с зависаниями – отменить на N ходов такую стратегию и временно вернуться к стратегии ближайшего золота.
Довольно забавно наблюдать, как застрявший бот меняет стратегию и начинает непрерывно спускаться вниз, съедая все ближайшее золото, на нижних этажах карты бот приходит в себя и пытается вылезти наверх. Этакий доктор Джекил и мистер Хайд.
Вот наш бот подходит к золоту под полом:

Оно уже попадает в оптимизирующий алгоритм, осталось сделать 3 шага право, прорубить яму справа и прыгнуть в нее, а далее гравитация сделает все сама. Примерно вот так:

Но бот зависает на месте. Отладка показала, что никакой ошибки нет: бот решил, что оптимальной стратегией является подождать один ход, а потом пройти по указанному маршруту и на последнем анализируемом шаге взять золото. В первом случае он получает выигрыш от полученного золота и выигрыш от воображаемого золота (на последней анализируемой итерации он находится как раз в клетке, где было золото), а во втором – только от настоящего золота (хотя и на ход раньше), а вот выигрыша от стратегии уже нет, потому что место под золотом тухлое и не перспективное. Ну а на следующем ходе он снова решает передохнуть один ход, подобные проблемы мы уже разбирали.
Пришлось модифицировать стратегию – поскольку мы запоминали все золото, которое было съедено на этапе анализа, то из суммарной матрицы стратегической ценности делалось вычитания карт ценности съеденного золота, таким образом, стратегия учитывала достижение тактики (можно было по-другому считать ценность – складывая матрицы только для целого золота, но это вычислительно сложнее, потому что золота на карте намного больше, чем мы можем съесть за 8 ходов).
Но на этом наши мучения не закончились. Допустим, что матрица стратегической ценности имеет локальный максимум и бот подошел к нему на 7 ходов. Будет ли бот идти к нему, чтобы зависнуть? Нет, потому что для любого маршрута, в котором бот за 8 ходов попадет в локальный максимум, выигрыш будет одинаковым. Старая добрая прокрастинация. Причина которой состоит в том, что стратегический выигрыш никак не зависит от момента, в котором мы окажемся в клетке. Первое что приходит в голову – штрафовать бота за простой, но это никак не помогает от бессмысленного хождения влево/вправо. Надо лечить корневую причину – учитывать стратегический выигрыш на каждом ходу (как разницу между стратегической ценностью нового и текущего состояний), уменьшая его со временем на множитель.
Т.е. ввести в выражение для выигрыша дополнительное слагаемое:
значение целевой функции на последнем вообще брать нулевым: . Поскольку выигрыш обесценивается с каждым ходом умножением на коэффициент, это заставит нашего бота быстрее набирать стратегический выигрыш и устранит наблюдаемую проблему.
. Поскольку выигрыш обесценивается с каждым ходом умножением на коэффициент, это заставит нашего бота быстрее набирать стратегический выигрыш и устранит наблюдаемую проблему.
Данную стратегию я не проверял на практике, но выглядит многообещающе.
В этом случае желательно сделать близкой стоимость реального и стоимость воображаемого золота, чтобы бот не кидался в подвал к ближайшему золоту.
После того, как мы научились «растекаться» по карте, давайте проведем подобное «растекание» от каждого монстра на несколько ходов и найдем все клетки, в которых монстр может оказаться, вместе с числом ходов, за которое он это сделает. Это позволит игроку проползать по трубе над головой монстра совершенно безопасно.
И последний момент – при расчете стратегии и воображаемой ценности золота мы не учитывали положение остальных игроков, просто «стирая» их при анализе карты. Оказывается, что отдельные зависшие оболтусы могут перекрыть собой доступ к целым регионам, потому был добавлен дополнительный обработчик – отслеживать зависающих противников и при анализе замещать их на бетонные блоки.
Поскольку основной алгоритм – рекурсивный, то надо уметь быстро изменять объекты состояния и возвращать их исходное для дальнейшей модификации. Я использовал java, язык со сборкой мусора, перебор миллионов изменений, связанных созданием короткоживущих объектов, может вызывать несколько сборок мусора за один ход игры, что может стать фатальным с точки зрения быстродействия. Потому надо быть крайне осторожным в используемых структурах данных, я применял только массивы и списки. Ну или использовать проект Валгала на свой страх и риск :)
Исходный код можно найти тут на гитхабе. Не судите строго, многое было сделано на скорую руку. Игровой сервер проекта codenjoy обеспечит инфраструктуру для запуска ботов и наблюдения за игрой. На момент создания актуальной была ревизия использовалась ревизия 1.0.26.
Запускать сервер можно следующей строкой:
Сам проект крайне любопытный, обеспечивает играми на любой вкус.
Если вы все это дочитали до конца без предварительной подготовки и все поняли — то вы редкий молодец.
Полтора года назад мне довелось участвовать в корпоративном конкурсе (с целью развлечения) в написании бота для игры Lode Runner. 20 лет назад я прилежно решал все задачи на динамическое программирование в соответствующем курсе, но изрядно все подзабыл и не имел опыта программирования игровых ботов. Времени было выделено мало, пришлось вспоминать, экспериментировать на ходу и самостоятельно наступать на грабли. Но, внезапно, все получилось очень неплохо, так что я решил как-то систематизировать материал и при этом не утопить читателя матаном.

Экран игры с сервера проекта Codenjoy
Для начала немного опишем правила игры: игрок перемещается по горизонтали по полу или по трубам, умеет лазить вверх и вниз по лестницам, падает, если под ним не оказывается пола. Так же он может прорубать яму слева или справа от себя, но не каждую поверхность можно прорубить – условно «деревянный» пол можно, а бетонный – нельзя.
Монстры бегают за игроком, падают в прорубленные ямы и помирают в них. Но самое главное – игрок должен собирать золото, за первое собранное золото он получает 1 балл профита, за N-е он получает N баллов. После гибели общий профит сохраняется, но за первое золото снова дают 1 балл. Это наводит на мысль, что главное – оставаться в живых как можно дольше, а уж собирать золото – как-то вторично.
Поскольку на карте есть места, из которых игрок не может выбраться сам, то в игру было введено бесплатное самоубийство, которое рандомно помещало игрока куда-то, но по факту сломало всю игру – самоубийство не прерывало рост стоимости найденного золота. Но мы не будем злоупотреблять этой особенностью.
Все примеры из игры будут даваться в упрощенном отображении, которое использовалось в логах программы:

Немного теории
Чтобы реализовать бота с помощью какой-либо математики нам надо задать какую-то целевую функцию, описывающую достижения бота и найти ему действия, которые ее максимизируют. Например, за сбор золота мы получим +100, за смерть -100500, таким образом, никакой сбор золота не перебьет возможную смерть.
Отдельный вопрос, а на чем именно мы определяем целевую функцию, т.е. что вообще является состоянием игры? В простейшем случае достаточно координат игрока, но в нашем все гораздо сложнее:
- координаты самого игрока
- координаты всех ям, пробитых всеми игроками
- координаты всего золота на карте (или координаты съеденного недавно золота)
- координаты всех остальных игроков
Выглядит страшно. Потому давайте немного упростим задачу и пока не будет запоминать съеденное золото (в дальнейшем вернемся к этому), так же не будем запоминать координаты других игроков и монстров.
Таким образом, текущее состояние игры это:
- координаты самого игрока
- координаты всех ям
Действия игрока изменяют состояние понятным образом:
- Команды движения изменяют одну из соответствующих координат
- Команда копания ямы добавляют одну новую яму
- Падение игрока без опоры уменьшает вертикальную координату
- Бездействие стоящего на опоре игрока не изменяет состояние
Теперь нам надо понять, а как собственно максимизировать функцию. Одним из почтенных классических методов, позволяющих просчитать игру на N ходов вперед является динамическое программирование. Совсем без формул обойтись не получится, потому дам их в упрощенном виде. Сначала придется ввести много обозначений.
Для простоты отчет времени будем вести от текущего хода, т.е. текущий ход это t=0.
Обозначим состояние игры на ходе t через
Множество
Состояние
Выигрыш при совершении действия a в состоянии
Пусть
Теперь запишем первую формулу, очень важную и при этом почти правильную:
Или для произвольного момента времени
Выглядит довольно коряво, но смысл простой — оптимальное решение на текущий ход состоит из оптимального решения за следующий ход и выигрыша на текущем ходе. Это криво сформулированный принцип оптимальности Беллмана. Мы пока ничего не знаем об оптимальных значениях на шаге 1, но если бы они были нам известны, то мы нашли бы действие, которое максимизирует функцию простым перебором по всем действиям бота. Красота рекуррентных соотношений в том, что мы можем найти
Казалось бы, задача решена, но тут мы сталкиваемся с проблемой, что если на каждом шаге нам надо было перебирать 6 действий игрока, то на N шаге рекурсии нам придется перебирать 6^N вариантов, что для N=8 уже вполне приличное число ~1.6 млн случаев. С другой стороны, у нас есть гигагерцовые микропроцессоры, которым нечем заняться и кажется, что они с задачей вполне справятся, а мы ограничим им глубину перебора именно 8 ходами.
И так, наш горизонт планирования равен 8 ходам, но откуда взять значения
Общая схема
И так, мы определились с алгоритмом. На каждом шаге решаем оптимизационную задачу, находим оптимальное действие для шага, совершаем его, после чего игра переходит к следующему шагу.
Решать новую задачу на каждом шаге необходимо, потому с каждым ходом игры задача немного изменяется, появляется новое золото, кто-то кого-то съедает, игроки перемещаются…
Но не стоит думать, что наш гениальный алгоритм может предусмотреть все. После решения оптимизационной задачи нужно обязательно добавить обработчик, который проверит неприятные ситуации:
- Стояние бота на месте длительное время
- Постоянное хождение влево-вправо
- Слишком долгое отсутствие дохода
Все это может потребовать радикальной смены стратегии, самоубийства или каких-то других действий за рамками оптимизирующего алгоритма. Природа этих ситуаций может быть разной. Иногда противоречия между стратегией и тактикой приводят к зависанию бота на месте в точке, которая ему кажется стратегически важной, что было открыто античными ботописателями под названием Буриданов Осел.

Ваши противники могут зависать и закрывать вам короткую дорогу к вожделенному золоту – все это мы разберем позже.
Борьба с прокрастинацией
Рассмотрим простой случай, когда справа от бота расположено одно золото и в радиусе 8 клеток золота больше нет. Какой шаг сделает бот, руководствуясь нашей формулой? На самом деле – совершенно любой. К примеру, все перечисленные решения дают совершенно одинаковый результат даже на три хода:
- шаг влево – шаг вправо – шаг вправо
- шаг вправо – бездействие – бездействие
- бездействие – бездействие – шаг вправо
Все три варианта дают один выигрыш равный 100, бот может выбрать вариант с бездействием, на следующем шаге снова решить ту же задачу, снова выбрать бездействие… И стоять на месте вечно. Нам надо модифицировать формулу расчета выигрыша, чтобы стимулировать бота действовать как можно раньше:
мы умножили будущий выигрыш на следующем шаге на «инфляционный коэффициент» E, который нужно выбирать меньше 1. Можно смело экспериментировать со значениями 0.95 или 0.9. Но не выбирайте его слишком малым, например, при значении E= 0.5 золото, съеденное на 8 ходе, принесет всего 0,39 балла.
И так, мы переоткрыли принцип «Не откладывай на завтра то, что можно съесть сегодня».
Безопасность
Сбор золота это конечно хорошо, но надо еще подумать над безопасностью. У нас две задачи:
- Научить бота копать ямы, если монстр в походящей позиции
- Научить бота убегать от монстров
Но мы не говорим боту что надо делать, мы задаем значение функции профита и оптимизирующий алгоритм сам выберет подходящие шаги. Отдельная проблема состоит в том, что мы не просчитываем точно, где может оказаться монстр на конкретном ходе. Потому для простоты, будем считать, что монстры стоят на месте, а нам просто не надо к ним подходить.
Если они начнут к нам подходить – бот сам начнет убегать от них, потому что его будут штрафовать за слишком близкое нахождения с ними (этакая самоизоляция). И так, вводим два правила:
- Если мы подошли к монстру на расстояние d причем d<=3, то на нас налагается штраф 100500*(4-d)/4
- Если монстр подошел достаточно близко, находится на одной линии с нами и между нами есть яма, то мы получаем некоторый профит P
Понятие «подошли к монстру на расстояние d» мы раскроем чуть позже, а пока перейдем к стратегии.
Обходим графы
Математически задача оптимального обхода золота является давно решенной задачей коммивояжера, решение которой не доставляет удовольствия. Но прежде чем решать подобные задачи, надо задуматься над простым вопросом – а как вообще найти расстояние между двумя точками в игре? Или чуть в более полезной форме: для данного золота и для любой точки карты найти минимальное количество ходов, за которое игрок дойдет из точки до золота. Забудем на какое-то время про копание ям и прыганье в них, оставим только естественные перемещения на 1 клетку. Только ходить мы будем в обратную сторону – от золота и по всей карте.

На первом шаге выберем все клетки, из которых можно за один ход попасть в золото и припишем им 1. На втором шаге, выберем все клетки, из которых за один шаг попадаем в единички и припишем им 2. На картинке изображен случай для 3х шагов. А теперь попробуем записать это все формально, в виде пригодном для программирования.
Нам потребуются:
- Двумерный числовой массив distance [x,y], в котором будем хранить результат. Изначально для координат золота он содержит 0, для остальных точек -1.
- Массив oldBorder, в котором будем хранить точки, от которых мы будем двигаться, изначально в нем одна точка с координатами золота
- Массив newBorder, в котором будем хранить точки, найденные на текущем шаге
- Для каждой точки p из oldBorder находим все точки p_a, из которых можно за один шаг дойти до p (точнее просто сделаем все возможные шаги из p в обратном направлении, например, полет вверх при отсутствии опоры) причем distance [p_a]=-1
- Поместим каждую такую точку p_a в массив newBorder, в distance [p_a] запишем номер итерации
- После того как все точки пройдены:
- Меняем местами массивы oldBorder и newBorder, после чего очищаем newBorder
- Если oldBorder пуст, тогда заканчиваем алгоритм, иначе переходим в шагу 1.
То же самое в псевдокоде:
iter=1; newBorder.clear(); distance.fill(-1); distance[gold]=0; oldBorder.push(gold); while(oldBorder.isNotEmpty()) { for (p: oldBorder){ for (p_a: backMove(p)) { if (distance[p_a]==-1) { newBorder.push(p_a); distance[p_a]=iter; } } } Swap(newBorder, oldBorder); newBorder.clear(); iter++; }
На выходе алгоритма у нас будет карта distance со значением расстояния от каждой точки всего поля игры до золота. При этом для точек, из которых золото недостижимо, значение distance равно -1. Математики называют подобный обход поля игры (которое образует граф с вершинами в точках поля и ребрами, соединяющими доступными за один ход вершины) «обход графа в ширину». Если бы мы реализовали рекурсию, а не два массива границ, то это называлось бы «обход графа в глубину», но поскольку глубина может быть достаточно большой (несколько сотен), я советую избегать при обходе графов рекурсивных алгоритмов.
Реальный алгоритм будет чуть сложнее из-за копания ямы и прыжка в нее – получается, что за 4 хода мы перемещаемся на одну клетку вбок и на две вниз (поскольку движение в обратную сторону, то вверх), но легкая модификация алгоритма решает проблему.
Я дополнил картинку цифрами, в том числе с учетом копания ямы и прыжка в нее:

Что нам это напоминает?

Запах золота! И наш бот пойдет на этот запах, как Рокки на сыр (но при этом он не лишается мозгов и уворачивается от монстров, и даже копает им ямы). Давайте составим для него простую жадную стратегию:
- Для каждого золота построим карту расстояний и найдем расстояние до игрока.
- Выберем самое близкое к игроку золото и возьмем его карту для расчета стратегии
- Для каждой клетки карты обозначим через d ее расстояние до золота, тогда стратегическая ценность
Где
Не стоит думать, что наш бот всегда будет бегать к ближайшему золоту. Допустим слева на расстоянии 5 клеток у нас одно золото и далее пустота, а справа два золота на расстоянии 6 и 7. Поскольку реальное золото ценнее воображаемого, бот пойдет вправо.
Прежде чем перейти к более интересным стратегиям, сделаем еще одно улучшение. В игре гравитация тянет игрока вниз, а вверх он может подниматься только по лестницам. А значит, золото, которое находится выше, должно цениться выше. Если высота отчитывается от верхней линии вниз, тогда можно умножить ценность золота (с вертикальной координатой y) на величину
Усложняем стратегии
С одним золотом разобрались, нужно что-то делать со всем золотом, причем не хотелось бы привлекать тяжелую математику. Есть очень элегантное, простое и неправильное (в строгом смысле) решение – если одно золото создает вокруг себя «поле» ценности, то давайте просто сложим все поля ценности от всех клеток с золотом в одну матрицу и используем ее как стратегию. Да, это не оптимальное решение, но несколько единиц золота на средней дистанции могут оказаться ценнее, чем одно близкое.
Однако новое решение порождает новые проблемы – новая матрица ценности может содержать локальные максимумы, вблизи которых золота нет. Потому наш бот может в них попасть и не захочет выходить – значит надо добавить обработчик, проверяющий, что бот оказался в локальном максимуме стратегии и по итогам хода остался на месте. И теперь у нас есть инструмент для борьбы с зависаниями – отменить на N ходов такую стратегию и временно вернуться к стратегии ближайшего золота.
Довольно забавно наблюдать, как застрявший бот меняет стратегию и начинает непрерывно спускаться вниз, съедая все ближайшее золото, на нижних этажах карты бот приходит в себя и пытается вылезти наверх. Этакий доктор Джекил и мистер Хайд.
Стратегия расходится с тактикой
Вот наш бот подходит к золоту под полом:

Оно уже попадает в оптимизирующий алгоритм, осталось сделать 3 шага право, прорубить яму справа и прыгнуть в нее, а далее гравитация сделает все сама. Примерно вот так:

Но бот зависает на месте. Отладка показала, что никакой ошибки нет: бот решил, что оптимальной стратегией является подождать один ход, а потом пройти по указанному маршруту и на последнем анализируемом шаге взять золото. В первом случае он получает выигрыш от полученного золота и выигрыш от воображаемого золота (на последней анализируемой итерации он находится как раз в клетке, где было золото), а во втором – только от настоящего золота (хотя и на ход раньше), а вот выигрыша от стратегии уже нет, потому что место под золотом тухлое и не перспективное. Ну а на следующем ходе он снова решает передохнуть один ход, подобные проблемы мы уже разбирали.
Пришлось модифицировать стратегию – поскольку мы запоминали все золото, которое было съедено на этапе анализа, то из суммарной матрицы стратегической ценности делалось вычитания карт ценности съеденного золота, таким образом, стратегия учитывала достижение тактики (можно было по-другому считать ценность – складывая матрицы только для целого золота, но это вычислительно сложнее, потому что золота на карте намного больше, чем мы можем съесть за 8 ходов).
Но на этом наши мучения не закончились. Допустим, что матрица стратегической ценности имеет локальный максимум и бот подошел к нему на 7 ходов. Будет ли бот идти к нему, чтобы зависнуть? Нет, потому что для любого маршрута, в котором бот за 8 ходов попадет в локальный максимум, выигрыш будет одинаковым. Старая добрая прокрастинация. Причина которой состоит в том, что стратегический выигрыш никак не зависит от момента, в котором мы окажемся в клетке. Первое что приходит в голову – штрафовать бота за простой, но это никак не помогает от бессмысленного хождения влево/вправо. Надо лечить корневую причину – учитывать стратегический выигрыш на каждом ходу (как разницу между стратегической ценностью нового и текущего состояний), уменьшая его со временем на множитель.
Т.е. ввести в выражение для выигрыша дополнительное слагаемое:
значение целевой функции на последнем вообще брать нулевым:
Непроверенная стратегия
Данную стратегию я не проверял на практике, но выглядит многообещающе.
- Поскольку мы знаем все расстояния между точками золота, и расстояния между золотом и игроком, то мы можем найти цепочку игрок-N клеток золота (где N небольшое, например 5 или 6) обладающую наименьшей длинной. Даже простейшим перебором времени хватит.
- Выбрать первое золото в этой цепочки и использовать ее поле ценности как матрицу стратегии.
В этом случае желательно сделать близкой стоимость реального и стоимость воображаемого золота, чтобы бот не кидался в подвал к ближайшему золоту.
Заключительные улучшения
После того, как мы научились «растекаться» по карте, давайте проведем подобное «растекание» от каждого монстра на несколько ходов и найдем все клетки, в которых монстр может оказаться, вместе с числом ходов, за которое он это сделает. Это позволит игроку проползать по трубе над головой монстра совершенно безопасно.
И последний момент – при расчете стратегии и воображаемой ценности золота мы не учитывали положение остальных игроков, просто «стирая» их при анализе карты. Оказывается, что отдельные зависшие оболтусы могут перекрыть собой доступ к целым регионам, потому был добавлен дополнительный обработчик – отслеживать зависающих противников и при анализе замещать их на бетонные блоки.
Особенности реализации
Поскольку основной алгоритм – рекурсивный, то надо уметь быстро изменять объекты состояния и возвращать их исходное для дальнейшей модификации. Я использовал java, язык со сборкой мусора, перебор миллионов изменений, связанных созданием короткоживущих объектов, может вызывать несколько сборок мусора за один ход игры, что может стать фатальным с точки зрения быстродействия. Потому надо быть крайне осторожным в используемых структурах данных, я применял только массивы и списки. Ну или использовать проект Валгала на свой страх и риск :)
Исходный код и игровой сервер
Исходный код можно найти тут на гитхабе. Не судите строго, многое было сделано на скорую руку. Игровой сервер проекта codenjoy обеспечит инфраструктуру для запуска ботов и наблюдения за игрой. На момент создания актуальной была ревизия использовалась ревизия 1.0.26.
Запускать сервер можно следующей строкой:
call mvn -DMAVEN_OPTS=-Xmx1024m -Dmaven.test.skip=true clean jetty:run-war -Dcontext=another-context -Ploderunner
Сам проект крайне любопытный, обеспечивает играми на любой вкус.
Заключение
Если вы все это дочитали до конца без предварительной подготовки и все поняли — то вы редкий молодец.
