Компьютерное зрение занимается поиском и выделением объектов, а обратная задача геофизики заключается в нахождении распределения источников геофизических полей, соответствующего измеренным на поверхности значениям. Что здесь общего и как это могло быть придумано и реализовано задолго до появления первого компьютера? Ведь изложение обсуждаемого метода в публикации 1953 года ссылается на еще более ранние работы 1940-х годов. И что получится, если реализовать программно алгоритмы, придуманные для ручного выполнения (sic!)?

Методы решения обратной задачи геофизики
Данные гравиметрии, или гравиразведки, или просто гравика — представляют собой измерения поля силы тяжести на поверхности Земли. Задача вычисления соответствующих этому полю гравитационных потенциалов, то есть построение объемной модели плотности геологической среду, называется обратной задачей геофизики. Поскольку для всех потенциальных полей решение идентично, далее мы будем говорить только о обратной задаче гравики, подразумевая, что это же применимо к магниторазведке (магнитке) и электроразведке.
С появлением компьютеров, в геофизике придумано множество численных методов решения обратных задач, при этом, все или почти все они опираются на априори заданную конфигурацию нарушений непрерывности (разломов) и данные плотности (по пробуренным скважинам, к примеру) — что делает их непригодными для использования на произвольной территории, а также, исключает возможность их валидации геологическими данными, поскольку все эти данные участвуют в построении модели. На заре появления вычислительных машин это было оправдано, но нужно ли это сегодня? Тем не менее, такой подход стал стандартом.
Мы же хотим найти метод решения такой, что он работает быстро, устойчив к ошибкам исходных данных и универсален. Нужно ли что-то изобретать или, быть может, достаточно обратиться к хорошо забытым старым методам, созданным на заре становления электронных вычислительных машин и даже ранее? Давайте попробуем.
Удивительно, но геологи умели решать обратные задачи задолго по появления электронных вычислительных устройств! Вот, например, решение и прямой и обратной задачи с помощью палетки Гамбурцева (1930е годы или раньше):

Рис. 1. Г.А.Лобова. Полевая геофизика. Гравиразведка — Палетка Гамбурцева
Этот же метод легко может быть реализован численно, итеративным решением прямой задачи, последовательно оптимизируя конфигурацию источников и уменьшая шаг вычислений для получения решения заданной точности. Однако у такого подхода есть серьезный недостаток — метод не устойчив к ошибкам измерения и выбору сетки (хотя, при современных вычислительных ресурсах, можно вычислить множество вариантов на разных сетках и проанализировать сходимость результатов — порой так можно "спасти" даже вычислительно неустойчивые методы).
В поисках лучшего подхода обратимся к широко известной в узких кругах статье Saxov, S. & Nygaard, K. RESIDUAL ANOMALIES AND DEPTH ESTIMATION. GEOPHYSICS 18, 913–928 (1953), которая пару лет назад стала доступна на Sci-Hub. Статья эта является компиляцией лучших рецептов 1940-х для обработки данных гравиметрии — разумеется, без использования компьютеров, так что для упрощения вычислений используются разные трюки (к примеру, круги заменяются квадратами). Приведу выдержку с аннотацией статьи — буквально несколько строк:

Рис. 2. Аннотация статьи Saxov, S. & Nygaard, K. RESIDUAL ANOMALIES AND DEPTH ESTIMATION. GEOPHYSICS 18, 913–928 (1953)
О чем же здесь идет речь? Остаточная гравитационная аномалия (residual gravity anomaly) это аномальное значение (т.е. экстремальное значение — максимальное или минимальное) указанной функции от остаточной гравики (residual gravity), представляющей собой результат низкочастотной фильтрации с граничной длиной волны в первые десятки километров (чтобы быть точным — произведено вычитание региональной составляющей после внесения поправки Буге) данных гравиметрии. Зачем сделана такая оговорка? Тут придется сделать небольшое отступление с пояснением. Дело в том, что гравиметрические измерения использовались для поиска геологических аномалий и изучения геологического строения Земли, но для этого необходимо сначала выделить аномалии соответствующих масштабов — а сделать это для двумерных данных без вычислительных машин очень непросто. Поэтому были придуманы так называемые поправки, результат вычисления которых худо-бедно соответствовал низкочастотной, среднечастотной и высокочастотной фильтрации — редукции Буге, вычитание региональной составляющей и вычисление аномалий в свободном воздухе. Именно эти результаты и публиковались. Поскольку точность первых гравиметрических измерений была не высокой, проводились они по линии (то есть были одномерными) и с шагом в десятки километров, такой способ отлично работал, избавляя от необходимости проводить сложные вычисления каждый раз при работе с данными. Посмотрим на график из Bouguer and Free-Air Gravity Anomalies in terms of spatial spectrum:

Рис. 3. Пространственный спектр аномалий Буге и аномалий в свободном воздухе
К счастью, сегодня нам достаточно использовать двумерный фильтр Гаусса. Впрочем, все еще практически невозможно найти исходные (измеренные) значения гравиметрии — публикуются уже подготовленные данные с поправкой Буге и данные аномалий в свободном воздухе, так что мы вынуждены брать первые, если нужна низкочастотная фильтрация, и вторые, когда требуется высокочастотная фильтрация. Как я уже показывал в публикации Общедоступные данные дистанционного зондирования Земли: как получить и использовать, двумерные пространственные компоненты рельефа с точностью до коэффициента равны пространственным компонентам гравики, значит, это же справедливо и в случае применения достаточно узкого полосового фильтра. Поэтому мы можем использовать в качестве входных данных измеренные значения гравики, значения аномалий в свободном воздухе или рельеф (при этом опираясь на коррелограмму рельефа и гравики для выбора полосы частот фильтра).
Чтобы не усложнять наше исследование, обратим внимание, что низкочастотная фильтрация оказывает влияние на масштабах в десятки километров и более, а примеры из обсуждаемой статьи имеют масштаб порядка километра, так что фильтрацию можно вовсе не учитывать.
Остаточная гравитационная аномалия формулой определена как отношение разности кольцевых средних значений к разности радиусов колец. Как сказано текстом под формулой, когда указанное отношение имеет экстремум, то глубина источника потенциала равна сумме радиусов колец.
Теперь переведем все вышесказанное на современный язык. Формула с картинки оперирует средними значениями по концентрическим кольцам, которые в математике известны как результат кольцевого преобразования Радона, в технологиях компьютерного зрения как кольцевое преобразование Хафа, а в геологии — как фокальное среднее. Такое изобилие наименований из множества разных наук уже как бы намекает, насколько важным и известным является указанное преобразование. Каждая точка исходных данных в результате преобразования получает дополнительную координату — радиус, и как показано в статье, эта дополнительная координата может быть линейно пересчитана в значение глубины. Двумерные значения поля на поверхности (x,y) превратятся в трехмерный куб (x,y,z). Разность последовательных колец, соответственно, равна радиальному градиенту кольцевого преобразования Радона (Хафа). Утверждается, что экстремум радиальной производной кольцевого преобразования Радона (Хафа) по низкочастотной компоненте гравики достигается при значении радиуса преобразования, равном половине глубины источника. Проиллюстрируем это численной моделью поля силы тяжести от однородной сферы, расположенной на глубине H=120м от поверхности (пока смотрим только верхние графики):

Рис. 4. Модель поля силы тяжести для однородной сферы
В самом деле, при радиусе, равном половине глубины, на графике выше присутствует экстремум радиальной производной гравики.
Обратим внимание, здесь мы не использовали кольцевое преобразование Радона (Хафа), поскольку наша модель (гауссиана) обладает кольцевой симметрией и значение в точке для любого радиуса в точности равняется среднему значению по кольцу такого радиуса. А вот в случае обработки реально измеренных данных это очень важный момент, поскольку этот способ устойчив к шумам исходных данных и ошибкам измерения, об этом и сказано в последней строке аннотации к статье. Действительно, ошибка вычисления среднего обратно пропорциональна квадратному корню из числа измерений, которое равно в нашем случае количеству пикселов в кольце и пропорционально радиусу. Нетрудно показать, как это работает в случае идеальных и зашумленных исходных данных, детально это рассмотрено в Robust Depth Estimation Using Circular Mean Radon Transform for the Inverse Potential Problem, 2018, здесь же ограничимся только результатами. На рисунках ниже графически представлены два решения обратной задачи — с использованием центральной точки (красная линия на графиках) и с помощью кольцевого преобразования (синяя линия), при этом хорошо видно, что второй вариант намного точнее при наличии шума в данных.
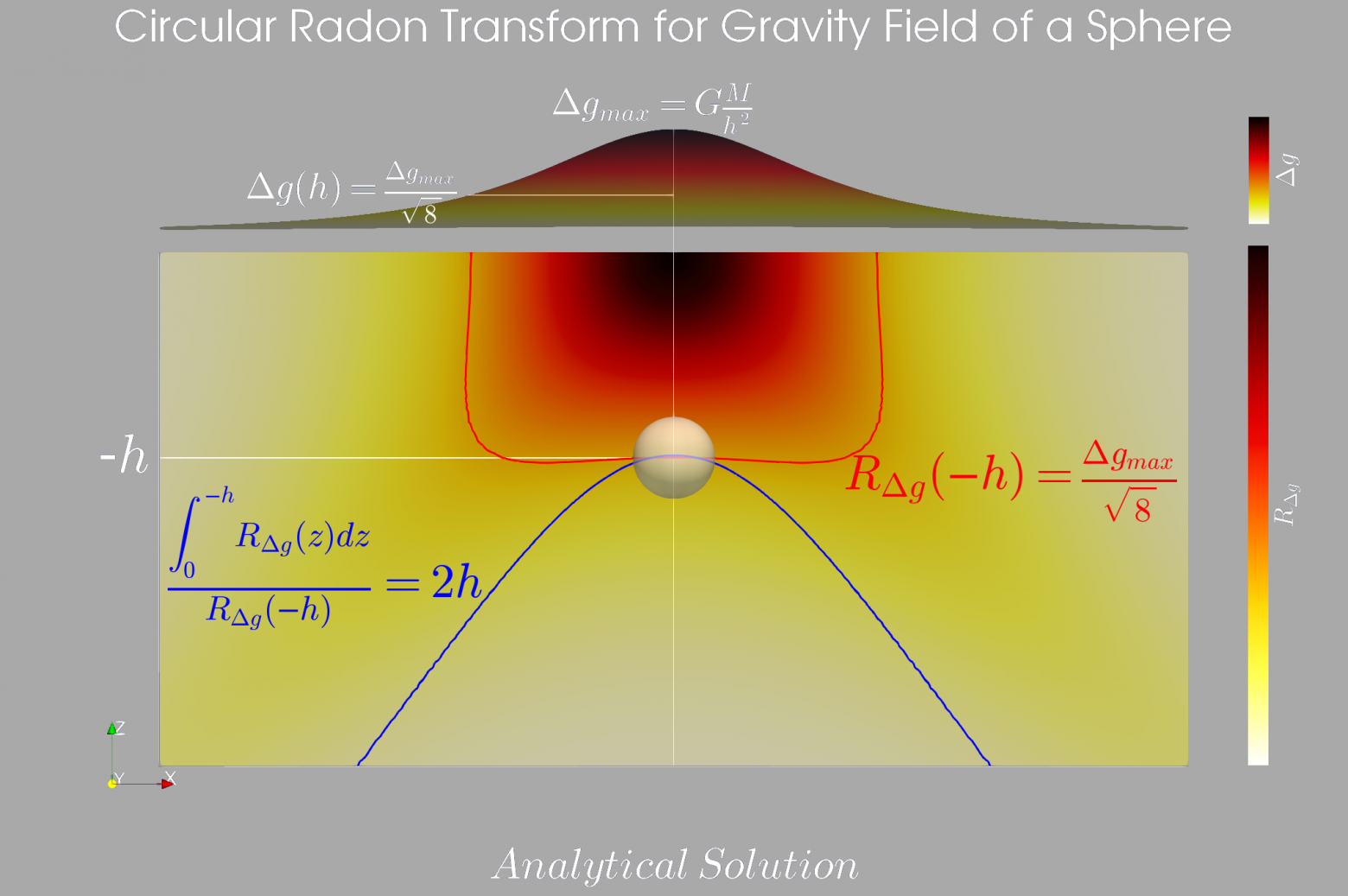
Рис. 5.Решение обратной задачи для однородной сферы с помощью преобразования Радона (Хафа)

Рис. 6. Решение обратной задачи для однородной сферы с помощью преобразования Радона (Хафа) при наличии аддитивного шума
Вернемся к обсуждаемой статье, потому что это еще не все, что в ней можно найти. Действительно, в тексте статьи приведены еще несколько способов решения обратной задачи, притом отношение радиуса к глубине составляет или 2 или √2. С первым мы разобрались, откуда же берется второй коэффициент? Алгоритм вычисления выглядит несколько запутанным, но при этом наводит на мысль о высокочастотной оконной фильтрации из-за трюка с заменой круга на квадрат. Проверим — выполним такую фильтрацию для поля силы тяжести однородной сферы и, в самом деле, значение экстремума сместилось ровно так, как и ожидалось! Смотрите нижние графики на Рис. 4 выше. Есть ли преимущество у такого метода? Да, ведь точно так же и с тем же коэффициентом можно найти центр масс двух сфер, расположенных вертикально, из которых одна имеет избыток плотности, а вторая — недостаток (вертикальный гравитационный диполь). Значит, так можно найти вертикальные изменения плотности (как для вертикального диполя), а горизонтальные будут получены при рассмотрении как центра каждой точки исходных данных (как для отдельных сфер). Это проиллюстрировано с помощью анализа вторых производных, что текстом читать сложно, но легко понятно графически, как показано на рисунках ниже:

Рис. 7. Решение обратной задачи для вертикально расположенной пары однородных сфер с помощью преобразования Радона (Хафа)

Рис. 8. Решение обратной задачи для горизонтально расположенной пары однородных сфер с помощью преобразования Радона (Хафа)
Подробности смотрите в Выделение кольцевых структур в геопотенциальных полях с помощью высокочастотной фильтрации и получение численного решения обратной задачи, 2018.
Подводя итог, мы нашли способ быстро и устойчиво к шумам (ошибкам исходных данных) решать обратную задачу геофизики, для чего требуется выполнить фильтрацию исходных данных и посчитать радиальную производную кольцевого преобразования Радона (Хафа), а потом умножить радиальную координату на масштабный коэффициент глубины 1/√2 для для получения 3D геологической модели. При численном решении на выбранной трехмерной сетке мы получим все границы ячеек, на которых происходит изменение плотности — то есть решение для градиента плотности. Зачастую этого достаточно, хотя есть способы вычислить и сами значения плотности, но это уже другая история. Кроме того, будет полезна IDW (методом обратно взвешенных расстояний) или медианная фильтрация полученной 3D модели для качественной визуализации. Также на практике разумнее использовать полосовую фильтрацию исходных данных для отсечки высокочастотной шумовой компоненты.
Заключение
Мы совершили увлекательный (надеюсь) экскурс в историю геологии и вычислительных методов и нашли много интересного и актуального. И если бы указанная статья попала мне в руки лет на 10 раньше, я бы мог пойти описанным выше путем. Но эта статья до недавнего времени была недоступна онлайн и к методу решения обратной задачи геофизики с помощью кольцевого преобразования Радона, являющегося основой кольцевого преобразования Хафа в технологиях компьютерного зрения, я пришел совсем другим путем, при этом использование кольцевого преобразования Радона позволило чрезвычайно упростить все математические выкладки. Если интересны подробности, смотрите мои статьи по ссылкам в тексте.
Стоило ли того потраченное время на изучение истории геологии? Я считаю, что да, однозначно стоило — в те времена идеи были изложены кратко и алгоритмы вычисления приведены в таком виде, что их легко реализовать вручную (и тем более, программно). В современной же геофизике общепринято публиковать статьи без исходного кода, исходных данных и полученных результатов, что в принципе не позволяет их воспроизвести.
На картинке до хабраката показан пример геологической модели глубинного строения дна океана в районе Марианского желоба, построенной представленным методом, еще больше моделей можно найти в моем LinkedIn (ссылка есть в профиле). Для визуализации использована Open Source программа ParaView с расширением к ней N-Cube ParaView plugin for 3D/4D GIS Data Visualization.
