
Пример стандартной реализации на Python оптимизации инвестиционного портфеля по методу Марковица. Есть много реализаций данного метода. В том числе и на Python. Реализовал еще раз (см. ссылка на GitHub).
Источники
Немного теории возьмем из этих источников:
Лучший инвестиционный портфель через симуляцию Монте-Карло в Python
Портфельная теория Марковица (Википедиа)
Загрузка данных по котировкам
Используем данные с сервиса Yahoo.Finance
! pip install yfinance import yfinance as yf
Берем несколько акций американского рынка за последние 3 месяца.
data = yf.download(['AAPL','GE','BAC','AMD','PLUG','F'],period='3mo')
Курсы закрытия
В расчетах будем использовать дневные курсы закрытия
closeData = data.Close closeData
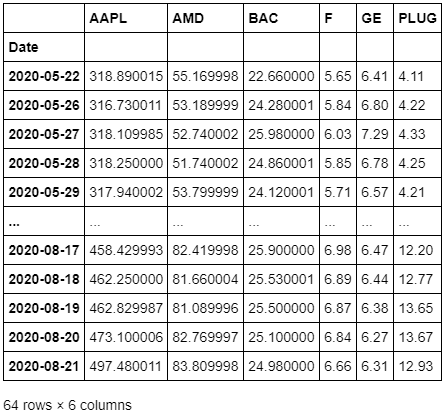
Графики курсов
import matplotlib.pyplot as plt for name in closeData.columns: closeData[name].plot() plt.grid() plt.title(name) plt.show()
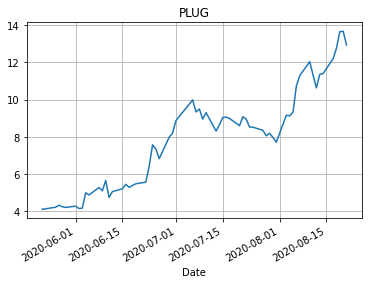
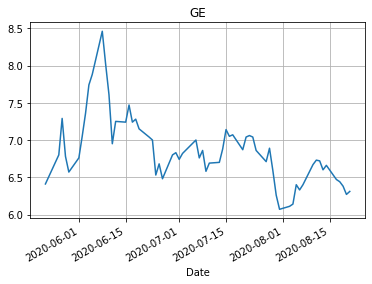
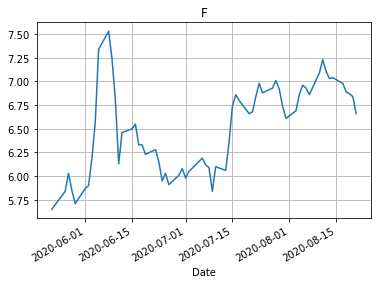

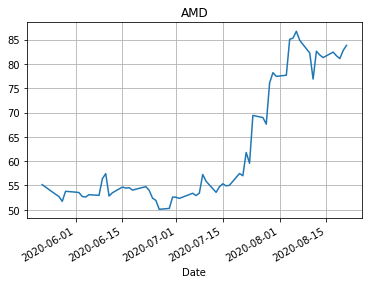

Изменение курсов
Далее понадобятся относительные изменения к предыдущему дню.
dCloseData = closeData.pct_change() dCloseData

Графики относительных изменений курсов
for name in dCloseData.columns: dCloseData[name].plot() plt.title(name) plt.grid() plt.show()
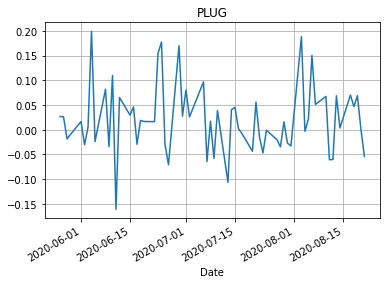
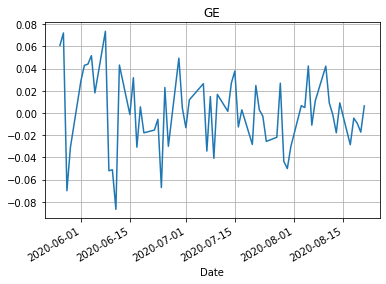
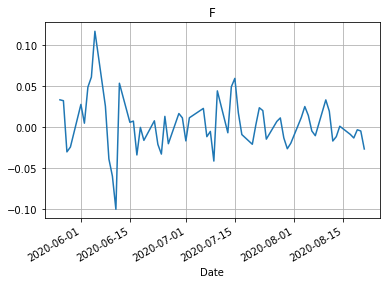
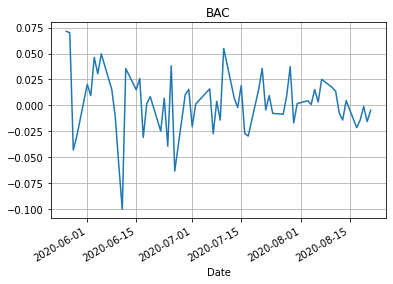

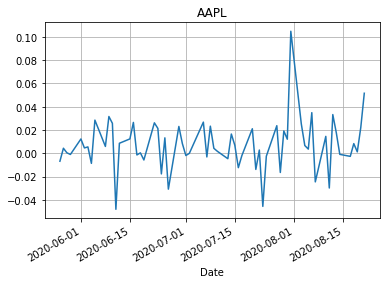
Средняя доходность
Средняя дневная доходность по каждой акции для расчета доходности портфеля.
dohMean = dCloseData.mean() dohMean

Ковариация
Для расчета риска портфеля потребуется ковариационная матрица.
cov = dCloseData.cov() cov

Случайный портфель
Будем генерить случайные портфели. В них сумма долей равна 1 (единице).
import numpy as np cnt = len(dCloseData.columns) def randPortf(): res = np.exp(np.random.randn(cnt)) res = res / res.sum() return res r = randPortf() print(r) print(r.sum())
[0.07519908 0.07594622 0.20932539 0.40973202 0.1234458 0.10635148] 1.0
Доходность портфеля
Доходность портфеля считаем как сумму долей доходностей по каждой акции в портфеле.
def dohPortf(r): return np.matmul(dohMean.values,r) r = randPortf() print(r) d = dohPortf(r) print(d)
[0.0789135 0.13031559 0.25977124 0.21157419 0.13506695 0.18435853] 0.006588795350151513
Риск портфеля¶
Риск портфеля считаем через матричные произведения долей портфеля и матрицы ковариации.
def riskPortf(r): return np.sqrt(np.matmul(np.matmul(r,cov.values),r)) r = randPortf() print(r) rs = riskPortf(r) print(rs)
[0.10999361 0.13739338 0.20412889 0.13648828 0.24021123 0.17178461] 0.02483674110724784
Облако портфелей
Сгенерируем множество портфелей и выведем результат на график риск-доходность. Найдем параметры оптимального портфеля по минимальному риску и по максимальному коэффициенту Шарпа. Сравним с данными усредненного портфеля.
risk = np.zeros(N) doh = np.zeros(N) portf = np.zeros((N,cnt)) for n in range(N): r = randPortf() portf[n,:] = r risk[n] = riskPortf(r) doh[n] = dohPortf(r) plt.figure(figsize=(10,8)) plt.scatter(risk*100,doh*100,c='y',marker='.') plt.xlabel('риск, %') plt.ylabel('доходность, %') plt.title("Облако портфелей") min_risk = np.argmin(risk) plt.scatter([(risk[min_risk])*100],[(doh[min_risk])*100],c='r',marker='*',label='минимальный риск') maxSharpKoef = np.argmax(doh/risk) plt.scatter([risk[maxSharpKoef]*100],[doh[maxSharpKoef]*100],c='g',marker='o',label='максимальный коэф-т Шарпа') r_mean = np.ones(cnt)/cnt risk_mean = riskPortf(r_mean) doh_mean = dohPortf(r_mean) plt.scatter([risk_mean*100],[doh_mean*100],c='b',marker='x',label='усредненный портфель') plt.legend() plt.show()

Выведем данные найденных портфелей.
import pandas as pd print('---------- Минимальный риск ----------') print() print("риск = %1.2f%%" % (float(risk[min_risk])*100.)) print("доходность = %1.2f%%" % (float(doh[min_risk])*100.)) print() print(pd.DataFrame([portf[min_risk]*100],columns=dCloseData.columns,index=['доли, %']).T) print() print('---------- Максимальный коэффициент Шарпа ----------') print() print("риск = %1.2f%%" % (float(risk[maxSharpKoef])*100.)) print("доходность = %1.2f%%" % (float(doh[maxSharpKoef])*100.)) print() print(pd.DataFrame([portf[maxSharpKoef]*100],columns=dCloseData.columns,index=['доли, %']).T) print() print('---------- Средний портфель ----------') print() print("риск = %1.2f%%" % (float(risk_mean)*100.)) print("доходность = %1.2f%%" % (float(doh_mean)*100.)) print() print(pd.DataFrame([r_mean*100],columns=dCloseData.columns,index=['доли, %']).T) print()
---------- Минимальный риск ---------- риск = 1.80% доходность = 0.59% доли, % AAPL 53.890706 AMD 12.793389 BAC 4.117541 F 16.547201 GE 10.945462 PLUG 1.705701 ---------- Максимальный коэффициент Шарпа ---------- риск = 2.17% доходность = 0.88% доли, % AAPL 59.257114 AMD 8.317192 BAC 2.049882 F 8.689935 GE 4.772159 PLUG 16.913719 ---------- Средний портфель ---------- риск = 2.33% доходность = 0.68% доли, % AAPL 16.666667 AMD 16.666667 BAC 16.666667 F 16.666667 GE 16.666667 PLUG 16.666667
Выводы
Повторили классический метод расчета долей инвестиционного портфеля. Получили вполне конкретные результаты.
Оптимизация портфеля по методу Марковица предполагает сохранение параметров в будущем (корреляций между отдельными инструментами и уровня их доходности). Но это не гарантировано. В следующих работах предстоит это проверить.
Понятно, что положительного результата от обозначенной выше проверки ожидать не стоит. Но тогда можно поискать как доработать метод Марковица для получения более гарантированного дохода в будущем. Вот тема для еще одного исследования.
