Эта статья появилась по нескольким причинам.
Во-первых, в подавляющем большинстве книг, интернет-ресурсов и уроков по Data Science нюансы, изъяны разных типов нормализации данных и их причины либо не рассматриваются вообще, либо упоминаются лишь мельком и без раскрытия сути.
Во-вторых, имеет место «слепое» использование, например, стандартизации для наборов с большим количеством признаков — “чтобы для всех одинаково”. Особенно у новичков (сам был таким же). На первый взгляд ничего страшного. Но при детальном рассмотрении может выясниться, что какие-то признаки были неосознанно поставлены в привилегированное положение и стали влиять на результат значительно сильнее, чем должны.
И, в-третьих, мне всегда хотелось получить универсальный метод учитывающий проблемные места.
Повторение — мать учения
Нормализация — это преобразование данных к неким безразмерным единицам. Иногда — в рамках заданного диапазона, например, [0..1] или [-1..1]. Иногда — с какими-то заданным свойством, как, например, стандартным отклонением равным 1.
Ключевая цель нормализации — приведение различных данных в самых разных единицах измерения и диапазонах значений к единому виду, который позволит сравнивать их между собой или использовать для расчёта схожести объектов. На практике это необходимо, например, для кластеризации и в некоторых алгоритмах машинного обучения.
Аналитически любая нормализация сводится к формуле
где — текущее значение,
— величина смещения значений,
— величина интервала, который будет преобразован к “единице”
По сути всё сводится к тому, что исходный набор значений сперва смещается, а потом масштабируется.
На примерах:
Минимакс (MinMax). Цель — преобразовать исходный набор в диапазон [0..1]. Для него:
=
, минимальное значение исходных данных.
=
—
, т.е. за “единичный” интервал берется исходный диапазон значений.
Стандартизация. Цель — преобразовать исходный набор в новый со средним значением равным 0 и стандартным отклонением равным 1.
=
, среднее значение исходных данных.
— равен стандартному отклонению исходного набора.
Для других методов всё аналогично, но со своими особенностями.
В большинстве методов кластеризации или, например, классификации методом ближайших соседей необходимо рассчитывать меру “близости” между различными объектами. Чаще всего в этой роли выступают различные вариации евклидового расстояния.
Представим, что у Вас есть какой-то набор данных с несколькими признаками. Признаки отличаются и по типу распределения, и по диапазону. Чтобы можно было с ними работать, сравнивать, их нужно нормализовать. Причём так, чтобы ни у какого из них не было преимуществ перед другими. По крайней мере, по умолчанию — любые такие предпочтения Вы должны задавать сами и осознанно. Не должно быть ситуации, когда алгоритм втайне от Вас сделал, например, цвет глаз менее важным, чем размер ушей*
* нужно сделать небольшое примечание — здесь речь идёт не о важности признака для, например, результата классификации (это определяется на основе самих данных при обучении модели), а о том, чтобы до начала обучения все признаки были равны по своему возможному влиянию.
Итого, главное условие правильной нормализации — все признаки должны быть равны в возможностях своего влияния.
Шаг 1 — определяем смещение
Чаще всего данные центрируют — т.е. определяют, значение, которое станет новым 0 и “сдвигают” данные относительно него.
Что лучше взять за центр? Некоего «типичного представителя» Ваших данных. Так при использовании стандартизации используется среднее арифметическое значение.
Здесь проявляется проблема № 1 — различные типы распределений не позволяют применять к ним методы, созданные для нормального распределения.
Если Вы спросите любого специалиста по статистике, какое значение лучше всего показывает “типичного представителя” совокупности, то он скажет, что это — медиана, а не среднее арифметическое. Последнее хорошо работает только в случае нормального распределения и совпадает с медианой (алгоритм стандартизации вообще оптимален именно для нормального распределения). А у Вас распределения разных признаков могут (и скорее всего будут) кардинально разные.
Вот, например, различия между медианой и средним арифметическим значением для экспоненциального распределения.
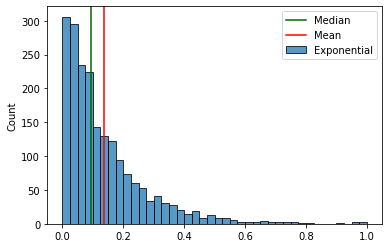
А вот так выглядят эти различия при добавлении выброса:
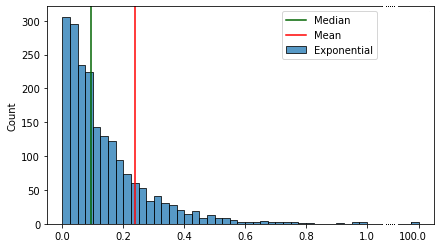
В отличии от среднего значения медиана практически не чувствительна к выбросам и асимметрии распределения. Поэтому её оптимально использовать как “нулевое” значение при центрировании.
В случае, когда нужно не центрировать, а вписать в заданный диапазон, смещением является минимальное значение данных. К этому вернёмся чуть позже.
Шаг 2 — масштабируем
Мы определили нужные величины смещения для всех признаков. Теперь нужно сделать признаки сравнимыми между собой.
Степень возможного влияния признаков определяется величиной их диапазонов после масштабирования. Если оба признака распределены в одинаковых интервалах, например, [-1..1], то и влиять они могут одинаково. Если же изначально один из признаков лежит в диапазоне [-1..1], а второй — в [-1..100], то очевидно, что изменения второго могут оказывать существенно большее влияние. А значит он будет в привилегированном положении по сравнению с первым.
Стандартное отклонение
Вернёмся к примеру стандартизации. В её случае новый диапазон определяется величиной стандартного отклонения. Чем оно меньше, тем диапазон станет “шире”.
Посмотрим на гипотетические распределения различных признаков с одинаковыми начальными диапазонами (так будет нагляднее):

Для второго признака (бимодальное распределение) стандартное отклонение будет больше, чем у первого.
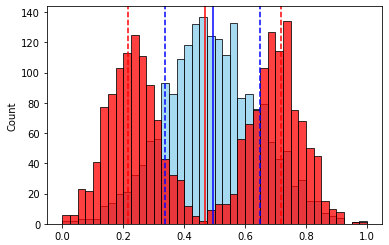
А это значит, что у второго признака новый диапазон после масштабирования (стандартизации) будет “уже”, и его влияние будет меньше по сравнению с первым.

Итог — стандартное отклонение не удовлетворяет начальным требованиям по одинаковому влиянию признаков (величине интервала). Даже не говоря о том, что и наличие выбросов может исказить “истинную” величину стандартного отклонения.
Межквартильный интервал
Другим часто используемым кандидатом является разница между 75-м и 25-м процентилями данных — межквартильный интервал. Т.е. интервал, в котором находятся “центральные” 50% данных набора. Эта величина уже устойчива к выбросам и не зависит от “нормальности” распределения наличия/отсутствия асимметрии.
Но и у неё есть свой серьезный недостаток — если у распределения признака есть значимый “хвост”, то после нормализации с использованием межквартильного интервала он добавит “значимости” этому признаку в сравнении с остальными.
Проблема № 2 — большие “хвосты” распределений признаков.
Пример — два признака с нормальным и экспоненциальным распределениями. Интервалы значений одинаковы
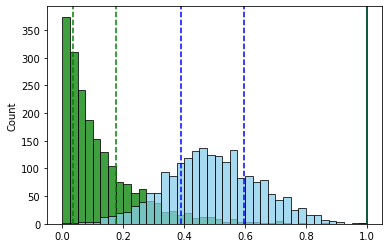
После нормализации с использованием межквартильного интервала (для наглядности оба интервала смещены к минимальным значениям равным нулю).

В итоге интервал у признака с экспоненциальным распределением из-за большого “хвоста” стал больше. А, следовательно, и сам признак стал “влиятельнее”.
Размах значений
Очевидным решением проблемы межквартильного интервала выглядит просто взять размах значений признака. Т.е. разницу между максимальным и минимальным значениями. В этом случае все новые диапазоны будут одинаковыми — равными 1.
И здесь максимально проявляется, наверное, самая частая проблема в подготовке данных, проблема № 3 — выбросы. Присутствие одного или нескольких аномальных (существенно удалённых) значений за пределами диапазона основных элементов набора может ощутимо повлиять на его среднее арифметическое значение и фиктивно увеличить его размах.
Это, пожалуй, самый наглядный пример из всех. К уже использовавшемуся выше набору из 2-х признаков добавим немного выбросов для одного признака
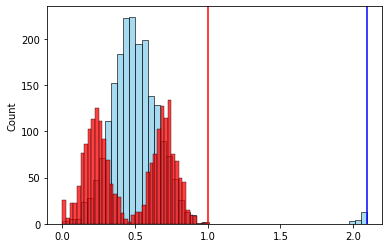
После нормализации по размаху
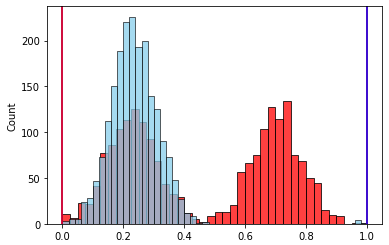
Наличие выброса, который вдвое увеличил размах признака, привело к такому же уменьшению значимого интервала его значений после нормализации. Следовательно влияние этого признака уменьшилось.
Работаем с выбросами
Решением проблемы влияния выбросов при использовании размаха является его замена на интервал, в котором будут располагаться “не-выбросы”. И дальше — масштабировать по этому интервалу.
Искать и удалять выбросы вручную — неблагодарное дело, особенно когда количество признаков ощутимо велико. А иногда выбросы и вовсе нельзя удалять, поскольку это приведёт к потере информации об исследуемых объектах. Вдруг, это не ошибка в данных, а некое аномальное явление, которое нужно зафиксировать на будущее, а не отбрасывать без изучения? Такая ситуация может возникнуть при кластеризации.
Пожалуй, самым массово применяемым методом автоматического определения выбросов является межквартильный метод. Его суть заключается в том, что выбросами “назначаются” данные, которые более чем в 1,5 межквартильных диапазонах (IQR) ниже первого квартиля или выше третьего квартиля.*
* — в некоторых случаях (очень большие выборки и др.) вместо 1,5 используют значение 3 — для определения только экстремальных выбросов.
Схематично метод изображен на рисунке снизу.
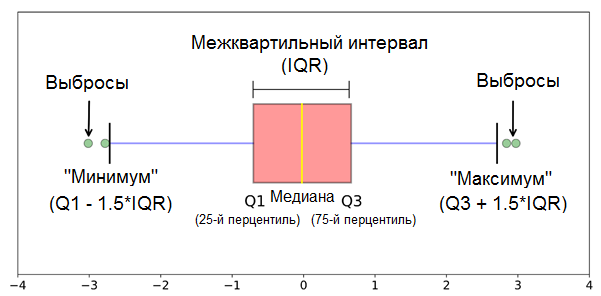
Вроде бы все отлично — наконец-то есть инструмент, и можно приступать к работе.
Но и здесь есть своя ложка дёгтя. В случае наличия длинных хвостов (как, например, при экспоненциальном распределении) слишком много данных попадают в такие “выбросы” — иногда достигая значений более 7%. Избирательное использование других коэффициентов (3 * IQR) опять приводит к необходимости ручного вмешательства — не для каждого признака есть такая необходимость. Их потребуется по отдельности изучать и подбирать коэффициенты. Т.е. универсальный инструмент опять не получается.
Ещё одной существенной проблемой является то, что этот метод симметричный. Полученный “интервал доверия” (1,5 * IQR) одинаков как для малых, так и для больших значений признака. Если распределение не симметричное, то многие аномалии-выбросы с “короткой” стороны просто будут скрыты этим интервалом.
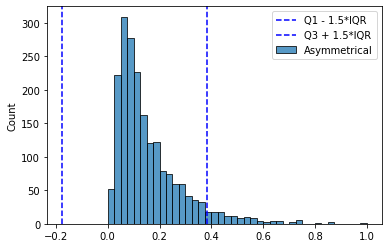
Скорректированный интервал
Красивое решение этих проблем предложили Миа Хаберт и Елена Вандервирен (Mia Hubert and Ellen Vandervieren) в 2007 г. в статье “An Adjusted Boxplot for Skewed Distributions”.
Их идея заключается в вычислении границ “интервал доверия” с учетом асимметрии распределения, но чтобы для симметричного случая он был равен всё тому же 1,5 * IQR.
Для определения некоего “коэффициента асимметрии” они использовали функцию medcouple (MC), которая определяется так:
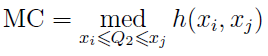
где
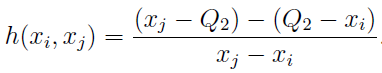
Поиск подходящей формулы для определения границ “интервала доверия” производился с целью сделать долю, приходящуюся на выбросы, не превышающей такую же, как у нормального распределения и 1,5 * IQR — приблизительно 0,7%
В конечном итоге они получили такой результат:
Для :

Для :
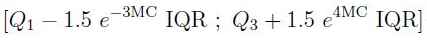
Более подробно про этот метод и его эффективность лучше прочитать в самой статье. Найти ее по названию не составляет труда.
Универсальный инструмент
Теперь, объединяя все найденные плюсы и учитывая проблемы, мы получаем оптимальное решение:
- Центрирование, если оно требуется, производить по медиане.
- Масштабировать набор данных по величине скорректированного интервала.
- (Опционально) — если центрирование не требуется, то смещать масштабированные данные так, чтобы границы скорректированного интервала приходились на [0..1]
Назовем его методом… скорректированного интервала — по названию статьи Mia Hubert и Ellen Vandervieren
Теперь сравним результаты обычных методов с новым. Для примера возьмем уже использовавшиеся выше три распределения с добавлением выбросов.
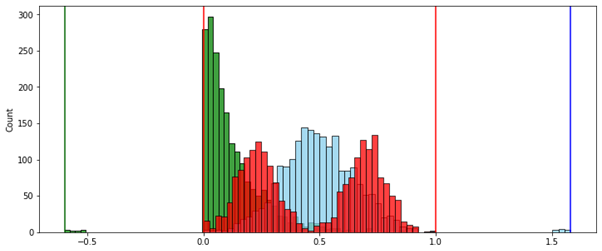
Сравнивать новый инструмент будем с методами стандартизации, робастной нормализации (межквартильный интервал) и минимакса (MinMax — с помощью размаха).
Ситуация № 1 — данные необходимо центрировать. Это используется в кластеризации и многих методах машинного обучения. Особенно, когда необходимо определять меру “близости” объектов.
Стандартизация:
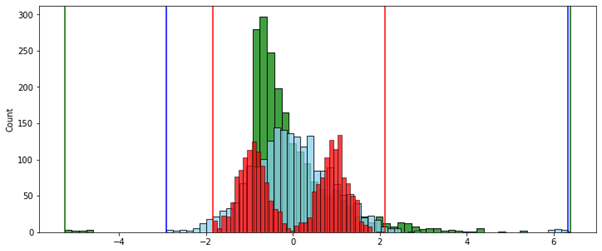
Робастная нормализация (по межквартильному интервалу):

Скорректированный интервал:

Преимущество использования метода скорректированного интервала в том, что каждый из признаков равен по своему возможному влиянию — величина интервала, за пределами которого находятся выбросы, одинакова у каждого из них.
Ситуация № 2 — данные необходимо вписать в заданный интервал. Обычно это [0..1]. Это используется, например, при подготовке данных для входов нейронной сети.
MinMax (по размаху):
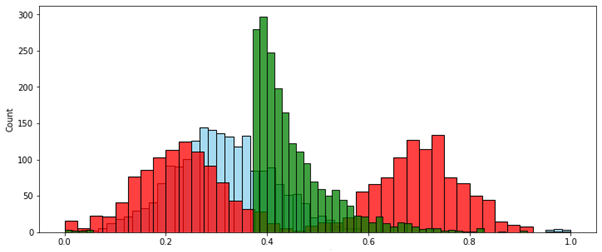
Скорректированный интервал:
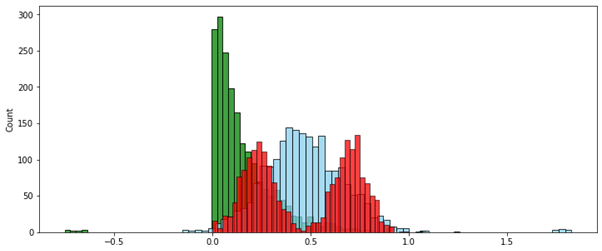
В этом случае метод скорректированного интервала вписал в нужный диапазон только значения без выбросов. Значения-выбросы, выходящие за границы этого диапазона, в зависимости от постановки задачи можно удалить или принудительно приравнять ближайшей границе нужного диапазона — т.е. 0 или 1.
То, что только “нормальные” данные попадают в единичный диапазон [0..1], а выбросы не удаляются, но пропорционально выносятся за его пределы — это крайне полезное свойство, которое сильно поможет при кластеризации объектов со смешанными признаками, как числовыми, так и категорийными. Подробно об этом я напишу в другой статье.
* * *
Напоследок, для возможности пощупать руками этот метод, Вы можете попробовать демонстрационный класс AdjustedScaler из моей библиотеки AdjDataTools.
Он не оптимизирован под работу с очень большим объемом данных и работает только с pandas DataFrame, но для пробы, экспериментов или даже заготовки под что-то более серьезное вполне подойдет. Пробуйте.






