Демонстративно вертим массивы для новичков

Массив — структура, стоявшая у истоков программирования. Но, несмотря на то, что массивам уделяется внимание в каждом курсе уроков по любому языку программирования, от новичков все равно ускользает много важной информации, связанной с логикой взаимодействия с этой структурой.

Цель этого поста — собрать некоторую информацию о массивах, которой когда-то не хватало мне. Пост для новичков.

Что такое массив?

Массив - это структура однотипных данных, расположенная в памяти одним неразрывным блоком.

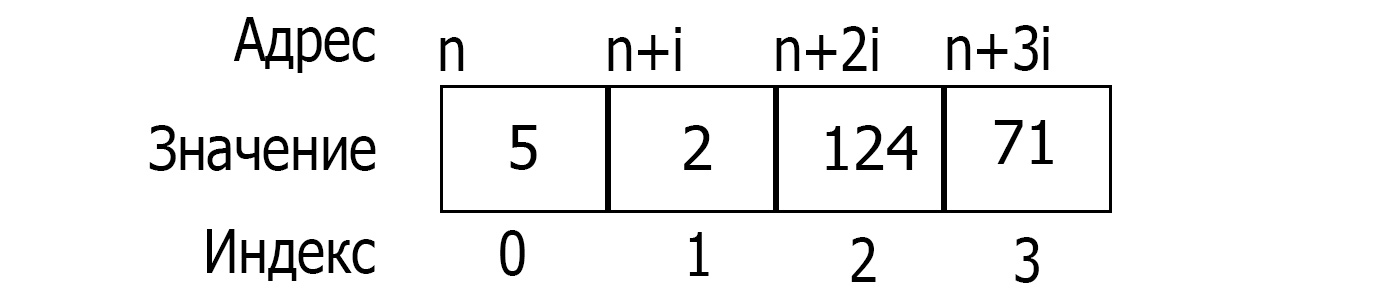
Многомерные массивы хранятся точно также.

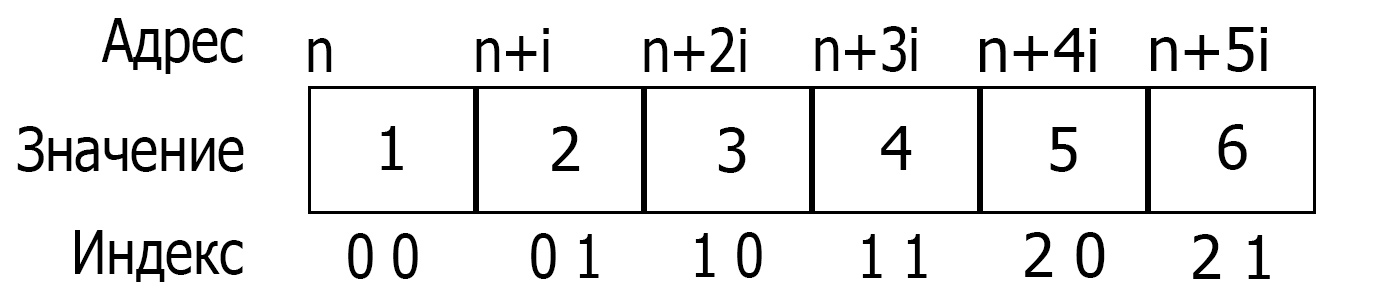
Знание этого позволяет нам по-другому обращаться к элементам массива. Например, у нас есть двухмерный массив из 9 элементов 3х3. Так что есть, как минимум два способа вывести его правильно:

1-й вариант (Самый простой):

int arr[3][3] {1, 2, 3, 4, 5, 6, 7, 8, 9};
int y = 3, x = 3;
for (int i = 0; i < y, ++i) {
	for (int j = 0; j < x; ++j) {
  	std::cout << arr[i][j];
  }
  std::cout << std::endl;
}

2-й вариант (Посложнее):

int arr [9] {1,2,3,4,5,6,7,8,9};
int x = 3, y = 3;
for (int i = 0; i < y; ++i) {
  for (int j = 0; j < x; ++j) {
		std::cout << arr[x * i + j]; // x - ширина массива
    }
  std::cout << std::endl;
}

Формула для обращения к элементу 2-размерного массива, где width - ширина массива, col - нужный нам столбец, а row - нужная нам строчка:

Зная второй вариант, необязательно пользоваться им постоянно, но все же знать стоит. Например, он может быть полезен, когда нужно избавиться от лишних звездочек от указателей на указатели на указатели.

А вот так можно работать с трехмерным массивом

int arr[8] {1,2,3,4,5,6,7,8};
int x = 2, y = 2, z = 2;
for (int i = 0; i < x; ++i) {
	for (int j = 0; j < y; ++j) {
  	for (int k = 0; k < z; ++z) {
    	std::cout << arr[x * y * i + y * j + k];
    }
    std::cout << std::endl;
  }
  std::cout << std::endl;
} 

Этим способом можно обходить трехмерные объекты, например.

Формула доступа к элементам в трехмерном массиве, где height - высота массива, width - ширина массива, depth - глубина элемента(наше новое пространство), col - столбец элемента, а row - строка элемента:

Для получения доступа к элементам массива большей размерности по аналогии в формулу добавляем новые пространства.

Алгоритмы обработки массивов

Я не буду здесь писать про алгоритмы сортировки и алгоритмы поиска, так как найти код для почти любого из этих алгоритмов не составит труда.

Изображения - это целый комплекс из разных заголовков и информации о изображении, и самого изображения хранящемся в виде двухмерного массива.

Обработка изображений хорошо научит работать с двумерными массивами. Вот некоторые алгоритмы, которые пригодились мне для обработки изображений:

1) Зеркальное отражение.

Для того чтобы перевернуть изображение по горизонтали нужно всего лишь читать массив, в котором оно содержится сверху вниз и справа налево.

int data[3][4] = {1,2,3,4,5,6,7,8,9,10,11,12};
int newArray[3][4];
int height = 3, width = 4;
for (int i = 0; i < height; ++i) {
	for (int j = 0; j < width; ++j) {
  	newArray[i][j] = data[i][width - j - 1];
  }
}

По такому же принципу выполняется переворот изображения по вертикали.

int data[3][4] = {1,2,3,4,5,6,7,8,9,10,11,12};
int newArray[3][4];
int height = 3, width = 4;
for (int i = 0; i < height; ++i) {
	for (int j = 0; j < width; ++j) {
  	newArray[i][j] = data[height - i - 1][j];
  }
}

2) Поворот изображения на 90 градусов.

Для поворота изображения нужно повернуть сам двухмерный массив, а чтобы повернуть массив нужно транспонировать двухмерный массив, а затем зеркально отразить по горизонтали.

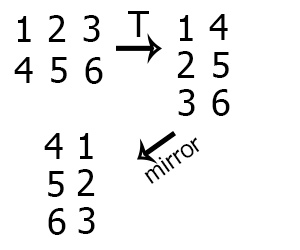
Такой алгоритм появился, когда я нарисовал график координат c точками.

int data[3][2] = {1,2,3,4,5,6};							
int newArray[2][3];					
int height = 3, width = 2; 	// Размеры массива (изображения)
int newHeight = width, newWidth = height;

// Транспонируем матрицу
for (int i = 0; i < newHeight; ++i) {
	for (int j = 0; j < newWidth; ++j) {
  	newArray[i][j] = data[j][i];			// data - массив изображения
  }
}

// Зеркально отражаем по горизонтали матрицу
for (int i = 0; i < newHeight; ++i) {
	for (int j = 0; j < newWidth/2; ++j) {
  	int temp = newArray[i][j];
    newArray[i][j] = newArray[i][newWidth - j - 1];
    newArray[i][newWidth - j - 1] = temp;
  }
}

Хочу обратить ваше внимание, что здесь я применяю другой способ переворота изображения. Вместо выделения памяти под новый массив, здесь просто меняем местами первые и последние элементы.

Примечание: создать массив размерностью высоты и ширины реального изображения на стеке не выйдет. Только на куче с помощью оператора new.

Заключение

Этот небольшой пост не претендует на невероятные открытия мира информатики, но надеюсь успешно поможет немного вникнуть в устройство массивов падаванам мира IT.

Как я сказал в начале, здесь я собрал частичку того, чего не хватало мне при изучении программирования. Как бы эти вещи не казались бесполезными, все студенты университетов, изучающие информационные технологии проходят через это, и не напрасно — это помогает развивать логику и решать более сложные задачи, которые ждут далее. Приведенные выше примеры показывают некоторые важные способы взаимодействия с массивами.

Я надеюсь этот пост будет полезен, и если это будет так, то я напишу продолжение этой темы.