Когда речь заходит о комплексных числах, в первую очередь вспоминают о преобразовании Фурье и прочих аспектах цифровой обработки сигналов. Однако у них есть и более наглядная интерпретация, геометрическая — как точки на плоскости, координатам которой соответствуют действительная и мнимая часть комплексного числа. Рассматривая некоторую кривую как совокупность таких точек, можно описать её как комплексную функцию действительной переменной.
Когда нам нужно начертить окружность в реальной жизни — мы берём циркуль и, уперев его одним (острым) концом, а другим (с грифелем) постепенно вращая, оставляем след на бумаге. В математике это делается аналогично — в роли циркуля выступает мнимая единица
, а в роли вращения — возведение её в степень переменной 
, которую можно интерпретировать как момент времени (а в данном конкретном случае — как угол поворота). Здесь вектор описывает полный круг при изменении значения от 
до 
— что также удобно интерпретировать как четверти на координатной плоскости, когда при изменении целой части одна из проекций на координатную ось меняет свой знак.
Возможно, выражение
кому-то может показаться несколько непривычным, поскольку оно не употребляется в традиционных учебниках математики. В таком случае можно использовать каноническую запись, перейдя к основанию 
: 
.
Также в качестве основания можно использовать минус единицу:
, что часто используется в Wolfram Mathematica для описания единичных комплексных констант.
Разница между функциями
, 
и состоит лишь в периоде для полного оборота вектора по окружности — 
, 
или ; а единицами измерения углов соответственно будут радианы, пол-обороты и кварт-обороты (квадранты). Запись с экспонентой является исторически первой, однако её сложно назвать наглядной — возведение в комплексную степень несколько контринтуитивно. В этой же статье вариант выбран по причине его большей компактности и наглядности.
Эллипс можно начертить растягиванием окружности вдоль одной из осей. Но в таком случае это получится самый обычный параметрический график с участием тригонометрических функций, но без участия комплексных чисел. В комплексных же числах эллипс можно представить как сумму двух векторов разной длины и вращающихся с одной частотой, но в противоположные стороны:
Поскольку в комплексных числах результат суммы тоже не зависит от порядка слагаемых, эту же анимацию можно представить чуть по-другому:
Используя формулу в полярных координатах, можно начертить эллипс одним вектором, но с динамически изменяемой длиной:
Несмотря на то, что фигуры получаются одинаковыми, положение точки (и скорость) в каждый момент времени не совпадают, что хорошо видно на анимации. Поэтому производные этих эллипсов совпадать не будут:
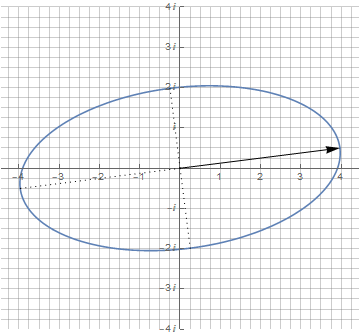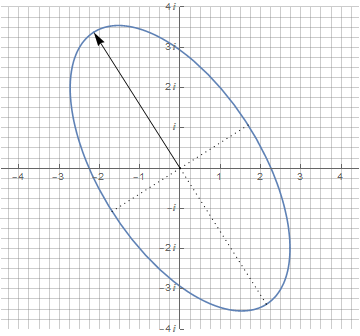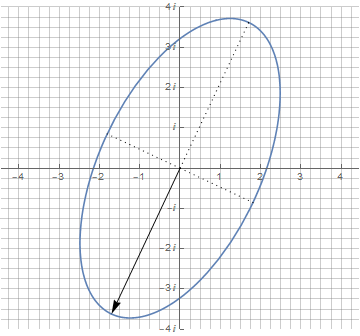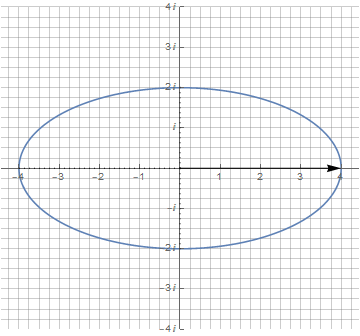
Примечательно, что производная от эллипса, задаваемого суммой двух векторов, осталась тем же эллипсом с теми же пропорциями. Ну а теперь — самое главное преимущество комплексных чисел: чтобы повернуть эллипс на произвольный угол, достаточно просто умножить его на единичный вектор с необходимым углом поворота (phi):
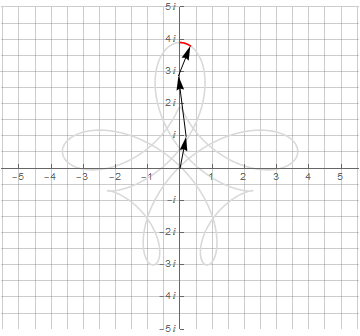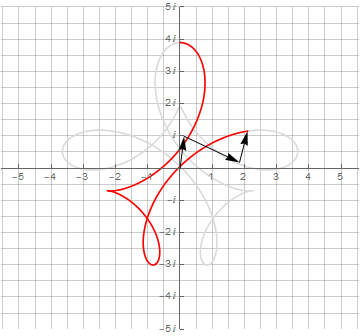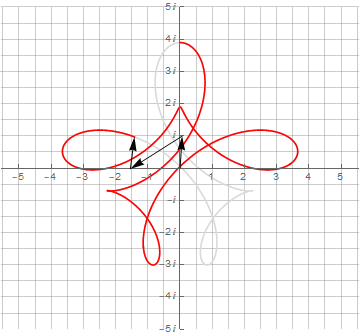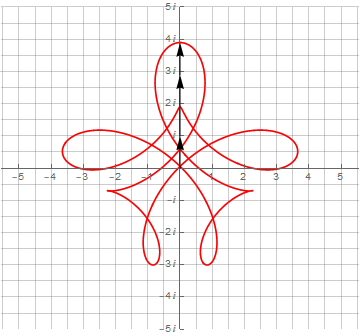
Усложнение получаемых фигур достигается усложнением их мат.модели. Достаточно изменить частоту второго вектора, и можно получить нечто более интересное, а именно — математическую модель спирографа:
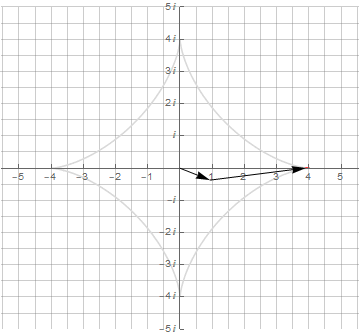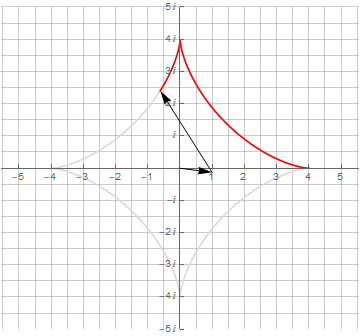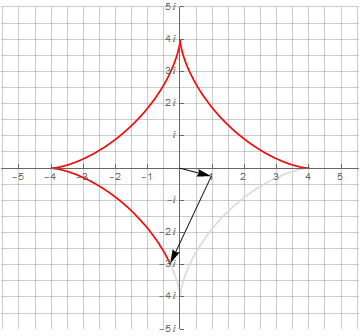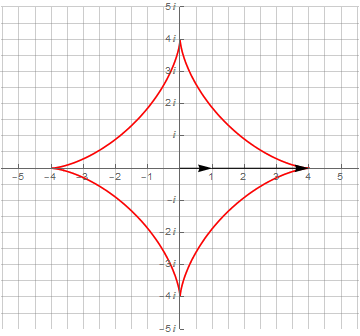
Здесь необходимо обратить внимание на то, что для получения замкнутой кривой одного оборота по окружности оказалось недостаточно — их потребовалось уже 3 и 4 соответственно. Это явилось следствием того, что период второго вектора не укладывается нацело в период первого вектора.
Можно и дальше добавлять векторы и получать всё более и более сложные фигуры:
Давайте немного отвлечёмся от окружностей и начертим синус. Традиционная запись синусоиды выглядит так:
В комплекcном виде формула для синусоды выглядит ненамного сложнее
а график, естественно, выглядит аналогично:
Легко видеть, как была получена это формула — правую часть равенства мы умножили на мнимую единицу, знак равенства заменили на плюс, а
и 
заменили на одну и ту же параметрическую переменную — . Принципиальная разница между этими формулами получилась в том, что теперь можно взять и повернуть синусоиду, просто умножив её на единичный вектор с нужным углом наклона (здесь 45°). Подобные трансформации синусодиды могут потребоваться для того, чтобы направлять её вдоль заданных кривых:
В параметрической форме записи можно модулировать координаты, получая таким образом различные деформации синусоиды, на первый взгляд не имеющих ничего общего с оригиналом:
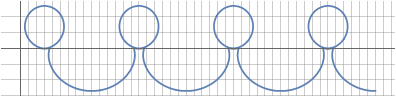
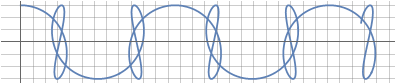
Количество синусоид можно увеличивать, добиваясь эффекта заполнения пространства за счёт равномерного сдвига фаз между ними:
Здесь
— количество синусоид, а 
— порядковый номер синусоиды.
Смещение можно задавать и просто смещением координат — как по одной координате, так и по двум:
Теперь можно попробовать и более сложные варианты — добавить фигурам заполнения. Есть два пути для этого:
1) взять центральную кривую, от которой в обе стороны осциллирует синусоида. Это творческий метод, поскольку внутренняя и внешняя огибающие будут зависеть от множества параметров и могут оказаться весьма неожиданными. Здесь также дополнительной сложностью будет вычисление нормали для синусоидной ленты. Несмотря на то, что её легко вычислить дифференцированием нашей кривой (и умножением на мнимую единицу) с последующей нормировкой функцией
, более интересные варианты получаются заданием её явным образом, в простейшем случае — нормалью к окружности.
2) явно задать внутреннюю и внешние огибающие, а конкретную точку между ними находить интерполяцией всё той же синусоидой. Этот вариант чуть сложнее, зато более предсказуемый.
Начнём с простого:
Обратите внимание: здесь мы не использовали синусоидную ленту — а обошлись лишь одной синусоидой, с некратным периодом 8/5. Для того, чтобы она замкнулась, потребовалось 5 полных оборотов (да, совпадение со знаменателем периода не случайно). Также обратите внимание, что направляющая для синусоиды не перпендикулярна центральной линии — потому что это условие в неё и не закладывалось. А если мы захотим его заложить — то потребуется продифференцировать кривую и повернуть её на 90° умножением на мнимую единицу:
Как видно, получился тоже эллипс, только с другим масштабом (и сдвигом фазы на 90° что в нашем случае значения не имеет). Используя эту функцию (с коррекцией масштаба) в качестве направляющей для синусоидной ленты получим следующую формулу:
Последний штрих — нормировать длину направляющей к единице, чтобы ширина заполняющей ленты была одинаковой (или явно заданной амплитуды). Сделать это можно функцией
или, что то же самое, через деление на абсолютное значение (которое считается как квадратный корень суммы квадратов мнимой и действительной части).
Ну и напоследок — несколько примеров «творческих» орнаментов, полученных просто случайным подбором параметров:
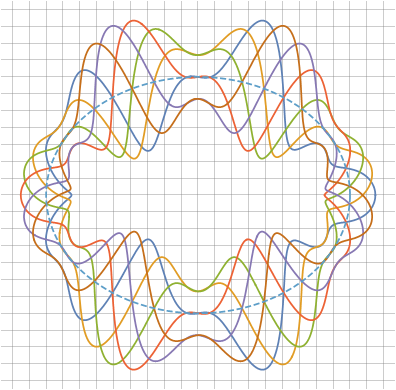
Для второго подхода, интерполяцией между двумя явно заданными огибающими, потребуется вспомогательная функция для изменения масштаба:
в которой при изменении в диапазоне от 
до 
результат функции изменяется соответственно в диапазоне от 
до 
. Во многих системах компьютерной алгебры существуют уже предопределённые функции для этого, и в частности в Wolfram Мathematica ею является функция ![$Rescale\left[x,\left\{x_{\min },x_{\max }\right\},\left\{y_{\min },y_{\max }\right\}\right]$](https://habrastorage.org/getpro/habr/formulas/cea/2d4/03e/cea2d403e18850c7ed875fe95d21e2ac.svg)
. Далее мы будем пользоваться таким же синтаксисом — группируя входные и выходные границы в фигурные скобки, для наглядности.
Итак, если в качестве границ взять эллипс и круг, то получится что-то вроде этого:
Эту формулу можно записать явным образом без использования функции
, подставив аргументы в её определение и упростив:
Однако в таком случае логика работы этой формулы становится намного менее очевидной, и вносить в неё изменения исходя из изначальной логики построения становится намного сложнее.
Поскольку огибающие нам точно известны, то такие фигуры можно комбинировать, использовав одну и ту же огибающую для соседних фигур:
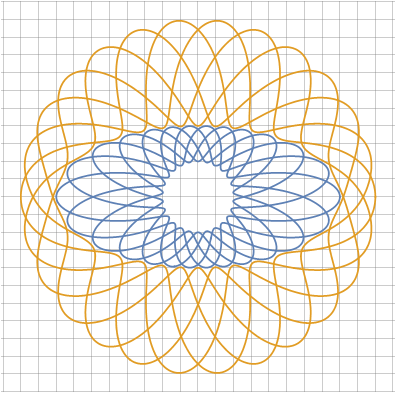
Или чуть сложнее:
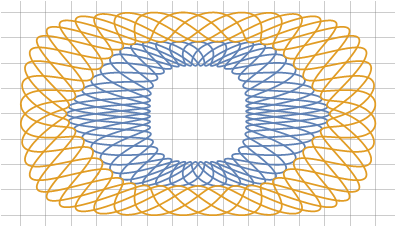
Огибающие, вообще говоря, не обязаны быть гладкими. Используя ранее выведенную формулу, в качестве огибающих можно использовать и многоугольники:
Огибающие можно сделать более выраженными, если синусоиду немного «оквадратить»:
Можно пойти ещё дальше по пути выпрямления и вместо заполнения синусоидой просто использовать прямые отрезки:
Вместо того, чтобы строить синусоидные ленты очевидным способом, их тоже можно получать интерполяцией между двумя прямыми:
Если эту формулу символьно вычислить и упростить, то получим уже известную формулу синусоиды в параметрическом виде:
Запись через функцию позволяет более просто контролировать границы ленты для того, чтобы их можно было собирать как пазл. Например, сделав одну сторону короче другой, можно получить угол в 45° и собрать рамку:
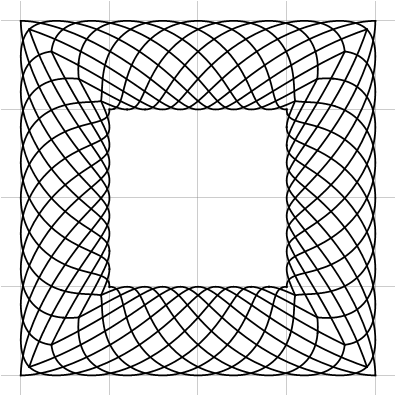
В качестве границ интерполяции можно брать и любые другие кривые:
Можно добавить вариативности и заполнению, модулируя либо координаты границ интерполяции
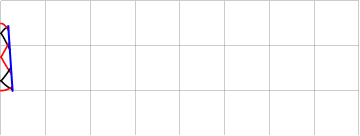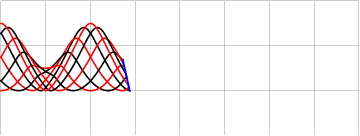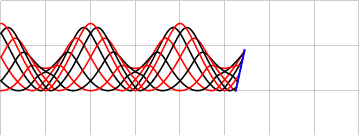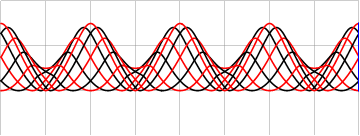
либо частоту заполняющей синусоиды
Здесь были рассмотрены самые простые, базовые техники и фигуры. В качестве дальнейшего развития можно использовать и более сложные математические модели для описания огибающих, в том числе кусочно-непрерывные функции типа кривых Безье, и различные варианты их заполнения. Также комплексные числа можно использовать не только для графики как таковой, но и для описания траекторий различных механизмов типа механизма Чебышёва, что позволит аналитически находить оптимальные параметры и свойства таких механизмов. А если с комплексных чисел перейти на кватернионы — то можно рассматривать подобные построения и в 3Д-пространстве.
Разумеется, подобные задачи можно решать и без комплексных чисел — используя векторы и матричное исчисление, как собственно в основном все и делают. Однако комплексные числа представляются более подходящим инструментом для этого — как минимум более компактным, наглядным и с бОльшим простором для манипуляций, включая интегрирование/дифференцирование, разложение в ряд, преобразование Фурье и прочие инструменты функционального анализа. Впрочем, тема «комплексные числа vs. матрицы» выглядит довольно холиварной — поэтому и продолжить её предлагается уже в комментариях.
P.S. Скачать исходник статьи можно на GitHub.
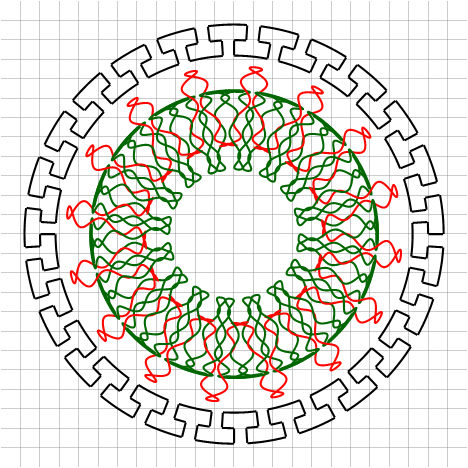
▍ Окружность
Когда нам нужно начертить окружность в реальной жизни — мы берём циркуль и, уперев его одним (острым) концом, а другим (с грифелем) постепенно вращая, оставляем след на бумаге. В математике это делается аналогично — в роли циркуля выступает мнимая единица
, а в роли вращения — возведение её в степень переменной , которую можно интерпретировать как момент времени (а в данном конкретном случае — как угол поворота). Здесь вектор описывает полный круг при изменении значения от до — что также удобно интерпретировать как четверти на координатной плоскости, когда при изменении целой части одна из проекций на координатную ось меняет свой знак.
Возможно, выражение
кому-то может показаться несколько непривычным, поскольку оно не употребляется в традиционных учебниках математики. В таком случае можно использовать каноническую запись, перейдя к основанию : .Также в качестве основания можно использовать минус единицу:
, что часто используется в Wolfram Mathematica для описания единичных комплексных констант.Разница между функциями
, и состоит лишь в периоде для полного оборота вектора по окружности — , или ; а единицами измерения углов соответственно будут радианы, пол-обороты и кварт-обороты (квадранты). Запись с экспонентой является исторически первой, однако её сложно назвать наглядной — возведение в комплексную степень несколько контринтуитивно. В этой же статье вариант выбран по причине его большей компактности и наглядности.▍ Эллипс
Эллипс можно начертить растягиванием окружности вдоль одной из осей. Но в таком случае это получится самый обычный параметрический график с участием тригонометрических функций, но без участия комплексных чисел. В комплексных же числах эллипс можно представить как сумму двух векторов разной длины и вращающихся с одной частотой, но в противоположные стороны:
Поскольку в комплексных числах результат суммы тоже не зависит от порядка слагаемых, эту же анимацию можно представить чуть по-другому:
Используя формулу в полярных координатах, можно начертить эллипс одним вектором, но с динамически изменяемой длиной:
Несмотря на то, что фигуры получаются одинаковыми, положение точки (и скорость) в каждый момент времени не совпадают, что хорошо видно на анимации. Поэтому производные этих эллипсов совпадать не будут:
формулы производных
Примечательно, что производная от эллипса, задаваемого суммой двух векторов, осталась тем же эллипсом с теми же пропорциями. Ну а теперь — самое главное преимущество комплексных чисел: чтобы повернуть эллипс на произвольный угол, достаточно просто умножить его на единичный вектор с необходимым углом поворота (phi):
▍ Гипотрохоида и прочее
Усложнение получаемых фигур достигается усложнением их мат.модели. Достаточно изменить частоту второго вектора, и можно получить нечто более интересное, а именно — математическую модель спирографа:
Здесь необходимо обратить внимание на то, что для получения замкнутой кривой одного оборота по окружности оказалось недостаточно — их потребовалось уже 3 и 4 соответственно. Это явилось следствием того, что период второго вектора не укладывается нацело в период первого вектора.
Можно и дальше добавлять векторы и получать всё более и более сложные фигуры:
▍ Синусы и синусоидные ленты
Давайте немного отвлечёмся от окружностей и начертим синус. Традиционная запись синусоиды выглядит так:
В комплекcном виде формула для синусоды выглядит ненамного сложнее
а график, естественно, выглядит аналогично:
Легко видеть, как была получена это формула — правую часть равенства мы умножили на мнимую единицу, знак равенства заменили на плюс, а
и заменили на одну и ту же параметрическую переменную — . Принципиальная разница между этими формулами получилась в том, что теперь можно взять и повернуть синусоиду, просто умножив её на единичный вектор с нужным углом наклона (здесь 45°). Подобные трансформации синусодиды могут потребоваться для того, чтобы направлять её вдоль заданных кривых:
В параметрической форме записи можно модулировать координаты, получая таким образом различные деформации синусоиды, на первый взгляд не имеющих ничего общего с оригиналом:
Количество синусоид можно увеличивать, добиваясь эффекта заполнения пространства за счёт равномерного сдвига фаз между ними:
Здесь
— количество синусоид, а — порядковый номер синусоиды.Смещение можно задавать и просто смещением координат — как по одной координате, так и по двум:
▍ Розетты
Теперь можно попробовать и более сложные варианты — добавить фигурам заполнения. Есть два пути для этого:
1) взять центральную кривую, от которой в обе стороны осциллирует синусоида. Это творческий метод, поскольку внутренняя и внешняя огибающие будут зависеть от множества параметров и могут оказаться весьма неожиданными. Здесь также дополнительной сложностью будет вычисление нормали для синусоидной ленты. Несмотря на то, что её легко вычислить дифференцированием нашей кривой (и умножением на мнимую единицу) с последующей нормировкой функцией
, более интересные варианты получаются заданием её явным образом, в простейшем случае — нормалью к окружности.2) явно задать внутреннюю и внешние огибающие, а конкретную точку между ними находить интерполяцией всё той же синусоидой. Этот вариант чуть сложнее, зато более предсказуемый.
Начнём с простого:
Обратите внимание: здесь мы не использовали синусоидную ленту — а обошлись лишь одной синусоидой, с некратным периодом 8/5. Для того, чтобы она замкнулась, потребовалось 5 полных оборотов (да, совпадение со знаменателем периода не случайно). Также обратите внимание, что направляющая для синусоиды не перпендикулярна центральной линии — потому что это условие в неё и не закладывалось. А если мы захотим его заложить — то потребуется продифференцировать кривую и повернуть её на 90° умножением на мнимую единицу:
Как видно, получился тоже эллипс, только с другим масштабом (и сдвигом фазы на 90° что в нашем случае значения не имеет). Используя эту функцию (с коррекцией масштаба) в качестве направляющей для синусоидной ленты получим следующую формулу:
Последний штрих — нормировать длину направляющей к единице, чтобы ширина заполняющей ленты была одинаковой (или явно заданной амплитуды). Сделать это можно функцией
или, что то же самое, через деление на абсолютное значение (которое считается как квадратный корень суммы квадратов мнимой и действительной части).
Ну и напоследок — несколько примеров «творческих» орнаментов, полученных просто случайным подбором параметров:
▍ Розетты с интерполяцией
Для второго подхода, интерполяцией между двумя явно заданными огибающими, потребуется вспомогательная функция для изменения масштаба:
в которой при изменении
в диапазоне от до результат функции изменяется соответственно в диапазоне от до . Во многих системах компьютерной алгебры существуют уже предопределённые функции для этого, и в частности в Wolfram Мathematica ею является функция . Далее мы будем пользоваться таким же синтаксисом — группируя входные и выходные границы в фигурные скобки, для наглядности.Итак, если в качестве границ взять эллипс и круг, то получится что-то вроде этого:
![$f(t) = Rescale\left[\cos \left(\frac{13 \pi t}{5}\right),\{-1,1\},\left\{i^t,i^{-t}+3 i^t\right\}\right]$](https://habrastorage.org/getpro/habr/formulas/0d3/1e5/41a/0d31e541a9f5aa17b5dfaa129b783354.svg)
Эту формулу можно записать явным образом без использования функции
, подставив аргументы в её определение и упростив:
Однако в таком случае логика работы этой формулы становится намного менее очевидной, и вносить в неё изменения исходя из изначальной логики построения становится намного сложнее.
Поскольку огибающие нам точно известны, то такие фигуры можно комбинировать, использовав одну и ту же огибающую для соседних фигур:
![$f_1(t) = Rescale\left[\cos \left(\frac{13 \pi t}{5}\right),\{-1,1\},\left\{i^t,8 i^t \sqrt{\frac{2}{20-12 \cos (\pi t)}}\right\}\right]$](https://habrastorage.org/getpro/habr/formulas/623/08c/95a/62308c95a89f9c3985d124e9546f8c89.svg)
![$f_2(t) = Rescale\left[\cos \left(\frac{13 \pi t}{5}\right),\{1,-1\},\left\{3i^t,8 i^t \sqrt{\frac{2}{20-12 \cos (\pi t)}}\right\}\right]$](https://habrastorage.org/getpro/habr/formulas/96e/980/ad8/96e980ad85418dfea24507e57b23e842.svg)
Или чуть сложнее:
![$\small f_1(t) =Rescale\left[\cos \left(\frac{24 \pi t}{5}\right),\{-1,1\},\left\{i^t-\frac{2 i^{5 t}}{35}+\frac{i^{9 t}}{189},2 \left(\frac{3 i^{-5 t}}{70}+\frac{i^{-t}}{4}+i^t+\frac{i^{9 t}}{252}\right)\right\}\right]$](https://habrastorage.org/getpro/habr/formulas/dc8/7bd/646/dc87bd646a3aa33d69bb18ce3d473099.svg)
![$\small f_2(t) =Rescale\left[\cos \left(\frac{24 \pi t}{5}\right),\{-1,1\},\left\{3 \left(-\frac{1}{12} i^{-3 t}+\frac{i^{-t}}{4}+i^t\right),2 \left(\frac{3 i^{-5 t}}{70}+\frac{i^{-t}}{4}+i^t+\frac{i^{9 t}}{252}\right)\right\}\right]$](https://habrastorage.org/getpro/habr/formulas/738/01a/265/73801a265dac89b997ff3f1eb3e05f09.svg)
Огибающие, вообще говоря, не обязаны быть гладкими. Используя ранее выведенную формулу, в качестве огибающих можно использовать и многоугольники:
![$f(t) = Rescale\left[\cos \left(\frac{33 \pi t}{5}\right),\{-1,1\},\left\{2 i^t,\frac{i^t \left(i^{n t}\right)^{1/n}}{1+\left(i^{n t}\right)^{2/n}}\right\}\right],n \to 3$](https://habrastorage.org/getpro/habr/formulas/8ce/e5b/acc/8cee5bacc21a131a8fdb76e9ea27f11c.svg)
Огибающие можно сделать более выраженными, если синусоиду немного «оквадратить»:
![$f(t) = -i \text{Rescale}\left[\sin \left(\frac{1}{2} \pi \sin \left(\frac{31 \pi t}{5}\right)\right),\{-1,1\},\left\{\frac{i^t \left(i^{4 t}\right)^{1/4}}{1+\left(i^{4 t}\right)^{2/4}},\frac{2 \left(i^t \left(i^{5 t}\right)^{1/5}\right)}{1+\left(i^{5 t}\right)^{2/5}}\right\}\right]$](https://habrastorage.org/getpro/habr/formulas/e84/b25/4dc/e84b254dc269babb9c8736c55acd4695.svg)
Можно пойти ещё дальше по пути выпрямления и вместо заполнения синусоидой просто использовать прямые отрезки:
▍ Бордюры
Вместо того, чтобы строить синусоидные ленты очевидным способом, их тоже можно получать интерполяцией между двумя прямыми:
![$f(t) = Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)\right),\{-1,1\},\{t-i,t+i\}\right]$](https://habrastorage.org/getpro/habr/formulas/353/0a4/409/3530a4409eae350d1af7380d5caa22ad.svg)
Если эту формулу символьно вычислить и упростить, то получим уже известную формулу синусоиды в параметрическом виде:
Запись через функцию
позволяет более просто контролировать границы ленты для того, чтобы их можно было собирать как пазл. Например, сделав одну сторону короче другой, можно получить угол в 45° и собрать рамку:![$f(t)=Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)\right),\{-1,1\},\{2 t,t+i\}\right],-1\leq t\leq 1$](https://habrastorage.org/getpro/habr/formulas/8ba/41f/588/8ba41f58885ea266095fcb01006bb19d.svg)
В качестве границ интерполяции можно брать и любые другие кривые:
![$f(t)=Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)\right),\{-1,1\},\left\{t,t+\frac{1}{2} i \cos (\pi t)+i\right\}\right]$](https://habrastorage.org/getpro/habr/formulas/96e/efd/b58/96eefdb58fc5bc5ae1942cb56acfe89f.svg)
![$f(t)=Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)\right),\{-1,1\},\left\{t-\frac{1}{5} \sin (\pi t),t+\frac{1}{2} i \cos (\pi t+\sin (\pi t))+i\right\}\right]$](https://habrastorage.org/getpro/habr/formulas/f2d/40e/cb6/f2d40ecb630f965ed724d9cd816f97d2.svg)
![$f(t)=Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)\right),\{-1,1\},\left\{t-\frac{1}{2} i \cos \left(\frac{\pi t}{3}\right)-i,t+\frac{1}{2} i \cos (\pi t)+i\right\}\right]$](https://habrastorage.org/getpro/habr/formulas/83b/a8b/ce3/83ba8bce3125deaf9918acd239ab47b3.svg)
Можно добавить вариативности и заполнению, модулируя либо координаты границ интерполяции
![$f(t)=Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)\right),\{-1,1\},\left\{t+\frac{1}{5} \sin (\pi t),t+\frac{1}{2} i \cos (\pi t)+i\right\}\right]$](https://habrastorage.org/getpro/habr/formulas/7c8/579/5b9/7c85795b92102142a96a9f7ee00a85c9.svg)
![$f(t) =Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)\right),\{-1,1\},\left\{t-\frac{1}{5} \sin (\pi t),t+\frac{1}{2} i \cos (\pi t)+i\right\}\right]$](https://habrastorage.org/getpro/habr/formulas/3d9/c99/302/3d9c99302e84eae1b93a3207d18af801.svg)
либо частоту заполняющей синусоиды
![$f(t)=Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)+\cos (\pi t)\right),\{-1,1\},\{t,t+i\}\right]$](https://habrastorage.org/getpro/habr/formulas/3dc/07f/ba3/3dc07fba317863647122dc07776f9f01.svg)
![$f(t)=Rescale\left[\cos \left(\pi \left(\frac{j}{n}+t\right)+2 \cos ^3(\pi t)\right),\{-1,1\},\{t,t+i\}\right]$](https://habrastorage.org/getpro/habr/formulas/e6a/a7c/313/e6aa7c313caf14b5c2478e8a4671a074.svg)
▍ Заключение
Здесь были рассмотрены самые простые, базовые техники и фигуры. В качестве дальнейшего развития можно использовать и более сложные математические модели для описания огибающих, в том числе кусочно-непрерывные функции типа кривых Безье, и различные варианты их заполнения. Также комплексные числа можно использовать не только для графики как таковой, но и для описания траекторий различных механизмов типа механизма Чебышёва, что позволит аналитически находить оптимальные параметры и свойства таких механизмов. А если с комплексных чисел перейти на кватернионы — то можно рассматривать подобные построения и в 3Д-пространстве.
Разумеется, подобные задачи можно решать и без комплексных чисел — используя векторы и матричное исчисление, как собственно в основном все и делают. Однако комплексные числа представляются более подходящим инструментом для этого — как минимум более компактным, наглядным и с бОльшим простором для манипуляций, включая интегрирование/дифференцирование, разложение в ряд, преобразование Фурье и прочие инструменты функционального анализа. Впрочем, тема «комплексные числа vs. матрицы» выглядит довольно холиварной — поэтому и продолжить её предлагается уже в комментариях.
P.S. Скачать исходник статьи можно на GitHub.
