Бывает так, что попадается какая-то задача, находится ее решение, причем довольно неплохое, но потом эта задача все равно не отпускает. Появляется навязчивая мысль о том, что у нее должно быть более оптимальное решение. Примерно так и получилось с задачей динамического ценообразования для авиабилетов, которую мы описывали более года назад в прошлой статье. Решение основывалось на алгоритме семплирования Томпсона. Компьютерное моделирование продаж показывало превосходные результаты, а тот факт, что такие гиганты как Walmart и Amazon уже давным давно и более чем успешно используют различные модификации этого алгоритма, только укрепляло уверенность в том, что мы на верном пути и иных способов оптимального решения задачи просто нет. Но в подавляющем большинстве случаев то, что отлично и везде работает, в авиаотрасли должно работать лучше. Не потому что так хочется, а потому что в этом действительно есть сильная потребность. Должно быть меньше экспериментов с ценой, она не должна меняться очень часто, а сам процесс поиска оптимальной цены должен быть еще быстрее. Но самое главное, алгоритм семплирования Томпсона не позволяет получить более-менее адекватную вероятностную модель спроса, без которой невозможно в полной мере использовать стохастическое программирование и заняться задачами глобальной оптимизации.
Распределение спроса вместо кривой спроса
Переосмысление подхода к решению задачи началось, когда один из членов команды обратил внимание на предпринимателей розничной торговли, которые открывают социальные магазины. Это своеобразная форма благотворительности, которая заключается в том, что в магазине нет продавца, вместо которого есть что-то вроде ящика для пожертвований. В таком магазине можно взять любой товар с полки и самостоятельно решить сколько денег за него отдать. Все это конечно любопытно и наталкивает на множество размышлений, но примечательно то, что в подобных магазинах обычная кривая спроса превращается в некоторое распределение.
Что бы продемонстрировать это, а также все дальнейшие примеры мы будем использовать язык Python, поэтому сразу сделаем все необходимые импорты:
У нас нет данных о том сколько денег каждый посетитель подобного магазина платил за какой-то отдельно взятый товар, но это не помешает нам немного поразмышлять в этом направлении. Например, в знаменитом наборе данных tips отражена схожая ситуация, в которой посетителям ресторана нужно было самостоятельно принять решение о размере чаевых. Вряд ли в меню ресторана было большими красными буквами указано требование о том, что размер чаевых должен составлять 20% от стоимости заказа, но если взглянуть на график, то мы увидим, что значительная часть посетителей старается следовать этому негласному правилу:

В какой-то мере это негласное правило можно считать социальной нормой. В любом случае, схожий механизм работает и в социальных магазинах: какая-то часть посетителей руководствуется чувством справедливости и старается платить столько, сколько указано на ценнике товара. В наборе данных tips можно оценить влияние других факторов на размер чаевых: день недели, время суток, пол человека, оплачивающего счет, или количество людей в группе, выполнившей заказ. Очевидно, что каждый посетитель социального магазина, так же может руководствоваться множеством самых разных факторов: уровень дохода и наличие работы, количество человек в семье, торопится он на данный момент или нет, есть кто-нибудь рядом или нет и т.д. По центральной предельной теореме распределение спроса на товар в таких магазинах можно считать предельно нормальным.
Если взять какой-нибудь конкретный товар в магазине без продавца, на ценнике которого указана стоимость в 12 рублей, то распределение спроса на него вполне могло бы выглядеть так:

На самом деле мы можем лишь гадать как в действительности мог бы выглядеть этот график, так как у нас нет реальных данных. Но эти размышления наталкивают на мысль о том, что у спроса действительно должно быть какое-то распределение и, скорее всего, оно должно быть нормальным. В тоже самое время, если это действительно так, то это неизбежно должно приводить к тому, что какая-то часть распределения может оказаться в области отрицательных цен. Например, если бы мы опросили всех потенциальных покупателей некоторого города «A» о том, сколько они готовы заплатить за авиабилеты в город «B», ничего им не сообщая о его истинной стоимости, то вполне могли бы получить следующий результат:

С одной стороны, принятие во внимание отрицательных цен выглядит нелогичным и даже комичным. С другой стороны, вряд ли какая-то значительная часть читателей согласится слетать на выходные в Афганистан, даже если авиакомпания предложит за перелет приличную сумму денег. Так и во многих сферах коммерческой деятельности возможны ситуации, когда компании выгодно продавать свой товар или услуги по отрицательным ценам, чем не продавать вовсе. К примеру товар, который имеет ограниченный срок годности, после которого он должен быть утилизирован (бытовая химия, косметика, продукты питания) – компании проще отдать бесплатно или немного доплатить покупателям, чем оплачивать стоимость транспортировки и утилизации в дальнейшем. Попытка сэкономить и не утилизировать товар может привести к увеличению общих затрат компании, т.к. бесконечно хранить у себя на складах такие товары не получится. Это увеличивает стоимость логистик (складской), да и ресурсы складов не бесконечны. О примере продажи товаров с отрицательной ценой каждый слышал: цена нефти Brent опустилась ниже 0 в 2020 году. Но вернемся к распределению спроса: вовсе не обязательно, что какая-то часть спроса должна находиться в области отрицательных цен, но это действительно возможно, хотя бы потому что всегда могут найтись люди, которым определенный товар будет не нужен даже за значительную доплату.
Если спрос распределен нормально, то мы можем легко получить кривую спроса, для чего нужно просто начать продавать товар. Да, при более точном рассмотрении, обладая большим набором данных, мы можем прийти к тому, что спрос имеет другое распределение, но в первом приближении большинство методологий рекомендует начинать с нормального распределения, а дальше уже уточнять более сложными распределениями.
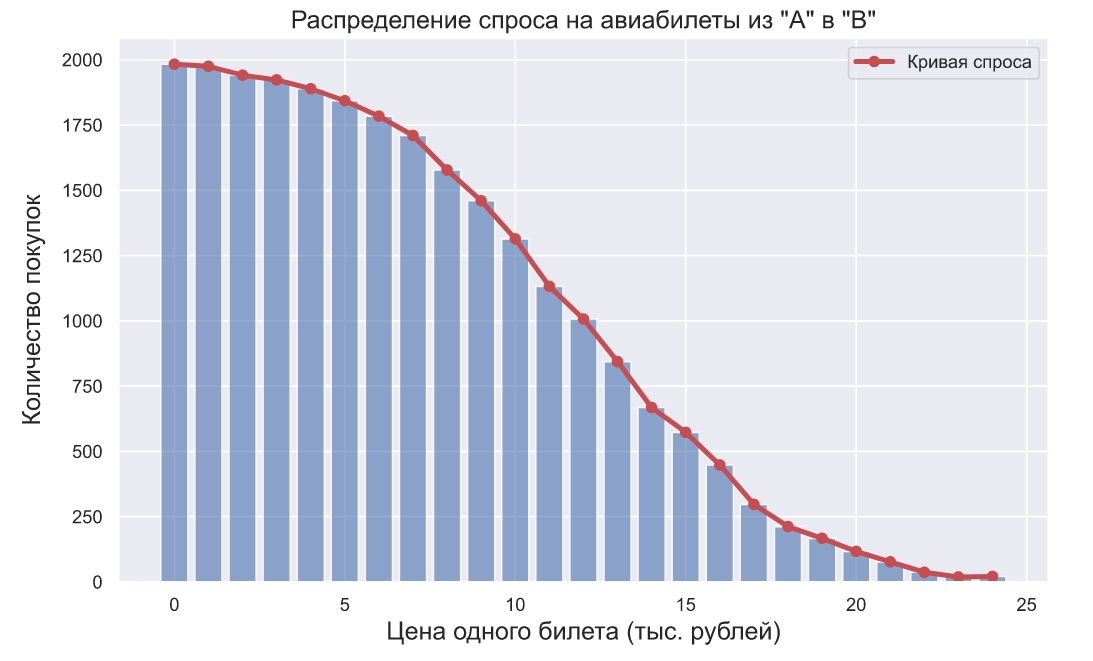
Представим совсем нереалистичную ситуацию, в которой некоторая авиакомпания решила найти оптимальную стоимость авиабилетов из «A» в «B». Не реалистичность будет заключаться в том, что спрос на авиабилеты будет стационарным, а в авиакомпании решили пойти на беспрецедентный эксперимент — изменять стоимость билетов от 0 до 25 тысяч рублей, увеличивая значение цены на 1 тысячу рублей после каждых 2000 тысяч посетителей. После такого эксперимента, можно было бы наблюдать следующую картину:
Оптимальную цену авиабилета можно было бы найти исходя из максимизации выручки, обозначим -ю цену как
-ю цену как  а спрос при данной цене (количество купленных авиабилетов) как
а спрос при данной цене (количество купленных авиабилетов) как  , тогда для максимизации выручки нам нужно найти такую цену
, тогда для максимизации выручки нам нужно найти такую цену  при которой произведение
при которой произведение  на
на  окажется самым большим, то есть
окажется самым большим, то есть

что можно изобразить на следующем графике:
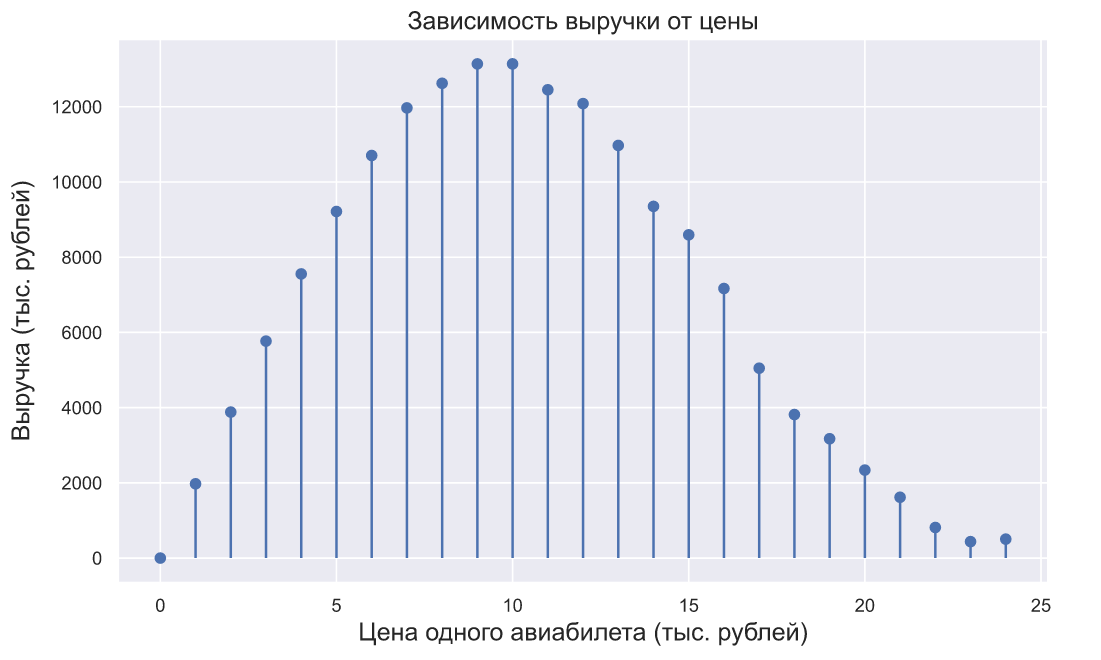
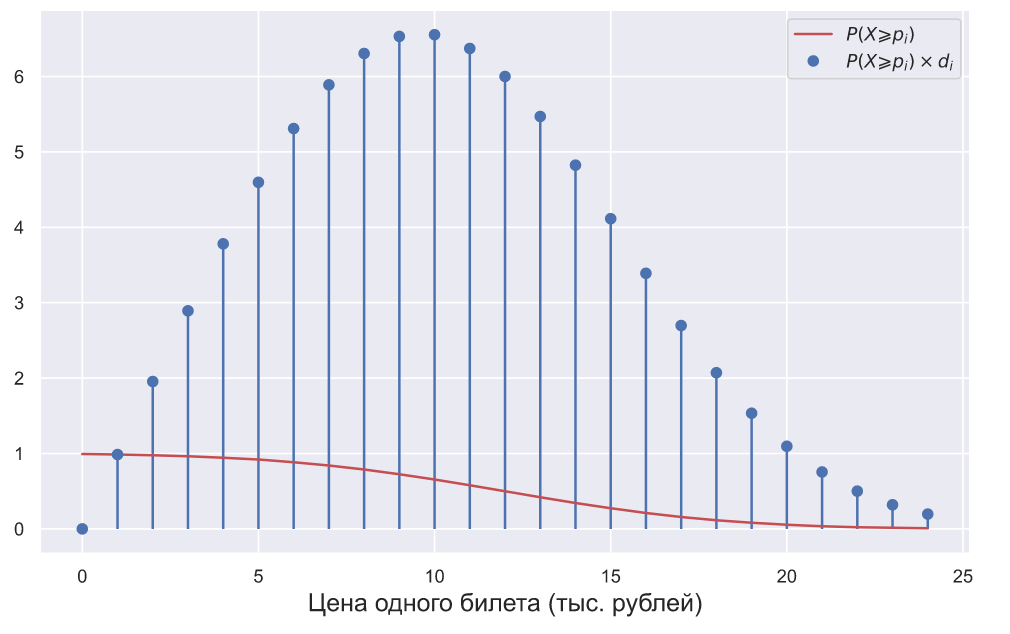
Если бы в авиакомпании взглянули на этот график, то вполне могли бы решить, что оптимальная цена авиабилетов составляет 10 тысяч рублей.
Но что если бы в авиакомпании изначально знали, о том что спрос на билеты распределен как ? Очевидно, что в этом случае они могли бы вычислить вероятность покупки одного билета при его определенной стоимости. Обозначим количество денег которое покупатель готов заплатить за один билет символом
? Очевидно, что в этом случае они могли бы вычислить вероятность покупки одного билета при его определенной стоимости. Обозначим количество денег которое покупатель готов заплатить за один билет символом  , тогда вероятность того, что покупатель его купит можно вычислить по следующей формуле:
, тогда вероятность того, что покупатель его купит можно вычислить по следующей формуле:

где — функция плотности вероятности нормального распределения, а
— функция плотности вероятности нормального распределения, а  — пробегает по всем допустимым значениям цен. Затем, чтобы получить значение оптимальной цены, достаточно умножить полученные значения вероятностей на соответствующие им цены, то есть оптимальная цена может быть найдена как
— пробегает по всем допустимым значениям цен. Затем, чтобы получить значение оптимальной цены, достаточно умножить полученные значения вероятностей на соответствующие им цены, то есть оптимальная цена может быть найдена как

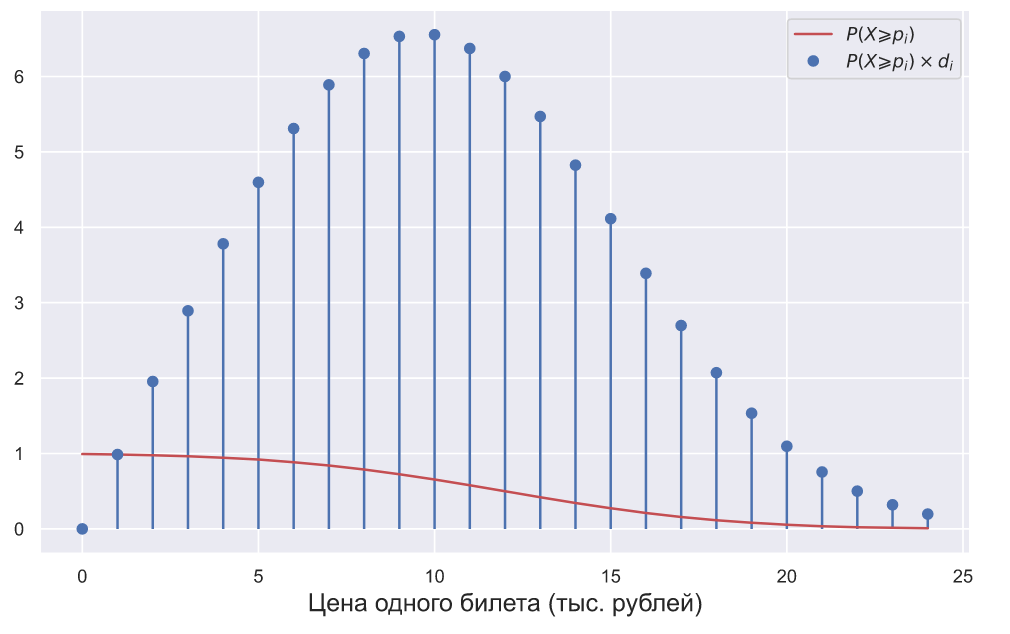
Давайте изобразим это на графике:
Получается, что кривая спроса может быть получена на основе распределения его плотности вероятности. Тогда возникает вполне закономерный вопрос: почему мы практически всегда пытаемся определить именно кривую спроса, но обделяем вниманием его распределение? На этот вопрос непросто ответить, но можно предположить, что пристальное внимание именно к кривой спроса обусловлено тем, что все началось в эпоху офлайн продаж, а дальше все двигалось по инерции. Например, в обычном магазине вполне возможно посчитать количество посетителей, но нет возможности оценить количество посетителей заинтересованных в каком-то конкретном товаре. В этом случае оценка вероятности продажи одной единицы конкретного товара сильно осложняется. В офлайне гораздо проще и логичнее воспринимать количество проданного товара в некоторый промежуток времени, как случайную величину из Пуассоновского распределения. Можно вообще не вести подсчет посетителей и учитывать только количество единиц проданного товара:

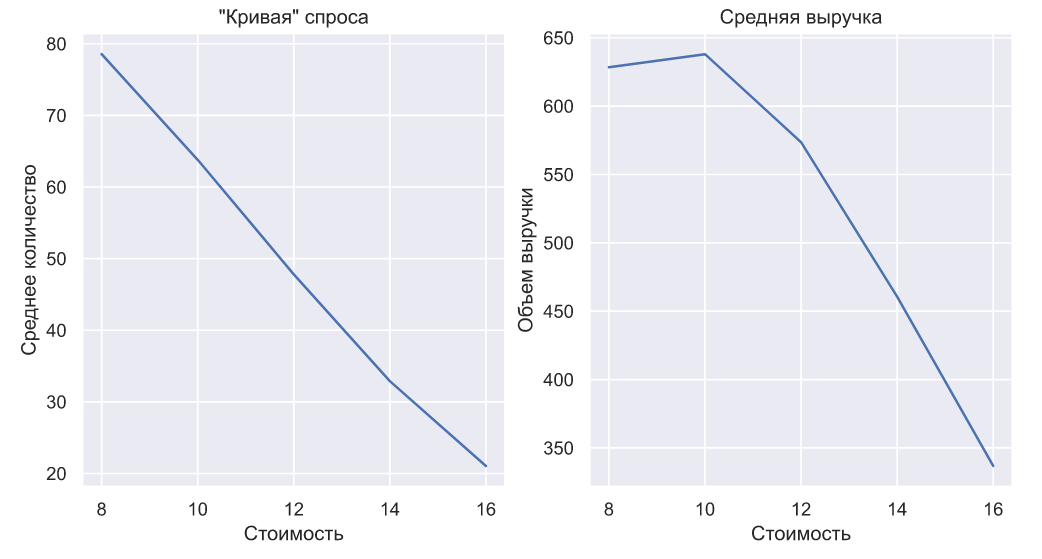
На вышеприведенном графике показано как могли бы выглядеть такие продажи авиабилетов при разной цене, где черной линией показано среднее значение продаж в каждом периоде. Именно благодаря средним значениям мы можем построить кривую спроса и определить оптимальную стоимость:
Получается, что информация о продажах в офлайне позволяет оценивать только кривую спроса и ее недостаточно для того чтобы оценить его распределение. Но что если продажи переместятся в онлайн и теперь для того, что бы узнать стоимость некоторого товара, допустим, того же авиабилета и, уж тем более, приобрести его, придется зайти на отдельную страничку интернет-магазина (да, для авиабилета уже так происходит, но может не происходит для других товаров или услуг: к примеру, если мы говорим о b2b логистике)? Появится ли у нас информация, которой будет достаточно для оценки распределения?
Допустим страницу с авиабилетом по направлению «A-B» посетили 20 человек, если спрос распределен как , то мы можем смоделировать значения случайной величины
, то мы можем смоделировать значения случайной величины  — максимальную стоимость авиабилета, которую может себе позволить посетитель:
— максимальную стоимость авиабилета, которую может себе позволить посетитель:
Если бы существовал какой-то волшебный способ получить такую выборку, то, даже несмотря на ее крошечный объем, можно все равно получить более-менее правдоподобные оценки параметров распределения:
Но волшебства не существует, и все что нам остается это устанавливать и менять цену, наблюдая сколько посетителей совершит или не совершит покупку. Если каждый из 20 смоделированных выше посетителей увидит, что билет стоит 11 тысяч рублей, то единственное, что мы узнаем в итоге, это то, что:
Кажется что цена — это просто цена, тем не менее, можно задать простой вопрос: чем цена на товар в офлайне отличается от той же самой цены в онлайне? Пусть случайная величина показывает совершил посетитель покупку или нет, т.е. принимает всего два значения: 1 — покупка совершена и 0 — покупка не совершена, тогда оценка вероятности продажи одной единицы товара, в нашем случае — авиабилета, может быть вычислена по следующей формуле:
показывает совершил посетитель покупку или нет, т.е. принимает всего два значения: 1 — покупка совершена и 0 — покупка не совершена, тогда оценка вероятности продажи одной единицы товара, в нашем случае — авиабилета, может быть вычислена по следующей формуле:

где — это количество единиц, а
— это количество единиц, а  — количество нулей.
— количество нулей.
После того как мы получили оценку вероятности продажи одной единицы товара, цена перестала быть просто ценой, ведь теперь 0.45-квантиль величины равен 11 тысячи рублей, причем
равен 11 тысячи рублей, причем  — это оцениваемый нами уровень данного квантиля:
— это оцениваемый нами уровень данного квантиля:

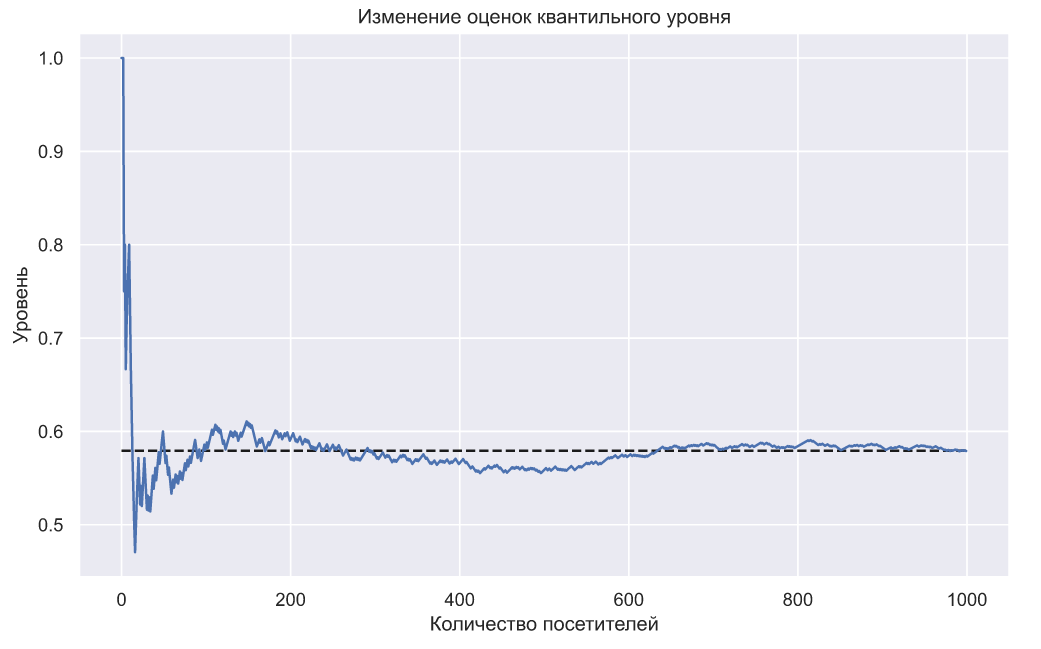
Значение квантиля показывает нам с какой вероятность значение не превысит 11 тысяч рублей, по нашим скромным оценкам эта вероятность равна 0.45 (на самом деле, чтобы вписаться в определение квантиля, мы должны считать квантилем не 11, а 10.99 тысяч рублей, но это не критично в данном случае). Чем больше людей посетят страницу по продаже билетов с ценой в 11 тысяч рублей, тем точнее будут оценки квантильного уровня:
не превысит 11 тысяч рублей, по нашим скромным оценкам эта вероятность равна 0.45 (на самом деле, чтобы вписаться в определение квантиля, мы должны считать квантилем не 11, а 10.99 тысяч рублей, но это не критично в данном случае). Чем больше людей посетят страницу по продаже билетов с ценой в 11 тысяч рублей, тем точнее будут оценки квантильного уровня:

В пределе значение должно стремиться к
должно стремиться к  — истинному значению вероятности продажи одной единицы товара, которая на графике обозначена черной пунктирной линией. В определенных ситуациях, даже этой единственной оценки уже достаточно, чтобы понять насколько выбранная нами цена является оптимальной. Например, если вероятность покупки очень большая, то, очевидно, что цена занижена и наоборот, если покупают слишком мало, то цена завышена. Если нам необходимо продавать какое-то определенное количество товара, то зная среднюю посещаемость, можно сразу понять является ли цена оптимальной или нет. Получается, что даже из первой полученной оценки можно попробовать извлечь хоть какую-то полезную информацию. Но давайте вернемся к оценке параметров распределения спроса.
— истинному значению вероятности продажи одной единицы товара, которая на графике обозначена черной пунктирной линией. В определенных ситуациях, даже этой единственной оценки уже достаточно, чтобы понять насколько выбранная нами цена является оптимальной. Например, если вероятность покупки очень большая, то, очевидно, что цена занижена и наоборот, если покупают слишком мало, то цена завышена. Если нам необходимо продавать какое-то определенное количество товара, то зная среднюю посещаемость, можно сразу понять является ли цена оптимальной или нет. Получается, что даже из первой полученной оценки можно попробовать извлечь хоть какую-то полезную информацию. Но давайте вернемся к оценке параметров распределения спроса.
Величина имеет распределение Бернулли, тогда величина
имеет распределение Бернулли, тогда величина  — количество проданного товара
— количество проданного товара  посетителям подчиняется биномиальному закону распределения:
посетителям подчиняется биномиальному закону распределения:


Если предположить, что — оценка вероятности продажи одной единицы товара по цене
— оценка вероятности продажи одной единицы товара по цене  приближенно равна истинному значению этой вероятности
приближенно равна истинному значению этой вероятности  то можно записать следующее:
то можно записать следующее:

а это значит, что на основе мы можем получить оценки параметров распределения спроса
мы можем получить оценки параметров распределения спроса  и
и  .
.
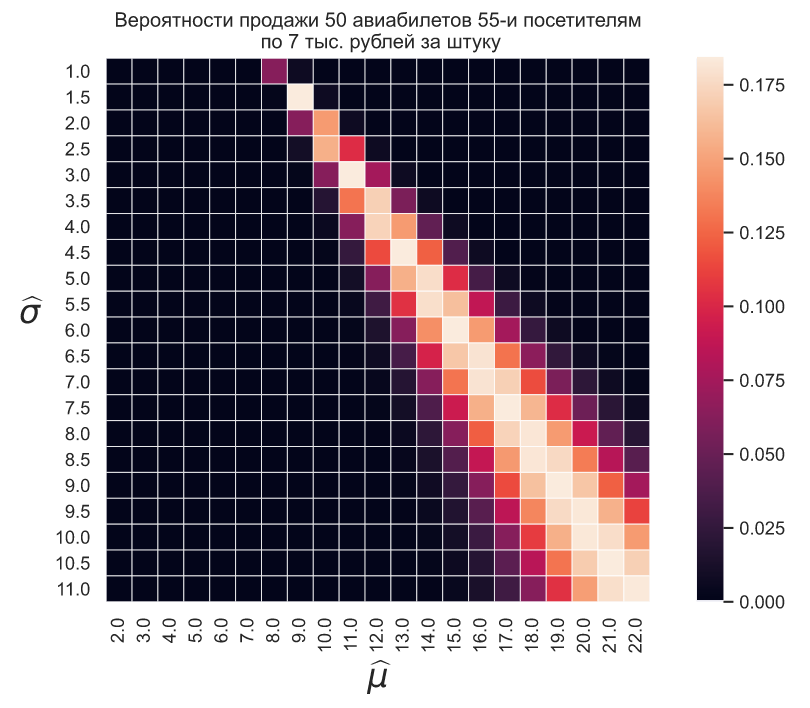
Допустим мы установили стоимость авиабилета в 7 тысяч рублей, представим, что в течение для его купили 50 посетителей из 55, пусть
![$\widehat{\mu} \in [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22]$](https://habrastorage.org/getpro/habr/formulas/9f4/af5/8b0/9f4af58b0f7eb150df3148c5fd587c9d.svg)
и
![$\widehat{\sigma} \in [1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5, 5.5, 6, 6.5, 7, 7.5, 8, 8.5, 9, 9.5, 10, 10.5, 11],$](https://habrastorage.org/getpro/habr/formulas/446/d35/399/446d3539913a80cb65e58f051e004642.svg)
тогда мы можем оценить вероятность продажи 50-и авиабилетов 55-и посетителям для разных значений и
и  как
как

Изобразим данные оценки в виде тепловой карты:
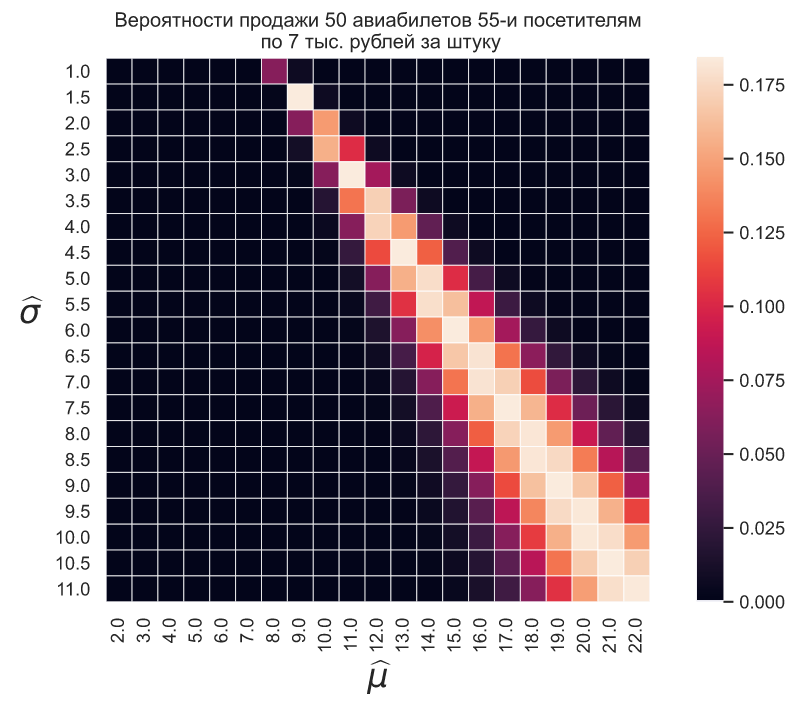
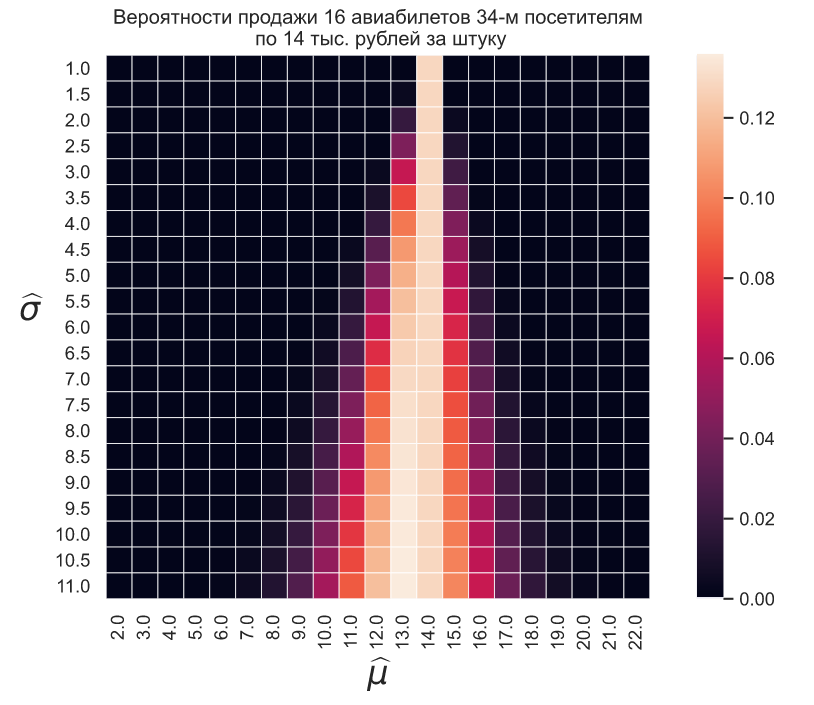
Если в следующий день установить стоимость в 14 тысяч рублей и представить, что было продано 16 билетов 34-м посетителям, то тепловая карта будет выглядеть так:

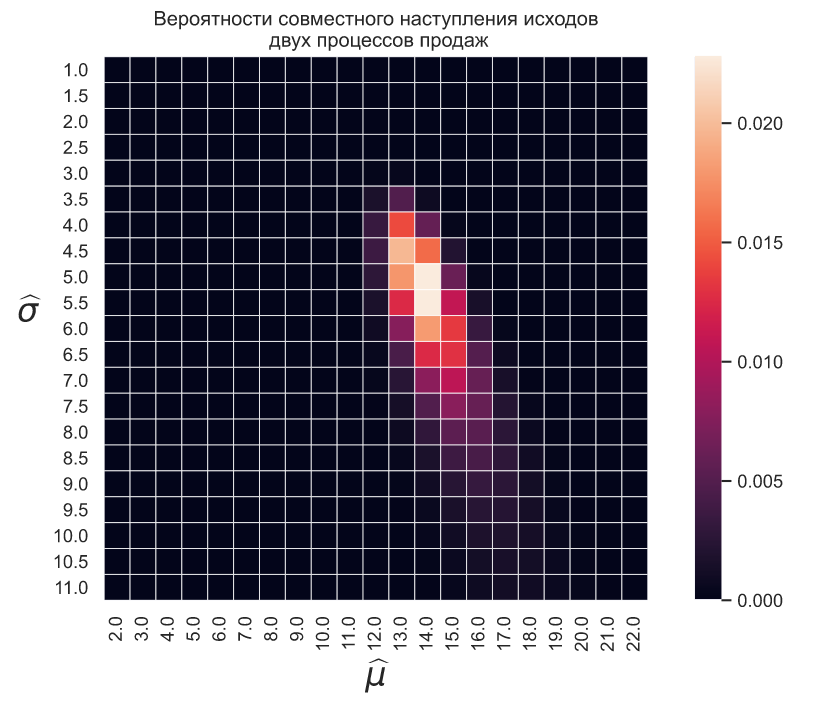
Имея всего два квантиля мы можем оценить вероятность совместного наступления двух исходов как простое произведение вероятностей их отдельного наступления:
При наличии некоторого количества квантилей мы можем найти наилучшие оценки и
и  для их истинных значений из условия максимального правдоподобия, т.е.
для их истинных значений из условия максимального правдоподобия, т.е.

Например, двух вышеприведенных квантилей достаточно чтобы получить первые оценки параметров распределения спроса, а значит — приступить к процессу максимизации выручки:

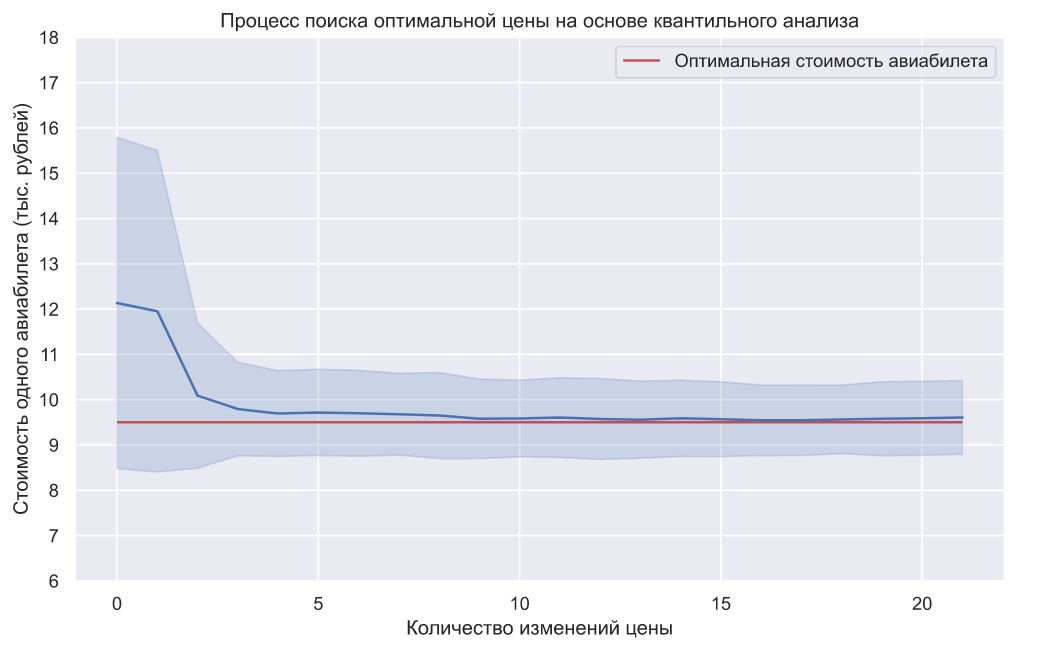
Мы можем повторить данный эксперимент 100 раз и взглянуть на динамику усредненных значений:
На графике показано среднее значение цены и ее стандартное отклонение. Взглянем на объем выручки в каждом эксперименте:

Теперь для сравнения попробуем найти оптимальную стоимость с помощью алгоритма сэмплирования Томпсона (TS). Что бы провести более-менее корректное сравнение, выясним сколько в среднем посетителей участвовало в одном эксперименте на основе квантильного анализа:
Округлим это значение до 1000 и точно так же повторим эксперимент 100 раз:

И так же взглянем на объем выручки в каждом эксперименте:

Преимущества квантильного анализа перед TS алгоритмом очевидны:
— более быстрая сходимость;
— гораздо меньшее количество изменений цены;
— незначительное, но все же, увеличение объема выручки.
Разумеется, результаты сравнения выглядят немного подозрительными и для сомнений в их корректности есть основания. Во-первых, алгоритм TS это эвристика, а это значит, что мы можем оптимизировать его множеством самых разных способов. Например, мы можем использовать наши некоторые представления о кривой спроса и перед запуском установить параметры и
и  в соответствующие этим представлениям значения. Мы можем пойти еще дальше и использовать еще больше предметно-ориентированных знаний и создать что-то вроде алгоритма-советника, который помогал бы принимать более правильные решения по установке и изменению цен. Но все это не приведет к желаемому результату, потому что основная причина такого результата кроется в количестве проверяемых цен:
в соответствующие этим представлениям значения. Мы можем пойти еще дальше и использовать еще больше предметно-ориентированных знаний и создать что-то вроде алгоритма-советника, который помогал бы принимать более правильные решения по установке и изменению цен. Но все это не приведет к желаемому результату, потому что основная причина такого результата кроется в количестве проверяемых цен:
![$\textrm{prices} \in [6,6.5,7,7.5,8,8.5,9,9.5,10,10.5,11,11.5,12,12.5,13,13.5,14,14.5,15,15.5,16,16.5,17,17.5,18].$](https://habrastorage.org/getpro/habr/formulas/201/452/4b7/2014524b753fe3952e1d23685a5abd69.svg)
На первый взгляд, в таком количестве цен для продажи большинства товаров нет никакой логики. Гораздо лучше и логичнее поступить так, как это принято — использовать меньшее количество цен, например:
![$\textrm{prices} \in [7.99, 8.99, 9.99, 10.99, 11.99].$](https://habrastorage.org/getpro/habr/formulas/1a9/77c/ac2/1a977cac2cf20bea49d0fdc767870c52.svg)
В этом случае TS алгоритм будет работать просто идеально. Но что если оптимальная цена равна 9.5 тысяч рублей? В случае небольших объемов продаж это не критично, но если объемы продаж велики, то это негативно скажется на прибыли. Основное требование к продаже авиабилетов как раз и заключается в том, что количество проверяемых цен должно быть максимально большим. А что если спрос изменится и оптимальная цена вообще покинет установленный диапазон цен? Это означает, что мы все равно должны как-то учитывать цены за пределами выбранного диапазона, т.е. так или иначе цен становится еще больше. Конечно, вышеприведенные эксперименты предполагали стационарность спроса на авиабилеты, который в действительности является динамическим. Алгоритм TS может быть модифицирован для работы с изменяющимся спросом. Суть модификации заключается в ограничении параметров и
и  какими-то максимальными значениями — чем меньше эти значения, тем быстрее TS реагирует на изменение. В то же самое время, чем меньше ограничивающие значения, тем больше уклон на исследования цен. Кстати процесс исследования цен, это тоже отдельная и очень большая проблема, связанная с тем, что мы не можем менять цену после каждого посетителя. А это значит, что если мы выбрали какую-то, пусть даже самую неоптимальную цену, то все равно придется продержать ее какое-то время иначе это неизбежно приведет к появлению противоречивого опыта у некоторых посетителей.
какими-то максимальными значениями — чем меньше эти значения, тем быстрее TS реагирует на изменение. В то же самое время, чем меньше ограничивающие значения, тем больше уклон на исследования цен. Кстати процесс исследования цен, это тоже отдельная и очень большая проблема, связанная с тем, что мы не можем менять цену после каждого посетителя. А это значит, что если мы выбрали какую-то, пусть даже самую неоптимальную цену, то все равно придется продержать ее какое-то время иначе это неизбежно приведет к появлению противоречивого опыта у некоторых посетителей.
Все вышеперечисленные трудности можно преодолеть с разной степенью успеха благодаря множеству модификаций TS алгоритма. Но самая главная проблема заключается в том, что данные о продажах, появляющиеся в ходе его работы абсолютно непригодны для решения задачи глобальной оптимизации. Ведь в действительности, даже имея на руках самый идеальный алгоритм ценообразования, от него не будет абсолютно никакого толка если авиакомпания не выполнит оптимальную расстановку авиапарка по маршрутам. В свою очередь, от алгоритмов ценообразования и расстановки авиапарка также не будет никакой пользы, если авиакомпании не будут иметь согласованных стратегий (для общего эффекта на отрасль в короткие сроки; если же стратегии не согласованы, то рынок бы тоже выровнялся со временем при внедрении алгоритмов хотя бы одной авиакомпанией, но, к сожалению, отрасль является в том или ином виде дотационной во многих странах мира, что сильно ограничивает возможности саморегулирования). А ведь помимо авиакомпаний в системе присутствуют и другие игроки, например, поставщики топлива и аэропорты, чьи действия могут свести на нет даже самую оптимальную стратегию авиакомпаний. Это чрезвычайно сложная система, которая, как это ни странно, существует в основном только за счет кошельков конечных потребителей. Поэтому единственный способ начать оптимизацию всей системы — это начать с ценообразования.
Например, суть расстановки авиапарка заключается в том, что мы должны постоянно принимать управляющие решения о назначении самолетов конкретного типа на конкретные маршруты, для чего необходима информация хотя бы о кривой спроса. Если использовать самую идеальную реализацию TS алгоритма, которая с первых попыток находит оптимальную цену, то окажется что для восстановления кривой спроса просто не окажется нужных данных по другим ценам. Сначала это не кажется проблемой, ведь у нас есть идеальный алгоритм ценообразования, но в этой ситуации алгоритм глобальной оптимизации тоже становится эвристическим, т.е. для того что бы понять, что какому-то самолету не стоит летать по данному направлению, придется понести серьезные убытки. Наличие кривых спроса, наоборот, позволяет без всяких экспериментов сразу менять маршруты и расписания с минимальными убытками.
Квантильный анализ требует установки всего двух исследуемых цен, которые могут выбираться как случайно, так и на основе имеющейся аналитики. Все последующие изменения делаются только на основе уточняющихся оценок параметров распределения спроса. Это означает, что квантильный анализ не является эвристическим и, каким бы ни было количество возможных цен, исследоваться будут только те цены, которые считаются оптимальными на данном этапе. И самое главное, появляющиеся после каждого очередного квантиля оценки, могут быть использованы в многоэтапных задачах стохастической оптимизации. Казалось бы — все круто. Но у квантильного анализа есть один существенный минус — непонятно каким должен быть объем выборки, т.е. непонятно сколько нужно посетителей для того, чтобы оценка квантильного уровня была более-менее статистически значимой. Если использовать для оценки вероятности продажи одной единицы товара небольшое количество посетителей, то очевидно, что эта оценка будет обладать слишком большой дисперсией, и процесс поиска оптимальной цены слишком затянется. Если использовать слишком большое количество посетителей, то мы будем получать более точные значения
небольшое количество посетителей, то очевидно, что эта оценка будет обладать слишком большой дисперсией, и процесс поиска оптимальной цены слишком затянется. Если использовать слишком большое количество посетителей, то мы будем получать более точные значения  , но в том случае если
, но в том случае если  является далеко не оптимальной, то ее долгое использование может привести к катастрофически большим убыткам. Неопределенность объема выборки — это действительно серьезная проблема, и, пожалуй, единственный способ ее преодоления заключается в использовании последовательного статистического анализа.
является далеко не оптимальной, то ее долгое использование может привести к катастрофически большим убыткам. Неопределенность объема выборки — это действительно серьезная проблема, и, пожалуй, единственный способ ее преодоления заключается в использовании последовательного статистического анализа.
Последовательный статистический анализ Вальда
Первоначальные оценки параметров спроса могут быть как верными так и нет, это значит, что мы можем с первых попыток найти самую оптимальную цену, ну или по крайней мере близкую к ней. Убедиться в оптимальности цены довольно просто, ведь если оценки параметров спроса верны, то вычисленная вероятность продажи одной единицы товара не будет значительно отличаться от наблюдаемой
не будет значительно отличаться от наблюдаемой  . Допустим у нас есть оценка
. Допустим у нас есть оценка  , тогда мы можем выделить область безразличия, ограниченную значениями
, тогда мы можем выделить область безразличия, ограниченную значениями  и
и  . Если
. Если  , то мы не предпринимаем никаких действий по изменению цены и считаем, что наша оценка верна. В противном случае мы уточняем оценки параметров распределения спроса и на основе их уточненных значений меняем цену.
, то мы не предпринимаем никаких действий по изменению цены и считаем, что наша оценка верна. В противном случае мы уточняем оценки параметров распределения спроса и на основе их уточненных значений меняем цену.
Выдвинем основную гипотезу о том, что вероятность продажи одной единицы товара
о том, что вероятность продажи одной единицы товара  при выбранной цене равна
при выбранной цене равна  и одну конкурирующую гипотезу
и одну конкурирующую гипотезу  , заключающуюся в том, что на самом деле
, заключающуюся в том, что на самом деле  . При доказательстве гипотез мы можем совершить ошибки первого и второго рода, обозначаемые
. При доказательстве гипотез мы можем совершить ошибки первого и второго рода, обозначаемые  и
и  соответственно. Тогда, согласно правилам последовательного статистического анализа Вальда, мы можем выделить две критические области:
соответственно. Тогда, согласно правилам последовательного статистического анализа Вальда, мы можем выделить две критические области:

Мы можем принять гипотезу о том что
о том что  , если
, если

или принять гипотезу о том что
о том что  , если
, если

В случае когда

мы продолжаем торговлю.
Критерий Вальда включает в себя критерий Неймана-Пирсона как частный случай, то есть может обеспечить те же самые уровни ошибок и
и  , но при этом не требует фиксированного объема выборки. Чтобы продемонстрировать последовательный анализ в действии, предположим что ошибки первого рода обходятся гораздо дороже, чем ошибки второго рода, пусть
, но при этом не требует фиксированного объема выборки. Чтобы продемонстрировать последовательный анализ в действии, предположим что ошибки первого рода обходятся гораздо дороже, чем ошибки второго рода, пусть  и
и  . А вероятности
. А вероятности  и
и  будут равны 0.45 и 0.55 соответственно, тогда процесс тестирования гипотез может выглядеть так:
будут равны 0.45 и 0.55 соответственно, тогда процесс тестирования гипотез может выглядеть так:

Фиолетовой линией обозначен объем выборки, рассчитанный по критерию Неймана-Пирсона, а серой линией обозначено количество испытаний в критерии Вальда. На графике видно, что в этом конкретном случае потребовалось гораздо меньше испытаний, чем для критерия Неймана-Пирсона. Тем не менее иногда количество испытаний может превышать количество, требуемое для критерия Неймана-Пирсона:

Теперь проверим заданный уровень ошибок для α. Смоделируем 10000 последовательных анализов в предположении, что каждый посетитель может купить одну единицу товара с вероятностью равной 0.45. В этом случае мы должны всегда принимать нулевую гипотезу, но поскольку α=0.05, то критерий Вальда должен ошибаться примерно в 5% случаев:

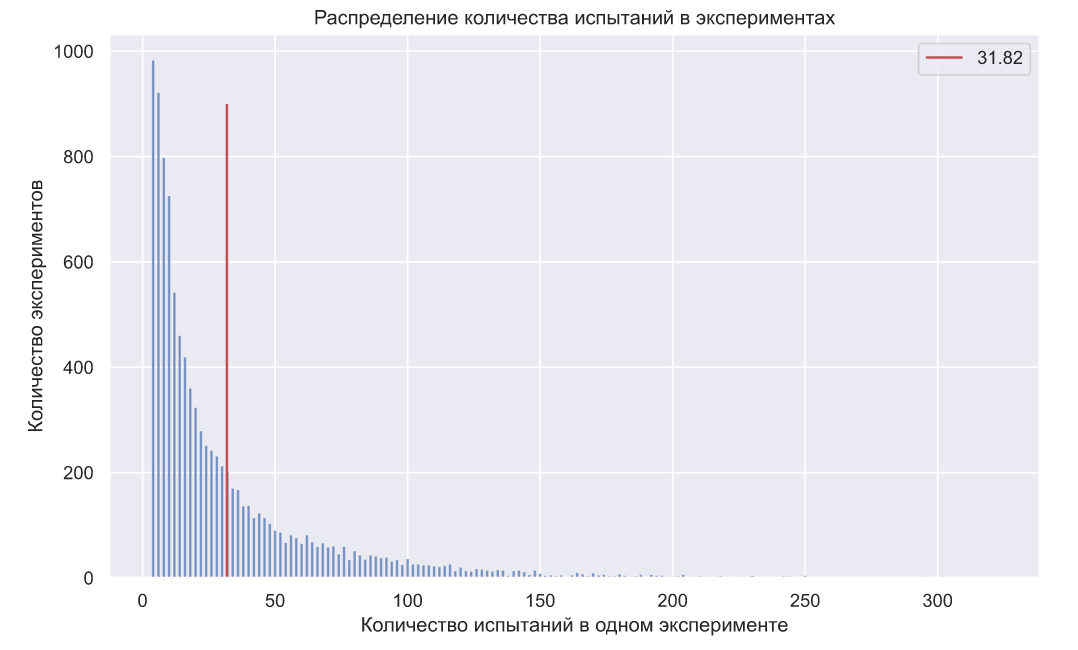
Вообще, в силу дискретной природы некоторых распределений и произвольных вещественных значений , можно увидеть некоторое отклонение фактического количества ошибок от заданного заранее уровня. Но если взглянуть на распределение количества испытаний в экспериментах, то становятся очевидны преимущества данного метода, так как в среднем он требует около 32 экспериментов (против 70 в критерии Неймана-Пирсона):
, можно увидеть некоторое отклонение фактического количества ошибок от заданного заранее уровня. Но если взглянуть на распределение количества испытаний в экспериментах, то становятся очевидны преимущества данного метода, так как в среднем он требует около 32 экспериментов (против 70 в критерии Неймана-Пирсона):
Выполним ту же проверку для ошибок второго рода ( ):
):

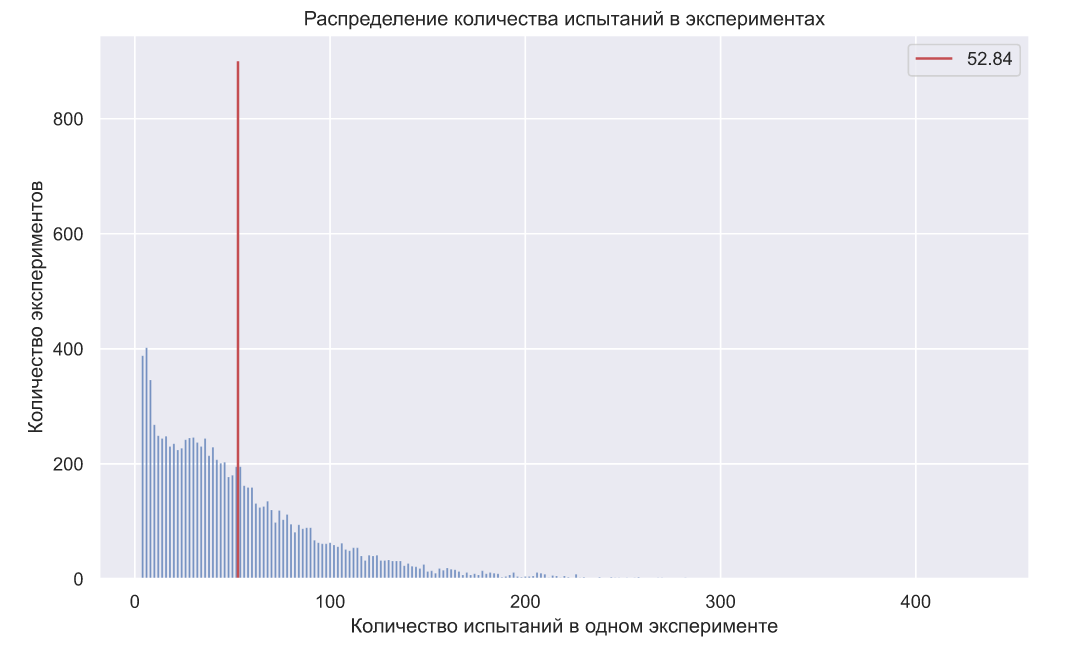
Полученное значение так же несколько отличается от заданного, что в общем-то согласуется с теорией, но распределение количества посетителей в экспериментах компенсирует такое отклонение:
так же несколько отличается от заданного, что в общем-то согласуется с теорией, но распределение количества посетителей в экспериментах компенсирует такое отклонение:
Большим преимуществом критерия Вальда является то, что чем сильнее мы ошибаемся в оценках параметров распределения спроса, тем меньше требуется посетителей для того, чтобы убедиться в этом. Следовательно, мы быстрее вычисляем новые оценки и на их основе определяем новую стоимость товара.
В качестве простой демонстрации того как критерий Вальда может быть использован предположим, что нам необходимо продать какое-то ограниченное количество товара в некоторый фиксированный промежуток времени. Пусть — это среднее количество посетителей в рассматриваемом промежутке времени, а
— это среднее количество посетителей в рассматриваемом промежутке времени, а  — это имеющееся количество единиц товара. Спрос распределен как
— это имеющееся количество единиц товара. Спрос распределен как  . Поскольку истинные параметры распределения спроса нам неизвестны, то и значение оптимальной цены для нас так же является неизвестной величиной. Можно подумать, что суть задачи заключается в поиске
. Поскольку истинные параметры распределения спроса нам неизвестны, то и значение оптимальной цены для нас так же является неизвестной величиной. Можно подумать, что суть задачи заключается в поиске  , но на самом деле первостепенной задачей является определение параметров спроса, а уже потом определение
, но на самом деле первостепенной задачей является определение параметров спроса, а уже потом определение  на их основе.
на их основе.
Для моделирования создадим несколько вспомогательных функций.
Работает данная функция очень просто: принимает значения имеющихся оценок параметров спроса, вычисляет вероятности продажи одной единицы товара по каждой из возможных цен, а затем выбирает наилучшую из них. Данная функция может определять цену несколько выше, чем та, благодаря которой можно продать весть товар. Например, если у нас есть 10 единиц товара, и по цене 10 у.е мы можем продать все, а по цене 12 у.е. — только 9 единиц, то функция вернет 12 у.е. потому что .
.
Генерируем одно значение из скрытого распределения спроса и если оно окажется больше установленной цены, то выдаем 1 — товар куплен; в противном случае выдаем 0 — товар не куплен.
Далее, нам понадобится реализация критерия Вальда:
В данной функции мы используем имеющуюся оценку вероятности продажи одной единицы товара — и после каждого посетителя применяем критерий Вальда, чтобы ответить на три нижеследующих вопроса:
и после каждого посетителя применяем критерий Вальда, чтобы ответить на три нижеследующих вопроса:
1. ?
?
2. ?
?
3. ?
?
Причем отвечать на эти вопросы мы должны с заранее заданным уровнем ошибок и
и  .
.
Далее каждый раз когда мы выходим за пределы мы должны предпринимать какие-то решения по поводу изменения цены. Несмотря на то, что оценки вероятности продажи одной единицы товара, получаемые с помощью относительных частот, испытывают очень сильные колебания из-за маленьких объемов выборок, мы все равно можем использовать эту информацию для создания оценок. По сути мы просто используем Байесовскую статистику — вычисляем вероятность получения совокупности наблюдаемых исходов в зависимости от разных предположений о параметрах спроса. Это очень накладно в вычислительном плане, зато работает:
мы должны предпринимать какие-то решения по поводу изменения цены. Несмотря на то, что оценки вероятности продажи одной единицы товара, получаемые с помощью относительных частот, испытывают очень сильные колебания из-за маленьких объемов выборок, мы все равно можем использовать эту информацию для создания оценок. По сути мы просто используем Байесовскую статистику — вычисляем вероятность получения совокупности наблюдаемых исходов в зависимости от разных предположений о параметрах спроса. Это очень накладно в вычислительном плане, зато работает:
Прежде чем переходить к моделированию процесса торговли сделаем некоторые уточнения. После установки начальной (самой первой) цены, ее коррекция происходит не на основе оценок параметров спроса, для которых пока просто не существует нужных данных, а в ручном режиме. Изменение происходит на некоторую величину, которая кажется наиболее целесообразной. В эксперименте она меняется на минимально возможное изменение цены (0.5 у.е.).
Еще одно замечание связано с тем, что в алгоритме задается максимально возможное изменение цены. Такая мера кажется целесообразной потому, что колебания относительных частот могут иметь очень сильные отклонения, но из-за таких «флуктуаций» относительной частоты изменение цены может быть просто катастрофически неверным. В эксперименте максимальная дельта цены равна 1.5 у.е.
Что бы провести эксперимент, создадим следующую функцию:
Итак, проведем эксперимент исходя из следующих начальных условий: спрос распределен как , первоначальные представления о параметрах спроса (исходные оценки спроса):
, первоначальные представления о параметрах спроса (исходные оценки спроса):  ,
,  , исходное количество товара
, исходное количество товара  , среднее число посетителей за некоторый период времени
, среднее число посетителей за некоторый период времени  , ошибки первого и второго рода:
, ошибки первого и второго рода:  ,
,  :
:
Сначала взглянем на то, как работает последовательный анализ Вальда и как он взаимосвязан с изменением интервала![$[p_{0}; p_{1}]$](https://habrastorage.org/getpro/habr/formulas/fc9/ede/a40/fc9edea400279d3bbb719fedcb9b8736.svg) . А что бы можно было хоть что-то разглядеть построим его для первых 200 посетителей:
. А что бы можно было хоть что-то разглядеть построим его для первых 200 посетителей:

Видно, что границы интервала меняются как только статистика, обозначенная черным цветом, пересекает критические значения (А — снизу, В — сверху).
На графике ниже можно наблюдать быструю сходимость оценок параметров распределения к истинным значениям, даже с учетом того, что наши первоначальные оценки были слишком занижены:

Полученные оценки позволяют достичь максимально возможных значений прибыли:

При этом цена одной единицы товара не испытывает сильных колебаний:

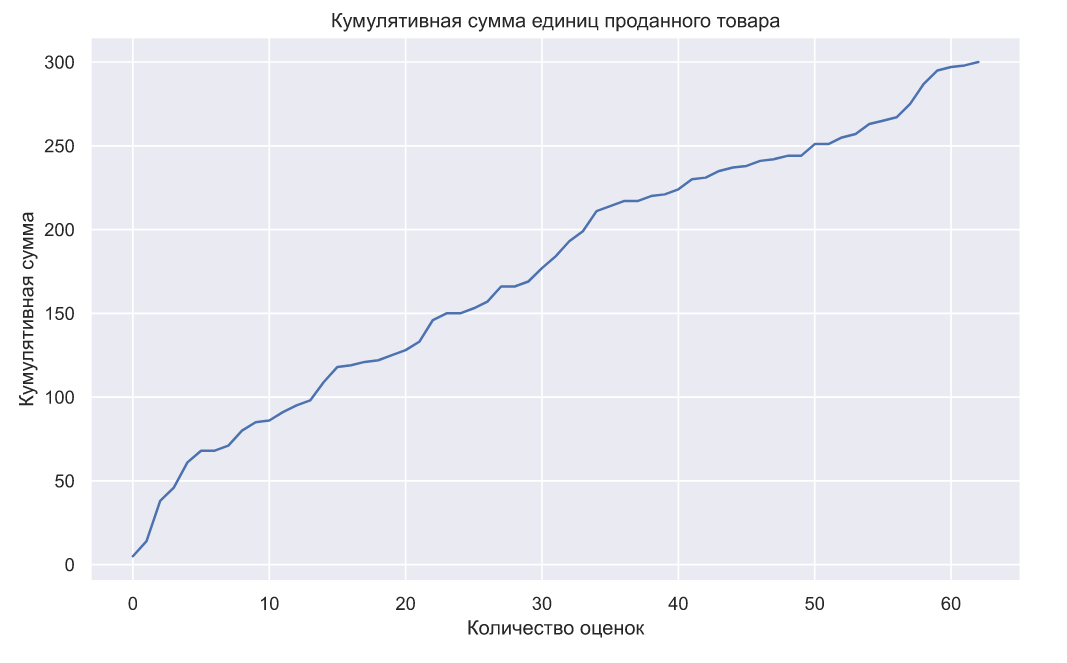
Ну и напоследок, можно видеть, что алгоритм успевает продать весь товар:
Наши первоначальные оценки параметров распределения спроса были довольно далеки от настоящих, но довольно быстро алгоритм все-таки нашел их правильные значения, и далее все продажи выполнялись по оптимальным ценам. Но самое главное в этом примере то, что благодаря критерию Вальда, мы смогли избавиться от фиксированного объема выборки, более того, благодаря параметрам и
и  , мы можем управлять статистической значимостью и мощностью выполняемого анализа. Это полезно еще и тем, что стоимость ошибок первого и второго рода может очень сильно отличаться, например, может быть гораздо выгоднее ошибиться и назначить более высокую стоимость товара, чем низкую. Так же данные параметры могут характеризовать склонность к риску, ведь если у нас есть какая-то аналитика предыдущих продаж, то мы можем сделать хорошие первоначальные оценки параметров распределения спроса, а значит можем рискнуть и с самого начала установить очень низкие значения
, мы можем управлять статистической значимостью и мощностью выполняемого анализа. Это полезно еще и тем, что стоимость ошибок первого и второго рода может очень сильно отличаться, например, может быть гораздо выгоднее ошибиться и назначить более высокую стоимость товара, чем низкую. Так же данные параметры могут характеризовать склонность к риску, ведь если у нас есть какая-то аналитика предыдущих продаж, то мы можем сделать хорошие первоначальные оценки параметров распределения спроса, а значит можем рискнуть и с самого начала установить очень низкие значения  и
и  . Так же данные параметры вовсе не обязаны быть статичными: допустим в начале продаж они могут быть довольно большими, а затем постепенно уменьшаться.
. Так же данные параметры вовсе не обязаны быть статичными: допустим в начале продаж они могут быть довольно большими, а затем постепенно уменьшаться.
В общем, как и в случае алгоритма семплирования Томпсона, представленный алгоритм на основе квантильного и последовательного анализа вовсе не являются универсальным рецептом оптимальных продаж, но принцип его работы на удивление прост и гибок, а это значит, что он может быть легко модифицирован и адаптирован под самые разные задачи. Давайте напоследок именно это и продемонстрируем.
Продажа авиабилетов при динамическом спросе
Стационарный спрос характерен для большого количества товаров, но не меньшее количество товаров характеризуется нестационарным спросом. Так же следует упомянуть, что понятие «оптимальная цена» может сильно меняться в зависимости от контекста. Например, для стационарного спроса оптимальность цены может зависеть от того, чего мы хотим добиться: продавать определенное количество товара, максимизировать валовую прибыль или выручку. Все это может учитываться и при нестационарном спросе, но могут появляться дополнительные требования, например, в ходе продаж может возникнуть срочная потребность в наличных деньгах или срочной распродаже товара. В конечном счете все эти требования к оптимальности цены могут быть учтены в алгоритме. Нас же теперь интересует как модифицировать алгоритм так, чтобы он мог учитывать динамику спроса.
Давайте снова рассмотрим какой-нибудь простой случай: пусть теперь спрос распределен как , где
, где  — это время. Такая модель спроса уже очень близка к тем ситуациям, когда спрос на некоторый товар меняется со временем (не обязательно линейно), например спрос на шампанское увеличивается к новому году, а спрос на фрукты, лежащие на прилавках, падает с каждым днем, потому что они портятся. Тоже самое можно сказать про билеты на культурные мероприятия и про авиабилеты. Естественно цена на такие товары тоже не может быть стационарной, просто потому, что это не выгодно как для продавцов, так и для покупателей.
— это время. Такая модель спроса уже очень близка к тем ситуациям, когда спрос на некоторый товар меняется со временем (не обязательно линейно), например спрос на шампанское увеличивается к новому году, а спрос на фрукты, лежащие на прилавках, падает с каждым днем, потому что они портятся. Тоже самое можно сказать про билеты на культурные мероприятия и про авиабилеты. Естественно цена на такие товары тоже не может быть стационарной, просто потому, что это не выгодно как для продавцов, так и для покупателей.
Для большей простоты пока предположим, что нам неизвестны только и
и  , но для эксперимента предположим, что
, но для эксперимента предположим, что  и
и  . Очень трудно представить более-менее реалистичную ситуацию, при которой нам известно значение
. Очень трудно представить более-менее реалистичную ситуацию, при которой нам известно значение  и неизвестно значение
и неизвестно значение  , но пока предположим, что это так и пусть
, но пока предположим, что это так и пусть  . Допустим мы торговали некоторым товаром в течении 5 дней, т.е.
. Допустим мы торговали некоторым товаром в течении 5 дней, т.е.  будет следующим массивом:
будет следующим массивом:
В каждый из дней мы устанавливали следующие цены:
Количество посетителей в каждый из дней было таким:
Согласно нашей модели, в каждый из дней были следующие значения мат. ожидания нормального распределения:
Тогда количество проданного товара может быть очень просто смоделировано следующим образом:
Теперь перейдем к неизвестным параметрам и
и  : предположим, что мы знаем более-менее реалистичные границы этих параметров, например
: предположим, что мы знаем более-менее реалистичные границы этих параметров, например ![$\epsilon \in [0.7; 1.3]$](https://habrastorage.org/getpro/habr/formulas/d62/a07/7e1/d62a077e11dcf3ba6dcc9d3a8e97e3fb.svg) а
а ![$\mu_{0} \in [15; 25]$](https://habrastorage.org/getpro/habr/formulas/571/e4f/258/571e4f25876015cdf65251503d9cf1b3.svg) . Тогда мы можем предположить, что
. Тогда мы можем предположить, что  может принимать следующие значения:
может принимать следующие значения:
А может быть любым из следующего массива:
может быть любым из следующего массива:
Тогда мы можем предположить, что если то мат. ожидание может меняться следующим образом:
то мат. ожидание может меняться следующим образом:
Каждый столбец в данном массиве показывает как могло бы меняться мат. ожидание с каждым днем, если бы . Теперь мы можем проверить вероятность получить имеющиеся значения количества проданных единиц товара по каждому столбцу:
. Теперь мы можем проверить вероятность получить имеющиеся значения количества проданных единиц товара по каждому столбцу:

На графике можем наблюдать, что только в столбцах близких к истинному значению наблюдаются максимальные значения. В этом можно убедиться, если изобразить произведение вероятностей (сумму логарифмов) в каждом столбце:
наблюдаются максимальные значения. В этом можно убедиться, если изобразить произведение вероятностей (сумму логарифмов) в каждом столбце:

Если построить подобные графики для всех , то можем наблюдать следующую картину:
, то можем наблюдать следующую картину:

На этом графике, конечно же, невозможно разглядеть максимумы, да и один эксперимент вовсе не показатель сходимости, поэтому проведем больше экспериментов и взглянем на усредненные значения максимумов отдельно:
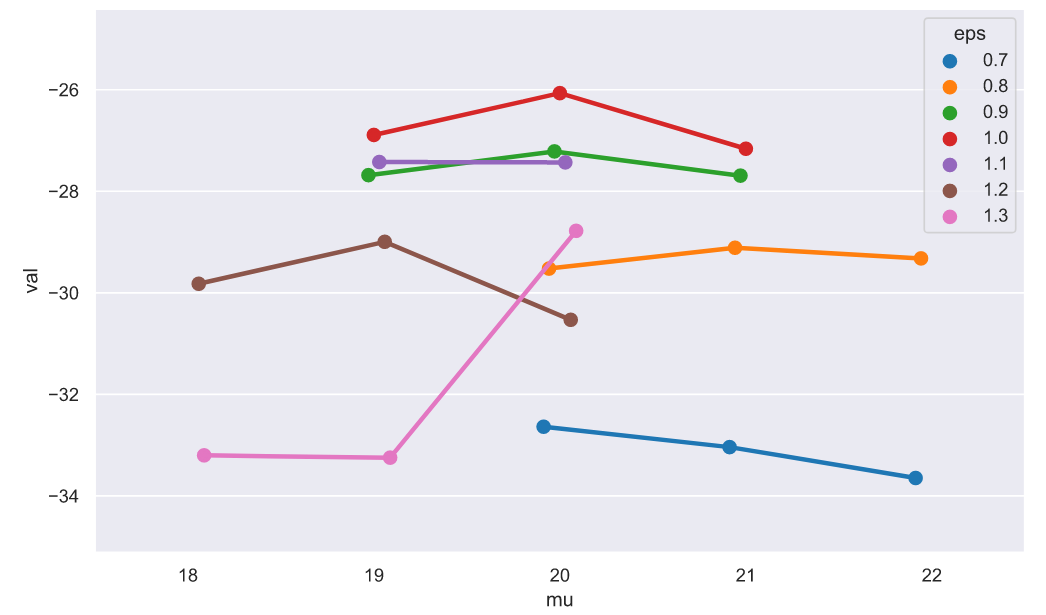
Как видим, наибольшие максимумы соответствуют значениям, которые близки к истинному значению . Разумеется, все это не строгое доказательство, но видно, что метод действительно сходится, поэтому давайте попробуем сделать модель по продаже билетов в условиях динамического спроса. Предположим, что нам нужно продать
. Разумеется, все это не строгое доказательство, но видно, что метод действительно сходится, поэтому давайте попробуем сделать модель по продаже билетов в условиях динамического спроса. Предположим, что нам нужно продать  билетов и продажи начинаются за 100 дней до вылета. Пусть количество посетителей будет распределено как
билетов и продажи начинаются за 100 дней до вылета. Пусть количество посетителей будет распределено как  , а спрос будет распределен как
, а спрос будет распределен как  , при этом будем считать, что пока закон изменения отклонения со временем является известным, т.е. в ходе продаж необходимо определить только закон изменения мат. ожидания. Если смоделировать данный спрос, то он будет выглядеть следующим образом:
, при этом будем считать, что пока закон изменения отклонения со временем является известным, т.е. в ходе продаж необходимо определить только закон изменения мат. ожидания. Если смоделировать данный спрос, то он будет выглядеть следующим образом:

По оси ординат отложена максимальная стоимость билета, выше которой посетитель не может совершить покупку. Допустим, что нам необходимо обеспечить равномерную продажу авиабилетов, т.е. на всем периоде продаж должны иметься доступные для покупки авиабилеты. Данное требование означает, что мы должны изменять цену так, чтобы вероятность продажи одного билета была неизменной на протяжении всего периода продаж. Для этого мы можем создать следующую простую функцию:
Благодаря этой функции мы будем оценивать прогнозируемую вероятность продажи одного билета на ближайшие сутки, а так же выяснять стоимость билета, на основе имеющихся оценок параметров и прогнозируемого количества посетителей. Теперь осталось определить всего две функции: одну для прогнозирования количества посетителей в ближайшие сутки (на основе простой линейной регрессии):
И еще одну для оценки параметров распределения спроса:
Взглянем как менялись выручка, стоимость билета и количество проданных билетов:

Это неплохой результат, который, кстати, был обеспечен не такими уж точными оценками параметров:

Можно еще раз задаться вопросом: зачем вообще нужен критерий Вальда? Ведь если выполнять квантильный анализ после каждого 25-го посетителя, то можно добиться практически тех же самых результатов:

Критерий Вальда нужен лишь для того, что бы задать уровень статистической значимости выводов о том где сейчас находится вероятность продажи одной единицы товара. Например, если мы склонны доверять имеющейся аналитике о параметрах распределения спроса, то можем значительно снизить уровни ошибок первого и второго рода, что будет равносильно увеличению фиксированного количества посетителей после которого выполняется квантильный анализ:

В данном случае мы можем наблюдать некоторое уменьшение выручки и уменьшение количества изменений цены (из-за которого, во многом, и произошло снижение выручки). Фактически, критерий Вальда даже не участвует в формировании цены, которым занимается квантильный анализ и нужен лишь для того, что бы определить частоту его выполнения. В критерии Неймана-Пирсона эта частота является фиксированной, но в критерии Вальда она зависит от величины ошибки, т.е. чем ошибочнее изменение цены, тем скорее оценка вероятности продажи одной единицы товара покинет зону безразличия, а значит мы скорее отреагируем на эту ошибку и попытаемся ее исправить. В данном примере трудно продемонстрировать достоинство такого поведения, потому что спрос хоть и является динамическим, но имеет стационарные приращения. Тем не менее, такая особенность критерия Вальда может оказаться особенно полезной для динамического спроса с нестационарными приращениями.
В определенной степени, уровни ошибок первого и второго рода в критерии Вальда можно отнести к классу гиперпараметров, т.е. параметров которые подбираются эмпирически.
Конечно, это крайне искусственный и очень простой пример, призванный показать, что критерий Вальда и квантильный анализ могут быть применены для динамического спроса. По мере приближения моделей к реальным условиям их сложность сильно возрастает. Например, выше мы договорились, что закон изменения отклонения с течением времени считается известным, но как быть если и он является неизвестным? Ответ на этот вопрос проще продемонстрировать. Предположим, что спрос зависит от времени и распределен как . Пусть
. Пусть  ,
,  ,
,  и
и  , тогда распределение 100000 посетителей будет выглядеть следующим образом:
, тогда распределение 100000 посетителей будет выглядеть следующим образом:

Данное распределение является смесью (суммой) бесконечного количества нормальных распределений и может быть задано следующим образом:
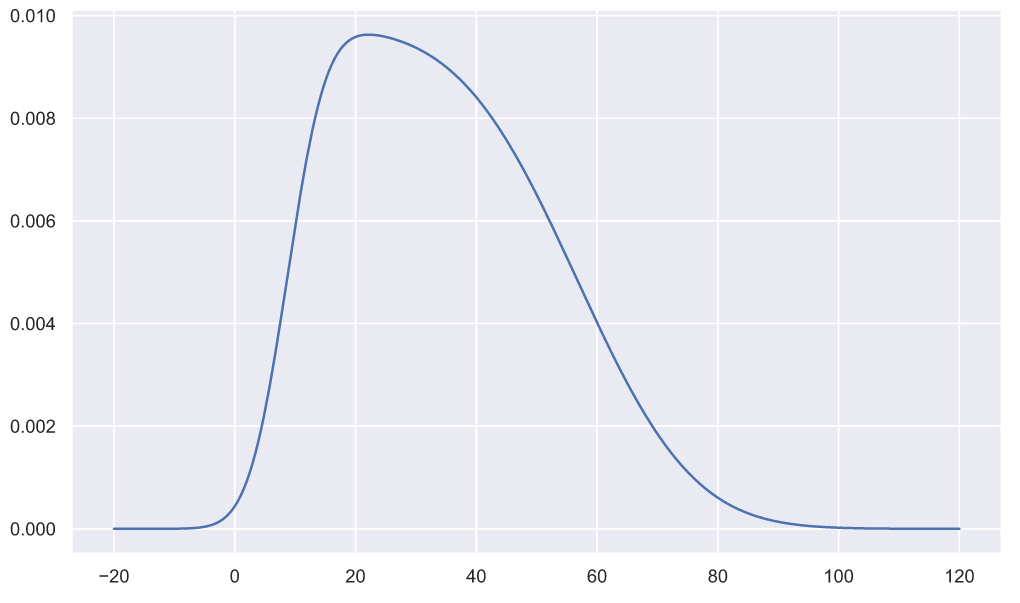
Это распределение является двухпараметрическим, т.е. оно так же как и нормальное распределение имеет параметры смещения и масштаба, но помимо них обладает еще двумя параметрами формы — ,
,  :
:

Если не рассматривать только фиксированные временные интервалы (например для вышеприведенного графика все распределения построены для![$t \in [0, 100]$](https://habrastorage.org/getpro/habr/formulas/8b2/c9b/86b/8b2c9b86b6d2346947ae10f78df31c73.svg) ), то границы интервалов так же будут влиять на форму распределений. Данное распределение может быть использовано в квантильном анализе, точно так же как выше использовалось нормальное. Причем мат. ожидание и отклонение вовсе не обязаны меняться со временем линейно, изменение может быть ускоренным или иметь другой более сложный вид. В общем случае, если мат. ожидание и отклонение модели спроса задаются как функции от времени, то вся задача сводится к оценке постоянных коэффициентов функций. Иными словами, оценка параметров по-прежнему опирается на Байесовский метод, просто количество измерений условных вероятностей теперь будет равно общему количеству параметров модели спроса.
), то границы интервалов так же будут влиять на форму распределений. Данное распределение может быть использовано в квантильном анализе, точно так же как выше использовалось нормальное. Причем мат. ожидание и отклонение вовсе не обязаны меняться со временем линейно, изменение может быть ускоренным или иметь другой более сложный вид. В общем случае, если мат. ожидание и отклонение модели спроса задаются как функции от времени, то вся задача сводится к оценке постоянных коэффициентов функций. Иными словами, оценка параметров по-прежнему опирается на Байесовский метод, просто количество измерений условных вероятностей теперь будет равно общему количеству параметров модели спроса.
В заключение
Если несколько раз (в данном случае 50) сравнивать работу данного алгоритма с текущим положением дел в ценообразовании авиабилетов, то картина получается следующая:
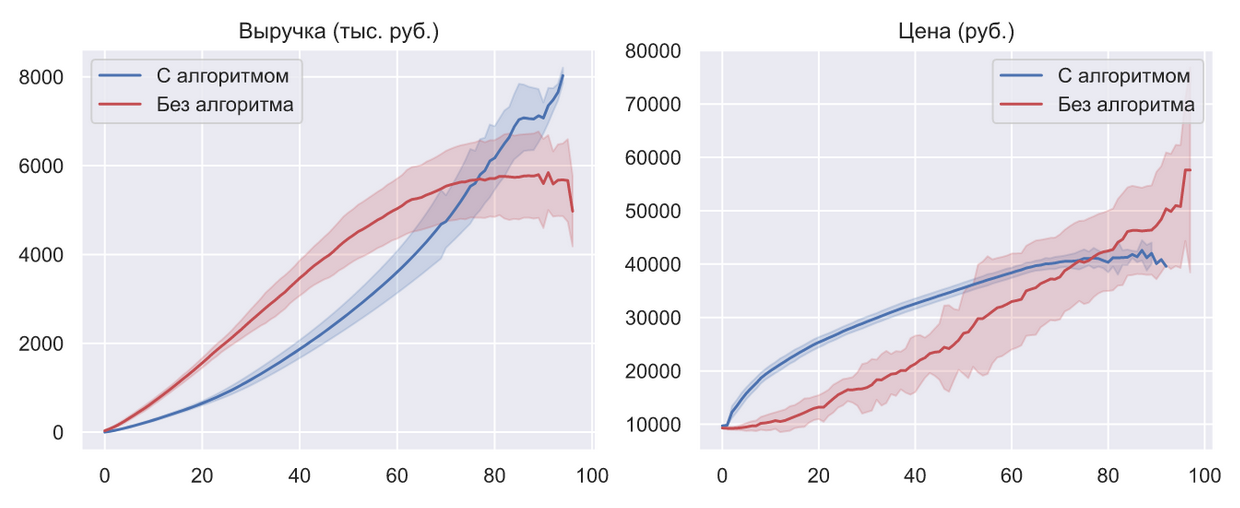
Линиями показаны мат. ожидания, а доверительные интервалы — это стандартные отклонения.
В данном случае под текущим положением дел понимается единственная и простейшая стратегия которая сейчас используется — ручное управление. С одной стороны может показаться, что такую стратегию практически невозможно смоделировать с учетом всей ее сложности. Однако, с определенной «высоты» (и с точки зрения конечного потребителя), вся эта система ведет себя как единственный продавец, который понимает все механизмы только на интуитивном уровне. Поскольку, в качестве цели мы ставили условие максимизации выручки при постоянном наличии билетов в продаже и их полной реализации, то все, что может делать данный продавец — менять цену, пытаясь выровнять скорость продажи билетов с учетом их оставшегося количества. В данном случае «менять цену» означает «угадать цену», т.е. изменение цены является случайной величиной из равномерного распределения, границы которого подобраны так, что бы стратегия удовлетворяла целевым условиям. Вот такая модель текущего положения дел.
Опять же, такое сравнение нельзя назвать абсолютно корректным, но оно дает возможность хотя бы приблизительно оценить прирост выручки обеспеченный ценообразованием на основе квантильного анализа, который можно оценить интервалом от 25% до 35%. Эти цифры вовсе неудивительны, поскольку в режиме ручного управления просто невозможно постоянно угадывать самую оптимальную цену. В случае единичных продаж без ручного управления не обойтись, но когда речь идет о масштабе целой авиакомпании — оно становится серьезным недостатком, который заставляет завышать стоимость билетов и терпеть серьезные убытки.
Вся данная статья базируется на одной простой гипотезе о том, что спрос имеет нормальное распределение. Казалось бы, на том же самом Kaggle полно данных по онлайн торговле и можно легко доказать или опровергнуть эту гипотезу. Но это не было целью данной статьи, так как проблема вовсе не в этом. Здесь мы хотели упрощенно продемонстрировать те подходы, которые используем при решении оптимизационных задач. В своем кругу мы иногда шутим, говоря, что статистическое управление — это то же самое, что управление автомобилем по зеркалу заднего вида, причем довольно маленькому и заляпанному. Ведь смысл оптимального управления заключается не только в том, чтобы найти лучшую стратегию, но еще и в том что бы выполнять ее оптимальную коррекцию на основе поступающих данных о спросе. Как раз коррекция и является самым слабым местом в управлении.
Безусловно, задача динамического ценообразования крайне актуальна для отрасли гражданских авиаперевозок, но как уже говорилось выше, даже если предположить, что у нее есть самое оптимальное решение, то от него все равно не будет никакого толка, если авиакомпания выполнит неоптимальную расстановку авиапарка или выберет для него неоптимальные маршруты. Представленный алгоритм ценообразования, при самых оптимистичных оценках позволяет добиться лишь 10%-го увеличения прибыли в сравнении с алгоритмом сэмплирования Томпсона. Это может показаться хорошим результатом, но на самом деле, если принять во внимание текущее положение дел глобальных логистических процессов, то эти 10% всего лишь капля в море той прибыли, которая упускается всеми игроками. Поэтому в следующей статье мы постараемся рассмотреть модели оптимизации использования судов, планирования расписания и формирования ценообразования как единую задачу.

Распределение спроса вместо кривой спроса
Переосмысление подхода к решению задачи началось, когда один из членов команды обратил внимание на предпринимателей розничной торговли, которые открывают социальные магазины. Это своеобразная форма благотворительности, которая заключается в том, что в магазине нет продавца, вместо которого есть что-то вроде ящика для пожертвований. В таком магазине можно взять любой товар с полки и самостоятельно решить сколько денег за него отдать. Все это конечно любопытно и наталкивает на множество размышлений, но примечательно то, что в подобных магазинах обычная кривая спроса превращается в некоторое распределение.
Что бы продемонстрировать это, а также все дальнейшие примеры мы будем использовать язык Python, поэтому сразу сделаем все необходимые импорты:
import numpy as np
np.random.seed(42)
import pandas as pd
from scipy import stats
from scipy.stats import norm, binom, bernoulli, poisson, beta
import matplotlib.pyplot as plt
from pylab import rcParams
rcParams['figure.figsize'] = 10, 6
%config InlineBackend.figure_format = 'svg'
import seaborn as sns
sns.set()
У нас нет данных о том сколько денег каждый посетитель подобного магазина платил за какой-то отдельно взятый товар, но это не помешает нам немного поразмышлять в этом направлении. Например, в знаменитом наборе данных tips отражена схожая ситуация, в которой посетителям ресторана нужно было самостоятельно принять решение о размере чаевых. Вряд ли в меню ресторана было большими красными буквами указано требование о том, что размер чаевых должен составлять 20% от стоимости заказа, но если взглянуть на график, то мы увидим, что значительная часть посетителей старается следовать этому негласному правилу:
tips = sns.load_dataset('tips')
sns.relplot(x='total_bill', y='tip', data=tips);
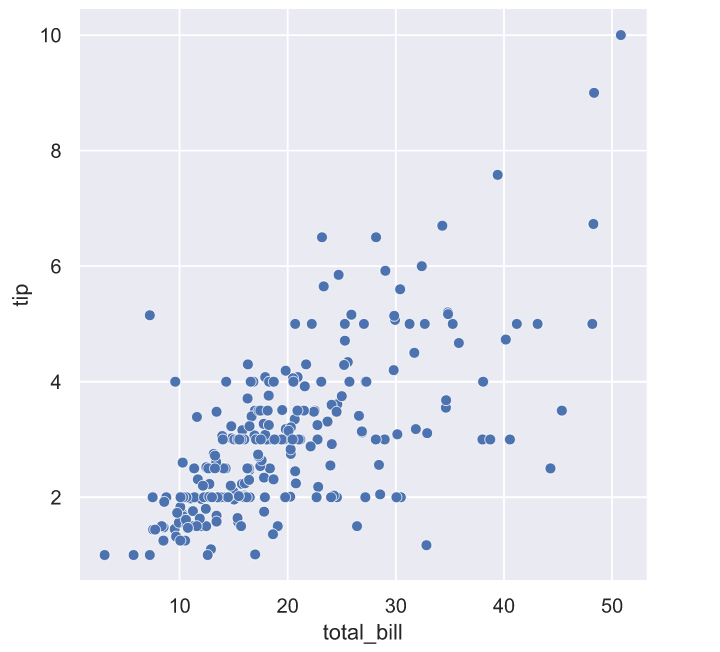
В какой-то мере это негласное правило можно считать социальной нормой. В любом случае, схожий механизм работает и в социальных магазинах: какая-то часть посетителей руководствуется чувством справедливости и старается платить столько, сколько указано на ценнике товара. В наборе данных tips можно оценить влияние других факторов на размер чаевых: день недели, время суток, пол человека, оплачивающего счет, или количество людей в группе, выполнившей заказ. Очевидно, что каждый посетитель социального магазина, так же может руководствоваться множеством самых разных факторов: уровень дохода и наличие работы, количество человек в семье, торопится он на данный момент или нет, есть кто-нибудь рядом или нет и т.д. По центральной предельной теореме распределение спроса на товар в таких магазинах можно считать предельно нормальным.
Если взять какой-нибудь конкретный товар в магазине без продавца, на ценнике которого указана стоимость в 12 рублей, то распределение спроса на него вполне могло бы выглядеть так:
Python
prices = np.r_[0: 35]
mu, sigma = 12, 5
demand = norm.rvs(mu, sigma, 1200)
sns.histplot(x=demand[demand > 0], discrete=True)
plt.title('Распределение спроса на некоторый товар в магазине без продавца', fontsize=15)
plt.xlabel('Цена', fontsize=15)
plt.ylabel('Количество покупок', fontsize=15, labelpad=10);

На самом деле мы можем лишь гадать как в действительности мог бы выглядеть этот график, так как у нас нет реальных данных. Но эти размышления наталкивают на мысль о том, что у спроса действительно должно быть какое-то распределение и, скорее всего, оно должно быть нормальным. В тоже самое время, если это действительно так, то это неизбежно должно приводить к тому, что какая-то часть распределения может оказаться в области отрицательных цен. Например, если бы мы опросили всех потенциальных покупателей некоторого города «A» о том, сколько они готовы заплатить за авиабилеты в город «B», ничего им не сообщая о его истинной стоимости, то вполне могли бы получить следующий результат:
Python
prices = np.r_[-10: 35]
mu, sigma = 12, 5
demand = norm.rvs(mu, sigma, 10000)
sns.histplot(demand, discrete=True)
plt.title('Распределение спроса в городе "A" на авиабилеты в город "B"', fontsize=15)
plt.xlabel('Цена (тыс. рублей)', fontsize=15)
plt.ylabel('Количество ответов', fontsize=15, labelpad=10);

С одной стороны, принятие во внимание отрицательных цен выглядит нелогичным и даже комичным. С другой стороны, вряд ли какая-то значительная часть читателей согласится слетать на выходные в Афганистан, даже если авиакомпания предложит за перелет приличную сумму денег. Так и во многих сферах коммерческой деятельности возможны ситуации, когда компании выгодно продавать свой товар или услуги по отрицательным ценам, чем не продавать вовсе. К примеру товар, который имеет ограниченный срок годности, после которого он должен быть утилизирован (бытовая химия, косметика, продукты питания) – компании проще отдать бесплатно или немного доплатить покупателям, чем оплачивать стоимость транспортировки и утилизации в дальнейшем. Попытка сэкономить и не утилизировать товар может привести к увеличению общих затрат компании, т.к. бесконечно хранить у себя на складах такие товары не получится. Это увеличивает стоимость логистик (складской), да и ресурсы складов не бесконечны. О примере продажи товаров с отрицательной ценой каждый слышал: цена нефти Brent опустилась ниже 0 в 2020 году. Но вернемся к распределению спроса: вовсе не обязательно, что какая-то часть спроса должна находиться в области отрицательных цен, но это действительно возможно, хотя бы потому что всегда могут найтись люди, которым определенный товар будет не нужен даже за значительную доплату.
Если спрос распределен нормально, то мы можем легко получить кривую спроса, для чего нужно просто начать продавать товар. Да, при более точном рассмотрении, обладая большим набором данных, мы можем прийти к тому, что спрос имеет другое распределение, но в первом приближении большинство методологий рекомендует начинать с нормального распределения, а дальше уже уточнять более сложными распределениями.
Представим совсем нереалистичную ситуацию, в которой некоторая авиакомпания решила найти оптимальную стоимость авиабилетов из «A» в «B». Не реалистичность будет заключаться в том, что спрос на авиабилеты будет стационарным, а в авиакомпании решили пойти на беспрецедентный эксперимент — изменять стоимость билетов от 0 до 25 тысяч рублей, увеличивая значение цены на 1 тысячу рублей после каждых 2000 тысяч посетителей. После такого эксперимента, можно было бы наблюдать следующую картину:
Python
np.random.seed(42)
prices = np.r_[0: 25]
mu, sigma = 12, 5
demand = [np.sum(norm.rvs(mu, sigma, 2000) > price) for price in prices]
plt.bar(prices, demand, alpha=0.6)
plt.plot(prices, demand, 'ro-', lw=3, label='Кривая спроса')
plt.title('Распределение спроса на авиабилеты из "A" в "B"', fontsize=15)
plt.xlabel('Цена одного билета (тыс. рублей)', fontsize=15)
plt.ylabel('Количество покупок', fontsize=15, labelpad=10)
plt.legend();

Оптимальную цену авиабилета можно было бы найти исходя из максимизации выручки, обозначим
что можно изобразить на следующем графике:
Python
plt.plot(prices, demand*prices, 'bo', lw=3)
plt.vlines(prices, 0, demand*prices)
plt.title('Зависимость выручки от цены', fontsize=15)
plt.xlabel('Цена одного авиабилета (тыс. рублей)', fontsize=15)
plt.ylabel('Выручка (тыс. рублей)', fontsize=15, labelpad=10);
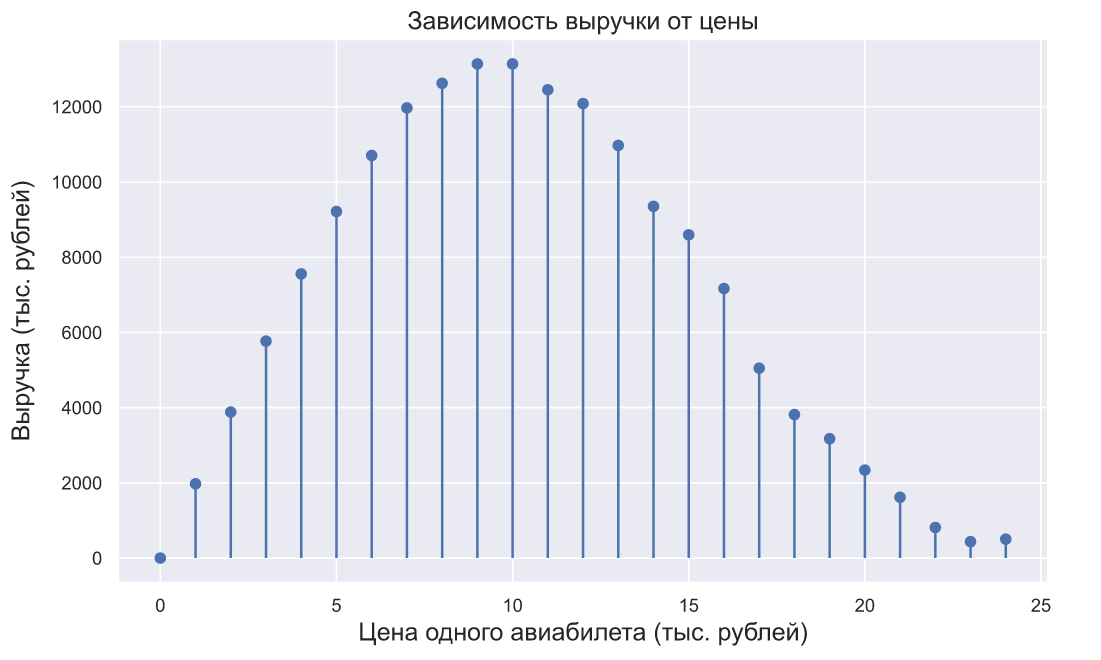
Если бы в авиакомпании взглянули на этот график, то вполне могли бы решить, что оптимальная цена авиабилетов составляет 10 тысяч рублей.
Но что если бы в авиакомпании изначально знали, о том что спрос на билеты распределен как
где
Давайте изобразим это на графике:
Python
x = np.r_[0: 25]
y = norm.sf(x, mu, sigma)
plt.plot(x, y, c='r', label=r'$P(X \geqslant p_{i})$')
plt.plot(x, x*y, 'bo', lw=3, label=r'$P(X \geqslant p_{i}) \times d_{i}$')
plt.vlines(x, 0, x*y)
plt.xlabel('Цена одного билета (тыс. рублей)', fontsize=15)
plt.legend();
Получается, что кривая спроса может быть получена на основе распределения его плотности вероятности. Тогда возникает вполне закономерный вопрос: почему мы практически всегда пытаемся определить именно кривую спроса, но обделяем вниманием его распределение? На этот вопрос непросто ответить, но можно предположить, что пристальное внимание именно к кривой спроса обусловлено тем, что все началось в эпоху офлайн продаж, а дальше все двигалось по инерции. Например, в обычном магазине вполне возможно посчитать количество посетителей, но нет возможности оценить количество посетителей заинтересованных в каком-то конкретном товаре. В этом случае оценка вероятности продажи одной единицы конкретного товара сильно осложняется. В офлайне гораздо проще и логичнее воспринимать количество проданного товара в некоторый промежуток времени, как случайную величину из Пуассоновского распределения. Можно вообще не вести подсчет посетителей и учитывать только количество единиц проданного товара:
Python
f, ax = plt.subplots()
price = np.array([8, 10, 12, 14, 16])
teoretic_means = 100*norm.sf(price, mu, sigma)
len_periods, n_periods = 20, 5
demand = poisson.rvs(mu=teoretic_means, size=(len_periods, n_periods))
real_means = demand.mean(axis=0)
colors = sns.color_palette('Dark2', n_periods)
for i in range(n_periods):
ax.vlines(np.r_[len_periods*i: len_periods*(i + 1)], 0,
demand.T[i], color=colors[i], label=str(price[i]))
ax.hlines(real_means[i], len_periods*i, len_periods*(i + 1)-1, color='k');
ax.legend(title='Цена (тыс. рублей)')
plt.title('Зависимость количества проданных авиабилетов от цены', fontsize=15)
plt.xlabel('Номер дня', fontsize=15)
plt.ylabel('Количество', fontsize=15, labelpad=10);

На вышеприведенном графике показано как могли бы выглядеть такие продажи авиабилетов при разной цене, где черной линией показано среднее значение продаж в каждом периоде. Именно благодаря средним значениям мы можем построить кривую спроса и определить оптимальную стоимость:
Python
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(10,5))
ax1.plot(price, real_means)
ax1.set(title='"Кривая" спроса', xlabel='Стоимость', ylabel='Среднее количество')
ax2.plot(price, price*real_means)
ax2.set(title='Средняя выручка', xlabel='Стоимость', ylabel='Объем выручки');

Получается, что информация о продажах в офлайне позволяет оценивать только кривую спроса и ее недостаточно для того чтобы оценить его распределение. Но что если продажи переместятся в онлайн и теперь для того, что бы узнать стоимость некоторого товара, допустим, того же авиабилета и, уж тем более, приобрести его, придется зайти на отдельную страничку интернет-магазина (да, для авиабилета уже так происходит, но может не происходит для других товаров или услуг: к примеру, если мы говорим о b2b логистике)? Появится ли у нас информация, которой будет достаточно для оценки распределения?
Допустим страницу с авиабилетом по направлению «A-B» посетили 20 человек, если спрос распределен как
X = norm.rvs(mu, sigma, 20)
X
array([18.79350012, 17.82463618, 19.93989386, 2.45863418, 13.00361375,
12.45140662, 9.19133558, 13.62229695, 10.39279135, 12.80996134,
29.00937781, 13.58565382, 13.79565799, 16.10609668, 12.90322265,
6.50983662, 3.76644135, 11.85354469, 10.65444486, 2.18198959])
Если бы существовал какой-то волшебный способ получить такую выборку, то, даже несмотря на ее крошечный объем, можно все равно получить более-менее правдоподобные оценки параметров распределения:
print(f'mu = {X.mean():.3}, sigma = {X.std(ddof=1):.3}')
mu = 12.5, sigma = 6.29
Но волшебства не существует, и все что нам остается это устанавливать и менять цену, наблюдая сколько посетителей совершит или не совершит покупку. Если каждый из 20 смоделированных выше посетителей увидит, что билет стоит 11 тысяч рублей, то единственное, что мы узнаем в итоге, это то, что:
print(f'{sum(X >= 11)} посетителей из 20 совершили покупку.')
13 посетителей из 20 совершили покупку.
Кажется что цена — это просто цена, тем не менее, можно задать простой вопрос: чем цена на товар в офлайне отличается от той же самой цены в онлайне? Пусть случайная величина
где
После того как мы получили оценку вероятности продажи одной единицы товара, цена перестала быть просто ценой, ведь теперь 0.45-квантиль величины
Значение квантиля показывает нам с какой вероятность значение
Python
N = 1000
p_est = np.cumsum(norm.rvs(mu, sigma, N) > 11)/np.r_[1 : N + 1]
plt.plot(p_est)
plt.hlines(norm.sf(11, mu, sigma), 0, N, color='k', ls='--')
plt.title('Изменение оценок квантильного уровня')
plt.xlabel('Количество посетителей')
plt.ylabel('Уровень');
В пределе значение
Величина
Если предположить, что
а это значит, что на основе
Допустим мы установили стоимость авиабилета в 7 тысяч рублей, представим, что в течение для его купили 50 посетителей из 55, пусть
и
тогда мы можем оценить вероятность продажи 50-и авиабилетов 55-и посетителям для разных значений
Изобразим данные оценки в виде тепловой карты:
Python
mu_est = np.linspace(2, 22, 21)
sigma_est = np.linspace(1, 11, 21)
MU, SIGMA = np.meshgrid(mu_est, sigma_est)
price, u, z = 7, 50, 55
p = norm.sf(price, loc = MU, scale=SIGMA)
P1 = binom.pmf(u, z, p)
sns.heatmap(P1, xticklabels = mu_est, yticklabels=sigma_est,
square=True, linewidths=.5)
plt.title('Вероятности продажи 50 авиабилетов 55-и посетителям\n \
по 7 тыс. рублей за штуку')
plt.xlabel('$\widehat{\mu}$', fontsize=20)
plt.ylabel('$\widehat{\sigma}$', rotation=0, fontsize=20, labelpad=15);
Если в следующий день установить стоимость в 14 тысяч рублей и представить, что было продано 16 билетов 34-м посетителям, то тепловая карта будет выглядеть так:
Python
mu_est = np.linspace(2, 22, 21)
sigma_est = np.linspace(1, 11, 21)
MU, SIGMA = np.meshgrid(mu_est, sigma_est)
price, u, z = 14, 16, 34
p = norm.sf(price, loc = MU, scale=SIGMA)
P2 = binom.pmf(u, z, p)
sns.heatmap(P2, xticklabels = mu_est, yticklabels=sigma_est,
square=True, linewidths=.5)
plt.title('Вероятности продажи 16 авиабилетов 34-м посетителям\n \
по 14 тыс. рублей за штуку')
plt.xlabel('$\widehat{\mu}$', fontsize=20)
plt.ylabel('$\widehat{\sigma}$', rotation=0, fontsize=20, labelpad=15);
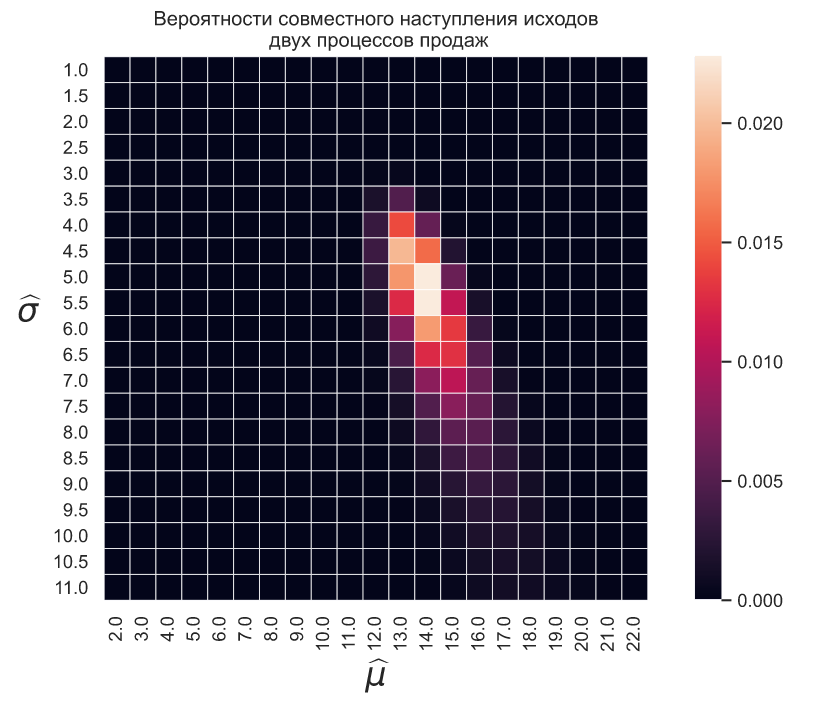
Имея всего два квантиля мы можем оценить вероятность совместного наступления двух исходов как простое произведение вероятностей их отдельного наступления:
Python
sns.heatmap(P1*P2, xticklabels = mu_est, yticklabels=sigma_est, square=True, linewidths=.5)
plt.title('Вероятности совместного наступления исходов\n \
двух процессов продаж')
plt.xlabel('$\widehat{\mu}$', fontsize=20)
plt.ylabel('$\widehat{\sigma}$', rotation=0, fontsize=20, labelpad=15);
При наличии некоторого количества квантилей мы можем найти наилучшие оценки
Например, двух вышеприведенных квантилей достаточно чтобы получить первые оценки параметров распределения спроса, а значит — приступить к процессу максимизации выручки:
Python
# функция для вычисления оптимальной цены
# на основе оценок параметров распределения спроса
def optim_price(prices, mu_est, sigma_est):
return prices[np.argmax(norm.sf(prices, mu_est, sigma_est)*prices)]
# функция для вычисления оценок параметров
# спроса и их максимальных значений
def param_est(used_prices, u, n):
used_prices = used_prices.reshape(used_prices.size, 1, 1)
u = u.reshape(u.size, 1, 1)
n = n.reshape(n.size, 1, 1)
mu_est = np.linspace(2, 22, 21)
sigma_est = np.linspace(1, 11, 21)
MU, SIGMA = np.meshgrid(mu_est, sigma_est)
MU = np.expand_dims(MU, axis=0)
SIGMA = np.expand_dims(SIGMA, axis=0)
p = norm.sf(used_prices, loc = MU, scale=SIGMA)
p_est = np.prod(binom.pmf(u, n, p), axis=0)
idx = divmod(np.argmax(p_est), 21)
mu_opt = mu_est[idx[1]]
sigma_opt = sigma_est[idx[0]]
return p_est, mu_opt, sigma_opt
# Создаем список возможных цен:
prices = np.linspace(6, 18, 25)
# Выбираем две неравные друг другу цены, которые на наш
# взгляд являются самыми перспективными для исследований,
# или выбираем их случайно, если таких представлений нет:
used_prices = np.array([7, 14])
# моделируем (в реальности - считаем) количество посетителей:
n = np.array([55, 32])
# моделируем (в реальности - считаем) количество покупателей:
u = np.array([50, 16])
# На основе двух полученных квантилей, вычисляем наилучшие
# оценки параметров распределения спроса:
P_map, mu_est, sigma_est = param_est(used_prices, u, n)
# Сохраняем все значения для визуализации:
P_maps = [P_map]
for i in range(30):
# На основе имеющихся оценок параметров распределения спроса
# вычисляем оптимальную стоимость товара:
used_prices = np.append(used_prices, optim_price(prices, mu_est, sigma_est))
# моделируем (в реальности - считаем) количество посетителей и
# покупателей:
n = np.append(n, np.random.randint(20, 70))
u = np.append(u, np.sum(norm.rvs(12, 5, n[-1]) > used_prices[-1]))
# Используем все данные для вычисления новых значений
# параметров распределения спроса:
P_map, mu_est, sigma_est = param_est(used_prices, u, n)
P_maps.append(P_map)
import matplotlib.animation as animation
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
fig.set_figwidth(16)
fig.set_figheight(8)
ax2 = fig.add_subplot(122, projection='3d')
ax1 = fig.add_subplot(121)
mu_est = np.linspace(2, 22, 21)
sigma_est = np.linspace(1, 11, 21)
MU, SIGMA = np.meshgrid(mu_est, sigma_est)
def animate(i):
fig.suptitle('Процесс сходимости оценок параметров\nраспределения спроса',
fontsize = 20, y = 0.95)
ax1 = sns.heatmap(P_maps[i], cbar=False, xticklabels = mu_est,
yticklabels=sigma_est, square=True)
ax1.set_xlabel('$\widehat{\mu}$', fontsize=20)
ax1.set_ylabel('$\widehat{\sigma}$', rotation=0, fontsize=20, labelpad=15)
ax2.clear()
ax2.plot_surface(MU, SIGMA, P_maps[i], cmap='Wistia', linewidth=1, edgecolor='0.3')
ax2.set_xlabel('$\widehat{\mu}$', fontsize=15)
ax2.set_ylabel('$\widehat{\sigma}$', fontsize=15)
ax2.set_xticks(mu_est[::2])
ax2.set_zticks([])
return ax1
anim = animation.FuncAnimation(fig,
animate,
frames=np.arange(0, len(P_maps)),
interval = 10,
repeat = False)
anim.save('Асимптотическая сходимость.gif',
writer='imagemagick',
fps=8)

Мы можем повторить данный эксперимент 100 раз и взглянуть на динамику усредненных значений:
Python
qa_proceeds = []
prices_data = []
all_visitors = []
prices = np.linspace(6, 18, 25)
for i in range(100):
used_prices = np.random.choice(prices, 2, replace=False)
# генерируем количество посетителей
n = np.random.randint(20, 70, 2)
# генерируем количество покупателей
u = np.array([np.sum(norm.rvs(12, 5, n[i]) > used_prices[i]) for i in range(len(n))])
mu_est, sigma_est = param_est(used_prices, u, n)[1:]
for j in range(20):
used_prices = np.append(used_prices, optim_price(prices, mu_est, sigma_est))
n = np.append(n, np.random.randint(20, 70))
u = np.append(u, np.sum(norm.rvs(12, 5, n[-1]) > used_prices[-1]))
mu_est, sigma_est = param_est(used_prices, u, n)[1:]
prices_data.append(used_prices)
qa_proceeds.append(np.sum(used_prices * u))
all_visitors.append(np.sum(n))
qa_prices_data = pd.concat([pd.Series(i, index=range(len(i))) for i in prices_data])
sns.lineplot(data=qa_prices_data, ci='sd')
plt.hlines(optim_price(prices, 12, 5), 0, len(prices_data[0]) - 1, color='r',
label='Оптимальная стоимость авиабилета')
plt.yticks(prices[::2])
plt.title('Процесс поиска оптимальной цены на основе квантильного анализа')
plt.xlabel('Количество изменений цены')
plt.ylabel('Стоимость одного авиабилета (тыс. рублей)')
plt.legend();
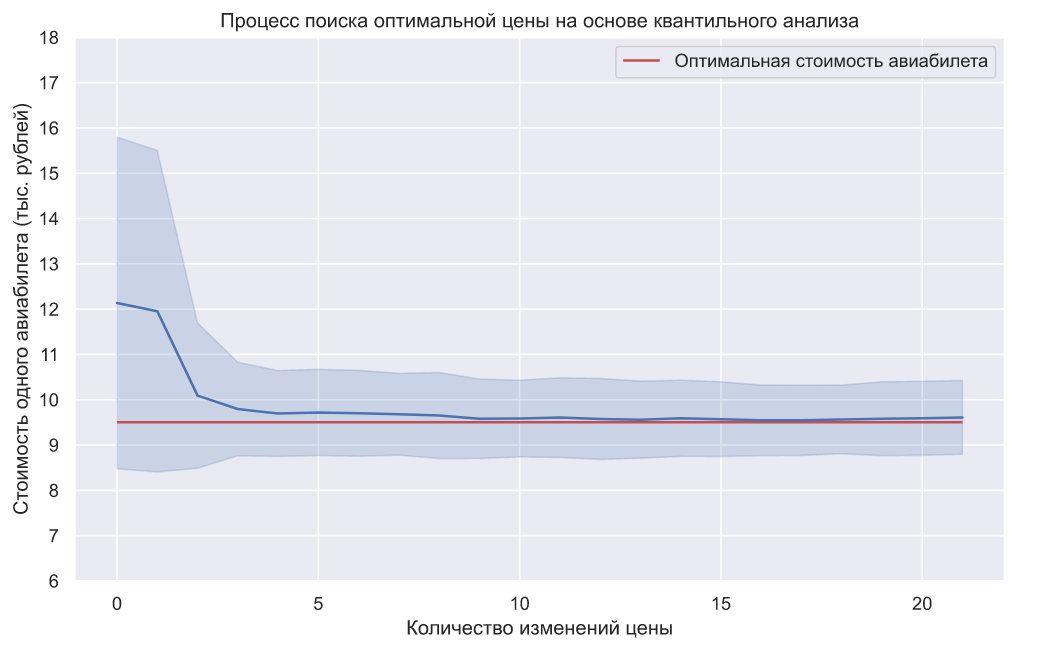
На графике показано среднее значение цены и ее стандартное отклонение. Взглянем на объем выручки в каждом эксперименте:
Python
plt.plot(qa_proceeds)
qa_mean_proc = np.mean(qa_proceeds)
plt.hlines(qa_mean_proc, 0, len(qa_proceeds), color='r',
label=f'Средняя выручка ({int(qa_mean_proc)} тыс. рублей)')
plt.title('Объем выручки в каждом эксперименте')
plt.xlabel('Номер эксперимента')
plt.ylabel('Объем выручки (тыс. рублей)')
plt.legend();
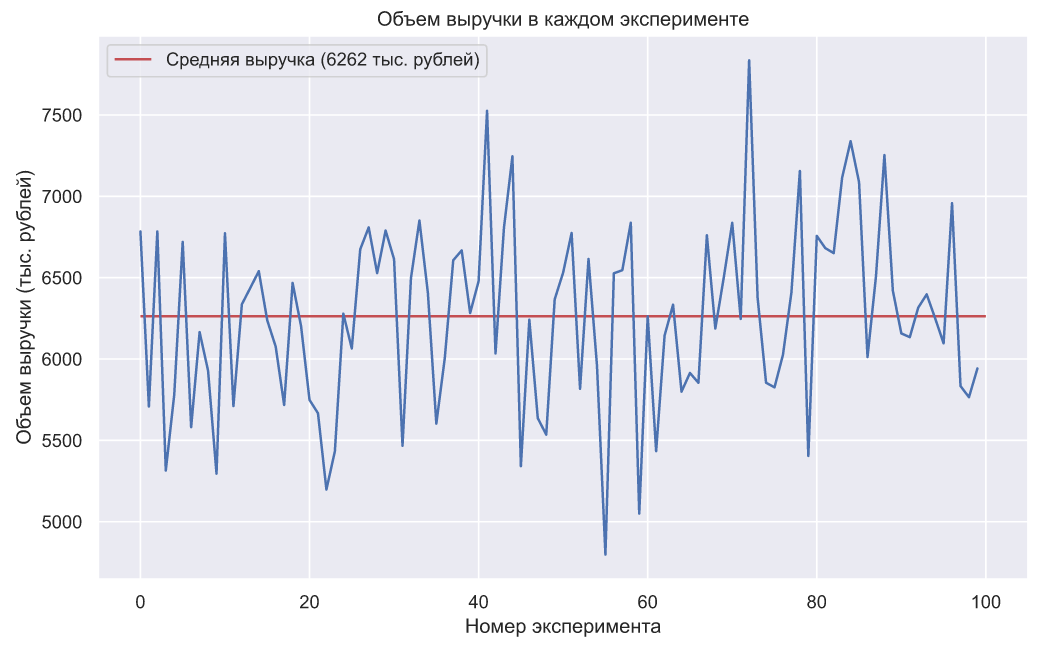
Теперь для сравнения попробуем найти оптимальную стоимость с помощью алгоритма сэмплирования Томпсона (TS). Что бы провести более-менее корректное сравнение, выясним сколько в среднем посетителей участвовало в одном эксперименте на основе квантильного анализа:
np.mean(all_visitors)
985.01
Округлим это значение до 1000 и точно так же повторим эксперимент 100 раз:
Python
def thompson_sampling(a,b):
samples = beta.rvs(a=a+1, b=b+1)
return np.argmax(samples)
n = len(prices)
ts_prices_data = []
ts_proceeds = []
for i in range(100):
# Количество нажатий на рычаг, в нашем случае
# количество использований определенной цены
count = np.zeros(n)
# Сумма наград для каждой руки (количество
# проданного товара по данной цене)
sum_rewards = np.zeros(n)
# Средняя награда от рычага (оценка вероятности
# продажи одной единицы товара)
Q = np.zeros(n)
# Инициализируем значения alpha и beta
a = np.ones(n)
b = np.ones(n)
price = []
proceeds = []
for j in range(1000):
# Выбираем руку с применением выборки Томпсона
arm = thompson_sampling(a, b)
count[arm] += 1
price.append(prices[arm])
# Моделируем посетителя
reward = bernoulli.rvs(norm.sf(prices[arm], 12, 5))
# если reward = 1, значит совершена покупка
if reward == 1:
sum_rewards[arm] += 1
proceeds.append(prices[arm])
# вычисляем вероятность продажи одной единицы товара
Q[arm] = sum_rewards[arm] / count[arm]
# Если выручка по данной цене является максимальной, то:
if arm == np.argmax(prices*Q):
a[arm] += 1 # увеличиваем alpha
else:
b[arm] += 1 # если нет, то увеличиваем beta
ts_prices_data.append(price)
ts_proceeds.append(sum(proceeds))
ts_prices_data = pd.concat([pd.Series(i, index=range(len(i))) for i in ts_prices_data])
sns.lineplot(data=ts_prices_data, ci='sd')
plt.hlines(optim_price(prices, 12, 5), 0, 1000, color='r',
label='Оптимальная стоимость авиабилета')
plt.yticks(prices[::2])
plt.title('Процесс поиска оптимальной цены на основе\n \
алгоритма семплирования Томпсона')
plt.xlabel('Количество изменений цены')
plt.ylabel('Стоимость одного авиабилета (тыс. рублей)')
plt.legend();

И так же взглянем на объем выручки в каждом эксперименте:
Python
plt.plot(ts_proceeds)
ts_mean_proc = np.mean(ts_proceeds)
plt.hlines(ts_mean_proc, 0, len(ts_proceeds), color='r',
label=f'Средняя выручка ({int(ts_mean_proc)} тыс. рублей)')
plt.title('Объем выручки в каждом эксперименте')
plt.xlabel('Номер эксперимента')
plt.ylabel('Объем выручки (тыс. рублей)')
plt.legend();
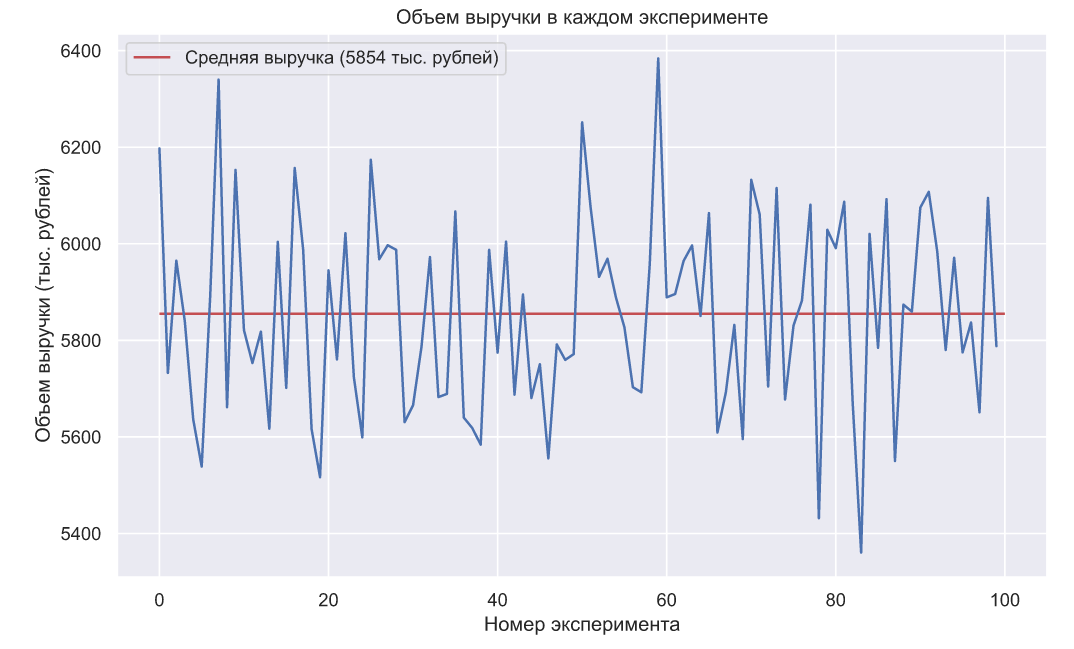
Преимущества квантильного анализа перед TS алгоритмом очевидны:
— более быстрая сходимость;
— гораздо меньшее количество изменений цены;
— незначительное, но все же, увеличение объема выручки.
Разумеется, результаты сравнения выглядят немного подозрительными и для сомнений в их корректности есть основания. Во-первых, алгоритм TS это эвристика, а это значит, что мы можем оптимизировать его множеством самых разных способов. Например, мы можем использовать наши некоторые представления о кривой спроса и перед запуском установить параметры
На первый взгляд, в таком количестве цен для продажи большинства товаров нет никакой логики. Гораздо лучше и логичнее поступить так, как это принято — использовать меньшее количество цен, например:
В этом случае TS алгоритм будет работать просто идеально. Но что если оптимальная цена равна 9.5 тысяч рублей? В случае небольших объемов продаж это не критично, но если объемы продаж велики, то это негативно скажется на прибыли. Основное требование к продаже авиабилетов как раз и заключается в том, что количество проверяемых цен должно быть максимально большим. А что если спрос изменится и оптимальная цена вообще покинет установленный диапазон цен? Это означает, что мы все равно должны как-то учитывать цены за пределами выбранного диапазона, т.е. так или иначе цен становится еще больше. Конечно, вышеприведенные эксперименты предполагали стационарность спроса на авиабилеты, который в действительности является динамическим. Алгоритм TS может быть модифицирован для работы с изменяющимся спросом. Суть модификации заключается в ограничении параметров
Все вышеперечисленные трудности можно преодолеть с разной степенью успеха благодаря множеству модификаций TS алгоритма. Но самая главная проблема заключается в том, что данные о продажах, появляющиеся в ходе его работы абсолютно непригодны для решения задачи глобальной оптимизации. Ведь в действительности, даже имея на руках самый идеальный алгоритм ценообразования, от него не будет абсолютно никакого толка если авиакомпания не выполнит оптимальную расстановку авиапарка по маршрутам. В свою очередь, от алгоритмов ценообразования и расстановки авиапарка также не будет никакой пользы, если авиакомпании не будут иметь согласованных стратегий (для общего эффекта на отрасль в короткие сроки; если же стратегии не согласованы, то рынок бы тоже выровнялся со временем при внедрении алгоритмов хотя бы одной авиакомпанией, но, к сожалению, отрасль является в том или ином виде дотационной во многих странах мира, что сильно ограничивает возможности саморегулирования). А ведь помимо авиакомпаний в системе присутствуют и другие игроки, например, поставщики топлива и аэропорты, чьи действия могут свести на нет даже самую оптимальную стратегию авиакомпаний. Это чрезвычайно сложная система, которая, как это ни странно, существует в основном только за счет кошельков конечных потребителей. Поэтому единственный способ начать оптимизацию всей системы — это начать с ценообразования.
Например, суть расстановки авиапарка заключается в том, что мы должны постоянно принимать управляющие решения о назначении самолетов конкретного типа на конкретные маршруты, для чего необходима информация хотя бы о кривой спроса. Если использовать самую идеальную реализацию TS алгоритма, которая с первых попыток находит оптимальную цену, то окажется что для восстановления кривой спроса просто не окажется нужных данных по другим ценам. Сначала это не кажется проблемой, ведь у нас есть идеальный алгоритм ценообразования, но в этой ситуации алгоритм глобальной оптимизации тоже становится эвристическим, т.е. для того что бы понять, что какому-то самолету не стоит летать по данному направлению, придется понести серьезные убытки. Наличие кривых спроса, наоборот, позволяет без всяких экспериментов сразу менять маршруты и расписания с минимальными убытками.
Квантильный анализ требует установки всего двух исследуемых цен, которые могут выбираться как случайно, так и на основе имеющейся аналитики. Все последующие изменения делаются только на основе уточняющихся оценок параметров распределения спроса. Это означает, что квантильный анализ не является эвристическим и, каким бы ни было количество возможных цен, исследоваться будут только те цены, которые считаются оптимальными на данном этапе. И самое главное, появляющиеся после каждого очередного квантиля оценки, могут быть использованы в многоэтапных задачах стохастической оптимизации. Казалось бы — все круто. Но у квантильного анализа есть один существенный минус — непонятно каким должен быть объем выборки, т.е. непонятно сколько нужно посетителей для того, чтобы оценка квантильного уровня была более-менее статистически значимой. Если использовать для оценки вероятности продажи одной единицы товара
Последовательный статистический анализ Вальда
Первоначальные оценки параметров спроса могут быть как верными так и нет, это значит, что мы можем с первых попыток найти самую оптимальную цену, ну или по крайней мере близкую к ней. Убедиться в оптимальности цены довольно просто, ведь если оценки параметров спроса верны, то вычисленная вероятность продажи одной единицы товара
Выдвинем основную гипотезу
Мы можем принять гипотезу
или принять гипотезу
В случае когда
мы продолжаем торговлю.
Критерий Вальда включает в себя критерий Неймана-Пирсона как частный случай, то есть может обеспечить те же самые уровни ошибок
Python
alpha, beta = 0.05, 0.5
A = np.log((1 - beta)/alpha)
B = np.log(beta/(1 - alpha))
p0, p1 = 0.45, 0.55
# Моделируем выборку для последовательного анализа:
samples_p0 = bernoulli.rvs(p0, size = 100, random_state=42)
# Подсчитываем количество последовательных извлечений
# из выборки:
n = np.r_[1:samples_p0.size + 1]
# подсчитываем количество успешных исходов:
u = samples_p0.cumsum()
z = n - u
stat = u * np.log(p1/p0) + z * np.log((1 - p1)/(1 - p0))
sns.lineplot(x = n, y = stat)
plt.hlines(A, 1, 100, color='g', label='$\ln A$')
plt.hlines(B, 1, 100, color='r', label='$\ln B$')
if np.any(stat > A):
stop_n = (stat < A).argmin()+ 1
else:
if np.any(stat < B):
stop_n = (stat > B).argmin()
plt.vlines(stop_n, -1, 2.5, color='0.3', lw=2, alpha=0.5)
plt.vlines(70, -1, 2.5, color='m', lw=6, alpha=0.5)
plt.xlabel('Количество испытаний')
plt.ylabel('Статистика')
plt.title('Процесс последовательного анализа Вальда')
plt.legend();
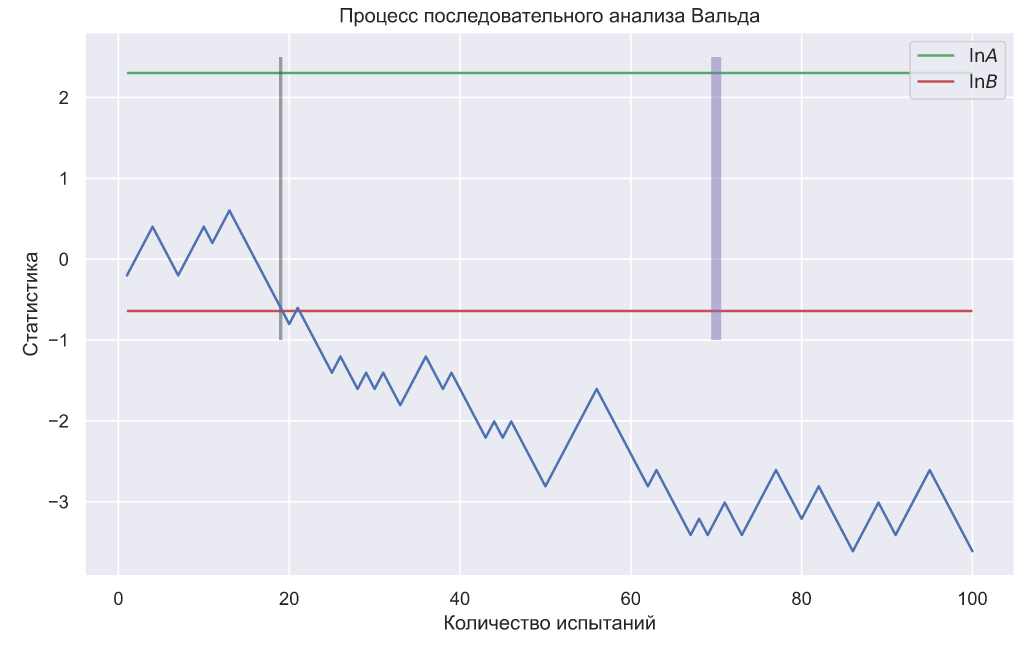
Фиолетовой линией обозначен объем выборки, рассчитанный по критерию Неймана-Пирсона, а серой линией обозначено количество испытаний в критерии Вальда. На графике видно, что в этом конкретном случае потребовалось гораздо меньше испытаний, чем для критерия Неймана-Пирсона. Тем не менее иногда количество испытаний может превышать количество, требуемое для критерия Неймана-Пирсона:
Python
plt.hlines(A, 1, 100, color='g', label='$\ln A$')
plt.hlines(B, 1, 100, color='r', label='$\ln B$')
plt.vlines(70, -1, 2.5, color='m', lw=6, alpha=0.5)
for i in range(20):
samples_p0 = bernoulli.rvs(p0, size = 100)
n = np.r_[1:samples_p0.size + 1]
u = samples_p0.cumsum()
z = n - u
stat = u * np.log(p1/p0) + z * np.log((1 - p1)/(1 - p0))
#sns.lineplot(x = n, y = stat, alpha=0.9)
if np.any(stat > A):
stop_n = (stat < A).argmin()+ 1
else:
if np.any(stat < B):
stop_n = (stat > B).argmin()
sns.lineplot(x = n[:stop_n], y = stat[:stop_n], alpha=0.9)
plt.vlines(stop_n, -1, 2.5, color='0.3', lw=2, alpha=0.7)
plt.xlabel('Количество испытаний')
plt.ylabel('Статистика')
plt.title('Процессы последовательного анализа Вальда в 20-и экспериментах')
plt.legend(loc='lower left');
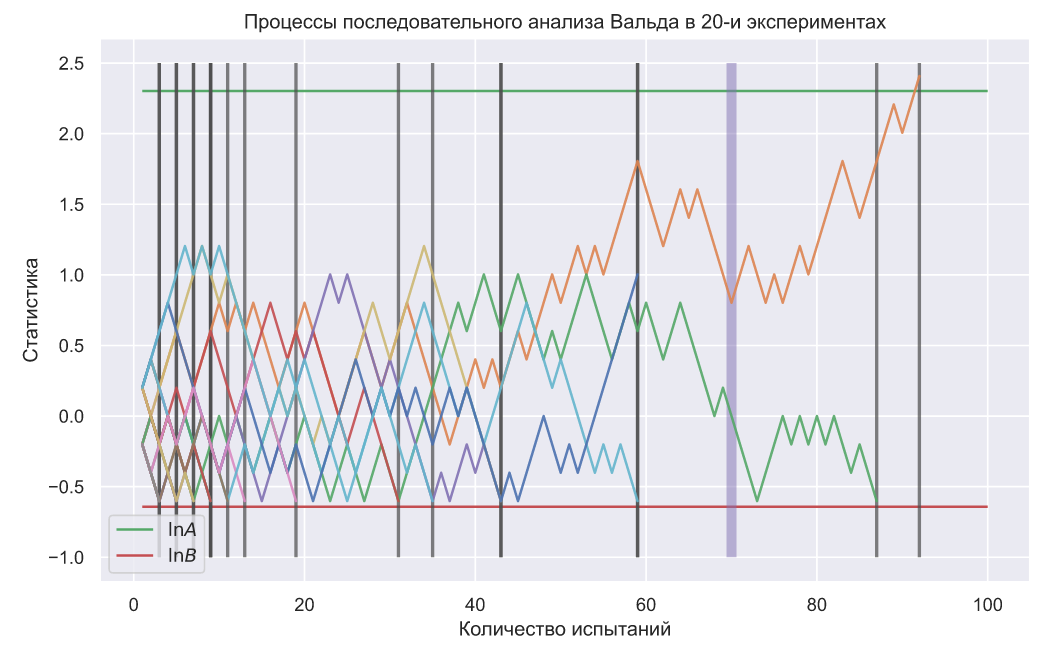
Теперь проверим заданный уровень ошибок для α. Смоделируем 10000 последовательных анализов в предположении, что каждый посетитель может купить одну единицу товара с вероятностью равной 0.45. В этом случае мы должны всегда принимать нулевую гипотезу, но поскольку α=0.05, то критерий Вальда должен ошибаться примерно в 5% случаев:
Python
N = 10000
a, one_m_a = 0, 0
h_test, exper = [], []
for i in range(N):
u, n = 0, 0
stat = (A - B)/2
while B < stat < A:
n += 1
u += bernoulli.rvs(p0)
z = n - u
stat = u * np.log(p1/p0) + z * np.log((1 - p1)/(1 - p0))
if stat > A:
a +=1
h_test.append(0)
if stat < B:
one_m_a += 1
h_test.append(1)
exper.append(n)
plt.text(-0.15, a + 100, fr'$\alpha = ${a/N:.4}', fontsize = 20)
plt.text(1-0.25, one_m_a + 100, fr'$1 - \alpha = ${one_m_a/N:.4}', fontsize = 20)
plt.title(r'Количество ошибок первого рода (верная $H_{0}$ отвергнута)')
sns.countplot(x=h_test)
plt.xticks(ticks = [0,1], labels = [r'$H_{0}$ отвергнута', r'$H_{0}$ принята'])
plt.ylim(0, N + 1000);
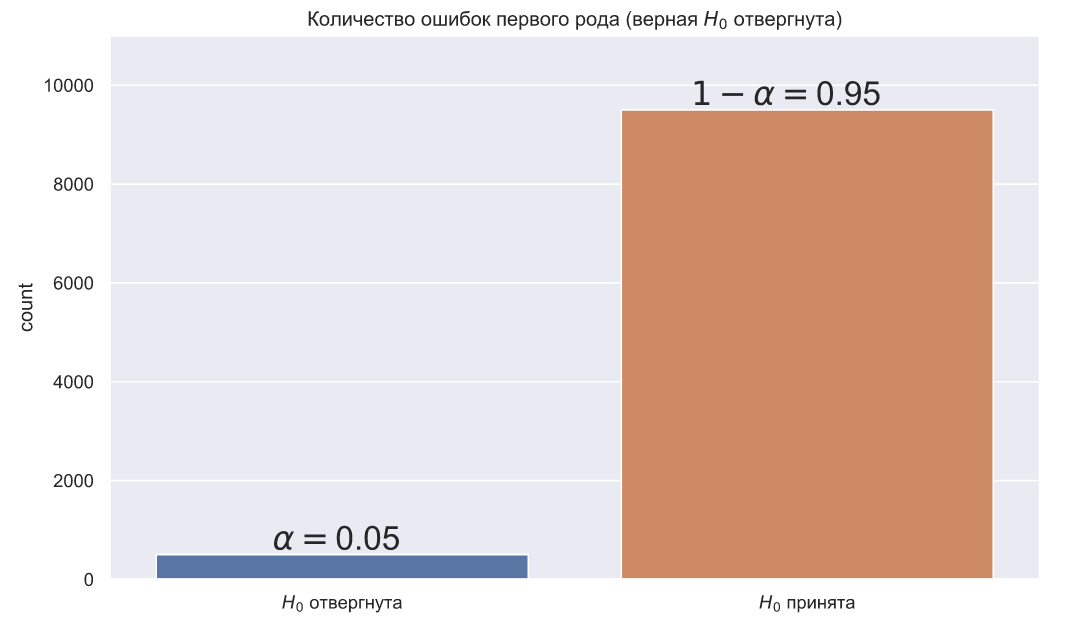
Вообще, в силу дискретной природы некоторых распределений и произвольных вещественных значений
Python
sns.histplot(x=exper, discrete=True)
plt.vlines(np.mean(exper), 0, 900, color='r', label=f'{np.mean(exper):.4}')
plt.title('Распределение количества испытаний в экспериментах')
plt.xlabel('Количество испытаний в одном эксперименте')
plt.ylabel('Количество экспериментов')
plt.legend();
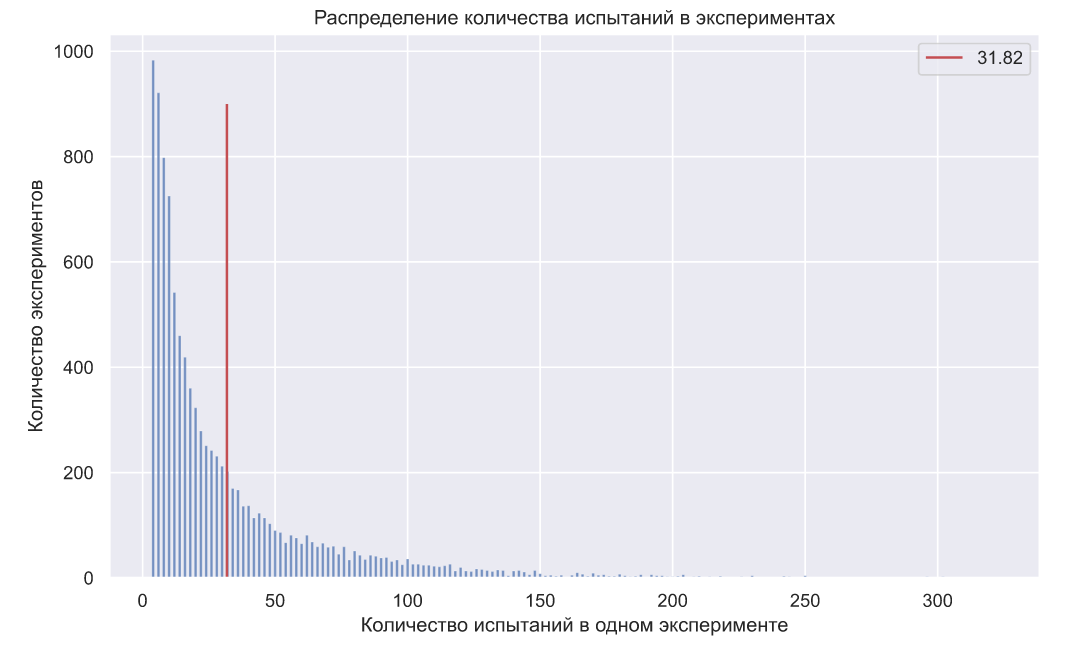
Выполним ту же проверку для ошибок второго рода (
Python
N = 10000
b, one_m_b = 0, 0
h_test, exper = [], []
for i in range(N):
u, n = 0, 0
stat = (A - B)/2
while B < stat < A:
n += 1
u += bernoulli.rvs(p1)
z = n - u
stat = u * np.log(p1/p0) + z * np.log((1 - p1)/(1 - p0))
if stat > A:
b +=1
h_test.append(0)
if stat < B:
one_m_b += 1
h_test.append(1)
exper.append(n)
plt.text(-0.18, b + 100, fr'$1 - \beta = ${b/N:.4}', fontsize = 20)
plt.text(1-0.15, one_m_b + 100, fr'$\beta = ${one_m_b/N:.4}', fontsize = 20)
sns.countplot(x=h_test)
plt.xticks(ticks = [0,1], labels = [r'$H_{0}$ отвергнута', r'$H_{0}$ принята'])
plt.title('Количество ошибок второго рода (неверная $H_{0}$ принята)')
plt.ylim(0, N + 1000);

Полученное значение
Python
sns.histplot(x=exper, discrete=True)
plt.vlines(np.mean(exper), 0, 900, color='r', label=f'{np.mean(exper):.4}')
plt.title('Распределение количества испытаний в экспериментах')
plt.xlabel('Количество испытаний в одном эксперименте')
plt.ylabel('Количество экспериментов')
plt.legend();
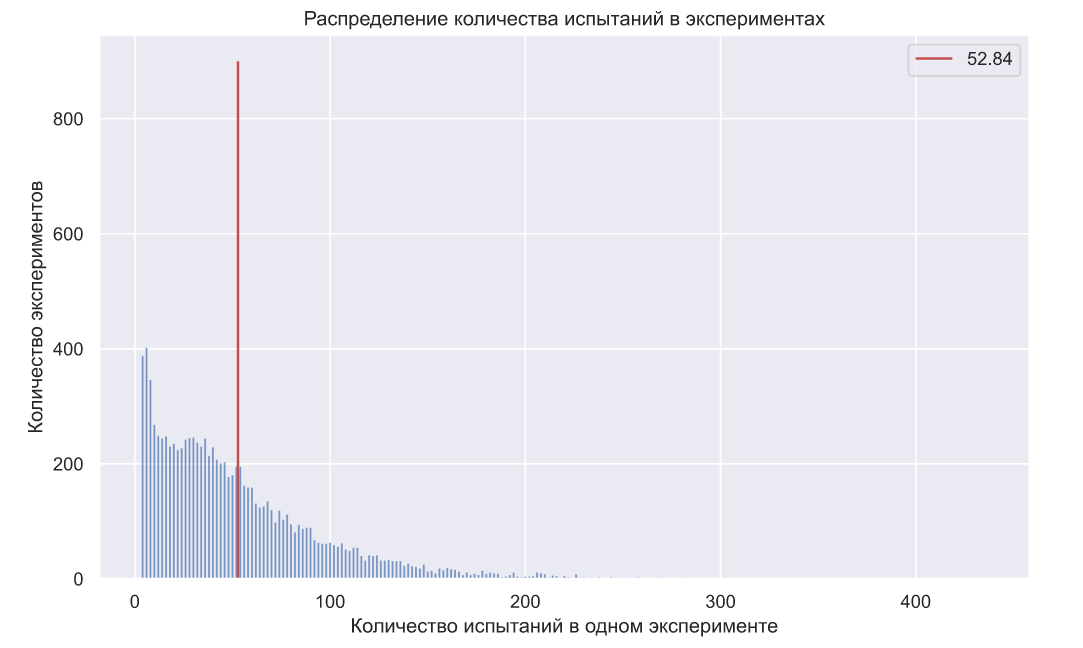
Большим преимуществом критерия Вальда является то, что чем сильнее мы ошибаемся в оценках параметров распределения спроса, тем меньше требуется посетителей для того, чтобы убедиться в этом. Следовательно, мы быстрее вычисляем новые оценки и на их основе определяем новую стоимость товара.
В качестве простой демонстрации того как критерий Вальда может быть использован предположим, что нам необходимо продать какое-то ограниченное количество товара в некоторый фиксированный промежуток времени. Пусть
Для моделирования создадим несколько вспомогательных функций.
Python
# функция определения оптимальной цены по
# оценкам mu и sigma:
def optim_price(q, n, mu_est, sigma_est):
prices = np.linspace(3, 38, 2*(38-3)+1)
p_est = norm.sf(prices, loc=mu_est, scale=sigma_est)
prop = np.clip(n * p_est, a_min = 0, a_max=q)
income = prices * prop
return prices[income.argmax()]
Работает данная функция очень просто: принимает значения имеющихся оценок параметров спроса, вычисляет вероятности продажи одной единицы товара по каждой из возможных цен, а затем выбирает наилучшую из них. Данная функция может определять цену несколько выше, чем та, благодаря которой можно продать весть товар. Например, если у нас есть 10 единиц товара, и по цене 10 у.е мы можем продать все, а по цене 12 у.е. — только 9 единиц, то функция вернет 12 у.е. потому что
# функция для моделирования одного посетителя:
def visitor(price, mu, sigma):
return int(norm.rvs(loc=mu, scale=sigma) > price)
Генерируем одно значение из скрытого распределения спроса и если оно окажется больше установленной цены, то выдаем 1 — товар куплен; в противном случае выдаем 0 — товар не куплен.
Далее, нам понадобится реализация критерия Вальда:
Python
def vald(vis, p_est, alpha=0.05, beta=0.5):
A = np.log((1 - beta)/alpha)
B = np.log(beta/(1 - alpha))
p0 = p_est - 0.05
if p0 <= 0: p0 = 0.01
p1 = p_est + 0.05
if p1 >= 1: p1 = 0.99
ln_p = np.log(p1 / p0)
ln_1_mp = np.log((1 - p1) / (1 - p0))
u = np.sum(vis)
n = len(vis)
z = n - u
test = ln_p * u + ln_1_mp * z
if test <= B:
return -1, p0, p1, test # принимаем p0
if test >= A:
return 1, p0, p1, test # принимаем p1
if B < test < A:
return 0, p0, p1, test # продолжаем эксперимент
В данной функции мы используем имеющуюся оценку вероятности продажи одной единицы товара —
1.
2.
3.
Причем отвечать на эти вопросы мы должны с заранее заданным уровнем ошибок
Далее каждый раз когда мы выходим за пределы
Python
# функция определения параметров нормального спроса
def masp(used_prices, u, n):
used_prices = used_prices.reshape(used_prices.size, 1, 1) # цены
u = u.reshape(u.size, 1, 1) # количество покупок
n = n.reshape(n.size, 1, 1) # количество посетителей
mu = np.arange(15, 26)
sigma = np.arange(1, 12)
MU, SIGMA = np.meshgrid(mu, sigma)
MU = np.expand_dims(MU, axis=0)
SIGMA = np.expand_dims(SIGMA, axis=0)
p = norm.sf(used_prices, loc = MU, scale=SIGMA)
z = np.prod(binom.pmf(u, n, p), axis=0)
i, j = divmod(z.argmax(), 11)
return mu[j], sigma[i]
Прежде чем переходить к моделированию процесса торговли сделаем некоторые уточнения. После установки начальной (самой первой) цены, ее коррекция происходит не на основе оценок параметров спроса, для которых пока просто не существует нужных данных, а в ручном режиме. Изменение происходит на некоторую величину, которая кажется наиболее целесообразной. В эксперименте она меняется на минимально возможное изменение цены (0.5 у.е.).
Еще одно замечание связано с тем, что в алгоритме задается максимально возможное изменение цены. Такая мера кажется целесообразной потому, что колебания относительных частот могут иметь очень сильные отклонения, но из-за таких «флуктуаций» относительной частоты изменение цены может быть просто катастрофически неверным. В эксперименте максимальная дельта цены равна 1.5 у.е.
Что бы провести эксперимент, создадим следующую функцию:
Python
def sales_model(mu, sigma, mu_0, sigma_0, Q, N, alpha=0.05, beta=0.5):
'''
mu, sigma - скрытые, истинные параметры спроса;
mu_0, sigma_0 - первоначальные оценки параметров спроса;
Q - исходное количество товара;
N - среднее количество посетителей в рассматриваемый период времени;
'''
# Список для хранения оценок мат.ожидания
# распределения спроса:
M_star = [mu_0]
# Список для хранения оценок СКО распределения
# спроса:
S_star = [sigma_0]
# Список для хранения посетителей при заданной цене:
Visitors = []
M = [] # количество посетителей во время тестов
MS = [] # количество покупок
S = [] # доход полученный при заданной цене
# Список для хранения цен. Значение начальной цены
# вычисляется в соответствии с нашими первоначальными
# (теоретическими) представлениями о параметрах спроса:
prices = [optim_price(Q, N, M_star[0], S_star[0])]
# Список для хранеия оценок вероятностей:
P_star = [norm.sf(prices[-1], loc=M_star[0], scale=S_star[0])]
# Списки для хранения гипотетических вероятностей и теста Вальда:
P0, P1, T = [], [], []
##################################################################
# Начало продаж выполняемое по нашим теоретическим представлениям:
est_flag = 0
vis = []
while est_flag == 0:
N -= 1
v = visitor(prices[-1], mu, sigma)
if v != 0:
Q -= 1
vis.append(v)
test, P0_i, P1_i, T_i = vald(vis, P_star[-1], alpha=alpha, beta=beta)
P0.append(P0_i)
P1.append(P1_i)
T.append(T_i)
if test != 0:
est_flag = 1
M.append(len(vis))
MS.append(sum(vis))
P_star.append(MS[-1] / M[-1])
# меняем цену в соответствии с значением теста
if test == -1:
prices.append(prices[-1] - 0.5)
if test == 1:
prices.append(prices[-1] + 0.5)
# вычисляем первое значение полученной прибыли:
S.append(MS[-1]*prices[-1])
###############################
# Основной цикл
vis=[]
while (N != 0) and (Q != 0):
N -= 1
v = visitor(prices[-1], mu, sigma)
if v != 0:
Q -= 1
vis.append(v)
test, P0_i, P1_i, T_i = vald(vis, P_star[-1], alpha=alpha, beta=beta)
P0.append(P0_i)
P1.append(P1_i)
T.append(T_i)
if test != 0:
M.append(len(vis))
MS.append(sum(vis))
P_star.append(MS[-1] / M[-1])
Visitors.append(vis)
S.append(MS[-1]*prices[-1])
est_par = masp(np.array(prices), np.array(MS), np.array(M))
M_star.append(est_par[0])
S_star.append(est_par[1])
prices.append(optim_price(Q, N, M_star[-1], S_star[-1]))
if prices[-1] - prices[-2] > 1.5:
prices[-1] = prices[-2] + 1
if prices[-1] - prices[-2] < -1.5:
prices[-1] = prices[-2] - 1
vis = []
if Q == 0 and len(vis) != 0:
Visitors.append(vis)
M.append(len(vis))
MS.append(sum(vis))
S.append(MS[-1]*prices[-1])
return MS, M, S, prices, P_star, M_star, S_star, Visitors, P0, P1, T
Итак, проведем эксперимент исходя из следующих начальных условий: спрос распределен как
MS, M, SS, prices, P_star, M_star, S_star, Visitors, P0, P1, T = sales_model(21, 3, 18, 1, 300, 3000, 0.05, 0.1)
Сначала взглянем на то, как работает последовательный анализ Вальда и как он взаимосвязан с изменением интервала
Python
plt.plot(P0[:200], color='g', label='$p_{0}$', zorder=11)
plt.plot(P1[:200], color='g', ls='--', label='$p_{1}$', zorder=10)
plt.plot(T[:200], color='0.3', label='test')
alpha = 0.05
beta = 0.1
A = np.log((1 - beta)/alpha)
plt.hlines(A, 0, 200, color='b', label='A')
B = np.log(beta/(1 - alpha))
plt.hlines(B, 0, 200, color='r', label='B')
plt.legend();
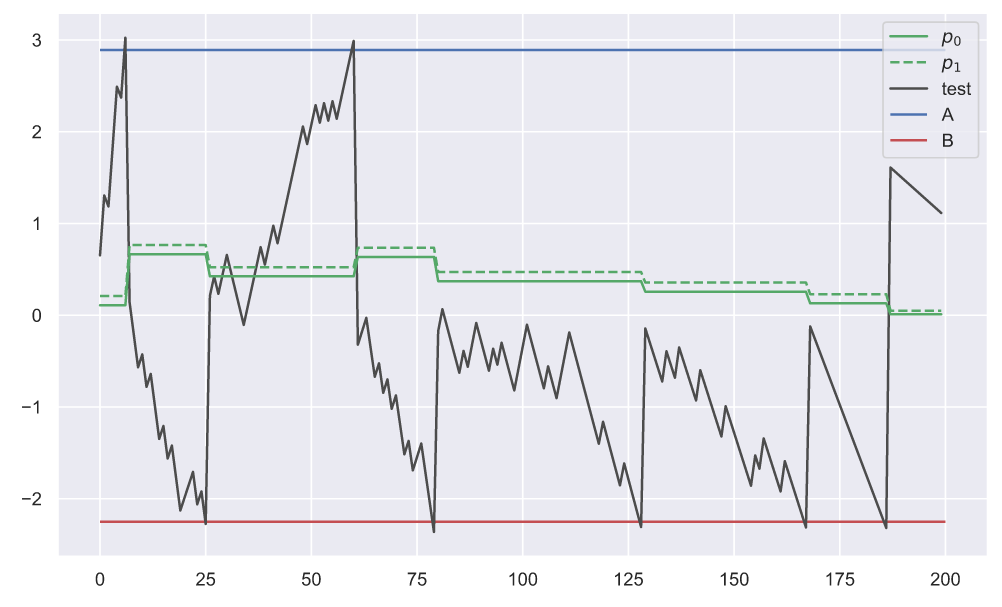
Видно, что границы интервала меняются как только статистика, обозначенная черным цветом, пересекает критические значения (А — снизу, В — сверху).
На графике ниже можно наблюдать быструю сходимость оценок параметров распределения к истинным значениям, даже с учетом того, что наши первоначальные оценки были слишком занижены:
Python
fig, ax = plt.subplots(nrows=1, ncols=2, figsize = (10, 5))
ax[0].plot(M_star)
ax[0].set_title('Оценка мат.ожидания спроса\n(истинное $\mu = 21$)')
ax[0].set_xlabel('Количество оценок вероятностей')
ax[0].set_ylabel('$\mu$', rotation=0, fontsize=20, labelpad=15)
ax[1].plot(S_star)
ax[1].set_title('Оценка отклонения спроса\n(истинное $\sigma = 3$)')
ax[1].set_xlabel('Количество оценок вероятностей')
ax[1].set_ylabel('$\sigma$', rotation=0, fontsize=20, labelpad=15);

Полученные оценки позволяют достичь максимально возможных значений прибыли:
Python
plt.plot(np.cumsum(SS))
plt.hlines(300*optim_price(300, 3000, 21, 3), 0, len(SS),
color='g', label='Максимальная\nсредняя прибыль')
plt.legend(loc='center right')
plt.title('Изменение кумулятивной суммы прибыли')
plt.ylabel('Кумулятивная сумма прибыли')
plt.xlabel('Количество оценок');

При этом цена одной единицы товара не испытывает сильных колебаний:
Python
plt.plot(prices)
plt.hlines(optim_price(300, 3000, 21, 3), 0, len(prices),
color='g', lw=3, alpha=0.5, zorder=100,
label='$Price_{opt}$')
plt.title('Изменение цены 1-й единицы товара')
plt.ylabel('Цена 1-й единицы товара')
plt.xlabel('Количество оценок')
plt.legend(loc='center right');
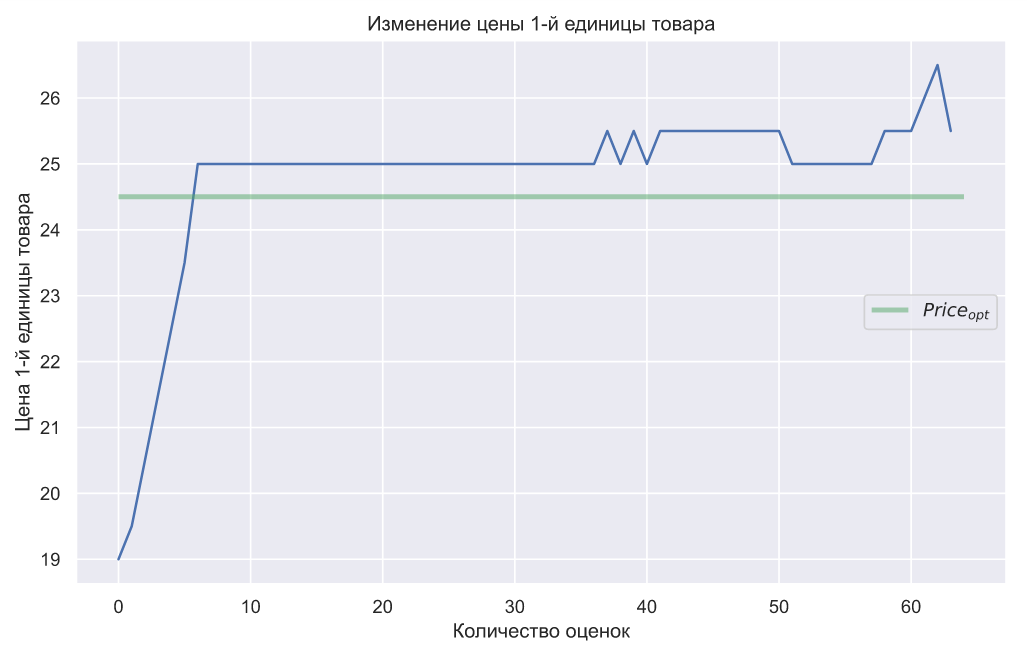
Ну и напоследок, можно видеть, что алгоритм успевает продать весь товар:
Python
plt.plot(np.cumsum(MS))
plt.title('Кумулятивная сумма единиц проданного товара')
plt.ylabel('Кумулятивная сумма')
plt.xlabel('Количество оценок');
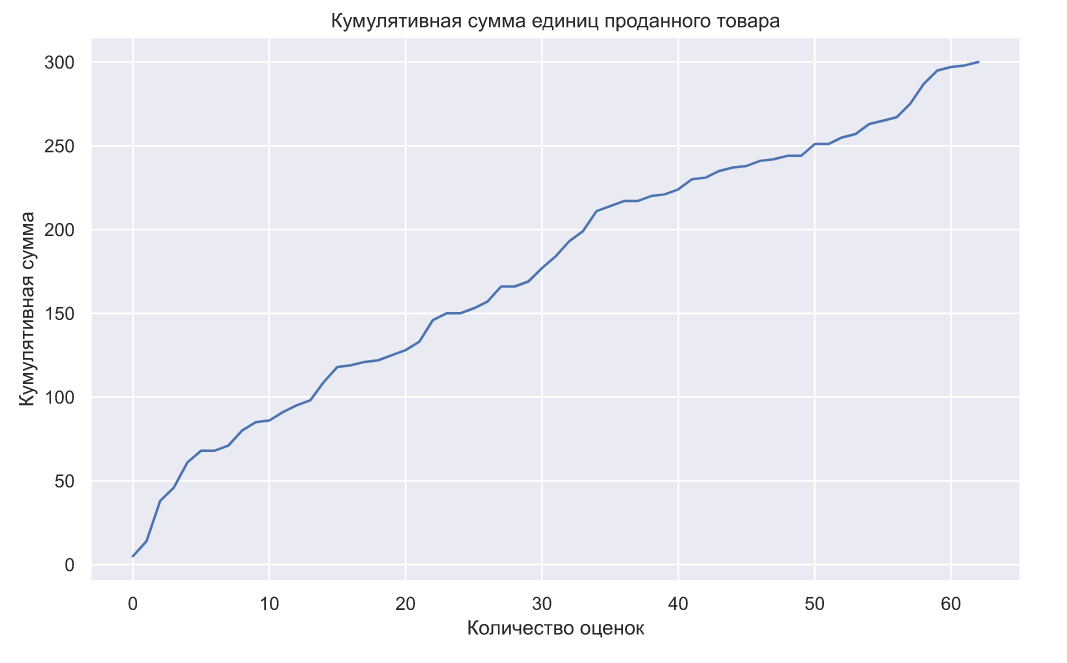
Наши первоначальные оценки параметров распределения спроса были довольно далеки от настоящих, но довольно быстро алгоритм все-таки нашел их правильные значения, и далее все продажи выполнялись по оптимальным ценам. Но самое главное в этом примере то, что благодаря критерию Вальда, мы смогли избавиться от фиксированного объема выборки, более того, благодаря параметрам
В общем, как и в случае алгоритма семплирования Томпсона, представленный алгоритм на основе квантильного и последовательного анализа вовсе не являются универсальным рецептом оптимальных продаж, но принцип его работы на удивление прост и гибок, а это значит, что он может быть легко модифицирован и адаптирован под самые разные задачи. Давайте напоследок именно это и продемонстрируем.
Продажа авиабилетов при динамическом спросе
Стационарный спрос характерен для большого количества товаров, но не меньшее количество товаров характеризуется нестационарным спросом. Так же следует упомянуть, что понятие «оптимальная цена» может сильно меняться в зависимости от контекста. Например, для стационарного спроса оптимальность цены может зависеть от того, чего мы хотим добиться: продавать определенное количество товара, максимизировать валовую прибыль или выручку. Все это может учитываться и при нестационарном спросе, но могут появляться дополнительные требования, например, в ходе продаж может возникнуть срочная потребность в наличных деньгах или срочной распродаже товара. В конечном счете все эти требования к оптимальности цены могут быть учтены в алгоритме. Нас же теперь интересует как модифицировать алгоритм так, чтобы он мог учитывать динамику спроса.
Давайте снова рассмотрим какой-нибудь простой случай: пусть теперь спрос распределен как
Для большей простоты пока предположим, что нам неизвестны только
t = np.array([0, 1, 2, 3, 4])
В каждый из дней мы устанавливали следующие цены:
price = np.array([23, 25, 25, 27, 28])
Количество посетителей в каждый из дней было таким:
m = np.array([40, 31, 35, 48, 50])
Согласно нашей модели, в каждый из дней были следующие значения мат. ожидания нормального распределения:
mu = np.array([20, 21, 22, 23, 24])
Тогда количество проданного товара может быть очень просто смоделировано следующим образом:
ms = np.array([np.sum(norm.rvs(mu[i], 4, m[i]) > price[i]) for i in np.r_[:5]])
ms
array([9, 4, 8, 9, 5])
Теперь перейдем к неизвестным параметрам
e = np.array([0.7, 0.8, 0.9, 1, 1.1, 1.2, 1.3])
А
mu0 = np.array([15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25])
Тогда мы можем предположить, что если
mu_e0 = e[0] * t.reshape(-1, 1) + mu0
mu_e0
array([[15. , 16. , 17. , 18. , 19. , 20. , 21. , 22. , 23. , 24. , 25. ],
[15.7, 16.7, 17.7, 18.7, 19.7, 20.7, 21.7, 22.7, 23.7, 24.7, 25.7],
[16.4, 17.4, 18.4, 19.4, 20.4, 21.4, 22.4, 23.4, 24.4, 25.4, 26.4],
[17.1, 18.1, 19.1, 20.1, 21.1, 22.1, 23.1, 24.1, 25.1, 26.1, 27.1],
[17.8, 18.8, 19.8, 20.8, 21.8, 22.8, 23.8, 24.8, 25.8, 26.8, 27.8]])
Каждый столбец в данном массиве показывает как могло бы меняться мат. ожидание с каждым днем, если бы
Python
ps = norm.sf(price.reshape(5, 1), loc=mu_e0, scale=4)
PS = binom.pmf(ms.reshape(5, 1), m.reshape(5, 1), ps)
sns.heatmap(PS)
xticks_label = [f'{e[0]}t+{i}' for i in mu0]
plt.xticks(np.r_[0.5:11.5], xticks_label, rotation=60)
plt.xlabel('f(t)', fontsize=15)
plt.ylabel('t', fontsize=15, rotation=0, labelpad=10);
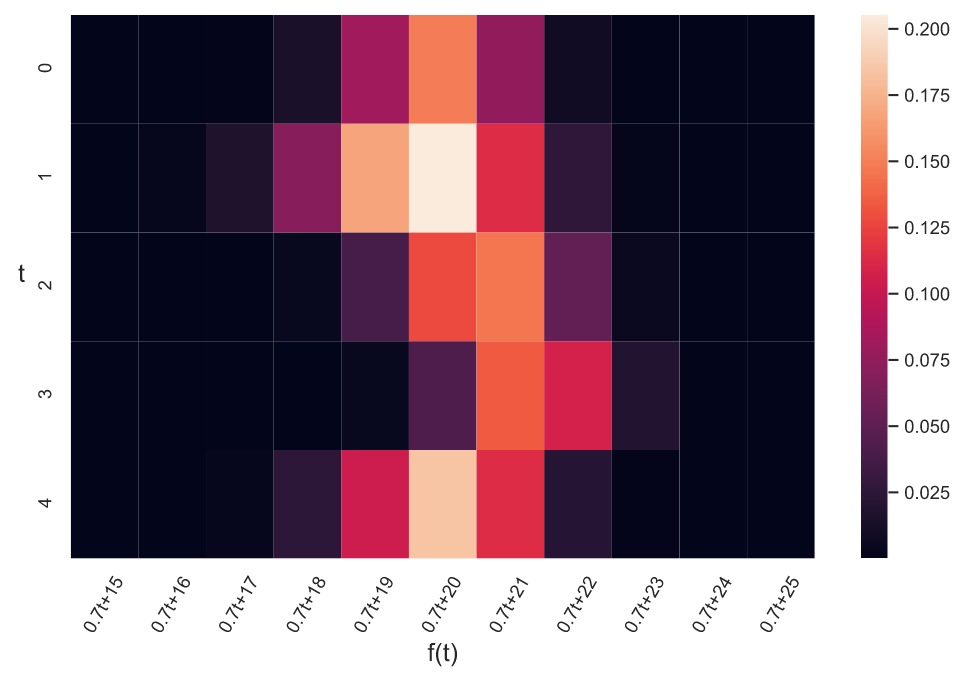
На графике можем наблюдать, что только в столбцах близких к истинному значению
Python
plt.plot(np.sum(np.log(PS), axis=0), marker='o')
plt.xticks(np.r_[0:11], xticks_label, rotation=60);
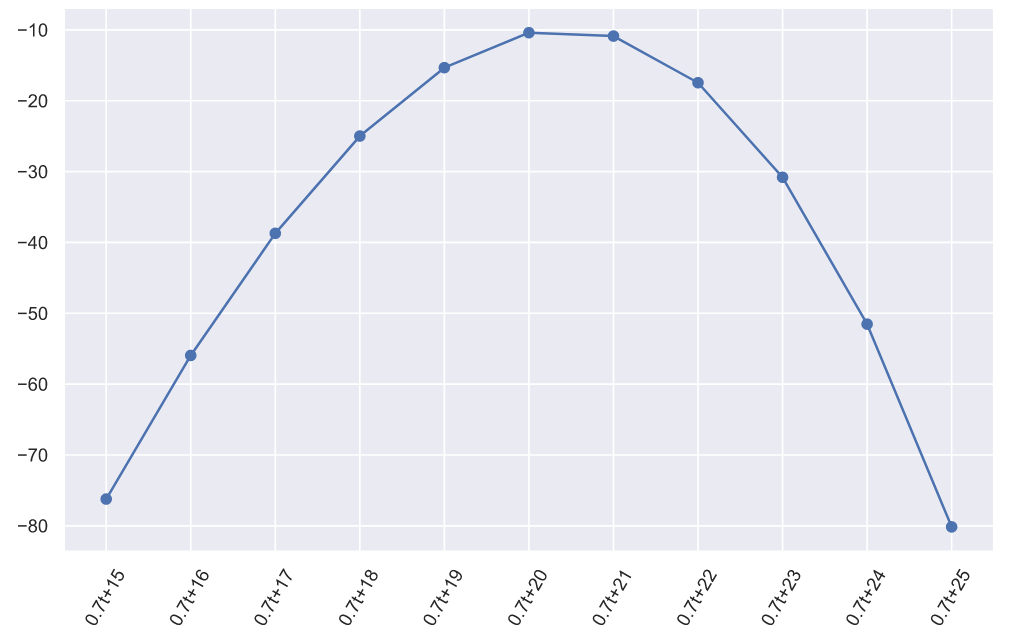
Если построить подобные графики для всех
Python
for i in e:
mu_e0 = i* t.reshape(-1, 1) + mu0
ps = norm.sf(price.reshape(5, 1), loc=mu_e0, scale=4)
PS = binom.pmf(ms.reshape(5, 1), m.reshape(5, 1), ps)
S = np.sum(np.log(PS), axis=0)
plt.plot(S, label=f'$\epsilon$ = {round(i, 1)}')
xticks_label = [fr'$\epsilon$t+{i}' for i in mu0]
plt.xticks(np.r_[0:11], xticks_label, rotation=60)
plt.legend();
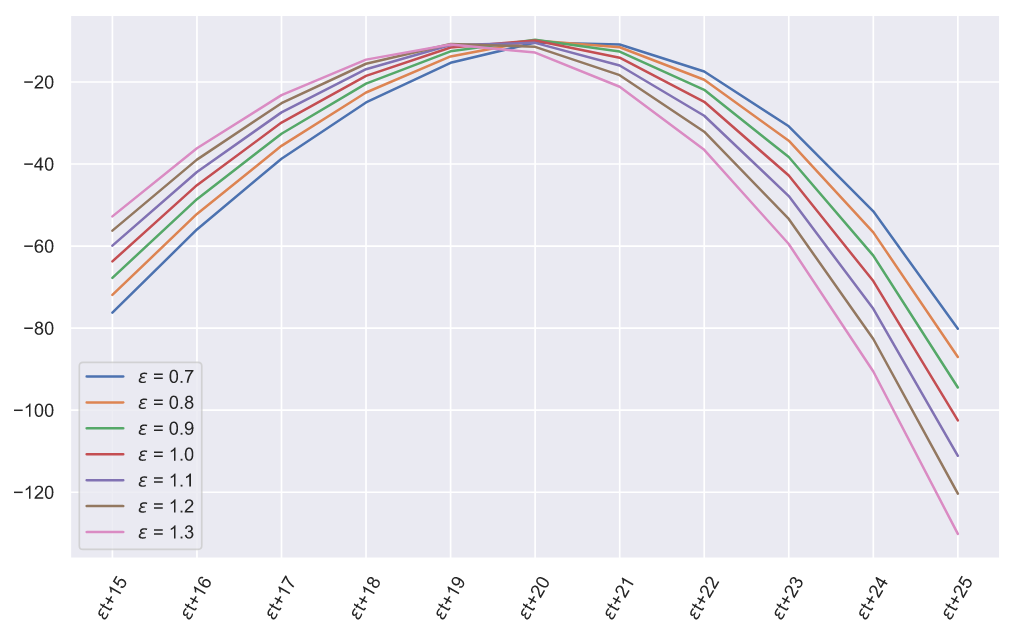
На этом графике, конечно же, невозможно разглядеть максимумы, да и один эксперимент вовсе не показатель сходимости, поэтому проведем больше экспериментов и взглянем на усредненные значения максимумов отдельно:
Python
t = np.r_[0:10]
mu = np.r_[20:30]
res = []
for j in range(5000):
for i in e:
mu_e0 = i*t.reshape(-1, 1) + mu0
price = np.arange(21, 31)
ps = norm.sf(price.reshape(10, 1), loc=mu_e0, scale=4)
m = np.random.randint(25, 70, 10)
ms = np.array([np.sum(norm.rvs(mu[k], 4, m[k]) > price[k]) for k in np.r_[:10]])
PS = binom.pmf(ms.reshape(10, 1), m.reshape(10, 1), ps)
S = np.sum(np.log(PS), axis=0)
res.append([i, np.argmax(S) + 15, S.max()])
res = pd.DataFrame(res, columns=['eps', 'mu', 'val'])
sns.pointplot(x='mu', y='val', hue='eps', dodge=True, errwidth=0, palette='tab10', data=res);

Как видим, наибольшие максимумы соответствуют значениям, которые близки к истинному значению
Python
# функция для моделирования времени обращения посетителей:
def demand_t(T):
D_mu_0, k_3 = 5, 0.65
D_sigma_0, k_4 = 2, 0.18
num_day = np.r_[0: T]
D_mu_t = k_3 * num_day + D_mu_0
D_sigma_t = k_4 * num_day + D_sigma_0
vis_day = norm.rvs(D_mu_t, D_sigma_t).astype(int)
t = np.sort(np.hstack([np.random.randint(i*1440, (i + 1)*1440, j) for i, j in zip(range(T), vis_day)]))
return t
# функция для моделирования одного посетителя:
def visitor(price, t):
money_mu_t = 0.125*t + 9300
money_sigma_t = 0.05*t + 1500
return int(norm.rvs(money_mu_t, money_sigma_t) > price)
time_vis = demand_t(100)
money_vis = norm.rvs(0.125*time_vis + 9300, 0.05*time_vis + 1500)
plt.scatter(time_vis, money_vis, s=10)
plt.xlabel('Время от начала продаж (мин.)')
plt.ylabel('Стоимость билета (руб.)')
plt.title('Модель распределения спроса на авиабилеты');
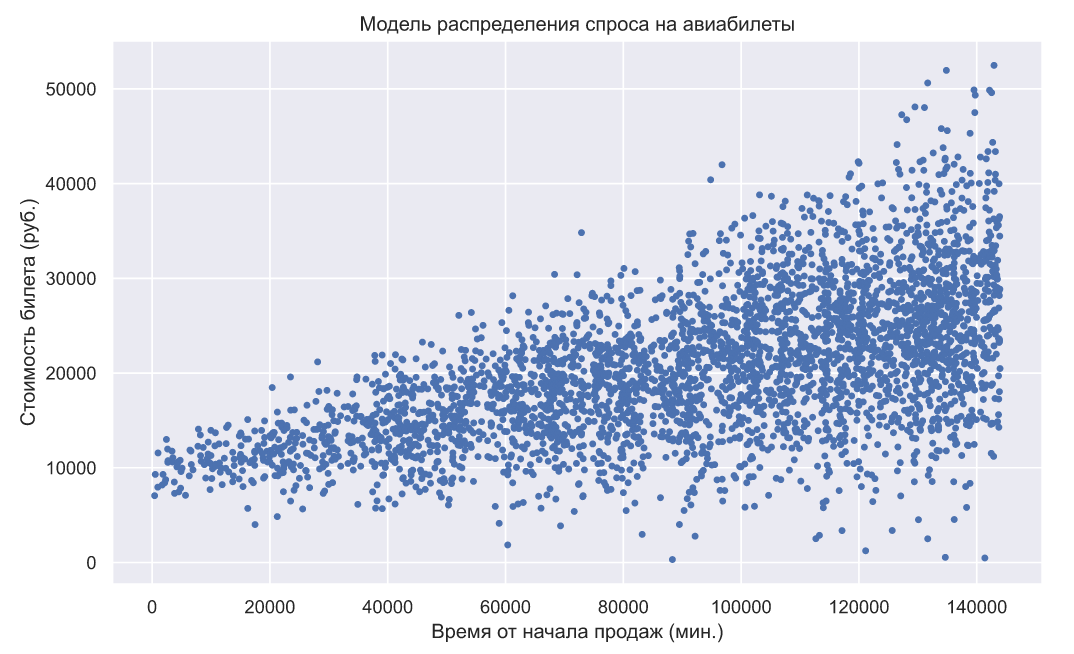
По оси ординат отложена максимальная стоимость билета, выше которой посетитель не может совершить покупку. Допустим, что нам необходимо обеспечить равномерную продажу авиабилетов, т.е. на всем периоде продаж должны иметься доступные для покупки авиабилеты. Данное требование означает, что мы должны изменять цену так, чтобы вероятность продажи одного билета была неизменной на протяжении всего периода продаж. Для этого мы можем создать следующую простую функцию:
def p_prog(q, D_est, mu_est, sigma_est):
p_star = q / D_est
price_star = norm.interval(1 - 2*p_star, loc=mu_est, scale=sigma_est)[1]
return p_star, price_star
Благодаря этой функции мы будем оценивать прогнозируемую вероятность продажи одного билета на ближайшие сутки, а так же выяснять стоимость билета, на основе имеющихся оценок параметров и прогнозируемого количества посетителей. Теперь осталось определить всего две функции: одну для прогнозирования количества посетителей в ближайшие сутки (на основе простой линейной регрессии):
Python
def dem_prog(vis_times):
if vis_times[-1] >= 5*1440:
idx = int(vis_times[-1]/1440)
dem_of_day = [np.sum((vis_times > i*1440) & (vis_times <= (i + 1)*1440)) for i in range(idx)]
t = np.arange(1, idx+1)*1440
reg = np.poly1d(np.polyfit(t, dem_of_day, 1))
D_prog = reg(vis_times[-1] + 1440)
return D_prog
else:
return 10
И еще одну для оценки параметров распределения спроса:
Python
from scipy import optimize
def k_mu_est(T, V, pt):
buy = np.hstack(V)
t = np.hstack(T)
def func(x):
money_mu_t = x[0]*t + x[1]
money_sigma_t = 0.05*t + 1500
p = norm.sf(pt, money_mu_t, money_sigma_t)
z = np.sum(np.log(bernoulli.pmf(buy, p)))
return -z
x0=np.array([K[-1], MU[-1]])
bounds = [(0, 1), (8800, 9800)]
result = optimize.minimize(func,x0=x0,bounds=bounds, method='Powell',
options={'maxiter':100000})
return result['x']
# Количество билетов:
Q = 350
# Генерируем время посещения:
vt = demand_t(100)
# Начальная цена и список для хранения цен в
# момент времени t:
prices, prices_t = [9500], []
# Первоначальные оценки вероятности продажи одного
# билета, и параметров функции мат. ожидания:
P_est, K, MU = [0.35], [0.11], [9100]
# Количество покупок и посетителей при заданной цене:
U, N = [], []
# купил или не купил посетитель билет по заданной цене
# и время обращения:
vis, vis_t = [], []
V, T = [], []
S = []
##################################################################
# Начало продаж выполняемое по нашим теоретическим представлениям:
est_flag = 0
i = 0
while est_flag == 0:
vis_t.append(vt[i])
prices_t.append(prices[-1])
vis.append(visitor(prices[-1], vt[i]))
if vis[-1] == 1:
Q -= 1
test = vald(vis, P_est[-1])[0]
if test != 0:
est_flag = 1
U.append(sum(vis))
N.append(len(vis))
V.append(vis)
T.append(vis_t)
P_est.append(U[-1]/N[-1])
S.append(U[-1]*prices[-1])
# меняем цену в соответствии с значением теста
if test == -1:
prices.append(prices[-1] - 150)
if test == 1:
prices.append(prices[-1] + 150)
i += 1
##################################################################
# Основной цикл:
vis = []
vis_t = []
for i in range(i, len(vt)):
vis_t.append(vt[i])
prices_t.append(prices[-1])
vis.append(visitor(prices[-1], vt[i]))
if vis[-1] == 1:
Q -= 1
test = vald(vis, P_est[-1])[0]
if test != 0:
U.append(sum(vis))
N.append(len(vis))
S.append(U[-1]*prices[-1])
V.append(vis)
T.append(vis_t)
k_est, mu_est = k_mu_est(T, V, prices_t)
K.append(k_est)
MU.append(mu_est)
mu_prog = K[-1]*(vis_t[-1]+1440) + MU[-1]
sigma_prog = 0.05*(vis_t[-1]+1440) + 1500
D = dem_prog(vt[:i])
q = Q/(100-(vis_t[-1])/1440)
p_est, price = p_prog(q, D, mu_prog, sigma_prog)
P_est.append(p_est)
if abs(price - prices[-1]) <= 200:
prices.append(prices[-1])
else:
prices.append(price)
vis = []
vis_t = []
if Q == 0:
if len(vis) != 0:
U.append(sum(vis))
N.append(len(vis))
V.append(vis)
T.append(vis_t)
S.append(U[-1]*prices[-1])
break
Взглянем как менялись выручка, стоимость билета и количество проданных билетов:
Python
f, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(12, 3))
ax1.plot(np.cumsum(np.array(SS)/1000))
ax1.set_title('Выручка (млн. руб.)')
ax2.plot(prices)
ax2.set_title('Цена (тыс. руб.)')
ax3.plot(np.cumsum(U))
ax3.set_title('Проданных билетов')
ax3.set_yticks(np.r_[0:400:50]);
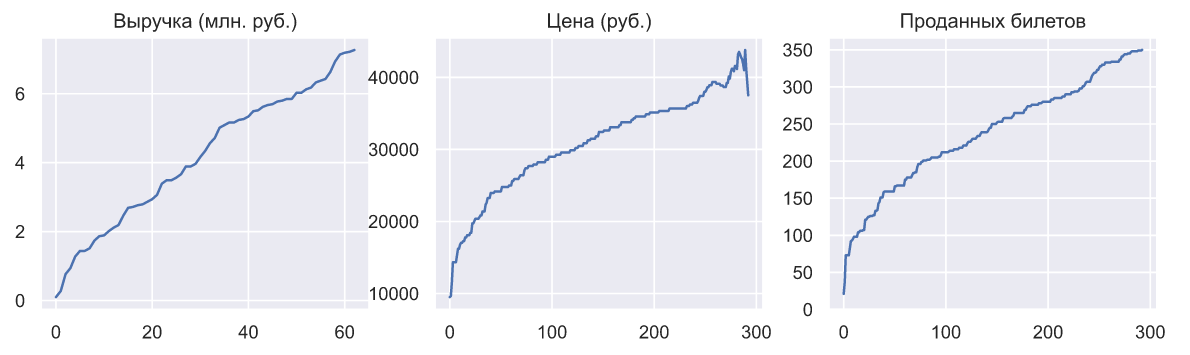
Это неплохой результат, который, кстати, был обеспечен не такими уж точными оценками параметров:
Python
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4))
ax1.plot(MU)
ax1.set_title(r'Изменение оценок $\mu_{0}$')
ax2.plot(K)
ax2.set_title(r'Изменение оценок $k_{1}$');
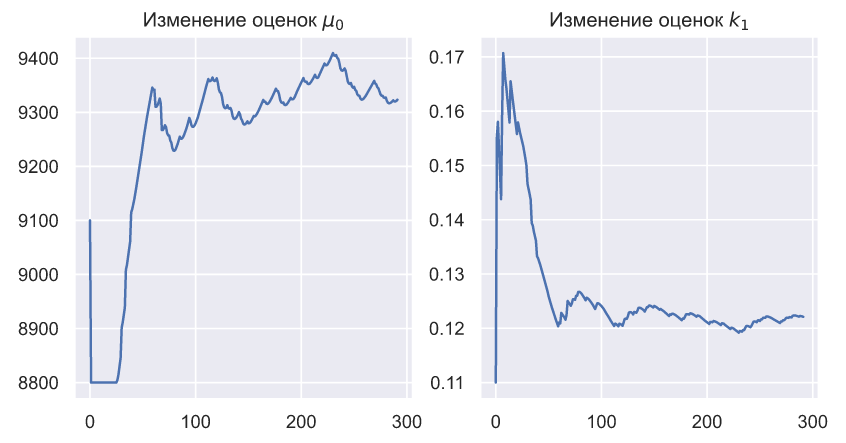
Можно еще раз задаться вопросом: зачем вообще нужен критерий Вальда? Ведь если выполнять квантильный анализ после каждого 25-го посетителя, то можно добиться практически тех же самых результатов:
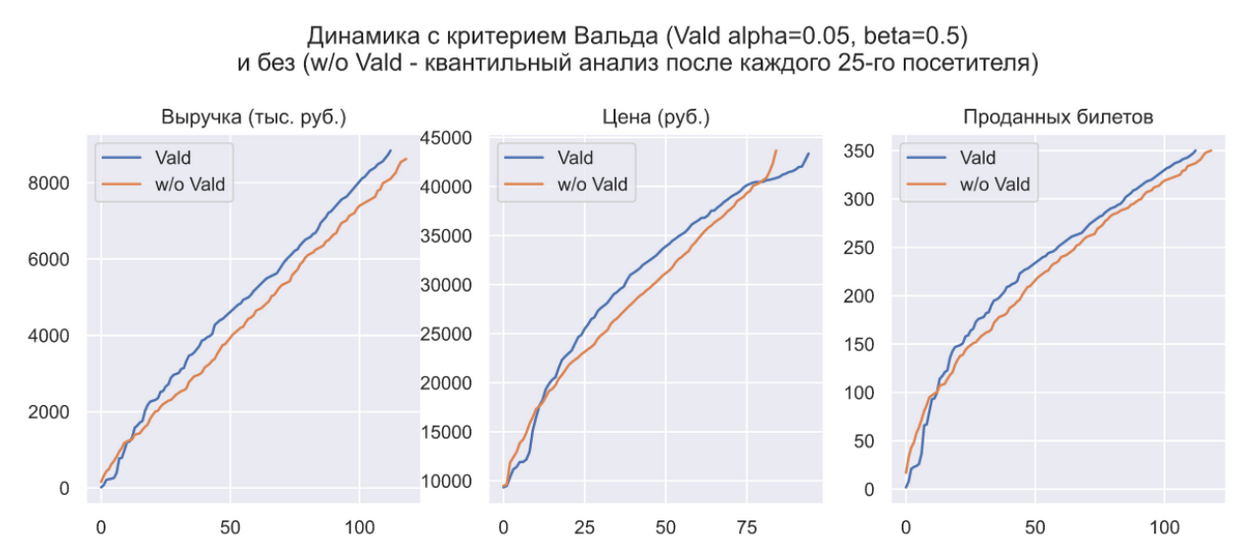
Критерий Вальда нужен лишь для того, что бы задать уровень статистической значимости выводов о том где сейчас находится вероятность продажи одной единицы товара. Например, если мы склонны доверять имеющейся аналитике о параметрах распределения спроса, то можем значительно снизить уровни ошибок первого и второго рода, что будет равносильно увеличению фиксированного количества посетителей после которого выполняется квантильный анализ:
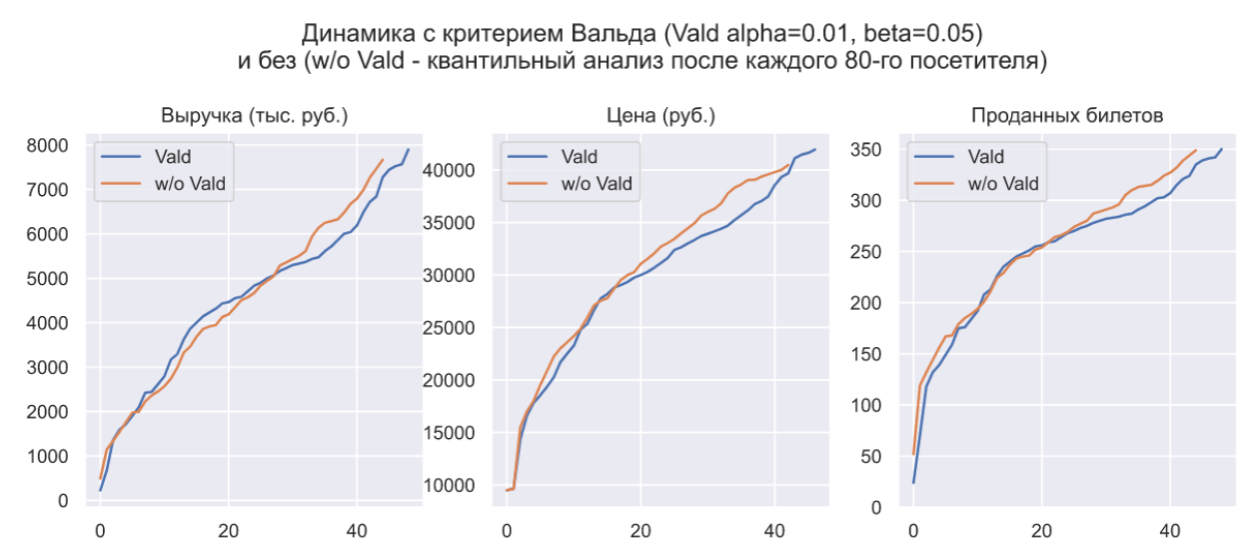
В данном случае мы можем наблюдать некоторое уменьшение выручки и уменьшение количества изменений цены (из-за которого, во многом, и произошло снижение выручки). Фактически, критерий Вальда даже не участвует в формировании цены, которым занимается квантильный анализ и нужен лишь для того, что бы определить частоту его выполнения. В критерии Неймана-Пирсона эта частота является фиксированной, но в критерии Вальда она зависит от величины ошибки, т.е. чем ошибочнее изменение цены, тем скорее оценка вероятности продажи одной единицы товара покинет зону безразличия, а значит мы скорее отреагируем на эту ошибку и попытаемся ее исправить. В данном примере трудно продемонстрировать достоинство такого поведения, потому что спрос хоть и является динамическим, но имеет стационарные приращения. Тем не менее, такая особенность критерия Вальда может оказаться особенно полезной для динамического спроса с нестационарными приращениями.
В определенной степени, уровни ошибок первого и второго рода в критерии Вальда можно отнести к классу гиперпараметров, т.е. параметров которые подбираются эмпирически.
Конечно, это крайне искусственный и очень простой пример, призванный показать, что критерий Вальда и квантильный анализ могут быть применены для динамического спроса. По мере приближения моделей к реальным условиям их сложность сильно возрастает. Например, выше мы договорились, что закон изменения отклонения с течением времени считается известным, но как быть если и он является неизвестным? Ответ на этот вопрос проще продемонстрировать. Предположим, что спрос зависит от времени и распределен как
Python
t = np.random.randint(0, 100, 100000)
mu = 0.5*t + 10
sigma = 0.1*t + 5
data = norm.rvs(mu, sigma)
sns.histplot(data)
plt.xlabel('Количество денег которое посетитель готов отдать за товар');

Данное распределение является смесью (суммой) бесконечного количества нормальных распределений и может быть задано следующим образом:
Python
def norm_mix(mu0, sigma0, k1, k2):
t = np.arange(0, 100)
mu = k1*t + mu0
sigma = k2*t + sigma0
x = np.c_[np.linspace(-20, 120, 300)]
y = norm.pdf(x, mu, sigma)
y = y.sum(axis=1)
y = y/np.trapz(y)
return x, y
plt.plot(*norm_mix(10, 5, 0.5, 0.1));

Это распределение является двухпараметрическим, т.е. оно так же как и нормальное распределение имеет параметры смещения и масштаба, но помимо них обладает еще двумя параметрами формы —
Python
mu0 = [10, 10, 25, 25]
sigma0 = [5, 10, 5, 10]
k1 = [0.5, 0.2, 0.5, 0.7]
k2 = [0.1, 0.3, 0.1, 0.05]
for i in range(4):
plt.plot(*norm_mix(mu0[i], sigma0[i], k1[i], k2[i]),
label=fr'$k_{1} = {k1[i]}$, $k_{2} = {k2[i]}$, $\mu_{0} = {mu0[i]}$, $\sigma_{0} = {sigma0[i]}$');
plt.legend();
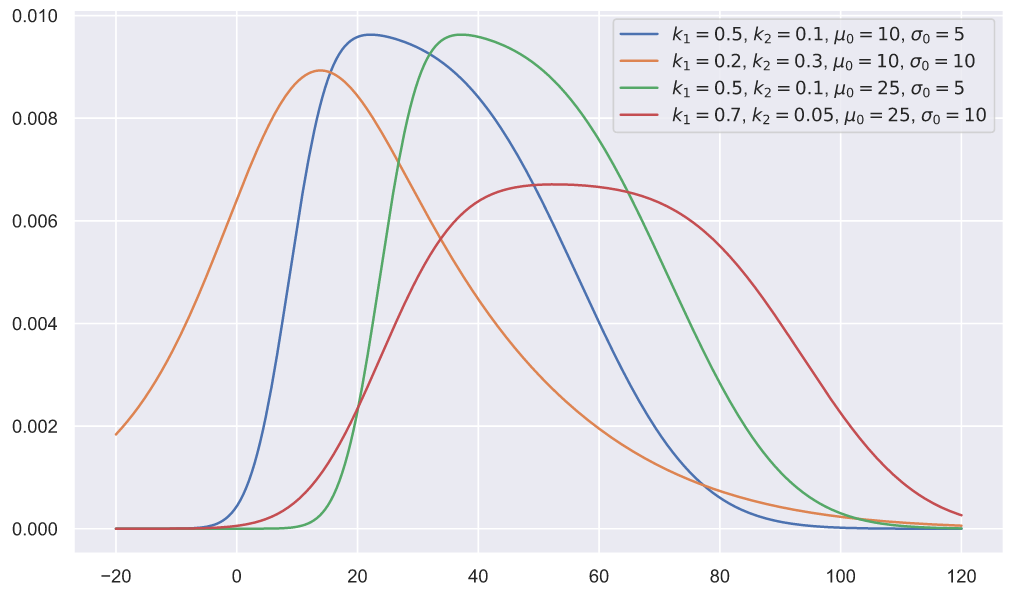
Если не рассматривать только фиксированные временные интервалы (например для вышеприведенного графика все распределения построены для
В заключение
Если несколько раз (в данном случае 50) сравнивать работу данного алгоритма с текущим положением дел в ценообразовании авиабилетов, то картина получается следующая:
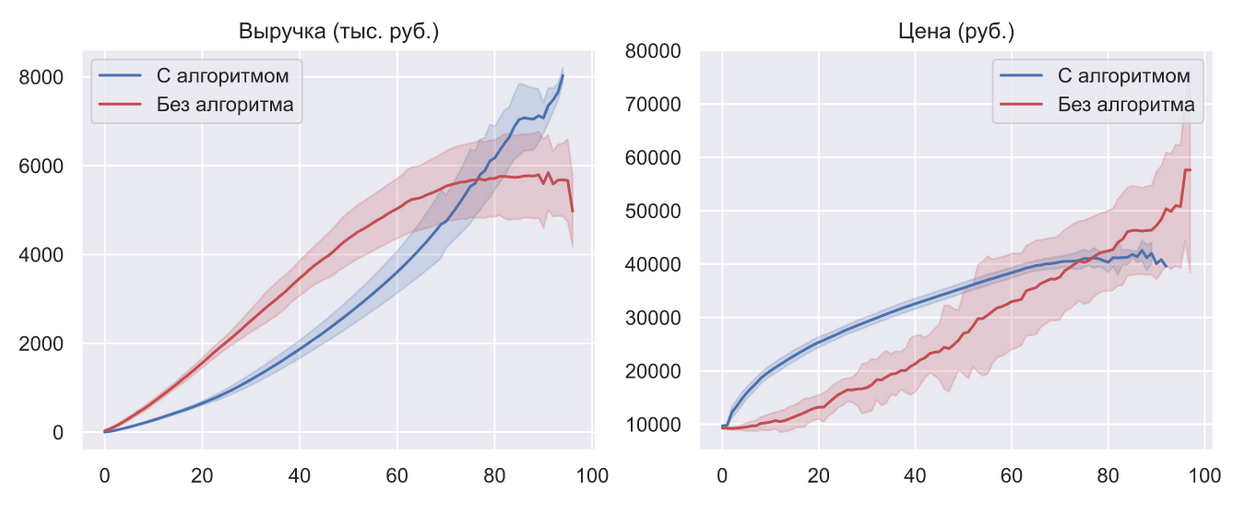
Линиями показаны мат. ожидания, а доверительные интервалы — это стандартные отклонения.
В данном случае под текущим положением дел понимается единственная и простейшая стратегия которая сейчас используется — ручное управление. С одной стороны может показаться, что такую стратегию практически невозможно смоделировать с учетом всей ее сложности. Однако, с определенной «высоты» (и с точки зрения конечного потребителя), вся эта система ведет себя как единственный продавец, который понимает все механизмы только на интуитивном уровне. Поскольку, в качестве цели мы ставили условие максимизации выручки при постоянном наличии билетов в продаже и их полной реализации, то все, что может делать данный продавец — менять цену, пытаясь выровнять скорость продажи билетов с учетом их оставшегося количества. В данном случае «менять цену» означает «угадать цену», т.е. изменение цены является случайной величиной из равномерного распределения, границы которого подобраны так, что бы стратегия удовлетворяла целевым условиям. Вот такая модель текущего положения дел.
Опять же, такое сравнение нельзя назвать абсолютно корректным, но оно дает возможность хотя бы приблизительно оценить прирост выручки обеспеченный ценообразованием на основе квантильного анализа, который можно оценить интервалом от 25% до 35%. Эти цифры вовсе неудивительны, поскольку в режиме ручного управления просто невозможно постоянно угадывать самую оптимальную цену. В случае единичных продаж без ручного управления не обойтись, но когда речь идет о масштабе целой авиакомпании — оно становится серьезным недостатком, который заставляет завышать стоимость билетов и терпеть серьезные убытки.
Вся данная статья базируется на одной простой гипотезе о том, что спрос имеет нормальное распределение. Казалось бы, на том же самом Kaggle полно данных по онлайн торговле и можно легко доказать или опровергнуть эту гипотезу. Но это не было целью данной статьи, так как проблема вовсе не в этом. Здесь мы хотели упрощенно продемонстрировать те подходы, которые используем при решении оптимизационных задач. В своем кругу мы иногда шутим, говоря, что статистическое управление — это то же самое, что управление автомобилем по зеркалу заднего вида, причем довольно маленькому и заляпанному. Ведь смысл оптимального управления заключается не только в том, чтобы найти лучшую стратегию, но еще и в том что бы выполнять ее оптимальную коррекцию на основе поступающих данных о спросе. Как раз коррекция и является самым слабым местом в управлении.
Безусловно, задача динамического ценообразования крайне актуальна для отрасли гражданских авиаперевозок, но как уже говорилось выше, даже если предположить, что у нее есть самое оптимальное решение, то от него все равно не будет никакого толка, если авиакомпания выполнит неоптимальную расстановку авиапарка или выберет для него неоптимальные маршруты. Представленный алгоритм ценообразования, при самых оптимистичных оценках позволяет добиться лишь 10%-го увеличения прибыли в сравнении с алгоритмом сэмплирования Томпсона. Это может показаться хорошим результатом, но на самом деле, если принять во внимание текущее положение дел глобальных логистических процессов, то эти 10% всего лишь капля в море той прибыли, которая упускается всеми игроками. Поэтому в следующей статье мы постараемся рассмотреть модели оптимизации использования судов, планирования расписания и формирования ценообразования как единую задачу.






