Фильтрация шума очень важная вещь, при работе с различными датчиками. Сигнал, получаемый от них всегда приходит с шумами, и важно уметь их грамотно отфильтровать. Качественная фильтрация шума способна уменьшить погрешность и увеличить качество измерения датчика. Этим мы сегодня и займемся.
Примерами будут три графика - синусоида, квадратный сигнал (или дискретный, или цифровой) и треугольный сигнал (или пилообразный).
Код для вывода графиков
import matplotlib.pyplot as plt
from math import sin
# Generals variables
length = 30
resolution = 20
# Creating arrays with graphic
sinus_g = [sin(i / resolution) for i in range(length * resolution)]
square_g = [(1 if p > 0 else -1) for p in sinus_g]
triangle_g = []
t = -1
for _ in range(length * resolution):
t = t+0.035 if t < 1 else -1
triangle_g.append(t)
# Output of graphs
graphics = [sinus_g, square_g, triangle_g]
fig, axs = plt.subplots(3, 1)
for i in range(len(graphics)):
axs[i].plot(graphics[i])
axs[i].set_ylim([-2, 2]), axs[i].set_xlim([0, length*resolution]),
axs[i].set_yticklabels([]), axs[i].set_xticklabels([])
plt.show()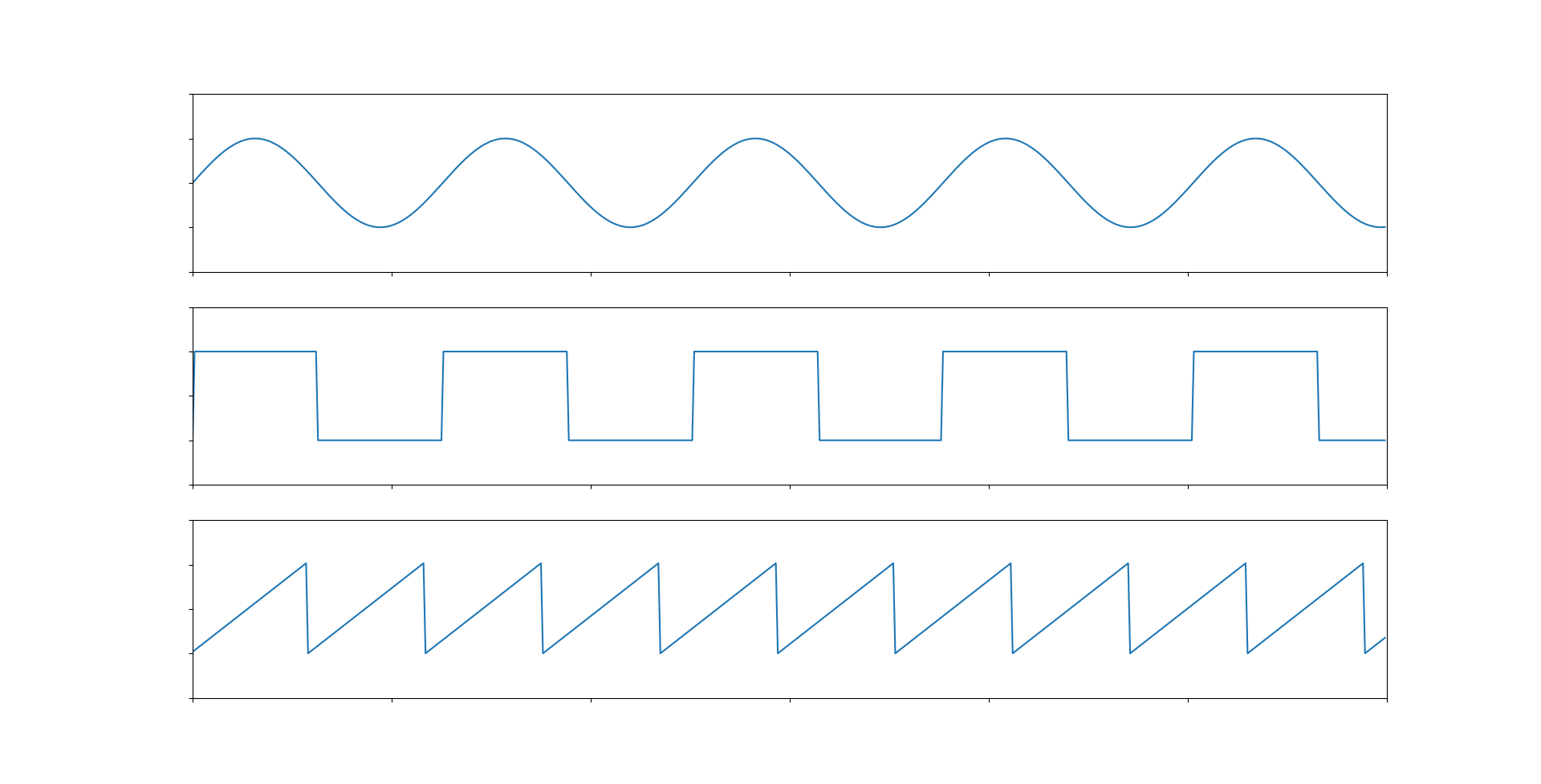
Бороться мы будем с двумя видами шума: постоянный шум (аддитивный белый гауссовский шум или АБГШ) с относительно стабильной амплитудой и случайные импульсы, вызванные внешними факторами. Амплитудой шума - стандартное отклонение зашумленного сигнала от не зашумленного.
Симулировать это мы будем данным образом.
Функция для добавление шума
def noised(func, k=0.3, prob=0.03):
o = []
for p in func:
r = (np.random.random()*2-1) * k
# Standard noise and random emissions
if np.random.random() < prob: c = p + r*7
else: c = p + r
o.append(c)
return o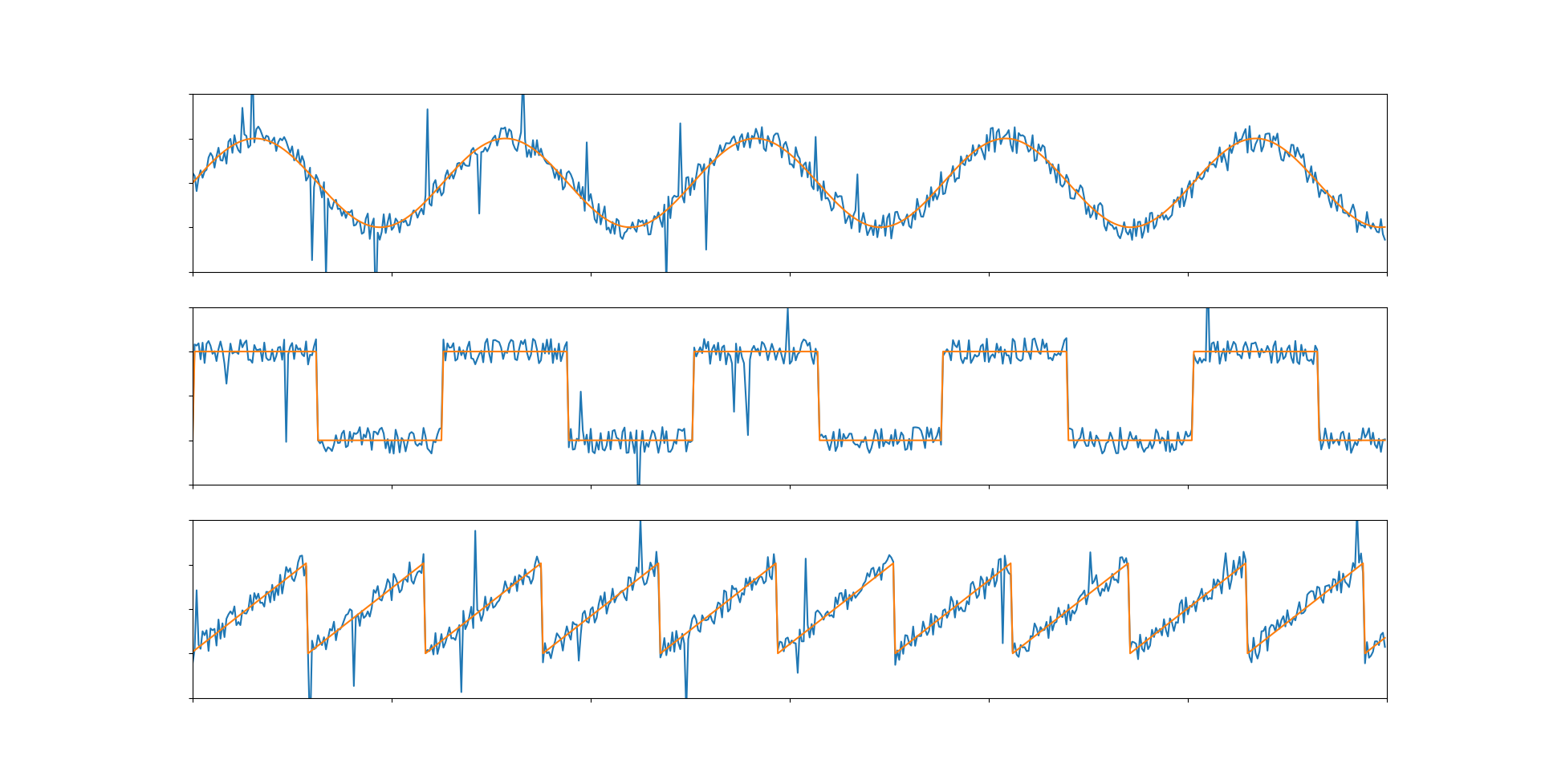
Среднее арифметическое
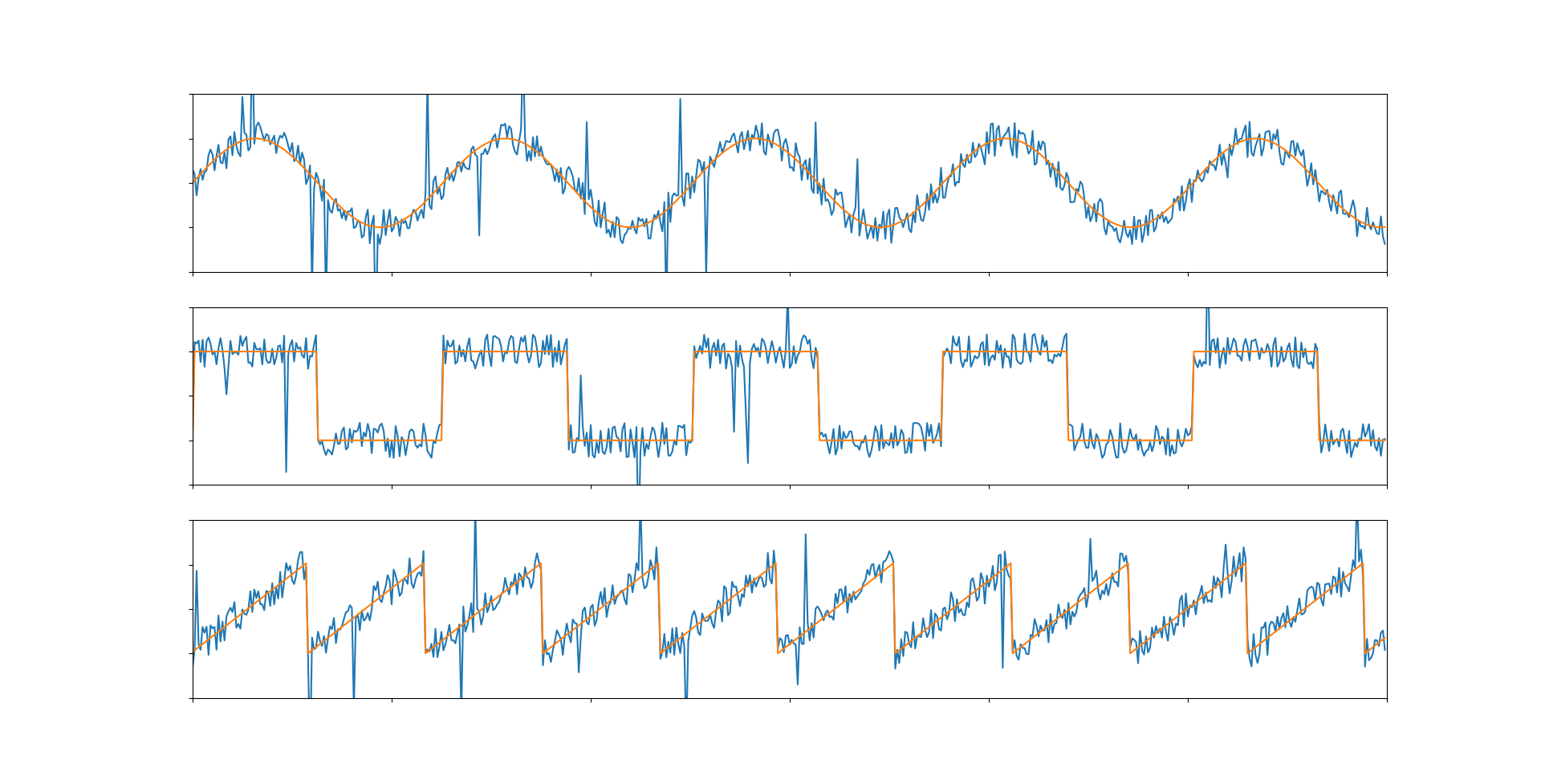
Как по мне, самый очевидный способ минимизировать шум. Для его реализации потребуется ввести буфер нескольких предыдущих значений, каждый раз, когда опрашивается датчик буфер сдвигается (первый элемент удаляется, а новое значение датчика добавляется в конец или как-нибудь по другому, главное фиксированный размер буфера). От его размера и будет зависеть результат и быстродействие кода. С фильтрацией алгоритм справляется очень неплохо. Но его проблема заключается в производительности. Контроллеру приходится делать множество вычислений с плавающей точкой, что может сказаться на скорости выполнения кода. Но если датчик не следует очень часто опрашивать, то этот метод отлично подойдет.
Код фильтрация графика средним арифметическим
def arith_mean(f, buffer_size=10):
# Creating buffer
if not hasattr(arith_mean, "buffer"):
arith_mean.buffer = [f] * buffer_size
# Move buffer to actually values ( [0, 1, 2, 3] -> [1, 2, 3, 4] )
arith_mean.buffer = arith_mean.buffer[1:]
arith_mean.buffer.append(f)
# Calculation arithmetic mean
mean = 0
for e in arith_mean.buffer: mean += e
mean /= len(arith_mean.buffer)
return mean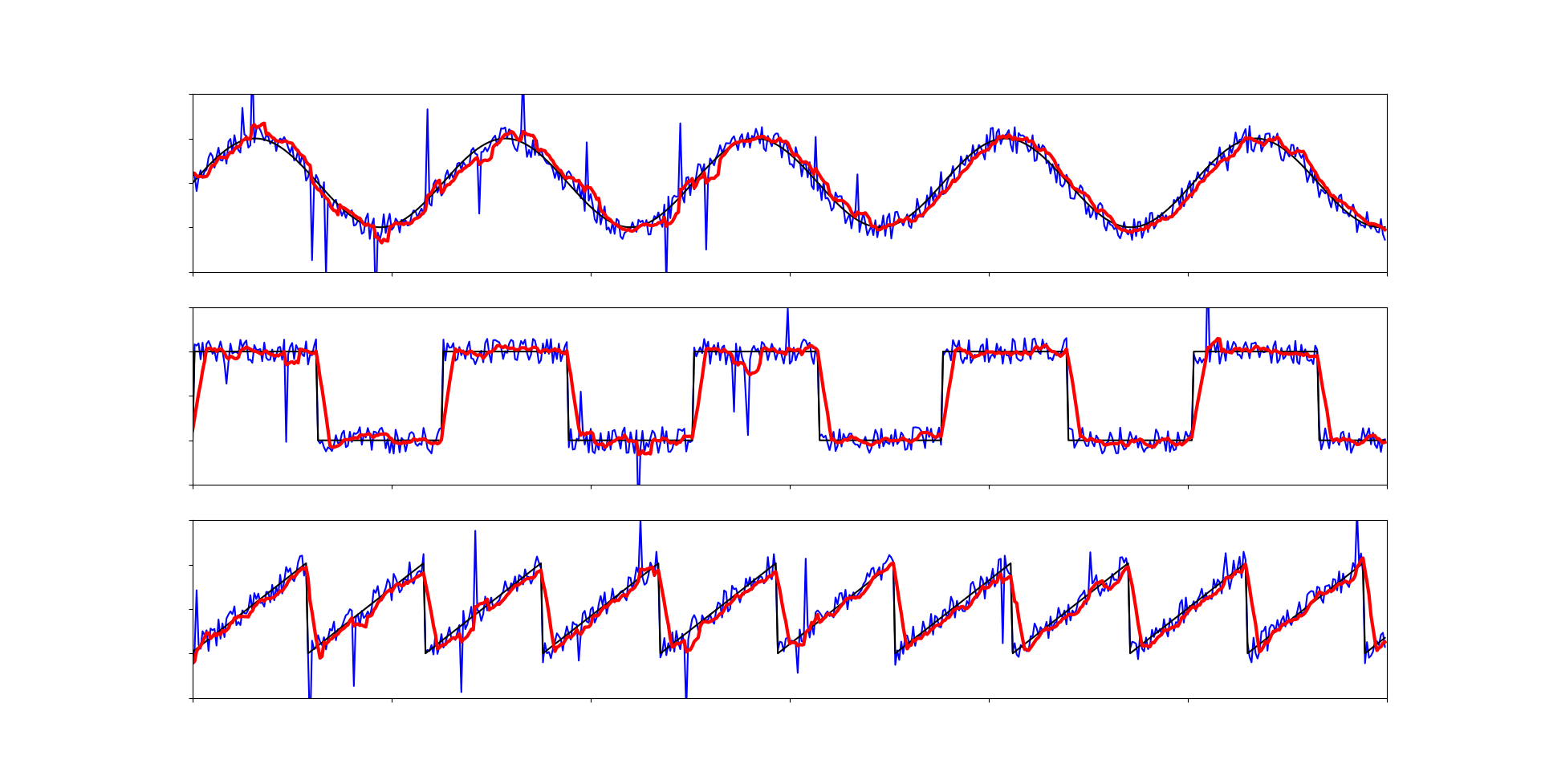
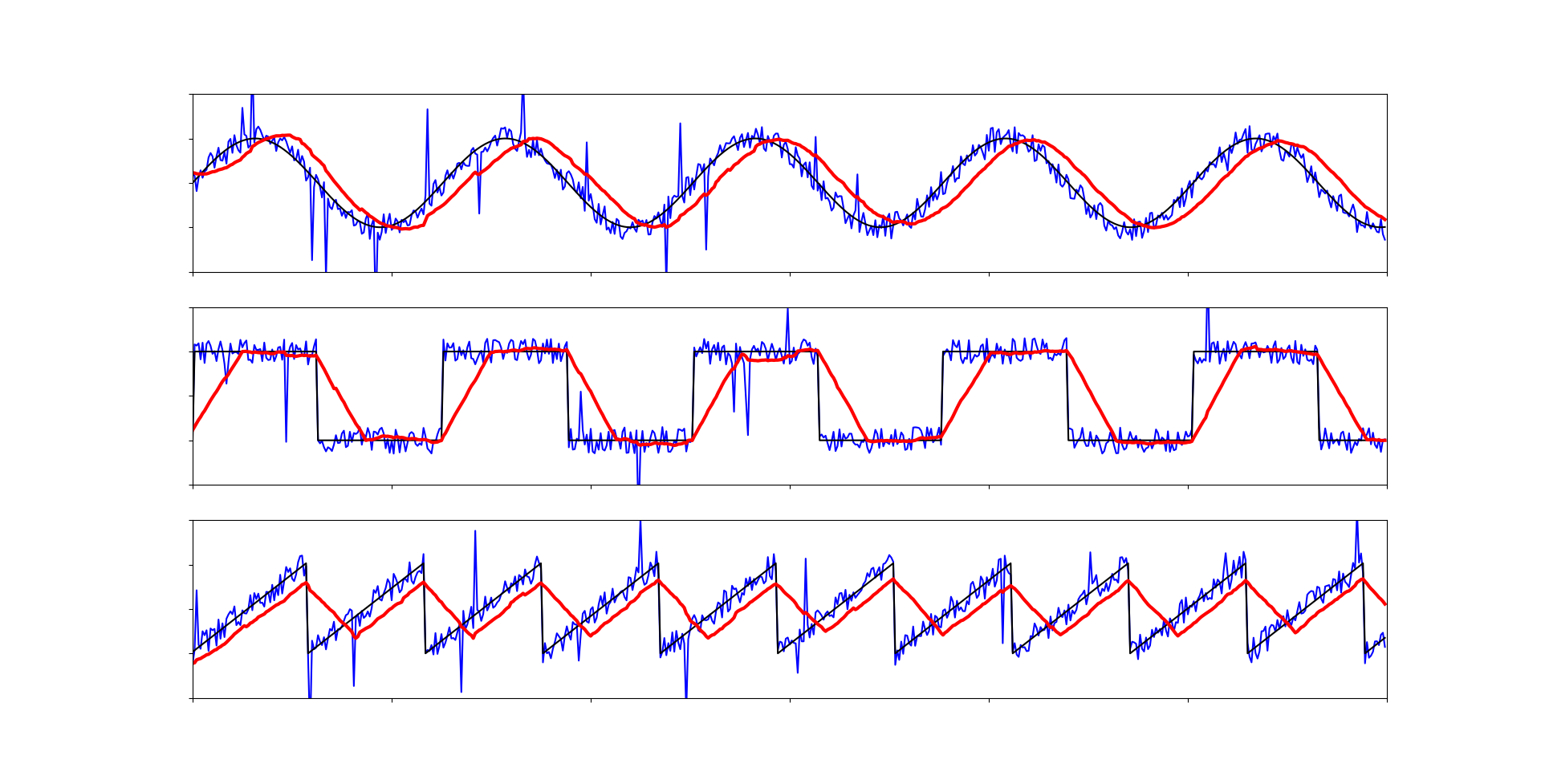
Как мы видим, при увеличении буфера квадратный и треугольный сигналы сильно исказились, а синусоида сместилась. Проявляется запаздывание среднего значения. Так что, при использовании данного фильтра стоит аккуратнее подбирать размер буфера.
Медианный фильтр
Медианный фильтр предназначен справляться со случайными импульсами. Если среднее арифметическое получая на вход (10, 12, 55), выдаст 25.67, то медиан выдаст 12. На первый взгляд не так просто понять как он устроен, но со своей задачей он справляется отлично. На просторах интернета я нашел лаконичное исполнение. Но оно подойдет только в случаях когда длительность импульса не более одного шага, иначе придется использовать другое исполнение медианы высшего порядка.
middle = (max(a,b) == max(b, c)) ? max(a, c) : max(b, min(a, c)); // c++middle = max(a, c) if (max(a, b) == max(b, c)) else max(b, min(a, c)) # pythonКод медианного фильтра
def median(f):
# Creating buffer
if not hasattr(median, "buffer"):
median.buffer = [f] * 3
# Move buffer to actually values ( [0, 1, 2] -> [1, 2, 3] )
median.buffer = median.buffer[1:]
median.buffer.append(f)
# Calculation median
a = median.buffer[0]
b = median.buffer[1]
c = median.buffer[2]
middle = max(a, c) if (max(a, b) == max(b, c)) else max(b, min(a, c))
return middle
Медианный фильтр справился почти со всеми импульсами. К тому же этот алгоритм совершенно прост в вычислении. И используя его в комбинации с каким-либо другим другим фильтром можно получить максимальный результат.
Экспоненциальное бегущее среднее и адаптивный коэффициент
Этот фильтр по своей сути схож с первым, а главное он более простой по вычислениям. Работает он так: к предыдущему фильтрованному значению прибавляется новое, и каждое из них помножено на собственный коэффициент, сумма которых равна 1. Коэффициент k подбирается от 0 до 1 и означает важность нового значения по сравнению с предыдущем, то есть чем больше k, тем больше важность нового нефильтрованного значения и фильтрованный график ближе к изначальному.
normalised = new * k + normalised * (1-k) # Эта формулаnormalised += (new - normalised) * k # А лучше этаАдаптивный коэффициент нужен для корректной фильтрации квадратных сигналов. Реализуется он в одну строчку и означает, что если предыдущее фильтрованное значение слишком далеко от нового (то есть корректный сигнал изменился), то k увеличиваем чтобы момент смены сигнала был четко виден, а иначе k оставляем нормальным.
k = s_k if (abs(new - normalised) < d) else max_kКод фильтра экспоненциального бегущего среднего с адаптивным коэффициент
def easy_mean(f, s_k=0.2, max_k=0.9, d=1.5):
# Creating static variable
if not hasattr(easy_mean, "fit"):
easy_mean.fit = f
# Adaptive ratio
k = s_k if (abs(f - easy_mean.fit) < d) else max_k
# Calculation easy mean
easy_mean.fit += (f - easy_mean.fit) * k
return easy_mean.fit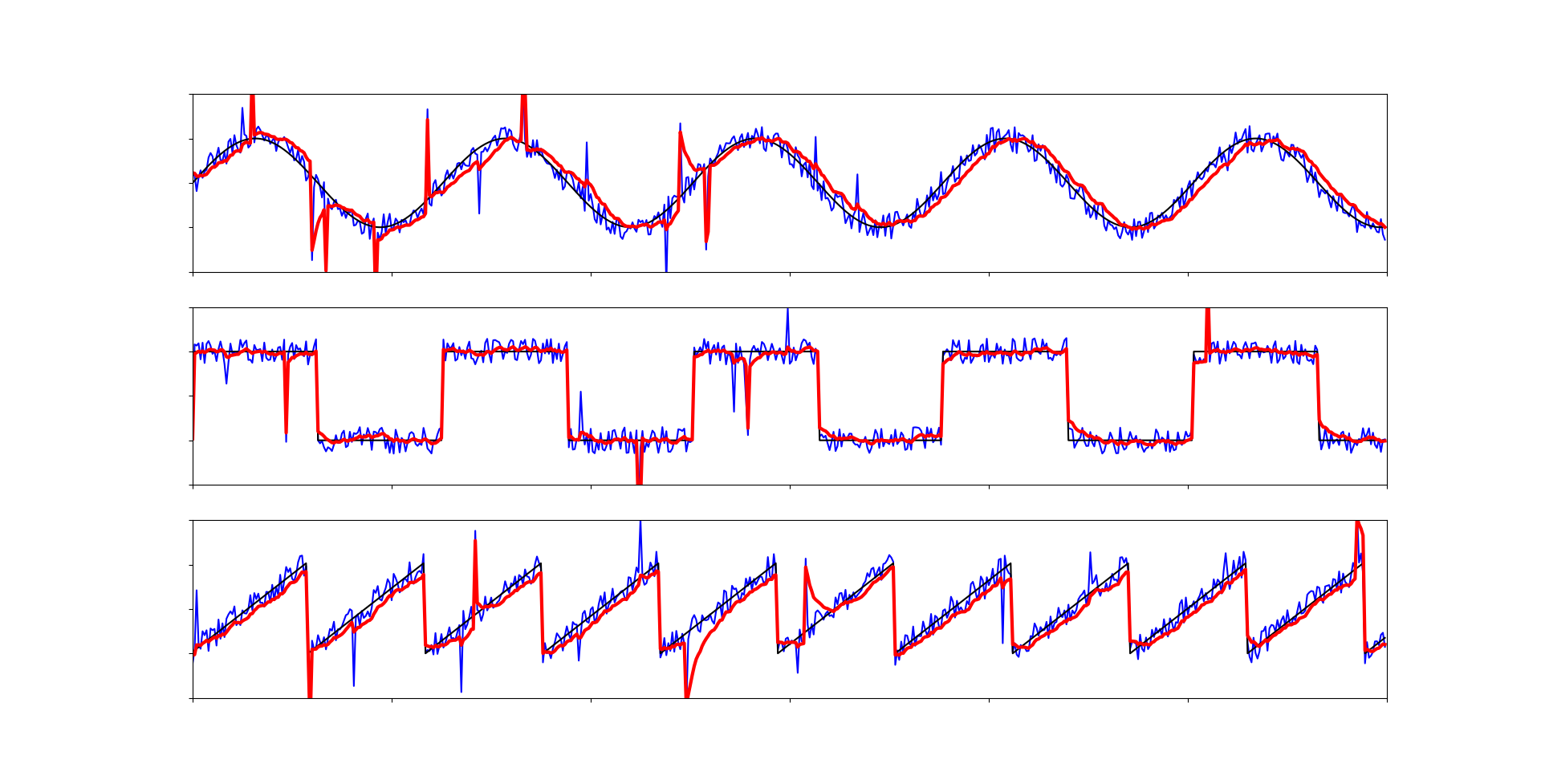
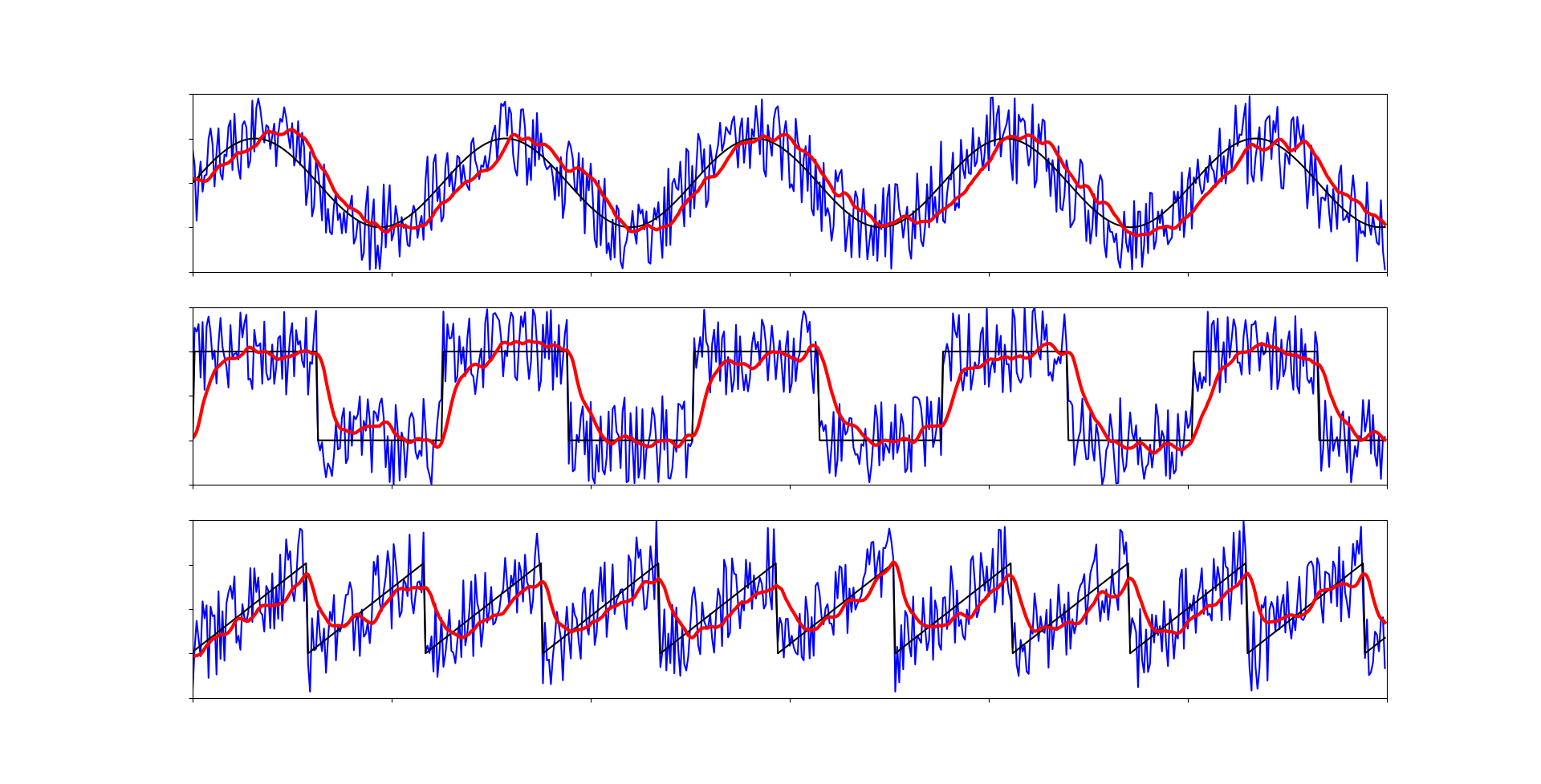
Работает достаточно хорошо, но из-за адаптивного коэффициента появляются некие артефакты в моментах с импульсами, так как они достаточно велики, чтобы определиться как составляющие квадратного сигнала. С этим можно бороться, увеличивая параметр d (требуемое расстояние для определения квадратного сигнала), но есть решение элегантнее. И тут нам как раз нам потребуется медианный фильтр. Если перед подачей данных на бегущее среднее, прогнать их через медиану, то можно получить качественный и быстродейственный алгоритм для фильтрации сигнала.
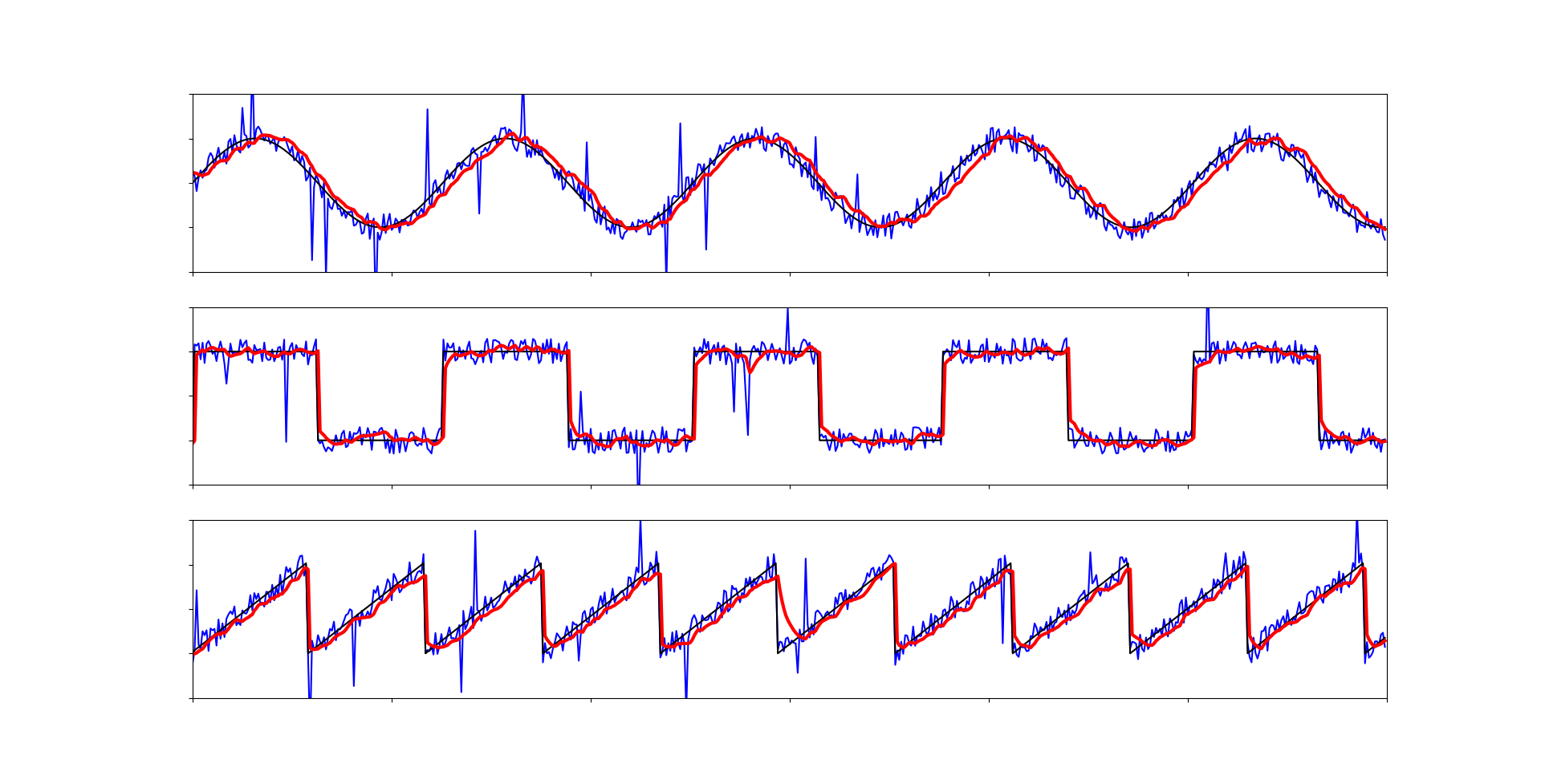
Все артефакты исчезли. Данная связка алгоритмов является одной из самых эффективных и быстродейственных. Она может быть применена практически везде.
Применение связки фильтров
def normalise(func):
o = []
for p in func:
res = median(p)
res = easy_mean(res)
o.append(res)
return oФильтр Калмана
Еще один фильтр, принцип работы которого не столь очевиден для каждого. Из всего кода необходимо знать, что r - это приблизительная амплитуда шума, а q - ковариационное значение процесса, и его следует подбирать самостоятельно. Если вы хотите разобраться в устройстве фильтра Калмана поподробнее, можете прочитать эту статью с википедии, а код я взял и отредактировал с этой страницы.
Код фильтра Калмана
def kalman(f, q=0.25, r=0.7):
if not hasattr(kalman, "Accumulated_Error"):
kalman.Accumulated_Error = 1
kalman.kalman_adc_old = 0
if abs(f-kalman.kalman_adc_old)/50 > 0.25:
Old_Input = f*0.382 + kalman.kalman_adc_old*0.618
else:
Old_Input = kalman.kalman_adc_old
Old_Error_All = (kalman.Accumulated_Error**2 + q**2)**0.5
H = Old_Error_All**2/(Old_Error_All**2 + r**2)
kalman_adc = Old_Input + H * (f - Old_Input)
kalman.Accumulated_Error = ((1 - H)*Old_Error_All**2)**0.5
kalman.kalman_adc_old = kalman_adc
return kalman_adc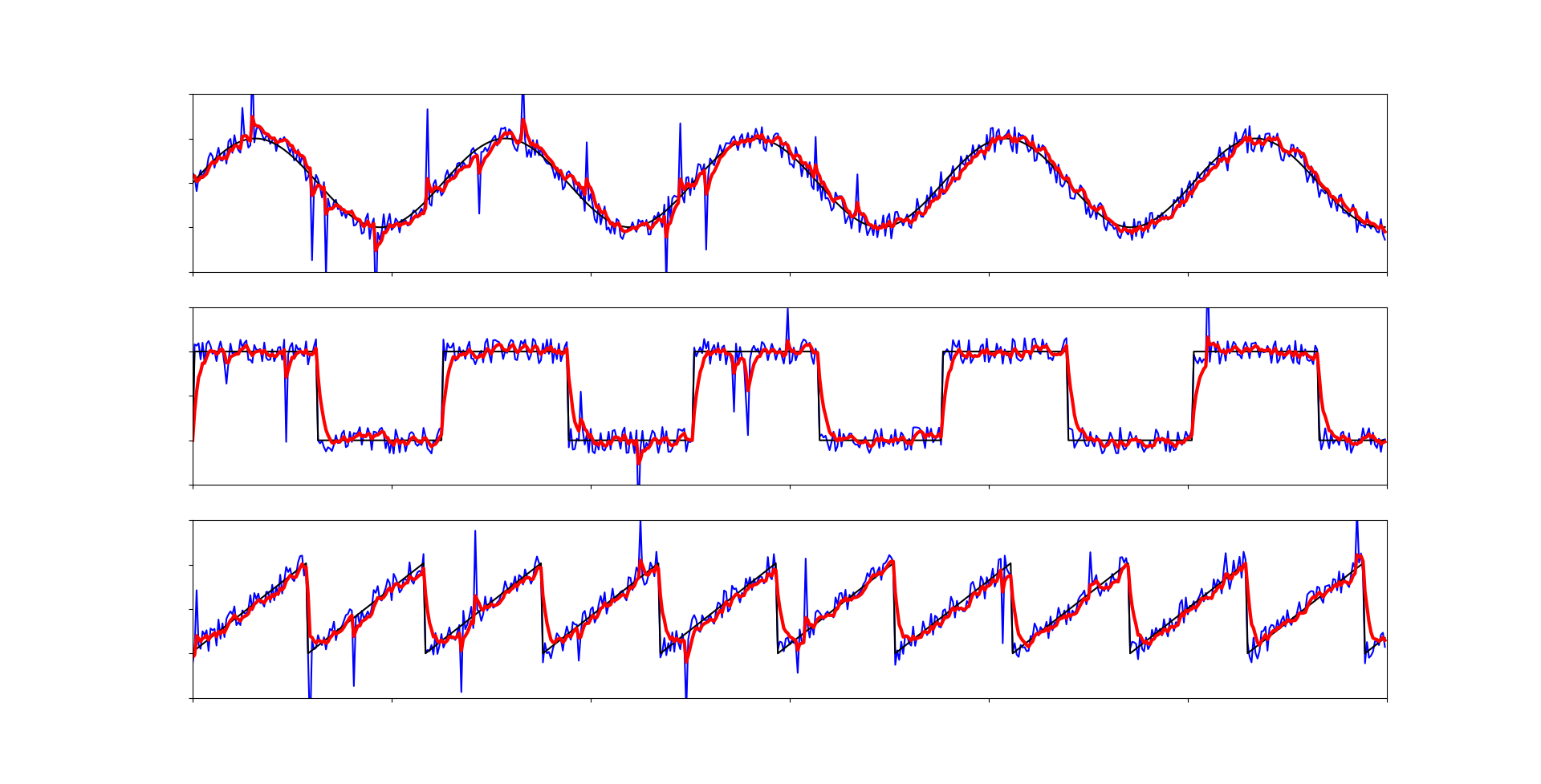
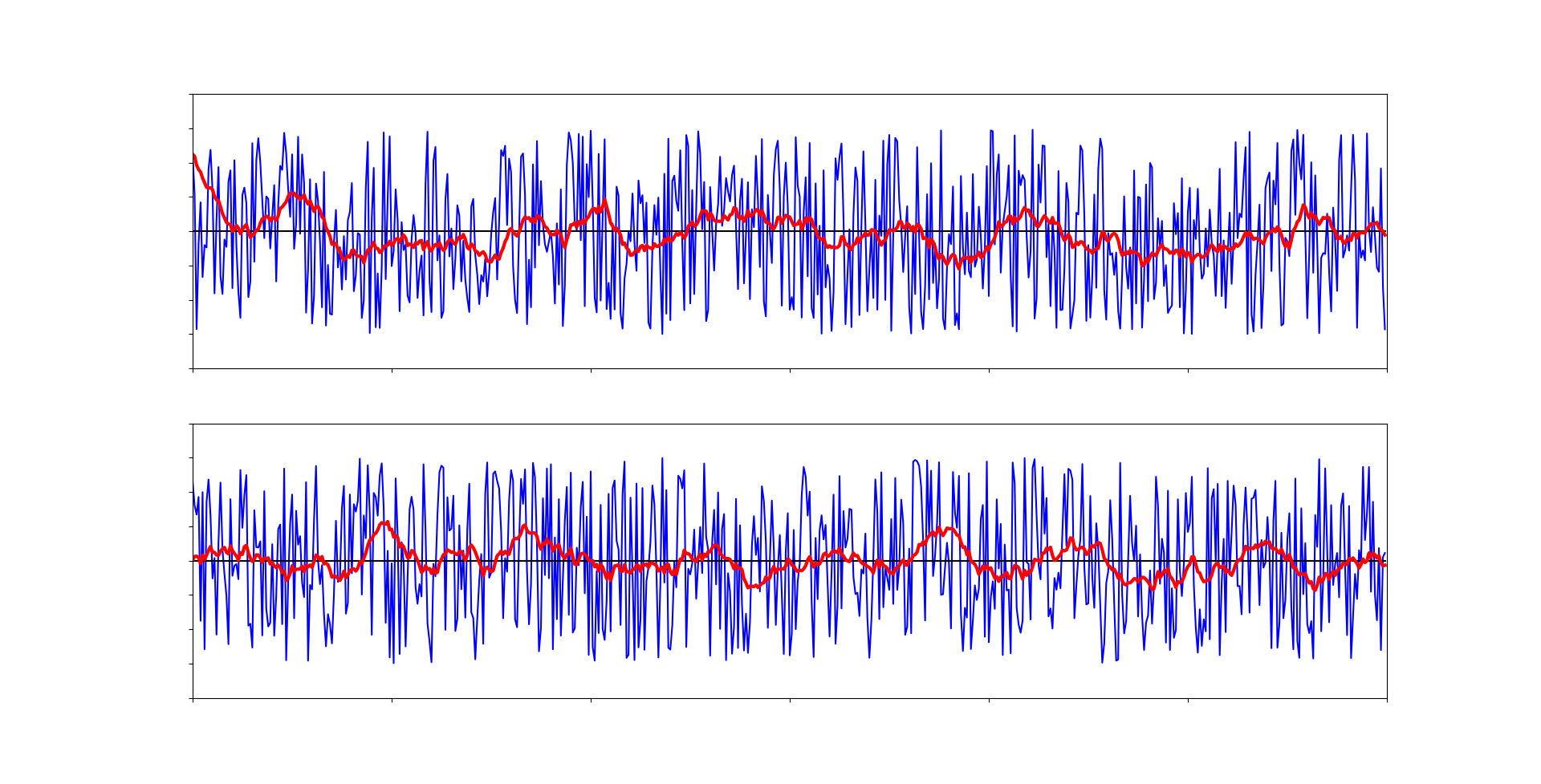
Со своей задачей фильтр справляется, но он не всегда подойдет из-за множества вычислений с плавающей точкой.
Какой фильтр выбрать?
Это зависит от обстоятельств в которых фильтр будет использоваться. Естественно стоит попробовать каждый, но практически для каждого случая подойдёт вариант №2 из списка ниже. Напомню, что наиболее выгодная связка - медианного фильтра с другим. Пройдемся вкратце по перечисленным фильтрам из данной статьи:
Медианный фильтр - самый быстродейственный алгоритм, применятся для отсеивания случайных импульсов, наиболее эффективен в связках с другими алгоритмами.
Экспоненциальное бегущее среднее с адаптивным коэффициент - универсальный, и простой фильтр, подойдет в большинстве ситуаций
Среднее арифметическое - эффективный, но не всегда столь быстродейственный алгоритм
Фильтр Калмана - универсальный способ фильтрации любого сигнала, но громоздкий по вычислениям
Кстати, если вы работаете со средой arduino, то там присутствует удобный инструмент визуализации графиков из значений переданных в порт, статья об этом. Это может упростить работу с сигналами.
В данной статье я не стал затрагивать большую часть терминологии ради доступности. И естественно, фильтры предоставленные в этой статье - это лишь малая часть от всех существующих, и если вы не нашли интересующую информацию по данной теме или предоставленные фильтры не дали достаточный результат, то я рекомендую поподробнее разобраться в теме цифровой фильтрации.
И на последок исходники кодов, и еще несколько примеров...
Код для визуализация графиков
import matplotlib.pyplot as plt
from math import sin
from _f import *
# Generals variables
length = 30
resolution = 20
# Creating arrays with graphic
sinus_g = [sin(i / resolution) for i in range(length * resolution)]
square_g = [(1 if p > 0 else -1) for p in sinus_g]
triangle_g = []
t = -1
for _ in range(length * resolution):
t = t+0.035 if t < 1 else -1
triangle_g.append(t)
# Output of graphs
graphics = [sinus_g, square_g, triangle_g]
fig, axs = plt.subplots(3, 1)
for i in range(len(graphics)):
noised_f = noised(graphics[i])
axs[i].plot(noised_f, color='blue')
axs[i].plot(graphics[i], color='black')
axs[i].plot(normalise(noised_f), linewidth=3, color='red')
axs[i].set_ylim([-2, 2]), axs[i].set_xlim([0, length*resolution]),
axs[i].set_yticklabels([]), axs[i].set_xticklabels([])
plt.show()
Код с фильтрами
import numpy as np
np.random.seed(58008)
def normalise(func):
o = []
for p in func:
res = median(p)
res = easy_mean(res)
o.append(res)
return o
def noised(func, k=0.3, fitob=0.03):
o = []
for p in func:
r = (np.random.random()*2-1) * k
# Standard noise and random emissions
if np.random.random() < fitob: c = p + r*7
else: c = p + r
o.append(c)
return o
def arith_mean(f, buffer_size=10):
# Creating buffer
if not hasattr(arith_mean, "buffer"):
arith_mean.buffer = [f] * buffer_size
# Move buffer to actually values ( [0, 1, 2, 3] -> [1, 2, 3, 4] )
arith_mean.buffer = arith_mean.buffer[1:]
arith_mean.buffer.append(f)
# Calculation arithmetic mean
mean = 0
for e in arith_mean.buffer: mean += e
mean /= len(arith_mean.buffer)
return mean
def easy_mean(f, s_k=0.2, max_k=0.9, d=1.5):
# Creating static variable
if not hasattr(easy_mean, "fit"):
easy_mean.fit = f
# Adaptive ratio
k = s_k if (abs(f - easy_mean.fit) < d) else max_k
# Calculation easy mean
easy_mean.fit += (f - easy_mean.fit) * k
return easy_mean.fit
def median(f):
# Creating buffer
if not hasattr(median, "buffer"):
median.buffer = [f] * 3
# Move buffer to actually values ( [0, 1, 2] -> [1, 2, 3] )
median.buffer = median.buffer[1:]
median.buffer.append(f)
# Calculation median
a = median.buffer[0]
b = median.buffer[1]
c = median.buffer[2]
middle = max(a, c) if (max(a, b) == max(b, c)) else max(b, min(a, c))
return middle
def kalman(f, q=0.25, r=0.7):
if not hasattr(kalman, "Accumulated_Error"):
kalman.Accumulated_Error = 1
kalman.kalman_adc_old = 0
if abs(f-kalman.kalman_adc_old)/50 > 0.25:
Old_Input = f*0.382 + kalman.kalman_adc_old*0.618
else:
Old_Input = kalman.kalman_adc_old
Old_Error_All = (kalman.Accumulated_Error**2 + q**2)**(1/2)
H = Old_Error_All**2/(Old_Error_All**2 + r**2)
kalman_adc = Old_Input + H * (f - Old_Input)
kalman.Accumulated_Error = ((1 - H)*Old_Error_All**2)**(1/2)
kalman.kalman_adc_old = kalman_adc
return kalman_adc
Ещё интересный эксперимент: я построчно загрузил зашумленную картинку своего кота и пропустил её через фильтр Калмана.







