Как врать с помощью статистики

"Существуют три вида лжи:

• ложь;

• наглая ложь;

• пропаганда статистика;

• источник цитаты в интернете".

  Марк Твен (ну или не он).

В данной статье мы рассмотрим, как можно быстро доказать следующие утверждения, смотря на один и тот же источник данных:

• Лошади бегают по часовой стрелке быстрее чем против.

• Лошади бегают против часовой стрелки быстрее чем по часовой.

• Лошади бегают на более дальние дистанции быстрее (с большей скоростью), чем на короткие.

• Лошади бегают на более дальние дистанции медленнее (с меньшей скоростью), чем на короткие.

Данные

Будем рассматривать датасет по скáчкам в Белмонте. В нём содержится информация об имени лошади, году, скорости, дистанции, времени и направлении забега. Анализировать будем с помощью python и библиотек pandas и seaborn.

Для начала прочитаем данные:

import pandas as pd
import seaborn as sns

data = pd.read_csv("path", sep="\t")
df = data[["Length", "Seconds", "Speed"]]

Постараемся узнать, в какую сторону лошади бегают быстрее (по часовой или против часовой стрелки). Очень быстрый и простой способ сравнить два распределения - построить "ящики с усами" или box plot

На данной картинке можно рассмотреть box plot для нормального распределения:

• жирная черта в центре - медиана;

• "коробка" включает в себя 50% результатов, слева от неё находится 25% результатов с самым маленьким значением, справа - 25% с самым большим;

• "усы" иногда покрывают всё распределение целиком, иногда не включают выбросы, каждый из которых отрисовывается отдельно.

Сравнение скорости бега лошадей по и против часовой стрелки

Вообще для уверенности в своём ответе необходимо воспользоваться методами проверки статистических гипотез, но это, если вы действительно хотите узнать результат, наша же цель - показать возможные ошибки в анализе данных, доказать нашу точку зрения, ну или хотя бы создать скандал. Да и проверять гипотезы сложно, а смотреть на графики легко, поэтому просто нарисуем две "коробки", если медиана одной будет находиться вне коробки другой - можно с уверенностью утверждать, что лошади бегают в одну сторону быстрее.

sns.boxplot(x="Speed", y="Direction", data=data)

Скорость бега лошадей против часовой стрелки значимо отличается от скорости бега по часовой, дело закрыто, идём писать статью, что сила Кориолиса влияет на бег лошадей и выбивать себе грант на устройство гонок в южном полушарии и экваторе.

Доказательство того, что лошади бегают на дальние дистанции с меньшей скоростью

Здравый смысл подсказывает, что на дальних дистанциях лошадь больше устаёт и потому её скорость должна быть меньше, проверим так ли это.

df = (df - df.mean()) / df.abs().max()
corr = df.corr()
sns.heatmap(corr, cmap=sns.color_palette("coolwarm", 19))

Как видим, скорость негативно коррелирует с длиной трассы.

Внезапное открытие №1: время прохождения трассы сильно коррелирует с её длиной.

Доказательство того, что лошади бегают на дальние дистанции с большей скоростью

Построим линейную регрессию для значения скорости, заодно сравним между собой эти регресии для разных направлений движения:

sns.lmplot(data=data, y="Speed", x="Length", hue="Direction")

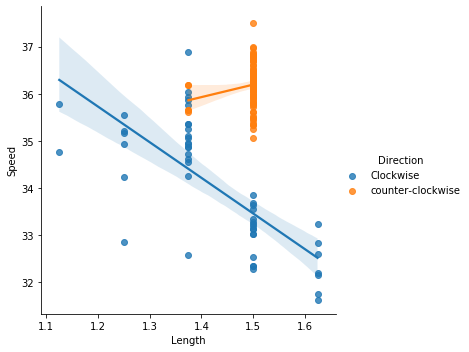
На графике видно, что скорость лошадей, бегущих по часовой стрелке сильно падает с увеличением длины трассы, а вот для лошадей, бегущих против часовой - зависимость обратная.

Внезапное открытие №2: Лошади бегают дальние дистанции с большей скоростью, но только, если бегают против часовой стрелки.

Доказательство того, что лошади бегают по часовой стрелке быстрее

Взглянем на данные поподробнее:

data["clock"] = (data["Direction"] == "Clockwise").astype(int)
data["counter"] = (data["Direction"] == "counter-clockwise").astype(int)
data.plot(x="Year", y=["clock", "counter"])

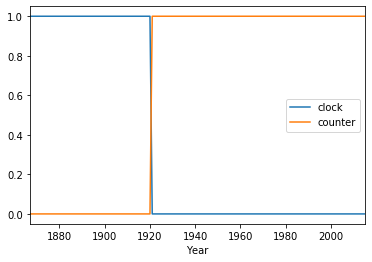
Видно, что лошади сменили направление движения в 1920-ые, вряд ли справедливо сравнивать результаты, между которыми прошло больше века, селекция, улучшение тренировок и новые корма могли сказаться на результате значительнее, поэтому построим линейную регрессию, для того, чтобы определить, когда результаты росли быстрее и каких бы скоростей достигли лошади, продолжай они бегать в ту же сторону.

sns.lmplot(data=data, y="Speed", x="Year", hue="Direction")

Пока лошади бегали по часовой стрелке их скорость росла гораздо сильнее: с 1860-х по 1920-е она выросла на 4 мили в час (~6,5 км/ч), то есть росла на 1 км/ч каждые десять лет, и, если бы не заговор противо-часо-стрелочников, за последний век они бы ускорились на целых 10 км/ч, вместо того жалкого топтания на месте, который мы видим в правой части графика.

Если вас не убедил данный аргумент и вы считаете, что медленный рост можно объяснить тем, что возможности лошадей вышли на плато (см КДПВ)

sns.regplot(data=data, y="Speed", x="Year", order=3)

То подумайте выгодно ли это лошадям и не заплатили ли им давайте сравним данные за несколько лет до и после смены направления.

sns.scatterplot(data=df, x="Year", y="Length", hue="Direction")

Видно, что 5 лет до и после смены направления лошади бегали одинаковую дистанцию, так что сравнение будет честным. Возьмём 4 года, потому что, кажется, что 5 - слишком много, а 3 - слишком мало. (Ну и на них получается не такой красивый результат).

n_years = 4
df = data[(data["Year"] >= 1921 - n_years) & (data["Year"] <= 1920 + n_years)]
sns.boxplot(x="Speed", y="Direction", data=df, ax=axs[ax_idx])

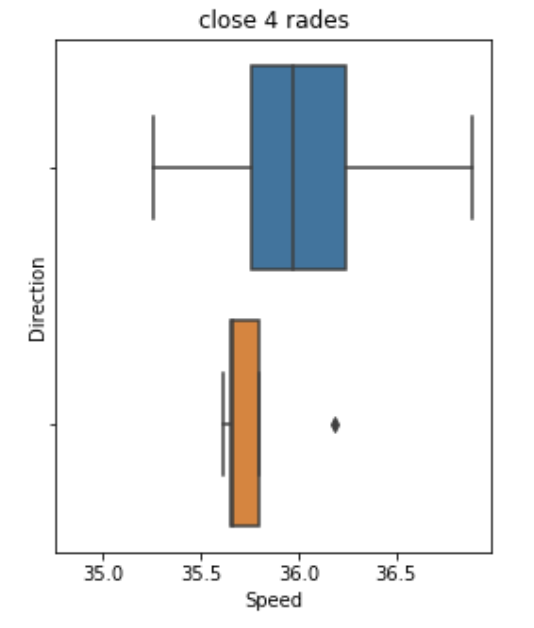
Синий - по часовой.
Оранжевый - против.
Существует значимая разница, лошади бегают по часовой быстрее.

Выводы

В данном примере я пытался показать, что, когда вам кто-то представляет статистические данные и предлагает какие-то выводы на их основе, не спешите соглашаться, спросите:

• Как эти данные получены.

• Нет ли другого объяснения видимым закономерностям.

• Сохраняется ли закономерность, если изменить период наблюдения/страну.

• Однородны ли данные и не осуществлён ли cherry-pick при выборе данных или посчитанных на их основании статистик.

Если же вы сами берётесь за анализ данных внимательно проверяйте свои гипотезы и не спешите с выводами:

• посмотрите на других данных, сохраняется ли найденные вами закономерности;

• нет ли другого объяснения найденным особенностям.