«Умный в гору не пойдёт, умный гору обойдёт». Примерно так рассуждали DS-специалисты при решении задачи, требующей вычисления 10+ млн расстояний между парами точек по их географическим координатам.

До недавнего времени рынок электронной коммерции переживал фазу бурного роста и в связи с этим множество новых фирм начало появляться на этом рынке, а уже существующие компании вынуждены отслеживать ситуацию и оптимизировать свои затраты и способы работы, чтобы повышать эффективность вложений в инфраструктуру. Несколько задач, которые компания, работающая в сфере доставки товаров покупателям, может решать это: понимание достаточности текущей сети точек выдачи груза, не нужно ли открывать дополнительные филиалы, и если нужно, то где именно. Также, например, может быть интересен такой вопрос: а насколько близко к покупателям расположены филиалы одной компании в сравнении с филиалами другой компании (если нам доступны данные и о компании-конкуренте). Рассмотрим решение одной из озвученных задач: для каждой точки выдачи груза найти медианное и среднее расстояния до основных известных клиентов на определенной ограниченной территории, т.е. оценить эффективность расположения.
Пусть нам даны два списка. Первый список, меньший по размеру – это географические координаты расположений пунктов выдачи товара (всего около 1800 точек). Пример данных на рисунке 1.
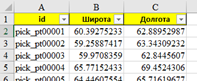
И второй список, гораздо больший по размеру – это географические координаты расположений наших главных клиентов (более 15 тыс. значений в нашем случае). Пример данных Вы можете увидеть на рис.2

И для решения одной из задач, озвученных ранее, нам предстоит для каждой из точек выдачи товара найти список ближайших клиентов, ранжированный по увеличению расстояния до данной рассматриваемой точки выдачи. Учитывая, что список точек выдачи состоит из нескольких тысяч точек, а список клиентов из нескольких десятков тысяч, предстояли достаточно ресурсозатратные вычисления.
Однако, помогла следующая идея. А что, если расстояние измерять не до всех подряд точек, а только среди некоторого, и желательно незначительного по размерам, подмножества? Да, было бы неплохо. Но как отобрать это подмножество быстро и не потерять при этом никаких потенциальных кандидатов? Решение состояло в отборе точек по фильтру: плюс-минус фиксированное значение по широте и плюс-минус другое фиксированное значение по долготе. Python-библиотека pandas позволяет делать такой отбор в одну строчку кода.
def filter_df(df, lattit, longit, eps_latit, eps_longit):
"""
Фильтруем датафрейм с координатами по заданному значению координат (longit, lattit)
заданной погрешностью:
eps_latit по широте;
eps_longit по долготе.
"""
df_filtered = df[(abs(df['Широта'] - lattit) <= eps_latit) &
(abs(df['Долгота'] - longit) <= eps_longit)
]
return df_filteredБлок кода 1. Фильтрация набора точек по вычисленным дельтам для широты и долготы.
Т.е. на плоской Земле это был бы прямоугольник, а в нашем случае (сферическая модель Земли) криволинейная трапеция, т.е. область на поверхности сферической Земли, ограниченная двумя параллелями и двумя меридианами. То, что на самом деле Земля представляет собой эллипсоид, сжатый на полюсах, мы не учитываем – для наших целей точности было достаточно. Размеры нашего условного “прямоугольника” меняются в зависимости от широты, на которой мы рассматриваем точку из первого списка, т.к. длина линии экватора максимальная, а чем ближе к полюсам, тем меньше тот же самый километраж, дающий в сумме одно и то же число градусов долготы.
def one_km_to_degree(lattitiude_deg):
"""
Возвращает, сколько градусов в 1 км для заданной широты.
Если передали широту больше 90, то возвращаем None
"""
if lattitiude_deg > 90:
return None
one_degree_latt = round(ONE_DEGREE_LONGITUDE * m.cos(lattitiude_deg * m.pi / 180), 8)
if one_degree_latt > 0:
return 1 / one_degree_latt
return 0Блок кода 2. Функция расчета кол-ва градусов в 1 км для заданной географической широты
Таким образом, мы получаем подмножество точек нашей выборки, которое, с одной стороны, значительно меньше исходного, а с другой – содержит все нужные нам точки плюс небольшое количество лишних, попавших в углы нашего “прямоугольника”. Отбираем только нужные с помощью расчётов расстояния. Теперь это уже небольшое количество пар значений, для которых можно посчитать обычное декартово расстояние или гаверсинусное, по дуге сферы. Гаверсинус точнее, если точки расположены достаточно далеко друг от друга. Для близких точек разница не значительна и не принципиальна. Но т.к. это стандартная функция библиотеки sklearn, а скорость вычисления быстрая, то используем именно гаверсинус. Подробнее данные шаги можно посмотреть на рисунке 3.
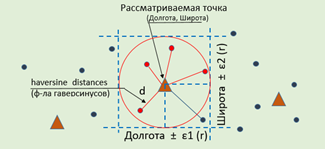
Основные вычисления происходят в следующем коде. Там мы сначала отбираем предварительных кандидатов из всего массива точек, удовлетворяющих нашим условиям, а потом для отобранного подмножества вычисляем расстояния и храним их в словаре для последующего использования в датафрейме.
for row in df_poi.iloc[:, :3].itertuples():
# Берем очередную строку с данными о точке интереса (POI = Point Of Interest)
__, poi_name, poi_latt, poi_long = row
poi_radians = [m.radians(poi_latt), m.radians(poi_long)]
# == Фильтруем для нее выборку с точками заданного квадрата
# Вычисляем дельту по долготе (дельта по долготе вычисл. с помощью
# длины параллели, а длина окружности параллелей уменьш. к полюсам)
eps_longitude = COEFF * self.interest_radius_km * one_km_to_degree(poi_latt)
# После применения фильтра выводим размеры получившегося датафрейма
vsp_local = filter_df(df_check, poi_latt, poi_long, EPS_LATTITUDE, eps_longitude)
t_out = f'Для {poi_name} было отфильтровано {vsp_local.shape[0]}.\n'
write_txt_a(out_max_qty_file, t_out)
# Вычисляем расстояния в словарь, проходясь по всем отфильтрованным значениям координат
dist_calculated = {}
# Если ничего не попало с заданными условиями, то
# записываем одну строчку - "Не найдено" и р-ние 99999 км.
if vsp_local.shape[0] == 0:
df_calc = pd.DataFrame({'id_check_point':['not_found'],
'distance_km': [99999]})
else:
for row_vsp in vsp_local.itertuples():
__, vsp_name, vsp_latt, vsp_long = row_vsp
vsp_radians = [m.radians(vsp_latt), m.radians(vsp_long)]
distance = EARTH_KM * haversine_distances([poi_radians, vsp_radians])[0, 1]
dist_calculated[vsp_name] = distance
# Составляем датафрейм
df_calc = pd.DataFrame(data=dist_calculated.values(), index=dist_calculated.keys())
df_calc.sort_values(by=[0], ascending=True, inplace=True)
df_calc.reset_index(inplace=True)
df_calc.rename(columns={'index': 'id_check_point', 0: 'distance_km'}, inplace=True)
# Убираем тех, кто попал с превышением расстояния
# (из углов предварительного квадрата, например)
df_calc = df_calc[df_calc['distance_km'] <= self.interest_radius_km]
# Если после отбора по расстоянию отбросили все найденные до этого, то создаем строку
if df_calc.shape[0] == 0:
df_calc = pd.DataFrame({'id_check_point':['not_found'],
'distance_km': [99999]})
# Выделяем лидирующие позиции
df_calc = df_calc.head(self.top_n)
df_calc['poi_name'] = poi_name
# Дописываем в конец датафрейм с результатами
df_fin = df_fin.append(df_calc)В результате проведенных расчетов для каждой точки первого списка, получаем список ближайших точек из второго списка, отсортированный по увеличению расстояния (см. рисунок 4).
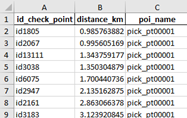
И теперь можно посчитать среднее и медиану по каждой точке второго списка – “poi_name”. Проще всего это сделать с помощью метода groupby в pandas.
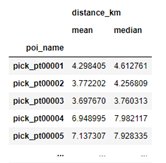
Далее специалист логистической службы может по названию точки вернуться к адресам, а по полученным данным сделать выводы о целесообразности развития данной филиальной сети выдачи товаров.
Полную версию описанного в статье модуля на Python для вычисления попарных расстояний по гео-координатам можно посмотреть на странице проекта в сети Интернет.