Всем привет!В этой статье я расскажу про то, как мы делали автономную машинку на базе нашей ОС Embox, которая детектирует изменение типа поверхности, по которой едет.
Так случилось, что в Новый Год у меня в руках оказалась китайская машинка на радиоуправлении. К сожалению, она не ездила. Чека из магазина у меня не было (машинка была подарком), да и, честно говоря, хотелось её разобрать и посмотреть на элементы схемы. Обычным способом схему было не достать, нужно было выпаивать. Пожалуй, в тот самый момент, когда я взялся за паяльник, я и понял, что вернуть машинку в магазин уже точно не получится. Короче говоря, всю зиму на моём подоконнике так и пылились запчасти, пока однажды мне на глаза не попалась статья от NASA про обнаружение разладки в марсоходе.
Только представьте на минуту: где-то далеко на красной планете едет марсоход, обвешанный датчиками, по поверхности, которую едва ли можно назвать дружелюбной. Поэтому нужно следить за тем, чтобы он не перевернулся, не застрял в песках, не скатился с горки, или наоборот на нее не заехал. Как это сделать? Вот на такой непростой вопрос мне и хотелось ответить.
Марсохода под рукой не оказалось, поэтому я решил сделать машинку с двумя датчиками — гироскопом и акселерометром. И поставил задачу определять две ситуации:
- Машинка начала ехать в горку;
- Машинка начала резко замедляться (например, заехала в песок).
В этой статье я расскажу только о второй ситуации, так как она наиболее завершённая в плане реализации.
Два года назад я купил себе STM32F3-Discovery, в составе которой есть Ecompass (магнитометр + акселерометр) и гироскоп. Вспомнив, что у коллег уже имеется опыт в оживлении машинок, я решил, что можно попробовать применить эту плату.
Оживление машинки
Сдув
Когда машинка завелась и поехала, пришла пора ей управлять. Для этих целей мы реализовали несколько библиотек: управление моторами, управление светодиодами, библиотека сенсоров, библиотека фильтрации сигнала, и, наконец, библиотека алгоритмов обнаружения разладки.
Тестовый полигон или 2 метра поролона
Всем известно, что первым этапом процесса разработки ПО является написание тестов (TDD) и создание тестового окружения. Поэтому прежде чем приступить к решению поставленной задачи, я приступил к разработке методик проверки того, что задача решена корректно. Поскольку оригинальная задача была для марсохода, и у меня не было возможности хорошо сымитировать грунт, я решил воспользоваться доступным подручным средством. Этим подручным средством оказался кусок поролона, который по характеристикам сильно отличался от покрытия стола или пола. Ещё была идея использовать песок, но эксперименты приходилось делать в Питере, в котором постоянно идёт дождь, поэтому пришлось ограничиться «подкрышевыми» методами (но, пожалуй, основная причина заключалось в том, что довольно часто приходилось повторять эксперимент, и бегать туда-сюда было бы накладно).
В общем, в качестве проверки правильности алгоритма я решил, что машинка должна ехать по прямой пока не посчитает, что наехала на “плохую” поверхность, и тогда просто останавливаться и включать светодиод. Вообще, светодиодов предполагалось два, поскольку хотелось, чтобы алгоритм различал проблему, с которой столкнулась машинка. Первая — это поролон, вторая — просто наклонная поверхность.
Для тестирования я запускал машинку на ровной поверхности стола и на столе с прикрепленным к нему поролоном. Важно, что хотелось обнаруживать не только изменение стол->поролон, но при этом игнорировать незначительные неровности (на фото ниже это полоска поролона).
Теперь то, что касается процесса отладки алгоритма. Мы настроили акселерометр на частоту 1344 Hz. В polling-режиме вычитывали значения, и в сыром виде сохраняли во флеш-память. Затем полученные значения из флэш-памяти сохранялись в файл при помощи вызова команды flashdump из отладчика gdb. После того, как у нас появилось достаточно файлов с данными, стало возможным реализовывать и отлаживать алгоритмы на Python, а затем переносить уже отлаженный код в машинку.
Вернемся к нашей задаче
Выше я несколько раз упоминал слово разладка. И на практике это, в общем-то, очень понятное состояние — когда система начинает вести себя необычно. Но вот как формализовать это необычно?
Математически это описывают как “изменение вероятностных характеристик случайного процесса”. Но это совсем общее определение, мы же ограничимся частным случаем. Пусть имеется последовательность случайных переменных
, в нашем случае это показания с датчиков. Будем считать, что это выборка из распределения с некоторой параметрической плотностью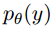 
. Пусть также известно, что в начальный момент времени значение параметра равно некоторому скаляру 
. Под этим мы и будем понимать разладку. Однако, важно отметить, что нам интересны не любые изменения параметра плотности, а только большие некоторого h > 0. Этот параметр h должен зависеть от типа поверхности (то есть это входной параметр алгоритма, который подбирается “на глаз”).Теперь, когда мы выяснили что же мы пытаемся обнаружить, нужно понять как мы это будем делать. Для обнаружения замедления мы использовали показания акселерометра вдоль оси по направлению движения. Как видно из графика, показания зашумлены, поэтому исходная задача разделяется на две подзадачи:
- фильтрация шума;
- обнаружение разладки
Красным отмечен тот фрагмент, на котором произошло замедление. Зеленым — неинтересные нам случайные неровности. Давайте теперь рассмотрим подробнее задачу фильтрации.
Фильтрация шума
Часто задачу о фильтрации ставят таким образом. Рассмотрим
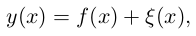
где y(x) — это наблюдаемые переменные (в нашем случае это показания акселерометра), f(x) — настоящий сигнал (без шума),
— шум (считаем, что он имеет стандартное нормальное распределение). Требуется построить оценку 
для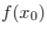 
. Предположим, что f непрерывна (в нашем случае это довольно естественное предположение о непрерывности ускорения). В этом случае для оценки можно использовать обычное среднее:
где
— множество точек наблюдения, 
— мощность множества . Но встает вопрос о том, как же выбрать размер окна, ведь мы ничего не знаем о f. Возможно ли как-то выбирать его динамически, чтобы добиться лучшего результата? Оказывается, что возможно.Как же выбрать окно?
Небольшое философское отступление. На самом деле, конечно же, можно брать скользящее среднее, эмпирически подбирать окно и говорить, что все работает. Но каждый раз из 10 запусков, когда машинка не могла обнаружить препятствие по какой-либо причине, я начинал в этом сомневаться. Поэтому давайте попробуем выжать максимум из тех данных, которые имеем, чтобы максимально хорошо выбрать окно.
Я опирался на статью "On Spatial Adaptive Estimation of Nonparametric Regression". В ней приводятся различные теоретические оценки, но в этой статье я их рассматривать не буду, а расскажу про саму идею. Итак, вопрос состоит в том, как выбрать наилучшее окно, если неизвестна априорная информация о функции f. Чтобы ответить на этот вопрос, оценим верхнюю границу разности ошибки следующим образом: |
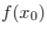— | оценивается как
где
, 
= 
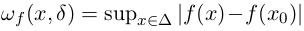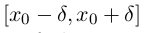. Правая часть неравенства состоит двух частей — детерминированной динамической ошибки 
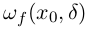, которая полностью определяется функцией f, и стохастической ошибки 
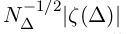, которая полностью не зависит от f. Так как шум в нашем случае имеет стандартное нормальное распределение, ошибку можно ограничить сверху экспонентой (с некоторой вероятностью):
где с > 0, некоторая константа (Здесь я не буду расписывать, почему это так, скажу лишь, что при проверке я пользовался доверительным интервалом для математического ожидания нормальной выборки.)
Пусть выбор оптимального промежутка происходит из
. То есть мы зафиксировали точку и строим вложенные промежутки с центром в этой точке, среди которых пытаемся выбрать наилучший. Тогда, пользуясь ограниченностью ошибки, на каждом из этих промежутков можно получить следующее неравенство:
Легко проверить, что с ростом i детерминистическая ошибка растёт, а стохастическая убывает. Поэтому резонно выбрать окно, которое балансировало бы эти ошибки. Иными словами, требуется найти максимальное I, такое что
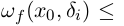
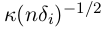. Обозначим 
и будем строить промежутки вида:
,где
это верхняя оценка на 
, что вытекает из предположения что 
. Ясно, что эти отрезки будут иметь общую точку в пересечении — 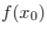. Теперь становится ясно, что нужно строить такие интервалы до тех пор, пока они имеют общую точку пересечения, а затем в качестве окна взять последний построенный (он будет самым большим). Результат применения такого фильтра показан на графиках ниже. Можно видеть, что всплески остались почти неизменными, но при этом сгладились колебания вдоль них.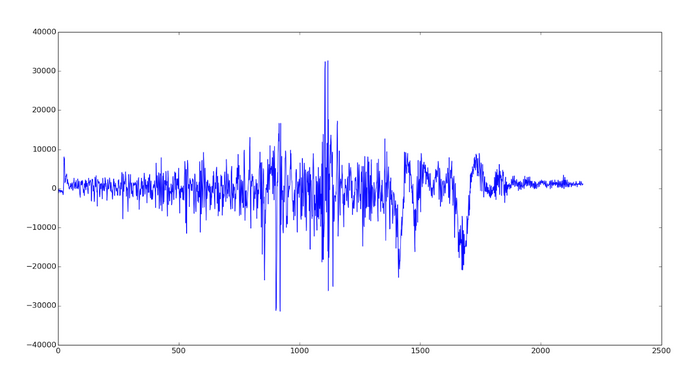
Рис. 1. Исходные сырые данные с акселерометра
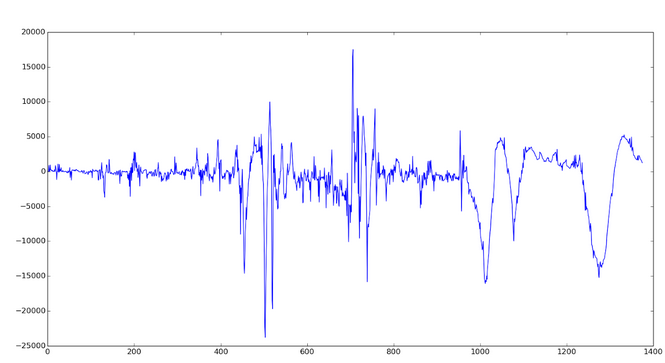
Рис. 2. Результат работы фильтра
Теперь, когда мы научились фильтровать шум, переходим ко второй части — обнаружению разладки.
Filtered Derivative Algorithm
Как я уже писал выше, разладка — это изменение вероятностных характеристик случайного процесса. Примером такой вероятностной характеристики может быть математическое ожидание. Если быть более точным, нас интересует мат. ожидание выборки на каком-то окне. На графике сырых данных видно, что мат. ожидание где-то около 0.
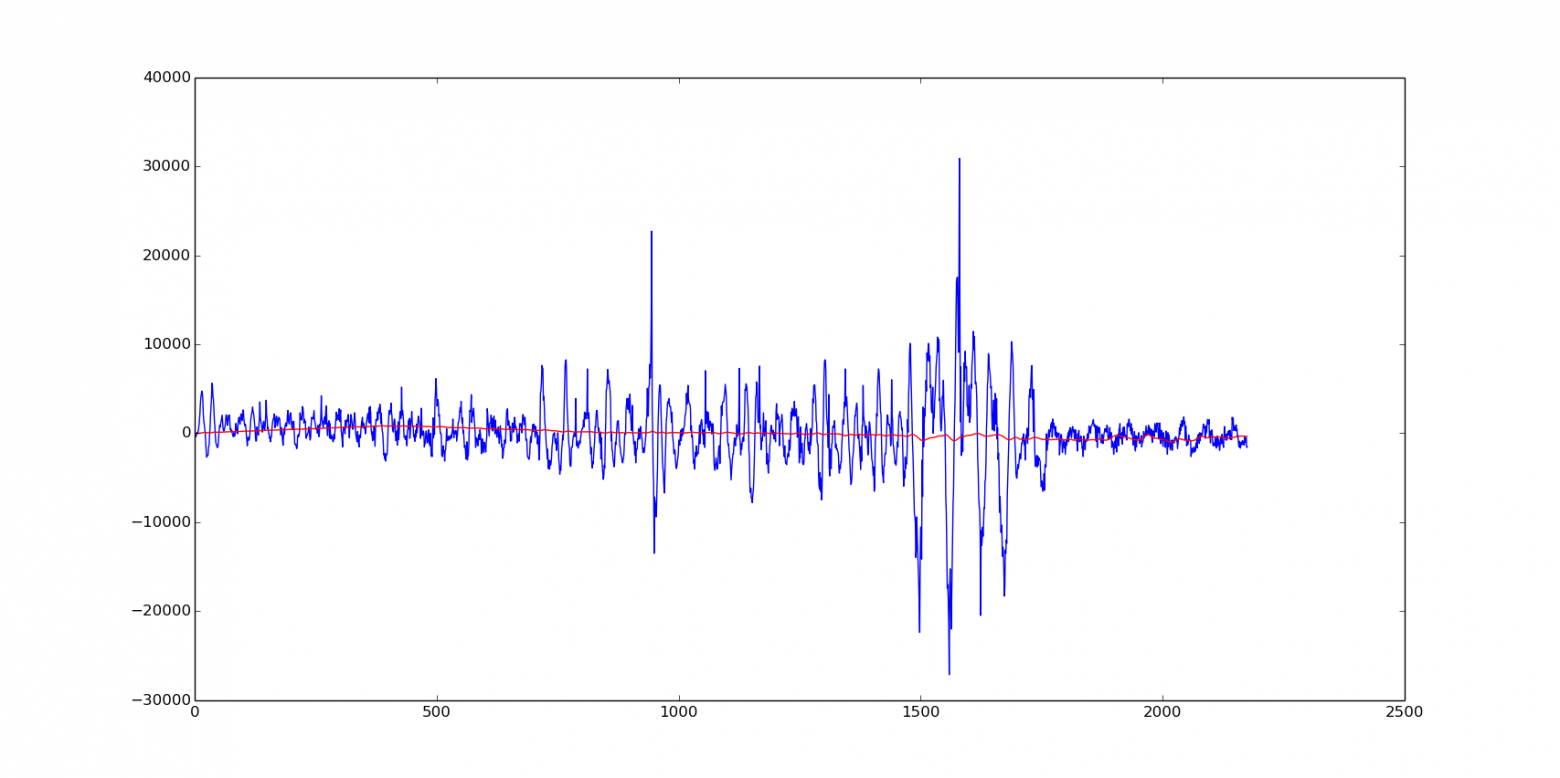
Рис 3. Красная линия — среднее значение выборки на окне размером 200.
А теперь давайте возьмем абсолютное значение ускорения. Как видно из рисунка, имеется всплеск мат. ожидания. Этот всплеск мы и постараемся обнаружить.
Рис 4. Красная линия — среднее значение выборки на окне размером 200.
В основе многих методов обнаружения разладки лежит понятие функции правдоподобия. Эта функция позволяет оценивать параметр плотности распределения, о который мы говорили вначале. Иными словами, она дает оценку на неизвестный параметр, используя известный — показания акселерометра. Чтобы понять, какому из распределений наиболее вероятно принадлежит y, используется логарифм отношения правдоподобий:
(Я не нашёл объяснения, зачем здесь логарифм, но скорее всего — из-за удобства: многие популярные распределения принадлежат к экспоненциальному семейству, а ln убирает экспоненту).
Как правило, интересно не изменение какого-то одного значения, а изменение значений на некотором окне. Для этого можно построить следующую сумму:
где
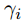— некоторый фильтр, N — размер окна. Давайте теперь ещё раз поймем, что же нас интересует? Мы хотим отслеживать изменение мат. ожидания значений акселерометра вдоль оси x. При этом хотим отслеживать резкое замедление машинки. Иными словами, нас интересует изменение производной функции 
. Так как у нас все дискретно, производная заменяется на разностную схему: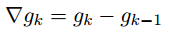
Момент разладки определим как:
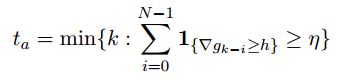
то есть мы считаем количество изменений производной более чем на h, и если число таких изменений больше
, то произошла разладка. В том случае если нас интересует изменение мат. ожидания, то функция принимает вид:
где,
— среднее из двух мат. ожиданий — начального и порогового.Теперь, если в качестве
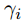взять triangular filter (то есть 
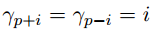) для того чтобы учитывать более поздние данные с меньшим весом, то можно получить следующую формулу (легко проверить на бумаге :))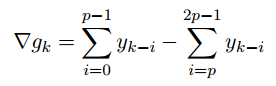
где
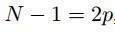. То есть мы отслеживаем то, насколько сильно изменилось среднее значение на соседних окнах. И вот что получилось для машинки:
Рис 5. h = 3000 (линия threshold на графике),
= 1.Результат
Результат работы двух алгоритмов, описанных выше. Еще раз напомню, что должно было произойти — при обнаружении замедления на поролоне машинка зажигает светодиод и выключает моторы.
Заключение
Подводя итог: у нас получилось распознавать серьезное замедление машинки, игнорируя при этом незначительные помехи на её пути. С машинкой я съездил на ТМШ 2015, где мне как раз и подсказали про выбор окна — спасибо за это участникам и преподавателям :)
Если статья покажется вам сносной, то в будущем я мог бы рассказать про наши дальнейшие продвижения — применение фильтра Калмана для детектирования наклонных поверхностей, анализ дисперсии (а не мат. ожидания как в этой статье), да и вообще про то, какие бывают методы для решения подобного рода задач.
Я не приводил в статье фрагменты кода, а дал ссылку на исходники, так как кода не много. Но если появятся вопросы по реализации, буду рад на них ответить.
P.S.
Когда был на ТМШ 2015, несколько ребят интересовались софтом внутри машинки, так что оставляю ссылки на код. Если кому-то будет интересно, можно повторить всё, что описано в статье, самостоятельно. А может, кто-то даже улучшит алгоритм или посоветует, как это можно сделать.