Добрый вечер.
Этот пост посвящён быстрому преобразованию Фурье. Будут рассмотрены прямое и обратное преобразования (в комплексных числах). В следующей части я планирую рассмотреть их применения в некоторых задачах олимпиадного программирования (в частности, одна задача про «похожесть» строк), а также рассказать про реализацию преобразования в целых числах.
БПФ — это алгоритм, вычисляющий значения многочлена степени n=2k в некоторых n точках за время O(n⋅logn) («наивный» метод выполняет ту же задачу за время O(n2)). За то же время можно выполнить и обратное преобразование. Так как складывать, вычитать и умножать массивы чисел гораздо легче, чем многочлены (особенно умножать), БПФ часто применяется для ускорения вычислений с многочленами и длинными числами.
Для начала давайте определимся, что такое многочлен:
P(x)=a0+xa1+x2a2+x3a3+...+xn-1an-1
Если Вы знакомы с комплексными числами, то можете пропустить этот пункт, в противном случае, вот краткое определение:
x=a+ib, где i2=-1
Здесь a называется вещественной (Real) частью, а b — мнимой (Imaginary). В этих числах, как нетрудно заметить, можно извлекать корень из отрицательных (да и вообще любых) чисел — это очень удобно при работе с многочленам — как следует из основной теоремы алгебры, у каждого многочлена степени n имеется ровно n комплексных корней (с учётом кратности).
Также их очень удобно представлять в виде точек на плоскости:

Еще одним замечательным свойством комплексных чисел является то, что их можно представить в виде x=(cosα+isinα)r, где α — полярный угол «числа» (называется аргументом), а r — расстояние от нуля до него (модуль). А при умножении двух чисел:
a=(cosα+i⋅sinα)ra
b=(cosβ+i⋅sinβ)rb
ab=(cosα+i⋅sinα)(cosβ+i⋅sinβ)rarb
ab=(cosα⋅cosβ-sinα⋅sinβ+i(sinα⋅cosβ+cosβ⋅sinα))rarb
ab=(cos(α+β)+i⋅sin(α+β))rarb
Их модули перемножаются, а аргументы складываются.
Теперь давайте поймём, как выглядят комплексные корни n-ой степени из 1. Пусть xn=1, тогда его модуль, очевидно, равен единице, а n⋅argx=2πk, где k — целое. Это обозначает, что после n умножений числа на самого себя (т.е. возведения в n-ю степень) его аргумент станет «кратен» 2π (360 градусам).
Вспомним формулу числа, если известен аргумент и модуль, получаем:
α=2π⋅x/n, где 0x
ωi=cosα+i⋅sinα
Т.е. если порисовать, то мы получим просто точки на окружности через равные промежутки:
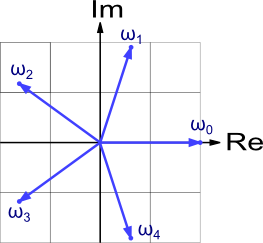
Прошу заметить три вещи, которыми мы будем активно пользоваться (без них ничего не получится):
ωa⋅ωb=ω(a+b)modn
ω0+ω1+ω2+...+ωn-1=0
ω0n/2=ω2n/2=ω4n/2=...=1 (при чётном n)
Из-за этих свойств именно в этих точках мы и будем считать значение многочлена. Разумеется, результаты необязательно будут вещественными, поэтому в программе потребуется работать с комплексными числами.
Доказательство очень простое: пусть φ=ω0+ω1+.... Домножим обе части на ω1 (!= 1). Т.к. ωi⋅ω1=ωi+1, то φ⋅ω1=ω1+ω2+...+ωn-1+ω0. От перестановки слагаемых сумма не меняется, поэтому φ=φ⋅ω1, соответственно φ⋅(ω1-1)=0. Т.к. ω1 != 1, то φ=0.
Будем считать, что наш многочлен имеет степень n=2k. Если нет, дополним старшие коэффициенты нулями до ближайшей степени двойки.
Основная идея БПФ очень проста:
Пусть:
A(x)=a0+xa2+x2a4+...+xn/2-1an-2 (четные коэффициэнты P)
B(x)=a1+xa3+x2a5+...+xn/2-1an-1 (нечётные коэффициенты P).
Тогда P(x)=A(x2)+x⋅B(x2).
Теперь применим принцип «разделяй и властвуй»: чтобы посчитать значения P в n точках (ω0,ω1,...), посчитаем значения A и B рекурсивно в n/2 точках (ω0,ω2,...). Теперь значение P(ωi) восстановить достаточно просто:
P(ωi)=A(ω2i)+ωi⋅B(ω2i)
Если обозначить за ξi=ω2i точки, в которых мы считаем значения многочлена степени n/2, формула преобразится:
P(ωi)=A(ξi)+ωi⋅B(ξi)
Её уже можно загонять в программу, не забыв что i принимает значения от 0 до n-1, а ξi определено лишь от 0 до n/2-1. Вывод — надо будет взять i по модулю n/2.
Время работы выражается рекуррентной формулой T(n)=O(n)+2T(n/2). Это довольно известное соотношение и оно раскрывается в O(n⋅log2n) (грубо говоря, глубина рекурсии — log2n уровней, на каждом уровне суммарно по всем вызовам выполняется O(n) операций).
Вот пример неэффективной рекурсивной реализации БПФ:
Можете добавить ввод-вывод и проверить правильность своей реализации. Для многочлена P(x)=4+3x+2x2+x3+0⋅x4+0⋅x5+0⋅x6+0⋅x7 значения должны получиться такими:
P(w0)=(10.000,0.000)
P(w1)=(5.414,4.828)
P(w2)=(2.000,2.000)
P(w3)=(2.586,0.828)
P(w4)=(2.000,0.000)
P(w5)=(2.586,-0.828)
P(w6)=(2.000,-2.000)
P(w7)=(5.414,-4.828)
Если это так — можете засекать время рекурсивного и наивного метода на больших тестах.
У меня на многочлене степени 212 эта реализация работает 62 мс, наивная — 1800 мс. Разница налицо.
Для того, чтобы сделать процедуру нерекурсивной, придётся подумать. Легче всего, как мне кажется, провести аналогию с MergeSort (сортировка слиянием) и нарисовать картинку, на которой показаны все рекурсивные вызовы:

Как мы видим, можно сделать один массив, заполнить его изначально значениями fft(a0), fft(a4), fft(a2), .... Как несложно понять, номера ai — это «развёрнутые» в двоичном представлении числа 0,1,2,3,.... Например, 110=0012,410=1002 или 6=1102,3=0112. Понять это можно следующим образом: при спуске на нижний уровень рекурсии у нас определяется еще один младший бит (с конца). А при «нормальной» нумерации бит определяется с начала. Поэтому нужно «развернуть» число. Это можно сделать «в лоб» за O(n⋅log2n), а можно динамическим программированием за O(n) по следующему алгоритму:
Теперь придумаем алгоритм, позволяющий нам из «ступеньки» получить ступеньку повыше. Хранить все значения с предыдущего шага мы будем в одном массиве. Как хорошо видно на рисунке, надо обрабатывать данные блоками по k, причём вначале k=1, а потом с каждым шагом увеличивается вдвое. Мы обрабатываем два блока длиной k и получаем на выходе один блок длиной 2k. Давайте на примере разберём, как это делалось рекурсивно, вспомним формулу из начала статьи и повторим:

Аргументами процедуры для слияния двух блоков будут два vector'а (естесственно, по ссылке, исходный и результат), номер стартового элемента первого блока (второй идёт сразу после) и длина блоков. Можно было бы конечно сделать и iterator'ами — для большей STL'ности, но мы ведь всё равно будем переносить эту процедуру внутрь основной для краткости.
И основная процедура преобразования:
На многочлене степени 216 рекурсия работает 640 мс, без рекурсии — 500. Улучшение есть, но программу можно сделать еще быстрее. Воспользуемся тем свойством, что ωi=-ωi+n/2. Значит, можно не считать два раза корень и ai⋅ωj — синус, косинус и умножение комплексных чисел очень затратные операции.
Перехо с такой оптимизацией называется «преобразованием бабочки». Программа стала работать 260 мс. Для закрепления успеха давайте предподсчитаем все корни из 1 и запишем их в массив:
Теперь скорость работы — 78 мс. Оптимизация в 8 раз по сравнению с первой реализацией!
На данный момент весь код преобразования занимает порядка 55 строк. Не сотню, но это достаточно много — можно короче. Дляначала избавимся от кучи лишних переменных и операций в fft_merge:
Теперь можно переместить цикл из fft_merge в основную процедуру (также можно убрать p2, поскольку p2=p1+len — у меня это также дало небольшой выигрыш по времени. Что любопытно, если убрать p1=pdest, то у меня лично выигрыш по времени убивается):
Как видите, само преобразование занимает не так много — 17 строк. Всё остальное — предподсчёт корней и разворот чисел. Если Вы готовы сэкономить код в обмен на время работы (O(n⋅log2n) вместо O(n)), можете заменить 13 строк разворота чисел на следующие шесть:
В результате теперь код выглядит так:
Получить значения многочлена в точках — это, конечно, хорошо, но преобразование Фурье умеет больше — по этим значениям построить сам многочлен, причём за то же самое время! Оказывается, что если применить преобразование Фурье к массиву значений, как к коэффициентам многочлена, потом разделить результат на n и перевернуть отрезок с 1 до n-1 (нумерация с 0), то мы получим коэффициенты исходного многочлена.
Код тут предельно простой — всё уже написано. Думаю, Вы справитесь.
Пусть мы применяем обратное преобразование к многочлену P(x) с коэффициентами vi (исходный многочлен имел коэффициенты ai):
vi=a0+ωia1+ω2ia2+ω3ia+...
Посмотрим на результат преобразования:
bi=v0+ωiv1+ω2iv2+ω3iv3+...
Подставим значения vj (помним, что ωaωb=ωa+bmodn:
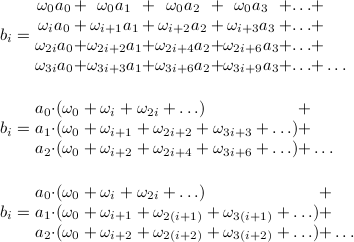
Теперь давайте докажем один замечательный факт: при x≠0, ω0+ωx+ω2x+...+ω(n-1)x=0.
Доказывается аналогично тому, что сумма корней — ноль: обозначим за φ сумму, домножим обе части на ωx и посмотрим, что получилось.
Теперь применим этот факт к вычислению значения bi. Заметим, что все строки, кроме одной, в которой содержится an-i, обнулятся.
Таким образом:
bi=an-i⋅(ω0+ω0+ω0+ω0+...)
bi=an-i⋅n
Что и требовалось доказать.
Вообще говоря, о применении я уже чуть-чуть говорил в начале статьи. В частности, теперь перемножение многочленов можно выполнять следующим образом:
Легко заметить, что время работы этой программы — O(n⋅log2n) и самые трудоёмкие операции — преобразования Фурье. Также можно заметить, что если нам требуется вычислить более сложное выражение с двумя многочленами, то по-прежнему можно выполнять лишь три приобразования — сложение и вычитание также будут работать за линейное время. К сожалению, с делением не всё так просто, поскольку многочлен может случайно принять значение 0 в какой-нибудь из точек. UPD2: не забудьте, что степень произведения двух многочленов степени n будет равна 2n, поэтому при вводе следует добавить «лишние» нулевые старшие коэффициенты.
Если представить число в десятичной (или более) системе счисления, как многочлен с коэффициентами — цифрами, то умножение длинных чисел также можно выполнять очень быстро.
И, напоследок, задача, которую я разберу в следующем посте: у вас есть две строки одинаковой длины порядка 105 из букв A, T, G, C. Требуется найти такой циклический сдвиг одной из строк, чтобы совпало максимальное количество символов. Очевидно наивное решение за O(n2), но есть решение при помощи БПФ.
Удачи!
UPD: Выложил код целиком на pastebin
Этот пост посвящён быстрому преобразованию Фурье. Будут рассмотрены прямое и обратное преобразования (в комплексных числах). В следующей части я планирую рассмотреть их применения в некоторых задачах олимпиадного программирования (в частности, одна задача про «похожесть» строк), а также рассказать про реализацию преобразования в целых числах.
БПФ — это алгоритм, вычисляющий значения многочлена степени n=2k в некоторых n точках за время O(n⋅logn) («наивный» метод выполняет ту же задачу за время O(n2)). За то же время можно выполнить и обратное преобразование. Так как складывать, вычитать и умножать массивы чисел гораздо легче, чем многочлены (особенно умножать), БПФ часто применяется для ускорения вычислений с многочленами и длинными числами.
Определения и способы применения
Для начала давайте определимся, что такое многочлен:
P(x)=a0+xa1+x2a2+x3a3+...+xn-1an-1
Комплексные числа
Если Вы знакомы с комплексными числами, то можете пропустить этот пункт, в противном случае, вот краткое определение:
x=a+ib, где i2=-1
Здесь a называется вещественной (Real) частью, а b — мнимой (Imaginary). В этих числах, как нетрудно заметить, можно извлекать корень из отрицательных (да и вообще любых) чисел — это очень удобно при работе с многочленам — как следует из основной теоремы алгебры, у каждого многочлена степени n имеется ровно n комплексных корней (с учётом кратности).
Также их очень удобно представлять в виде точек на плоскости:

Еще одним замечательным свойством комплексных чисел является то, что их можно представить в виде x=(cosα+isinα)r, где α — полярный угол «числа» (называется аргументом), а r — расстояние от нуля до него (модуль). А при умножении двух чисел:
a=(cosα+i⋅sinα)ra
b=(cosβ+i⋅sinβ)rb
ab=(cosα+i⋅sinα)(cosβ+i⋅sinβ)rarb
ab=(cosα⋅cosβ-sinα⋅sinβ+i(sinα⋅cosβ+cosβ⋅sinα))rarb
ab=(cos(α+β)+i⋅sin(α+β))rarb
Их модули перемножаются, а аргументы складываются.
Комплексные корни из 1
Теперь давайте поймём, как выглядят комплексные корни n-ой степени из 1. Пусть xn=1, тогда его модуль, очевидно, равен единице, а n⋅argx=2πk, где k — целое. Это обозначает, что после n умножений числа на самого себя (т.е. возведения в n-ю степень) его аргумент станет «кратен» 2π (360 градусам).
Вспомним формулу числа, если известен аргумент и модуль, получаем:
α=2π⋅x/n, где 0x
ωi=cosα+i⋅sinα
Т.е. если порисовать, то мы получим просто точки на окружности через равные промежутки:

Прошу заметить три вещи, которыми мы будем активно пользоваться (без них ничего не получится):
ωa⋅ωb=ω(a+b)modn
ω0+ω1+ω2+...+ωn-1=0
ω0n/2=ω2n/2=ω4n/2=...=1 (при чётном n)
Из-за этих свойств именно в этих точках мы и будем считать значение многочлена. Разумеется, результаты необязательно будут вещественными, поэтому в программе потребуется работать с комплексными числами.
Почему сумма корней — ноль
Доказательство очень простое: пусть φ=ω0+ω1+.... Домножим обе части на ω1 (!= 1). Т.к. ωi⋅ω1=ωi+1, то φ⋅ω1=ω1+ω2+...+ωn-1+ω0. От перестановки слагаемых сумма не меняется, поэтому φ=φ⋅ω1, соответственно φ⋅(ω1-1)=0. Т.к. ω1 != 1, то φ=0.
Как работает
Будем считать, что наш многочлен имеет степень n=2k. Если нет, дополним старшие коэффициенты нулями до ближайшей степени двойки.
Основная идея БПФ очень проста:
Пусть:
A(x)=a0+xa2+x2a4+...+xn/2-1an-2 (четные коэффициэнты P)
B(x)=a1+xa3+x2a5+...+xn/2-1an-1 (нечётные коэффициенты P).
Тогда P(x)=A(x2)+x⋅B(x2).
Теперь применим принцип «разделяй и властвуй»: чтобы посчитать значения P в n точках (ω0,ω1,...), посчитаем значения A и B рекурсивно в n/2 точках (ω0,ω2,...). Теперь значение P(ωi) восстановить достаточно просто:
P(ωi)=A(ω2i)+ωi⋅B(ω2i)
Если обозначить за ξi=ω2i точки, в которых мы считаем значения многочлена степени n/2, формула преобразится:
P(ωi)=A(ξi)+ωi⋅B(ξi)
Её уже можно загонять в программу, не забыв что i принимает значения от 0 до n-1, а ξi определено лишь от 0 до n/2-1. Вывод — надо будет взять i по модулю n/2.
Время работы выражается рекуррентной формулой T(n)=O(n)+2T(n/2). Это довольно известное соотношение и оно раскрывается в O(n⋅log2n) (грубо говоря, глубина рекурсии — log2n уровней, на каждом уровне суммарно по всем вызовам выполняется O(n) операций).
Напишем что-нибудь
Вот пример неэффективной рекурсивной реализации БПФ:
Slow FFT
#include <vector>
#include <complex>
using namespace std;
typedef complex<double> cd; // STL-ное комплексное число. Нам нужен double, ведь мы работает с sin и cos
typedef vector<cd> vcd;
vcd fft(const vcd &as) { // Возвращает вектор значений в корнях из 1
int n = as.size();
// Когда-то же надо прекратить рекурсию?
if (n == 1) return vcd(1, as[0]);
vcd w(n); // Считаем корни
for (int i = 0; i < n; i++) {
double alpha = 2 * M_PI * i / n;
w[i] = cd(cos(alpha), sin(alpha));
}
// Считаем коэффициенты A и B
vcd A(n / 2), B(n / 2);
for (int i = 0; i < n / 2; i++) {
A[i] = as[i * 2];
B[i] = as[i * 2 + 1];
}
vcd Av = fft(A);
vcd Bv = fft(B);
vcd res(n);
for (int i = 0; i < n; i++)
res[i] = Av[i % (n / 2)] +
w[i] * Bv[i % (n / 2)];
return res;
}
Можете добавить ввод-вывод и проверить правильность своей реализации. Для многочлена P(x)=4+3x+2x2+x3+0⋅x4+0⋅x5+0⋅x6+0⋅x7 значения должны получиться такими:
P(w0)=(10.000,0.000)
P(w1)=(5.414,4.828)
P(w2)=(2.000,2.000)
P(w3)=(2.586,0.828)
P(w4)=(2.000,0.000)
P(w5)=(2.586,-0.828)
P(w6)=(2.000,-2.000)
P(w7)=(5.414,-4.828)
Если это так — можете засекать время рекурсивного и наивного метода на больших тестах.
У меня на многочлене степени 212 эта реализация работает 62 мс, наивная — 1800 мс. Разница налицо.
Избавляемся от рекурсии
Для того, чтобы сделать процедуру нерекурсивной, придётся подумать. Легче всего, как мне кажется, провести аналогию с MergeSort (сортировка слиянием) и нарисовать картинку, на которой показаны все рекурсивные вызовы:

Как мы видим, можно сделать один массив, заполнить его изначально значениями fft(a0), fft(a4), fft(a2), .... Как несложно понять, номера ai — это «развёрнутые» в двоичном представлении числа 0,1,2,3,.... Например, 110=0012,410=1002 или 6=1102,3=0112. Понять это можно следующим образом: при спуске на нижний уровень рекурсии у нас определяется еще один младший бит (с конца). А при «нормальной» нумерации бит определяется с начала. Поэтому нужно «развернуть» число. Это можно сделать «в лоб» за O(n⋅log2n), а можно динамическим программированием за O(n) по следующему алгоритму:
- Пробежимся циклом от 0 до n-1
- Будем хранить и динамически пересчитывать номер старшего единичного бита числа. Он меняется, только когда текущее число — степень двойки: увеличивается на 1.
- Когда мы знаем старший бит числа, перевернуть всё число не составляет труда: «отрезаем» старший бит (XOR), переворачиваем остаток (уже посчитанное значение) и добавляем «отрезанную» единицу
Теперь придумаем алгоритм, позволяющий нам из «ступеньки» получить ступеньку повыше. Хранить все значения с предыдущего шага мы будем в одном массиве. Как хорошо видно на рисунке, надо обрабатывать данные блоками по k, причём вначале k=1, а потом с каждым шагом увеличивается вдвое. Мы обрабатываем два блока длиной k и получаем на выходе один блок длиной 2k. Давайте на примере разберём, как это делалось рекурсивно, вспомним формулу из начала статьи и повторим:

Аргументами процедуры для слияния двух блоков будут два vector'а (естесственно, по ссылке, исходный и результат), номер стартового элемента первого блока (второй идёт сразу после) и длина блоков. Можно было бы конечно сделать и iterator'ами — для большей STL'ности, но мы ведь всё равно будем переносить эту процедуру внутрь основной для краткости.
Объединение блоков
void fft_merge(const vcd &src, vcd &dest, int start, int len) {
int p1 = start; // Позиция в первом блоке
int en1 = start + len; // Конец первого блока
int p2 = start + len; // Позиция во втором блоке
int en2 = star + len * 2; // Конец второго блока
int pdest = start; // Текущая позиция в результатирующем массиве
int nlen = len * 2; // Длина нового блока
for (int i = 0; i < nlen; i++) {
double alpha = 2 * M_PI * i / nlen;
cd w = cd(cos(alpha), sin(alpha)); // Текущий корень
dest[pdest] = src[p1] + w * src[p2];
if (++p1 >= en1) p1 = start;
if (++p2 >= en2) p2 = start + len;
}
}
И основная процедура преобразования:
vcd fft(const vcd &as) {
int n = as.size();
int k = 0; // Длина n в битах
while ((1 << k) < n) k++;
vi rev(n);
rev[0] = 0;
int high1 = -1;
for (int i = 1; i < n; i++) {
if ((i & (i - 1)) == 0) // Проверка на степень двойки. Если i ей является, то i-1 будет состоять из кучи единиц.
high1++;
rev[i] = rev[i ^ (1 << high1)]; // Переворачиваем остаток
rev[i] |= (1 << (k - high1 - 1)); // Добавляем старший бит
}
vcd cur(n);
for (int i = 0; i < n; i++)
cur[i] = as[rev[i]];
for (int len = 1; len < n; len <<= 1) {
vcd ncur(n);
for (int i = 0; i < n; i += len * 2)
fft_merge(cur, ncur, i, len);
cur.swap(ncur);
}
return cur;
}
Оптимизация
На многочлене степени 216 рекурсия работает 640 мс, без рекурсии — 500. Улучшение есть, но программу можно сделать еще быстрее. Воспользуемся тем свойством, что ωi=-ωi+n/2. Значит, можно не считать два раза корень и ai⋅ωj — синус, косинус и умножение комплексных чисел очень затратные операции.
fft_merge()
for (int i = 0; i < len; i++) {
double alpha = 2 * M_PI * i / nlen;
cd w = cd(cos(alpha), sin(alpha)); // Текущий корень
cd val = w * src[p2];
dest[pdest] = src[p1] + val;
dest[pdest + len] = src[p1] - val;
pdest++;
if (++p1 >= en1) p1 = start;
if (++p2 >= en2) p2 = start + len;
}
Перехо с такой оптимизацией называется «преобразованием бабочки». Программа стала работать 260 мс. Для закрепления успеха давайте предподсчитаем все корни из 1 и запишем их в массив:
fft_merge()
int rstep = roots.size() / nlen; // Шаг в массиве с корнями
for (int i = 0; i < len; i++) {
cd w = roots[i * rstep];
cd val = w * src[p2];
fft()
roots = vcd(n);
for (int i = 0; i < n; i++) {
double alpha = 2 * M_PI * i / n;
roots[i] = cd(cos(alpha), sin(alpha));
}
Теперь скорость работы — 78 мс. Оптимизация в 8 раз по сравнению с первой реализацией!
Оптимизация по коду
На данный момент весь код преобразования занимает порядка 55 строк. Не сотню, но это достаточно много — можно короче. Дляначала избавимся от кучи лишних переменных и операций в fft_merge:
void fft_merge(const vcd &src, vcd &dest, int start, int len) {
int p1 = start;
//int en1 = start + len; // Не используется, см. конец цикла
int p2 = start + len;
//int en2 = start + len * 2; // Аналогично
int pdest = start;
//int nlen = len * 2; // Используется только в следующей строчке
//int rstep = roots.size() / nlen;
int rstep = roots.size() / (len * 2);
for (int i = 0; i < len; i++) {
//cd w = roots[i * rstep]; // Также используется только в следующей строчке
//cd val = w * src[p2];
cd val = roots[i * rstep] * src[p2];
dest[pdest] = src[p1] + val;
dest[pdest + len] = src[p1] - val;
pdest++, p1++, p2++;
//if (++p1 >= en1) p1 = start; // Так как у нас теперь цикл не до 2len, а только до len, переполнения быть не может
//if (++p2 >= en2) p2 = start + len; // Убираем
}
}
Теперь можно переместить цикл из fft_merge в основную процедуру (также можно убрать p2, поскольку p2=p1+len — у меня это также дало небольшой выигрыш по времени. Что любопытно, если убрать p1=pdest, то у меня лично выигрыш по времени убивается):
fft()
for (int len = 1; len < n; len <<= 1) {
vcd ncur(n);
int rstep = roots.size() / (len * 2);
for (int pdest = 0; pdest < n;) {
int p1 = pdest;
for (int i = 0; i < len; i++) {
cd val = roots[i * rstep] * cur[p1 + len];
ncur[pdest] = cur[p1] + val;
ncur[pdest + len] = cur[p1] - val;
pdest++, p1++;
}
pdest += len;
}
cur.swap(ncur);
}
Как видите, само преобразование занимает не так много — 17 строк. Всё остальное — предподсчёт корней и разворот чисел. Если Вы готовы сэкономить код в обмен на время работы (O(n⋅log2n) вместо O(n)), можете заменить 13 строк разворота чисел на следующие шесть:
В начале процедуры fft()
vcd cur(n);
for (int i = 0; i < n; i++) {
int ri = 0;
for (int i2 = 0; i2 < k; i2++) // Перебираем биты от младших к старшим
ri = (ri << 1) | !!(i & (1 << i2)); // И приписываем в конец числа
cur[i] = as[ri];
}
В результате теперь код выглядит так:
vcd fft(const vcd &as) {
int n = as.size();
int k = 0; // Длина n в битах
while ((1 << k) < n) k++;
vector<int> rev(n);
rev[0] = 0;
int high1 = -1;
for (int i = 1; i < n; i++) {
if ((i & (i - 1)) == 0) // Проверка на степень двойки. Если i ей является, то i-1 будет состоять из кучи единиц.
high1++;
rev[i] = rev[i ^ (1 << high1)]; // Переворачиваем остаток
rev[i] |= (1 << (k - high1 - 1)); // Добавляем старший бит
}
vcd roots(n);
for (int i = 0; i < n; i++) {
double alpha = 2 * M_PI * i / n;
roots[i] = cd(cos(alpha), sin(alpha));
}
vcd cur(n);
for (int i = 0; i < n; i++)
cur[i] = as[rev[i]];
for (int len = 1; len < n; len <<= 1) {
vcd ncur(n);
int rstep = roots.size() / (len * 2);
for (int pdest = 0; pdest < n;) {
int p1 = pdest;
for (int i = 0; i < len; i++) {
cd val = roots[i * rstep] * cur[p1 + len];
ncur[pdest] = cur[p1] + val;
ncur[pdest + len] = cur[p1] - val;
pdest++, p1++;
}
pdest += len;
}
cur.swap(ncur);
}
return cur;
}
Обратное преобразование
Получить значения многочлена в точках — это, конечно, хорошо, но преобразование Фурье умеет больше — по этим значениям построить сам многочлен, причём за то же самое время! Оказывается, что если применить преобразование Фурье к массиву значений, как к коэффициентам многочлена, потом разделить результат на n и перевернуть отрезок с 1 до n-1 (нумерация с 0), то мы получим коэффициенты исходного многочлена.
Код тут предельно простой — всё уже написано. Думаю, Вы справитесь.
Доказательство
Пусть мы применяем обратное преобразование к многочлену P(x) с коэффициентами vi (исходный многочлен имел коэффициенты ai):
vi=a0+ωia1+ω2ia2+ω3ia+...
Посмотрим на результат преобразования:
bi=v0+ωiv1+ω2iv2+ω3iv3+...
Подставим значения vj (помним, что ωaωb=ωa+bmodn:
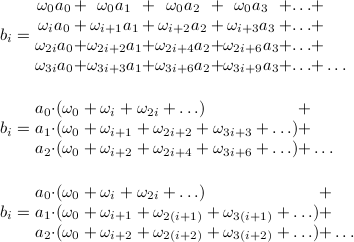
Теперь давайте докажем один замечательный факт: при x≠0, ω0+ωx+ω2x+...+ω(n-1)x=0.
Доказывается аналогично тому, что сумма корней — ноль: обозначим за φ сумму, домножим обе части на ωx и посмотрим, что получилось.
Теперь применим этот факт к вычислению значения bi. Заметим, что все строки, кроме одной, в которой содержится an-i, обнулятся.
Таким образом:
bi=an-i⋅(ω0+ω0+ω0+ω0+...)
bi=an-i⋅n
Что и требовалось доказать.
Применение
Вообще говоря, о применении я уже чуть-чуть говорил в начале статьи. В частности, теперь перемножение многочленов можно выполнять следующим образом:
Быстрое перемножение многочленов
vcd a, b; // Многочлены
// Чтение многочленов
vcd a_vals = fft(a);
vcd b_vals = fft(b);
vcd c_vals(a_vals.size());
for (int i = 0; i < a_vals.size(); i++)
c_vals[i] = a_vals[i] * b_vals[i];
vcd c = fft_rev(c_vals);
// Вывод ответа
Легко заметить, что время работы этой программы — O(n⋅log2n) и самые трудоёмкие операции — преобразования Фурье. Также можно заметить, что если нам требуется вычислить более сложное выражение с двумя многочленами, то по-прежнему можно выполнять лишь три приобразования — сложение и вычитание также будут работать за линейное время. К сожалению, с делением не всё так просто, поскольку многочлен может случайно принять значение 0 в какой-нибудь из точек. UPD2: не забудьте, что степень произведения двух многочленов степени n будет равна 2n, поэтому при вводе следует добавить «лишние» нулевые старшие коэффициенты.
Если представить число в десятичной (или более) системе счисления, как многочлен с коэффициентами — цифрами, то умножение длинных чисел также можно выполнять очень быстро.
И, напоследок, задача, которую я разберу в следующем посте: у вас есть две строки одинаковой длины порядка 105 из букв A, T, G, C. Требуется найти такой циклический сдвиг одной из строк, чтобы совпало максимальное количество символов. Очевидно наивное решение за O(n2), но есть решение при помощи БПФ.
Удачи!
UPD: Выложил код целиком на pastebin