Весьма интересный пост, опубликованный недавно на Хабре, и особенно комментарии к нему подтолкнули меня к описанию, пожалуй, единственной симметричной схемы, действительно обеспечивающей страховку от кражи базы паролей с сервера – схемы Лэмпорта («Lamport hash chain»). Алгоритм на самом деле чрезвычайно прост и предложен автором (L.Lamport) еще в 1981 году. Более того, схема в большинстве учебников уже упоминается как «устаревшая», т.к. целью ее разработки была в первую очередь защита от перехвата пароля на этапе передачи, а появившиеся позднее схемы семейства «challenge-handshake» (CHAP, CRAM) решают эту задачу гораздо более эффективно. А вот о втором интересном свойстве схемы Лэмпорта уже потихоньку забыли – она не требует конфиденциальности аутентификационных данных пользователей, хранимых на серверной стороне (свойство, обычно присущее только асимметричным схемам с сертификатам клиентов). Посмотрим, как можно достичь этого свойства с помощью одной только криптостойкой хеш-функции.
Сформулируем задачу в терминах криптографии (построим модель угроз).
A) Сервер хранит данные, позволяющие достоверно аутентифицировать клиента.
B) Раскрытие/кража этих данных не должно позволить злоумышленнику выдать себя за клиента перед сервером.
C) Раскрытие/прослушивание (в т.ч. многократное) передаваемых между клиентом и сервером данных на этапе аутентификации («прослушивание протокола») также не должно позволить злоумышленнику возможность впоследствии успешно выдать себя за этого клиента.
D) Задача защиты от активного злоумышленника-посредника («man-in-the-middle») не ставится.
E) В случае взлома сервера считаем, что злоумышленник смог нарушить только конфиденциальность, но не целостность базы аутентификационных данных (факт нарушения целостности можно отслеживать дополнительными контрольными механизмами).
Очевидно, что в случае кражи базы аутентификационных данных у злоумышленника в распоряжении оказывается ровно столько же информации, что и у сервера. А, следовательно, сам процесс проверки аутентичности клиента должен осуществляться сервером таким образом, чтобы проверить валидность клиента он мог, а самостоятельно (выступая от имени клиента) пройти ее «сам у себя» не мог. Проверкой сравнением каких-либо данных (пароля, шифрограммы и т.п.) такого свойства добиться нельзя. Проверка должна осуществляться на возможность клиента сделать что-либо такое, что не может сделать никто кроме него (в т.ч. сервер). В симметричной криптографии единственным таким преобразованием является вычисление криптостойкого хеша.
Ну а теперь собственно суть схемы.
Процесс установки аутентификационных данных
Процесс аутентификации
При каждой очередной необходимости проверки аутентичности пользователя:
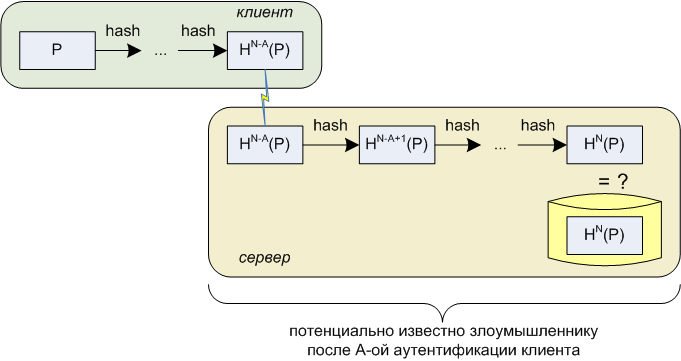
Требования B) и C) применительно к схеме Лэмпорта превращаются по сути в одно: при значении счетчика равном A злоумышленник, обладая любым набором (в т.ч., возможно, полным) значений из списка HN-A+1(P), HN-A+2(P), ..., HN(P) не должен иметь возможность успешно пройти аутентификацию ни для значения счетчика A, ни для какого либо иного значения большего A. Так ли это? Во-первых, можно заметить, что весь перечисленный выше список равнозначен по ценности для злоумышленника одному — самому первому значению HN-A+1(P) (так как остальные легко вычисляются из него). Дает ли знание HN-A+1(P) при неизвестном P возможность вычислить HN-A(P)? Без сомнения – нет, так как данная задача – это задача нахождения прообраза криптостойкой хеш-функции по известному ее значению. При достаточно большой мощности пространства входных значений эта задача по-прежнему не имеет решения в разумные сроки, несмотря на последние достижения криптоанализа хеш-функций.
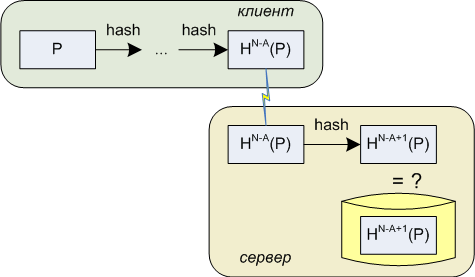
Достаточно очевидным усовершенствованием схемы, никак не влияющим на ее стойкость, является хранение на стороне сервера не значения HN(P) с постоянной проверкой из A операций, а значения HN-A+1(P) с проверкой из всего одной операции вычисления хеша: H(HN-A(P))? HN-A+1(P). Данный вариант требует обновления поля аутентификационных данных при каждом успешном входе клиента, но обновление счетчика A все равно приходится производить, поэтому отрицательного влияния здесь гораздо меньше, а положительное заключается в резком снижении нагрузки на CPU сервера, т.к. исчезает потребность в A-кратном вычислении хеша.
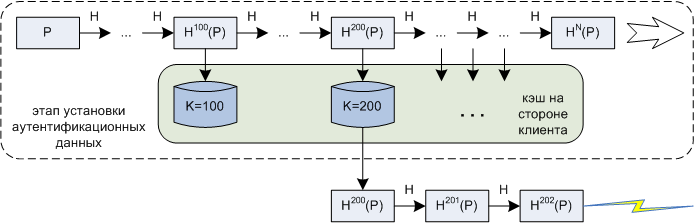
В те годы, когда схема предлагалась, вычисление тысяч значений хеш-функций считалось весьма вычислительно сложным процессом, поэтому предлагалось и усовершенствование на стороне клиента: кэширование в процессе первичного вычисления HN(P) промежуточных значений с определенным шагом. Это позволяло ускорить вычисление клиентского ответа, но требовало, как и любое кэширование, дополнительных ресурсов долговременнного хранения (причем к ним должны были предъявляться и требования конфиденциальности, аналогичные самому паролю P). В наше время вычисление 100.000 итераций хеш-функции даже на слабом ПК занимает около секунды. Поэтому подобное кэширование можно порекомендовать только для самых слабых аппаратных платформ.
Основной проблемой схемы Лэмпорта является, естественно, активный злоумышленник («man-in-the-middle»). Очевидно, что при отсутствии аутентификации сервера перед клиентом до отправки ответа злоумышленник, направив якобы от имени сервера заведомо большее чем текущее значение счетчика A’, может получить от клиента значение HN-A’(P) и вычислять после этого любого значение из диапазона HN-A’(P)… HN-A(P). Предлагаемое в некоторых источниках хранение на клиенте текущего значения счетчика A для контроля за сервером на самом деле не решает проблему, поскольку, если мы принимаем угрозу наличия злоумышленника-посредника, то он всё равно в состоянии, перехватив и подавив корректный пакет клиента HN-A(P), аутентифицироваться с его помощью уже со своей станции.
По этой же причине не имеет смысла в данной модели угроз увеличивать счетчик A при любом запросе аутентификации вне зависимости от того успешна ли она оказалась или нет, как предлагается в некоторых реализациях. Данная схема создает угрозу исчерпания (DoS) счетчика злоумышленником и при этом всё равно не защищает от злоумышленника-посредника. Сам автор в оригинальной работе не рекомендует изменять счетчик при неуспешной попытке.
Оптимальную защиту от обеих угроз на сегодняшний день может предоставить SSL (с односторонней аутентификацией сервера перед клиентом). Еще раз отмечу, что «двухсторонний» SSL с аутентификацией клиентов перед сервером своими сертификатами, конечно, решает всю проблему краж паролей в целом. Но он на порядок более тяжелый и для разворачивания и для поддержки при большом количестве клиентов. Здесь же все проблемы могут быть решены именно «односторонним» SSL с грамотно подписанным сертификатом сервера, что позволит клиенту сообщать очередные значения HK(P) только легитимному серверу.
Определенные проблемы у схемы Лэмпорта есть при восстановлении серверной системы из бэкапа в случае, если схема восстановления подразумевает RPO больше 0. В этом случае за «потерянный» период времени потенциально могли пройти успешные аутентификации клиента, подслушанные злоумышленником, а восстановленное из бэкапа значение счетчика A будет диктовать серверу снова подавать в запросе уже наблюдавшееся ранее значение A. Сам Лэмпорт предлагает в случае восстановления из резервной копии увеличивать A на среднеожидаемое количество событий аутентификаций за время нахождения системы в офф-лайне с некоторым запасом.
Переинициализация
И последняя проблема схемы: что делать, когда счетчик прошедших аутентификаций A подходит к значению N? Эта ситуация называется переинициализацией. В исходном варианте Лэмпорта переинициализация подразумевает полную перегенерацию аутентификационной информации, то есть замену P на стороне клиента и HN(P) на стороне сервере. В случае генерации P из пароля пользователя, соответственно, либо под хеш-сумму необходимо вносить кроме имени сервера еще и порядковый номер переинициализации rekey_id: P=H(password||servername||rekey_id), хранить его на сервере и сообщать клиенту в каждом запросе. Либо при каждой переинициализации изменять пароль пользователя и каким-либо образом обеспечивать полную неповторяемость паролей, что мне кажется более сложной технической задачей. Кстати, для защиты от атаки на password по известному P, переинициализацию неплохо производить как минимум за 1 шаг до N-ой аутентификации, с тем чтобы клиенту не пришлось посылать по открытому каналу значение P.
За последние 7-8 лет опубликовано сразу несколько более современных работ по самоинициализирующимся цепочкам хешей (с ними можно ознакомиться поиском по терминам «re-initializable hash chains», «infinite hash chains» или «self-updating hash chains»). Однако, хочу сказать, что математика там весьма и весьма нетривиальна, чем красота идеи Лэмперта сводится практически «на нет».
И наконец, если счетчик A увеличивается (как и в исходном варианте) только после успешной аутентификации, а клиенты обладают достаточной вычислительной мощностью, то переинициализаций можно вообще избежать, просто установив N равным, скажем, 100.000 (на 30 лет при 10 аутентификациях в сутки), что мне кажется наиболее разумным решением.
В целом схема Лэмпорта является вполне жизнеспособной и гораздо более простой в реализации альтернативой асимметричной аутентификации клиентов, несколько необоснованно забытой в наши дни.
Формализованное описание задачи
Сформулируем задачу в терминах криптографии (построим модель угроз).
A) Сервер хранит данные, позволяющие достоверно аутентифицировать клиента.
B) Раскрытие/кража этих данных не должно позволить злоумышленнику выдать себя за клиента перед сервером.
C) Раскрытие/прослушивание (в т.ч. многократное) передаваемых между клиентом и сервером данных на этапе аутентификации («прослушивание протокола») также не должно позволить злоумышленнику возможность впоследствии успешно выдать себя за этого клиента.
D) Задача защиты от активного злоумышленника-посредника («man-in-the-middle») не ставится.
E) В случае взлома сервера считаем, что злоумышленник смог нарушить только конфиденциальность, но не целостность базы аутентификационных данных (факт нарушения целостности можно отслеживать дополнительными контрольными механизмами).
Основная идея метода
Очевидно, что в случае кражи базы аутентификационных данных у злоумышленника в распоряжении оказывается ровно столько же информации, что и у сервера. А, следовательно, сам процесс проверки аутентичности клиента должен осуществляться сервером таким образом, чтобы проверить валидность клиента он мог, а самостоятельно (выступая от имени клиента) пройти ее «сам у себя» не мог. Проверкой сравнением каких-либо данных (пароля, шифрограммы и т.п.) такого свойства добиться нельзя. Проверка должна осуществляться на возможность клиента сделать что-либо такое, что не может сделать никто кроме него (в т.ч. сервер). В симметричной криптографии единственным таким преобразованием является вычисление криптостойкого хеша.
Ну а теперь собственно суть схемы.
Процесс установки аутентификационных данных
- Клиент и сервер договариваются о числе N (из диапазона, скажем от 1.000 до 100.000) – эта величина несекретна и может быть просто hard-coded.
- Клиент выбирает случайное число P большой размерности (128 бит и более):
— либо вычисляет его с помощью хеш-функции из пароля пользователя и имени сервера P=H(password||servername);
— либо генерирует его из доверенных источников случайных/псевдослучайных чисел и сохраняет на своей стороне (недостатком является появляющаяся при этом «привязка» к клиентской станции или необходимость использования токенов). - Клиент выполняет N раз рекурсивно криптостойкое хеширование H над числом P и передает получившийся результат H(H(H(...H(P)))) = HN(P) по любому каналу, защищенному от модификации, на сервер (Внимание! Запись HK(P) в течение всей статьи будет использоваться для обозначения суперпозиции (K-кратного повторения вызова) хеш-функции, а не возведения ее результата в степень K).
- Сервер инициализирует счетчик A порядкового номера предстоящей аутентификации клиента числом 1.
Процесс аутентификации
При каждой очередной необходимости проверки аутентичности пользователя:
- Сервер высылает претенденту число A.
- Клиент выполняет (N-A) раз хеширование над числом P и передает получившийся результат HN-A(P) серверу.
- Сервер производит над числом HN-A(P) еще A раз хеширование и сверяет получившийся результат HA(HN-A(P)) с хранящимся у него HN(P).
- При совпадении результата клиент считается успешно подтвердившим свою аутентичность, а сервер увеличивает счетчик успешных аутентификаций на 1: A=A+1, «сдвигаясь» тем самым по цепочке на одну позицию влево.

Доказательство наличия требуемых свойств
Требования B) и C) применительно к схеме Лэмпорта превращаются по сути в одно: при значении счетчика равном A злоумышленник, обладая любым набором (в т.ч., возможно, полным) значений из списка HN-A+1(P), HN-A+2(P), ..., HN(P) не должен иметь возможность успешно пройти аутентификацию ни для значения счетчика A, ни для какого либо иного значения большего A. Так ли это? Во-первых, можно заметить, что весь перечисленный выше список равнозначен по ценности для злоумышленника одному — самому первому значению HN-A+1(P) (так как остальные легко вычисляются из него). Дает ли знание HN-A+1(P) при неизвестном P возможность вычислить HN-A(P)? Без сомнения – нет, так как данная задача – это задача нахождения прообраза криптостойкой хеш-функции по известному ее значению. При достаточно большой мощности пространства входных значений эта задача по-прежнему не имеет решения в разумные сроки, несмотря на последние достижения криптоанализа хеш-функций.
Эффективная реализация
Достаточно очевидным усовершенствованием схемы, никак не влияющим на ее стойкость, является хранение на стороне сервера не значения HN(P) с постоянной проверкой из A операций, а значения HN-A+1(P) с проверкой из всего одной операции вычисления хеша: H(HN-A(P))? HN-A+1(P). Данный вариант требует обновления поля аутентификационных данных при каждом успешном входе клиента, но обновление счетчика A все равно приходится производить, поэтому отрицательного влияния здесь гораздо меньше, а положительное заключается в резком снижении нагрузки на CPU сервера, т.к. исчезает потребность в A-кратном вычислении хеша.

В те годы, когда схема предлагалась, вычисление тысяч значений хеш-функций считалось весьма вычислительно сложным процессом, поэтому предлагалось и усовершенствование на стороне клиента: кэширование в процессе первичного вычисления HN(P) промежуточных значений с определенным шагом. Это позволяло ускорить вычисление клиентского ответа, но требовало, как и любое кэширование, дополнительных ресурсов долговременнного хранения (причем к ним должны были предъявляться и требования конфиденциальности, аналогичные самому паролю P). В наше время вычисление 100.000 итераций хеш-функции даже на слабом ПК занимает около секунды. Поэтому подобное кэширование можно порекомендовать только для самых слабых аппаратных платформ.

Вопросы, проблемы и пути их решения
Основной проблемой схемы Лэмпорта является, естественно, активный злоумышленник («man-in-the-middle»). Очевидно, что при отсутствии аутентификации сервера перед клиентом до отправки ответа злоумышленник, направив якобы от имени сервера заведомо большее чем текущее значение счетчика A’, может получить от клиента значение HN-A’(P) и вычислять после этого любого значение из диапазона HN-A’(P)… HN-A(P). Предлагаемое в некоторых источниках хранение на клиенте текущего значения счетчика A для контроля за сервером на самом деле не решает проблему, поскольку, если мы принимаем угрозу наличия злоумышленника-посредника, то он всё равно в состоянии, перехватив и подавив корректный пакет клиента HN-A(P), аутентифицироваться с его помощью уже со своей станции.
По этой же причине не имеет смысла в данной модели угроз увеличивать счетчик A при любом запросе аутентификации вне зависимости от того успешна ли она оказалась или нет, как предлагается в некоторых реализациях. Данная схема создает угрозу исчерпания (DoS) счетчика злоумышленником и при этом всё равно не защищает от злоумышленника-посредника. Сам автор в оригинальной работе не рекомендует изменять счетчик при неуспешной попытке.
Оптимальную защиту от обеих угроз на сегодняшний день может предоставить SSL (с односторонней аутентификацией сервера перед клиентом). Еще раз отмечу, что «двухсторонний» SSL с аутентификацией клиентов перед сервером своими сертификатами, конечно, решает всю проблему краж паролей в целом. Но он на порядок более тяжелый и для разворачивания и для поддержки при большом количестве клиентов. Здесь же все проблемы могут быть решены именно «односторонним» SSL с грамотно подписанным сертификатом сервера, что позволит клиенту сообщать очередные значения HK(P) только легитимному серверу.
Определенные проблемы у схемы Лэмпорта есть при восстановлении серверной системы из бэкапа в случае, если схема восстановления подразумевает RPO больше 0. В этом случае за «потерянный» период времени потенциально могли пройти успешные аутентификации клиента, подслушанные злоумышленником, а восстановленное из бэкапа значение счетчика A будет диктовать серверу снова подавать в запросе уже наблюдавшееся ранее значение A. Сам Лэмпорт предлагает в случае восстановления из резервной копии увеличивать A на среднеожидаемое количество событий аутентификаций за время нахождения системы в офф-лайне с некоторым запасом.
Переинициализация
И последняя проблема схемы: что делать, когда счетчик прошедших аутентификаций A подходит к значению N? Эта ситуация называется переинициализацией. В исходном варианте Лэмпорта переинициализация подразумевает полную перегенерацию аутентификационной информации, то есть замену P на стороне клиента и HN(P) на стороне сервере. В случае генерации P из пароля пользователя, соответственно, либо под хеш-сумму необходимо вносить кроме имени сервера еще и порядковый номер переинициализации rekey_id: P=H(password||servername||rekey_id), хранить его на сервере и сообщать клиенту в каждом запросе. Либо при каждой переинициализации изменять пароль пользователя и каким-либо образом обеспечивать полную неповторяемость паролей, что мне кажется более сложной технической задачей. Кстати, для защиты от атаки на password по известному P, переинициализацию неплохо производить как минимум за 1 шаг до N-ой аутентификации, с тем чтобы клиенту не пришлось посылать по открытому каналу значение P.
За последние 7-8 лет опубликовано сразу несколько более современных работ по самоинициализирующимся цепочкам хешей (с ними можно ознакомиться поиском по терминам «re-initializable hash chains», «infinite hash chains» или «self-updating hash chains»). Однако, хочу сказать, что математика там весьма и весьма нетривиальна, чем красота идеи Лэмперта сводится практически «на нет».
И наконец, если счетчик A увеличивается (как и в исходном варианте) только после успешной аутентификации, а клиенты обладают достаточной вычислительной мощностью, то переинициализаций можно вообще избежать, просто установив N равным, скажем, 100.000 (на 30 лет при 10 аутентификациях в сутки), что мне кажется наиболее разумным решением.
В целом схема Лэмпорта является вполне жизнеспособной и гораздо более простой в реализации альтернативой асимметричной аутентификации клиентов, несколько необоснованно забытой в наши дни.