Предисловие
Это приложение может и не имело практической ценности, но опыта прибавило действительно много. Я бы хотел немного поразмышлять на тему компьютерного зрения. Эта область является одной из самых захватывающих в современных компьютерных вычислениях, и она очень сложна. Что легко и просто для человеческого мозга, то очень сложно для компьютера. Многие вещи до сих пор остаются невозможными с сегодняшним уровнем развития IT.
Программа написана с помощью низкоуровневого языка C++, потому что я действительно хотел понять, как же это все работает изнутри. Если вы тоже хотите начать изучение компьютерного зрения, то для этого пригодиться библиотека OpenCV. На CodeProject вы сможете найти несколько уроков по ней. Изображение с веб-камеры получается с помощью исходного кода Вадима Горбатенко (AviCap CodeProject).
Изображение ниже объясняет принцип работы программы.
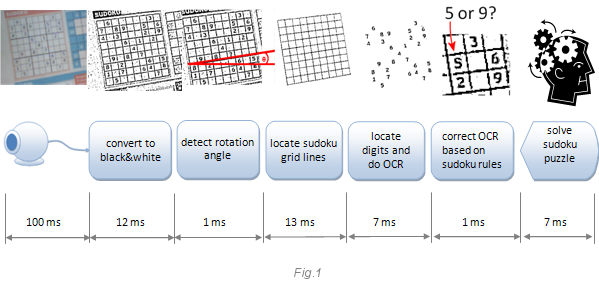
Временные интервалы внизу – задержки в миллисекундах на моём 2.8 GHz ПК с разрешением веб-камеры 640x480. Мы наблюдаем интересный результат. Например, самый медленный шаг – это получение кадра с камеры. Он занимает 100 мс, и это означает, что вы будете получать всего 10 кадров в секунду. Это мало. Веб-камеры, как правило, медленные. Вы можете ускорить их, сменив разрешение. Уменьшив его, вы ускорите съёмку, но пожертвуете качеством, и оно может стать абсолютно непригодным для анализа. Другой сюрприз заключается в том, что конвертация изображения в бинарный вид (только белый или чёрный) также занимает много времени, целых 12 мс. С другой стороны, я ожидал, что корректировка OCR и решение самой судоку будет занимать много времени, и был приятно удивлён, когда оказалось, что эти шаги выполняются вместе за 8 мс. Ниже я объясню каждый шаг детально и покажу, что можно улучшить.
Как работает конвертация в монохромное изображение
Выбор порога
Каждое приложение с компьютерным зрением начинает с конвертации цветного (или чёрно-белого) изображения в монохромное. В будущем, возможно, будет какой-то алгоритм, который будет использовать цвета, но сегодня приложения компьютерного зрения работают с монохромными изображениями (они дальтоники).
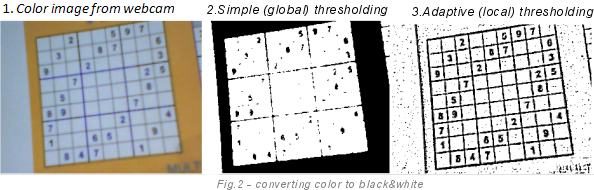
Самый простой метод для конвертации изображения – это общий порог. Предположим, что у вас есть пиксель с цветом RGB (200, 200, 200). Так как интенсивность компонент изменяется от 0 до 255, то пиксель очень яркий. Выбрав порог, как половину интенсивности: 256/2=128, мы получим, что наш пиксель должен стать белым. Но общий порог редко используется в настоящих приложениях, так как он малополезен. Куда более полезен алгоритм локального порога.
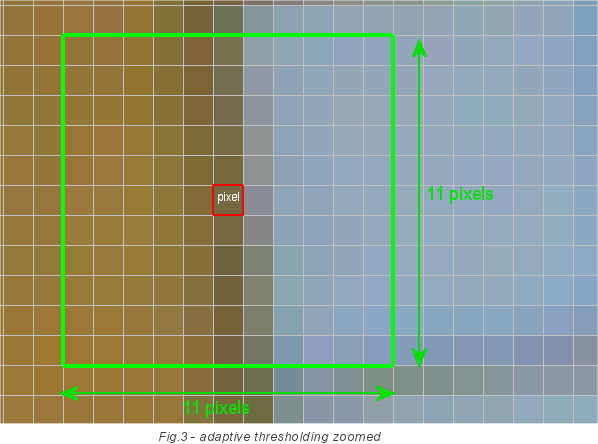
Для правильной конвертации изображения в монохромное, мы будем использовать адаптивный выбор порога. Он не использует фиксированное значение порога в 128. Вместо этого, он считает порог для каждого пикселя отдельно. Он берёт квадрат со стороной в 11 пикселей и с центром в нашем пикселе и суммирует интенсивность всех точек. Среднее значение интенсивности и будет являться порогом для данного пикселя. Формула интенсивности для текущего пикселя: порог=сумма/121, где 121=11х11. Если интенсивность нашего пикселя выше порогового значения, то он конвертируется в белый, если же нет, то в чёрный. На изображении ниже пиксель, для которого определяется порог, отмечен красным. И эти подсчёты производятся для каждого пикселя. Поэтому данный шаг является таким медленным, ведь алгоритм требует ширина*высоты*121 чтений пикселя изображения.
Целочисленная форма
Этот шаг может быть оптимизирован с помощью использования «Целочисленной формы». Целочисленная форма – это массив целых чисел с размерами изображения. Смысл гениален и прост. Возьмём изображение. Допустим у нас есть область 12х12, где интенсивность пикселей равна 1 (в реальном мире так не бывает, ведь никогда не бывает так просто), целочисленный образ – это сумма всех пикселей с левого верхнего до текущего (правого нижнего).

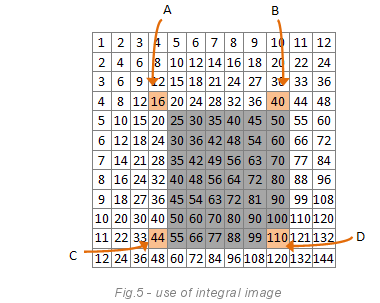
Следующее изображение демонстрирует, чем может быть полезен целочисленный образ. Целью является посчитать сумму пикселей в сером прямоугольнике.
Формула: сумма=D-C-B+A. В нашем случае: 110-44-40+16=42 (попробуйте посчитать вручную).
Вместо чтения всех пикселей из серого прямоугольника (который может быть намного больше, чем в примере), нам необходимо всего лишь одно чтение памяти. Это значительная оптимизация алгоритма. Но даже с ней, конвертация изображения в монохромное является очень тяжёлой.
Как определить угол поворота
Веб-камера не сканер. И картинка никогда не будет идеально ровно, а значит в порядке вещей немного скошенное и повёрнутое изображение. Чтобы определить угол поворота, мы будем пользоваться фактом, что изображение с судоку всегда имеет горизонтальные и вертикальные линии. Мы будем определять самые выразительные и жирные линии рядом с центром изображения. Самые выразительные линии не подвержены зашумлению. Алгоритм нахождения монохромных линий на изображении называется преобразованием Хафа.
Как это работает? Вы должны вспомнить школьную формулу y=(x*cos(theta)+rho)/sin(theta).
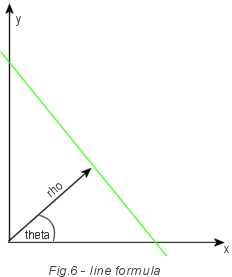
Где theta –угол линии, а rho является расстоянием от линии до центра координат (0, 0).
Важным является то, что линия может быть описана всего двумя переменными: углом наклона и расстоянием до центра координат.
Алгоритм проходит по всем пикселям в монохромном изображении, пропуская белые пиксели. Когда он попал на чёрный пиксель, то пытается «нарисовать» всевозможные линии, проходящие через этот пиксель с шагом в 1 градус. Это означает, что каждый пиксель имеет 180 воображаемых линий, проходящих через него. Почему не 360? Да потому что углы 180-360 являются копиями линий с углами 0-180 градусов.
Это множество воображаемых линий называется накопителем, двумерным массивом с размерностями theta и rho, которые были в формуле выше. Каждая воображаемая линия представлена одним значением в накопителе. Кстати, метод называется преобразованием, потому что он преобразовывает линии из (x, y) в массив (theta, tho). Каждая воображаемая линия добавляет значение в накопитель, повышая вероятность того, что воображаемая линия совпадает с реальной. Это как голосование. Настоящие линии имеют больше всего «голосов».
После того, как все пиксели и их 180 воображаемых линий «проголосовали», мы должны найти максимальное значение в накопителе. (Кстати, накопителем он называется потому что накапливает голоса) Победителем голосования является самая выразительная линия. Её параметра theta и rho могут использоваться с помощью формулы выше чтобы нарисовать её.
На следующем изображении приведён небольшой пример. Слева мы имеем линию, состоящую из трёх пикселей. Вы точно знаете, что это диагональная линия слева направо, но для компьютера это не так очевидно.
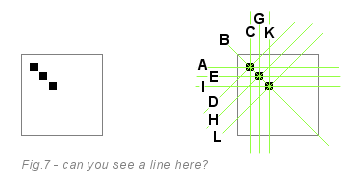
Посмотрев на это изображение, можно понять, как же работает обнаружение линий. Алгоритм преобразования Хафа пропускает белые пиксели. На каждом чёрном пикселе он рисует четыре воображаемых зелёных линии (на самом деле их 180, но для простоты мы возьмём четыре), проходящие через текущий пиксель. Первый пиксель голосует за линии A, B, C и D. Второй пиксель голосует за линии E, B, G, H. Третий за I, B, K, L. За линию B проголосовали все три пикселя, а остальные линии получили всего по одному голосу. Таким образом, линия B победила в голосовании.
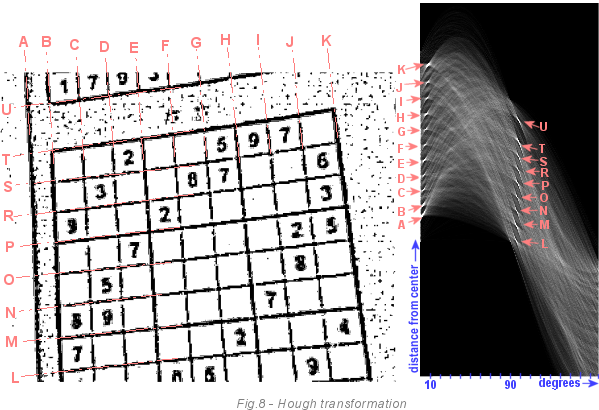
Следующее изображение является более сложным примером. Слева мы видим сетку судоку, а справа массив накопителя после прохождения по изображению алгоритма преобразования Хафа. Яркие светлые области являются линиями, которые получили много голосов. Темнота означает, что у нас нет шанса найти линию с такими параметрами на изображении. Сконцентрируемся только на ярких точках. Каждая линия (A-U) имеет яркую точку в накопителе. Вы можете видеть, что все линии слегка повёрнуты (примерно на 6 градусов). Линия A меньше повёрнута, чем линия К. Потому что изображение не только повёрнуто, но и скошено. Также, если вы посмотрите внимательнее, то увидите, что линии А и В ближе друг к другу, чем В и С. Это можно заметить на обоих изображениях.
Преобразование Хафа важно понять, если вы хотите заниматься распознаванием образов. Концепция виртуальных линий, которые могут быть реальными с помощью голосования, может быть распространена на любую геометрическую фигуру. Линия – простейшая из них, поэтому является самой простой для понимания.
Если вам надо найти окружность, то понадобится накопитель с тремя размерностями: x, y и r. Где x и y являются координатами центра нашей окружности, а r радиусом.
Преобразование Хафа может быть оптимизировано ограничением области и возможных углов исходного изображения. Нам не надо анализировать все линии, только те, что близки к центру. В нашем случае, именно от них мы и можем отталкиваться.
Как определить сетку
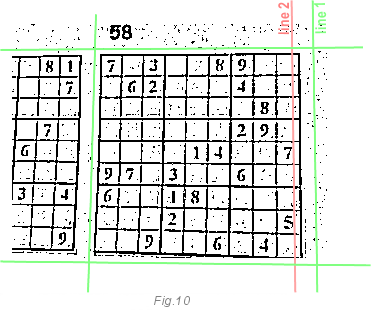
Для получения чисел из сетки судоку, нам надо определить, а где же наша сетка начинается и кончается. Эта часть является простейшей частью для человеческого мозга, но самой сложной для компьютера. Почему? Почему бы не использовать линии, найденные с помощью преобразования Хафа в предыдущем шаге? В них слишком много лишних данных. Очень часто газеты и журналы печатают несколько судоку рядом (хм, они явно не рассчитывают на компьютерное распознавание последних). На изображении будет слишком много лишних линий. Например, посмотрите на изображение ниже:

Компьютеру очень сложно определить, какие линии относятся к необходимым нам, а какие являются всего лишь информационным шумом. Где конец нашей сетки и начало следующей.
Чтобы решить эту проблему, мы не будем определять чёрные линии. Вместо этого, мы будем определять белые области вокруг сетки. На следующем изображении, вы можете увидеть это. Зелёная линия 1 никогда не пересекается с чёрными пикселями в то время, как линия 2 делает это 10 раз. Это означает, что за сеткой скорее находится линия 1, нежели линия 2. Просто подсчитав, сколько раз зелёная линия пересекает чёрные пиксели, мы можем сделать вывод, что она находится за границей сетки. Достаточно просто подсчитать как много переходов с белого на чёрный пиксель под линией. Кстати, вам не надо пробегаться по каждой линии, достаточно выполнять эти действия каждую третью линию для увеличения скорости выполнения.
После того, как мы определили границы, запустим алгоритм преобразования Хафа чтобы точно определить линии сетки. До сих пор мы не заботились о перекосах и других дефектах изображения. Только об угле поворота. Этот шаг исправит это. Путём запуска преобразования Хафа, мы получим точные положения линий сетки. Это поможет определить числа в сетке.
TODO: Этот шаг может быть более устойчивым к шуму. В следующей версии я планирую комбинировать текущий метод с Хаара-подобными алгоритмами для определения углов сетки. Я надеюсь, это увеличит качество. Проблема может быть в том, что метод с Хаара-подобными алгоритмами хорошо работает со сплошными областями, а не с линиями. Линии занимают маленькую площадь, поэтому разница между светлым и тёмным прямоугольником не так уж и велика.
Интересно, что будет при попытке обнаружения сетки 10х10…
Как работает OCR
После того, как мы определили, где должны находиться числа, нам необходимо распознать их. Это относительно легко. В алфавите только цифры от 1 до 9.
Теория
Каждый алгоритм распознавания имеет три шага:
- Определение необходимых признаков
- Тренировка
- Классификация (распознавание в рантайме)
Определение необходимых признаков является частью разработки приложения. Например, цифра один тонкая и высокая. Именно это и отличает её от остальных. Цифра 8 имеет две окружности, в верхней половине и в нижней, и т. д.
Определение необходимых признаков может быть трудной и не интуитивной работой, в зависимости от того, что надо распознать. Например, что необходимо для распознавания чьего-то лица? Не любого, а какого-то конкретного.
Зоны
В нашем приложении был использован способ плотности зон. Следующим шагом (Это должно быть сделано заранее) является тренировка приложения на цифры от 1 до 9. Вы можете найти эти изображения в каталоге ./res. Они уменьшены до размера 5х5, нормализованы и хранятся в статическом массиве OCRDigit::m_zon[10][5][5], который выглядит примерно так:

Уменьшение до размеров 5х5 называется зоннированием или разбивкой на зоны. Массив выше называется плотностью функции.
Нормализация значит, что плотность варьируется от 0 до 1024. Без нормализации зоны нельзя сравнивать корректно.
Что происходит во время выполнения программы: когда цифра получена из исходного изображения, она уменьшается до размера 5х5. После этого каждый её пиксель сравнивается с каждым пикселем из девяти цифр из тренированного массива. Целью является найти цифру с минимальным различием.
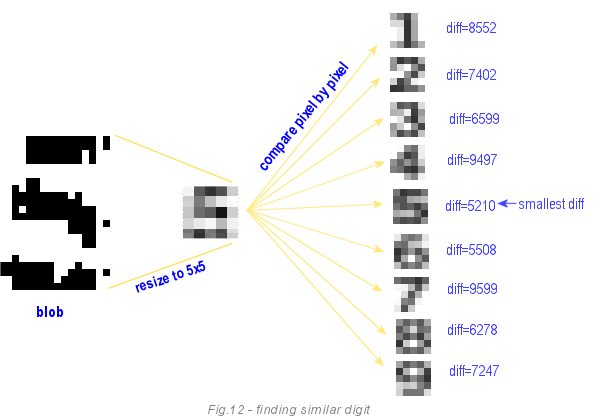
Этот метод инвариантен к размеру изображения, так как в любом случае мы используем зоны 5х5. Он чувствителен к поворотам, но мы уже позаботились об этом раньше. Проблема в том, что он чувствителен к позиции и смещению, а также не работает с негативами (белым по чёрному) и перевёрнутыми вверх тормашками цифрами.
Соотношение ширина/высота
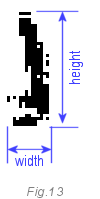
Цифра один является частным случаем. Так как она похожа на 4 и 7, то метод определения, данный выше, может оказаться ненадёжным. Специфичный параметр единицы: в нашем случае, её ширина на 40% меньше, чем высота. Нет другой такой цифры с таким же соотношением. У нас уже есть 25 зон (признаков), так вот это является 26-м признаком.
TODO: В следующей версии, качество OCR может быть улучшено введением новых признаков. Например, цифры 5,6 и 9 очень похожи при использовании разбиения на зоны. Для того, чтобы различать их, мы можем использовать их профили как признаки. Особенностью признака является количество пикселей (расстояние) между краем рамки цифры и её границей.
На изображении ниже, вы можете видеть, что профили цифр 5 и 6 похожи, но они отличаются от профиля 9. Левый профиль 5 и 9 похож, но отличается от профиля 6.

Можно добавить ещё несколько усовершенствований. Профессиональные OCR движки используют много признаков. Некоторые из них очень экзотические.
Корректировка результатов OCR
Как только OCR закончен, результаты корректируются в соответствии с правилами судоку. В одной строке, столбце и блоке 3х3 не может находиться одна и та же цифра. Если правило нарушено, то необходимо ввести коррективы в полученные результаты. Мы заменим неправильную цифру той, что возможна из оставшихся. Например, в изображении 12 выше, результат 5 потому что diff=5210, которое является самым маленьким значением различия. Следующий возможный результат 6, так как diff=5508 в этом случае. Таким образом, мы заменим 5 на 6. Чтобы решить, которая из двух цифр неверная, мы сравним значения их различий с их образцами, и та, у которой значение меньше, будет считаться верной. Исходный код корректировки вы можете найти в функции SudSolver::Fixit();
Как работает функция решения судоку
Существует несколько способов решения судоку. Мы используем три простых метода, которые работают вместе и дополняют друг друга: открытые цифры, скрытые цифры и перебор.
Перебор
Это самый широко используемый программистами способ, который точно даёт решение независимо от уровня сложности. Но перебор может быть очень долгим, это зависит от глубины рекурсии. Вы никогда не узнаете, сколько же итераций вам понадобиться. Во время перебора в клетку ставятся поочерёдно возможные из значений от 1 до 9 и продолжается решение судоку с поставленным числом. Если мы зашли в тупик (получили в одной строке/столбце/блоке одинаковые цифры, то меняем цифру на следующую). На самом деле, может быть больше одного решения, но будет круто, если мы найдём хотя бы одно. (У переводчика был в решении именно перебор и работал он на удивление быстро).
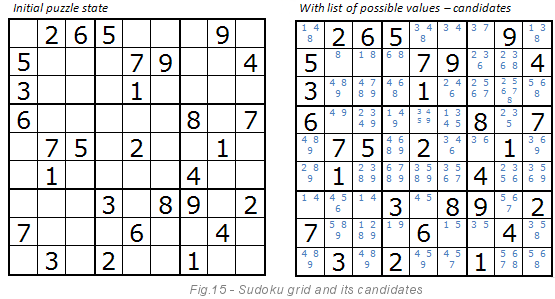
Во-первых, необходимо подготовить таблицу кандидатов – возможных значений для каждой пустой клетки. Изображение ниже объясняет, что именно такое кандидаты. Они окрашены в синий цвет. По правилам судоку, первая клетка может содержать только цифры 1, 4, 8. Тройка не может там находиться, так как она есть уже двумя клетками ниже.
Метод перебора пробует скомбинировать все синие цифры пока не найдёт решения. Посмотрим на первую клетку. Алгоритм начитается с единицы, в пятой клетке будет значение 3 и т. д. Если какая-то цифра не согласуется с другими значениями, то алгоритм пробует другую. Например, шестая клетка слева также имеет цифру 3 в качестве кандидата, но это не согласуется с пятой клеткой, поэтому алгоритм попробует следующую цифру, то есть 4 и т.д.
Перебор может быть очень медленным, если решение требует много итераций. Например, следующее изображение это очень плохой случай для нашего алгоритма. Начиная с левой верхней клетки будет слишком много переборов, но есть и хорошие новости: начинайте с клетки, где вариантов поменьше. Это ускорит решение.

Есть ещё несколько оптимизаций для увеличения производительности алгоритма, таких как сортировка рекурсивной последовательности от клеток с наименьшим количеством кандидатов к клеткам с наибольшим. Но мы не используем этот алгоритм, так как это только частичная оптимизация. Все судоку имеют плохие клетки, и обрабатываются не столь быстро для приложений в реальном времени.
Открытые цифры
Изображение ниже объясняет этот метод. Если ячейка имеет единственного кандидата, то мы с уверенностью можем сказать, что именно эта цифра должна стоять в этой клетке. После установки значения, следующим шагом будет перестроить список кандидатов. Список кандидатов уменьшается, пока существуют одиночные кандидаты. Это очевидный и простой метод для компьютеров. Но не такой очевидный для людей, как мне кажется. Живые игроки не могут хранить список кандидатов в голове и постоянно его перестраивать и корректировать.
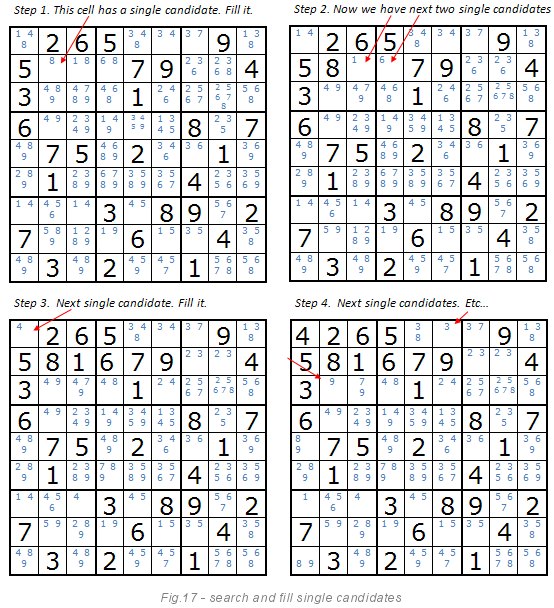
Скрытые цифры
Как и раньше, изображение ниже объясняет этот метод. Посмотрите на цифру 7.Если вы разгадываете судоку, то скорее всего скажете, что семёрка должна быть именно в указанной клетке.
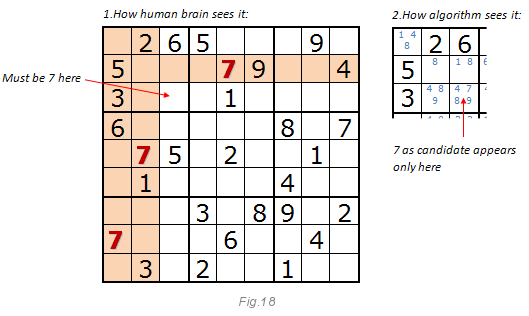
Даже если эта клетка имеет четырёх кандидатов: 4, 7, 8, 9 (см. рис. 15), фокус в том, что мы ищем уникальные цифры из кандидатов в блоке 3х3, в строке и в столбце. Метод, возможно, сможет решить весь пазл целиком, но лучше работает с методом 2. Когда в методе открытых цифр кончаются одиночные кандидаты, на сцену выходит метод скрытых цифр.
Комбинирование всех методов вместе
Для на важна скорость обработки и решения. Перебор не слишком быстрый метод. Таким образом, мы будем использовать комбинацию всех трёх методов. Методы 2 и 3 очень быстрые, но могут решать только быстрые пазлы. Так как мы просим приложение решить пазл за нас, то это значит, что он действительно сложный. Ниже приведён алгоритм работы. С левой стороны расположены быстрые методы 2 и 3. И только если им не удаётся решить пазл, управление переходит правой стороне с методом перебора, уменьшив работу для этого алгоритма.
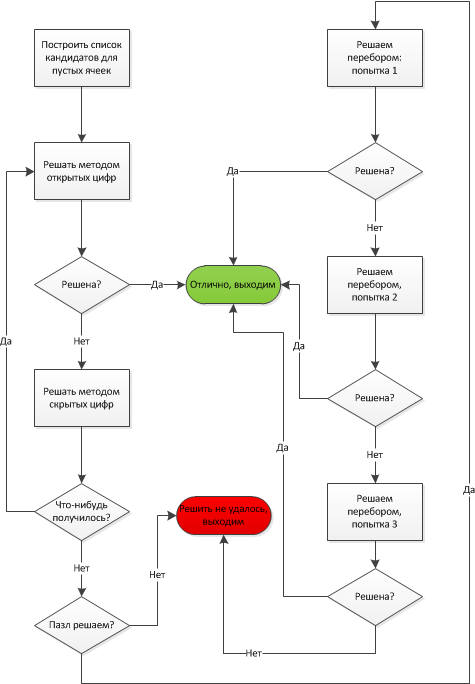
Только если методы 2 и 3 не могут решить пазл, программа начинает передирать значения. И даже тогда, алгоритм перебора ограничен по времени 600000 итерациями. Также существует три попытки, после чего программа сдаётся. Между каждой попыткой, рекурсивная последовательность переставляется случайным образом с надеждой, что новая последовательность поможет решить пазл быстрее. Если мы решить судоку так и не смогли, то может нам повезёт на следующем кадре камеры. Представленная блок-схема описана в функции SudSolver::SolveMe().
Буфферизация решения
Когда решение найдено, мы сохраняем его в массиве типа SudResultVoter. Буфферизация необходима, потому что OCR не на 100% гарантирует правильность результата, и время от времени мы получаем разные решения. Чтобы избежать неустойчивого решения, мы всегда будем показывать сильнейшее (для точности 12 последних решений). Время от времени массив обнуляется, забывая старые решения и давая шанс новым.
Видео
TODO:
Некоторые идеи на будущее:
- Переписать программу под Android. Мне интересно, как это будет работать на смартфонах
- Распараллелить некоторые функции на многопроцессорных системах. Сегодня большинство ПК имеют минимум два ядра. Обычно, распараллеливание даёт прирост производительности. Но с решаталем через веб-камеру нам нужна не столько скорость, сколько точность и качество. По идее, распараллеливание задач должны улучшить операции над похожими кадрами, но с различными настройками. После того, как все задачи будут закончены, мы просто возьмём лучший результат.
Скачать демо — 170 KB
Скачать исходники — 307 KB
Также есть зеркало исходников на GitHub: github.com/NeonMercury/Realtime-Webcam-Sudoku-Solver