Попробуем проверить гипотезу о том, являются ли приращения значений индекса DJI статистически независимыми. При этом в качестве референсного источника данных, с которым будем проводить сравнение, возьмем искусственный временной ряд, сгенерированный из собственно приращений исходного ряда, но при этом случайно перемешанных. В качестве меры статистической независимости воспользуемся статистикой взаимной информации.
В качестве подопытного источника данных возьмем данные DJI за 30 лет (дневные цены закрытия), с 1981-08-31 по 2011-08-26 (Источник: finance.yahoo.com).
Значения индекса Dow Jones Industrial Average (DJI)

Ряд процентных приращений котировок, расчитанный по формуле X[t] / X[t-1] — 1

Для приведения исследуемой непрерывной, по ее сути, переменной к дискретному типу перейдем к ряду процентных приращений, округленных до 0,01 (1%). Подсчет взаимной информации для непрерывных переменных, хотя и возможен технически, но не информативен, в силу очень большого значения n — конечного набора значений признака, принимаемого случайной переменной.

(Все формулы а также теория заимствованы в: ru.wikipedia.org а также из ряда монографий, которые можно поискать по ключевым словам.)
Теория информация развивалась неразрывно с теорией связи, я не буду отходить от этой традиции.
Представим, что есть некий передатчик и приемник данных. Передатчик передает дискретную переменную X, которая принимает ограниченное количество возможных вариантов значений x (это также называется алфавит). Вероятность реализации каждого конкретного значения отличается от нуля, иначе такое значение просто исключается из анализа. Вид функции плотности вероятности на пространстве значений, принимаемых переменной, может быть произвольным. Сумма всех вероятностей по каждому возможному значению равна 1 (если сумма равна 0, то дальнейший ход мыслей не имеет смысла).
Приемник воспринимает передаваемые значения X, или можно сказать, что в точке приема значений осуществляется событие — переменная X приняла значени�� x. И чем меньше мы, то есть, наблюдатели, знаем о том, какое именно событие произойдет (сиречь, какое именно значение примет приемник), тем большей энтропией обладает данная система, и, тем больше информации принесет с собой осуществление этого события.
Значит, информационная энтропия (понятия, заимствованное из энтропии в теоретической физики) это количественная мера неопределенности в абстрактной системе состоящей из возможности реализации события и его непосредственной реализации. Мда, звучит, действительно, абстрактно. Но в этом и сила этой теории: она может применяться к широчайшему классу явлений.
А все же, что такое информация? Это также количественная мера, характеризующая количество энтропии, или неопределенности, которое ушло из системы при реализации конкретного события. Информация, следовательно, количественно равна энтропии.
Если говорят про весь спектр значений, которые реализуются в системе, то говорят про среднюю информацию или информационную энтропию. Эта величина считается по формуле:

Если говорят про информацию отдельно взятой реализации случайной величины, говорят про собственную информацию:

Например, опыт с многократным подкидыванием честной монетки — это система со средней информацией равной 1 Бит (при подстановке в формулу логарифма по основанию 2). При этом, перед каждым подбрасыванием мы ожидаем выпадение решки или орла с равной вероятностью (эти события! независимы! друг от друга) и неопределенность всегда равна 1. А какова будет информационная энтропия этой системы при неравной вероятности выпадения сторон монетки? Скажем, орел выпадает с вероятностью 0,6, а решка — с вероятностью 0,4. Посчитаем и получим: 0,971 Бита. Энтропия системы уменьшилась, так как неопределенность реализации эксперимента уже меньше: мы ожидаем орел чаще, чем решку.
Возвращаясь к примеру с передатчиком и приемником, если связь между ними идеально хорошая, то информация (в широком смысле) будет всегда передаваться на 100% правильно. Иначе говоря, взаимная информация между передатчиком и приемником будет равна средней информации самого приемника (символизирующего реализацию события), а если данные из передатчика будут никак не связаны с данными, получаемым приемником, то взаимная информация между ними будет равна 0. Иначе говоря, то что передает передатчик ничего не говорит о том, что принимает приемник. Если есть некоторые потери информации, то взаимная информация будет величиной от 0 до средней информации приемника.
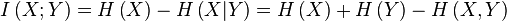
В контексте задачи, о которой я писал в этой статье, взаимная информация выступает инструментом нахождения произвольного вида зависимости между приемником (зависимой переменной) и передатчиком (независимой переменной). Максимизация взаимной информации между парой переменных указывает на наличие некоторой детерминированности реализации случайного значения по отношению к его прошлым реализациям. Можно, конечно, в качестве независимых переменных взять что угодно, от состава поющих птиц по утрам, до частоты определенных слов в интернет-публикациях на тему биржевой торговли. «Истина где-то рядом.»
Итак, посчитаем энтропию источника данных (http://ru.wikipedia.org/):

Средняя информация (или просто энтропия) данного источника данных (посчитанная по логарифму с основанием 2) составляет 2.098 Бит.
Взаимная информация между случайными переменными посчитана через понятие информационной энтропии (http://ru.wikipedia.org/):
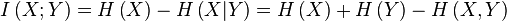
Гистограмма значений взаимной информации между зависимой переменной — процентным приращением индекса, посчитанным по ценам закрытия, — и ее значениями со сдвигом от 1 до 250 шагов назад во времени.

В частности можно видеть, что максимальная взаимная информация считается с переменной с лагом 5, то есть со значением имеющим место одну торговую неделю назад. Также, очевидно, что количество взаимной информации убывает при погружении в лаговое пространство.
Вид функции распределения плотности вероятности для полученного набора значений количества взаимной информации:

Сгенерируем искусственный временной ряд для референсных целей. Источником ряда целых чисел, задающих последовательность значений призна��а был выбран сайт www.random.org. По информации на сайте, они предоставляют действительно случайные числа (в отличие от ГПСЧ, генератора псевдослучайных чисел).
Полученный ряд приращений, со случайно перемешанных хронологическим порядком

На глаз можно отметить насколько более стационарными стали данные.
Этот же ряд с округленными значениями

Гистограмма значений взаимной информации между зависимой переменной и ее значениями со сдвигом от 1 до 250 шагов назад во времени по искусственному временному ряду приращений (с сохранением того же вида функции плотности вероятности на пространстве значений признака)

Вид функции распределения плотности вероятности для данной выборки:

Сравнение 2 рассмотренных случаев расчета взаимной информации

На глаз видно, насколько сильно отличаются полученные выборки значений количества взаимной информации.
Проверим гипотезу о значимости различия (различия вида функции плотности распределения вероятности) двух выборок посчитанных значений взаимной информации — для исходного и искусственного временных рядов. Прибегнув к непараметрическим тестам, посчитаем статистику по методу Колмогорова-Смирнова (тест Колмогорова-Смирнова применяется для сравнения двух независимых выборок значений с целью определить статистическую значимость различий между значениями выборок. Для этой же цели используется U-тест Манна и Уитни).
Результат: p = 0.00 при принятом пороговом уровне значимости 0,05.
Результат U-теста по методу Манна и Уитни: p = 0.00.
Видим, что в обоих случаях гипотеза о различии между выборками значений признака принимается (p меньше 0,05).
Можно сделать вывод о том, что в естественных финансовых данных (по крайней мере, у индекса DJI) есть статистически значимые зависимости произвольного вида между приращениями котировок. То есть, такой ряд данных нельзя считать случайным. Теоретически, существует пространство возможностей прогнозирования будущих значений такого ряда, например, с помощью нейронных сетей.
P.S.: Буду рад комментариям, критике.
В качестве подопытного источника данных возьмем данные DJI за 30 лет (дневные цены закрытия), с 1981-08-31 по 2011-08-26 (Источник: finance.yahoo.com).
Значения индекса Dow Jones Industrial Average (DJI)

Ряд процентных приращений котировок, расчитанный по формуле X[t] / X[t-1] — 1

Для приведения исследуемой непрерывной, по ее сути, переменной к дискретному типу перейдем к ряду процентных приращений, округленных до 0,01 (1%). Подсчет взаимной информации для непрерывных переменных, хотя и возможен технически, но не информативен, в силу очень большого значения n — конечного набора значений признака, принимаемого случайной переменной.

Базовые концепции информационно-теоретических идей, использованных в статье
(Все формулы а также теория заимствованы в: ru.wikipedia.org а также из ряда монографий, которые можно поискать по ключевым словам.)
Теория информация развивалась неразрывно с теорией связи, я не буду отходить от этой традиции.
Что такое информация?
Представим, что есть некий передатчик и приемник данных. Передатчик передает дискретную переменную X, которая принимает ограниченное количество возможных вариантов значений x (это также называется алфавит). Вероятность реализации каждого конкретного значения отличается от нуля, иначе такое значение просто исключается из анализа. Вид функции плотности вероятности на пространстве значений, принимаемых переменной, может быть произвольным. Сумма всех вероятностей по каждому возможному значению равна 1 (если сумма равна 0, то дальнейший ход мыслей не имеет смысла).
Приемник воспринимает передаваемые значения X, или можно сказать, что в точке приема значений осуществляется событие — переменная X приняла значени�� x. И чем меньше мы, то есть, наблюдатели, знаем о том, какое именно событие произойдет (сиречь, какое именно значение примет приемник), тем большей энтропией обладает данная система, и, тем больше информации принесет с собой осуществление этого события.
Значит, информационная энтропия (понятия, заимствованное из энтропии в теоретической физики) это количественная мера неопределенности в абстрактной системе состоящей из возможности реализации события и его непосредственной реализации. Мда, звучит, действительно, абстрактно. Но в этом и сила этой теории: она может применяться к широчайшему классу явлений.
А все же, что такое информация? Это также количественная мера, характеризующая количество энтропии, или неопределенности, которое ушло из системы при реализации конкретного события. Информация, следовательно, количественно равна энтропии.
Если говорят про весь спектр значений, которые реализуются в системе, то говорят про среднюю информацию или информационную энтропию. Эта величина считается по формуле:

Если говорят про информацию отдельно взятой реализации случайной величины, говорят про собственную информацию:

Например, опыт с многократным подкидыванием честной монетки — это система со средней информацией равной 1 Бит (при подстановке в формулу логарифма по основанию 2). При этом, перед каждым подбрасыванием мы ожидаем выпадение решки или орла с равной вероятностью (эти события! независимы! друг от друга) и неопределенность всегда равна 1. А какова будет информационная энтропия этой системы при неравной вероятности выпадения сторон монетки? Скажем, орел выпадает с вероятностью 0,6, а решка — с вероятностью 0,4. Посчитаем и получим: 0,971 Бита. Энтропия системы уменьшилась, так как неопределенность реализации эксперимента уже меньше: мы ожидаем орел чаще, чем решку.
Возвращаясь к примеру с передатчиком и приемником, если связь между ними идеально хорошая, то информация (в широком смысле) будет всегда передаваться на 100% правильно. Иначе говоря, взаимная информация между передатчиком и приемником будет равна средней информации самого приемника (символизирующего реализацию события), а если данные из передатчика будут никак не связаны с данными, получаемым приемником, то взаимная информация между ними будет равна 0. Иначе говоря, то что передает передатчик ничего не говорит о том, что принимает приемник. Если есть некоторые потери информации, то взаимная информация будет величиной от 0 до средней информации приемника.
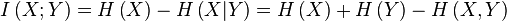
В контексте задачи, о которой я писал в этой статье, взаимная информация выступает инструментом нахождения произвольного вида зависимости между приемником (зависимой переменной) и передатчиком (независимой переменной). Максимизация взаимной информации между парой переменных указывает на наличие некоторой детерминированности реализации случайного значения по отношению к его прошлым реализациям. Можно, конечно, в качестве независимых переменных взять что угодно, от состава поющих птиц по утрам, до частоты определенных слов в интернет-публикациях на тему биржевой торговли. «Истина где-то рядом.»
Итак, посчитаем энтропию источника данных (http://ru.wikipedia.org/):

Средняя информация (или просто энтропия) данного источника данных (посчитанная по логарифму с основанием 2) составляет 2.098 Бит.
Взаимная информация между случайными переменными посчитана через понятие информационной энтропии (http://ru.wikipedia.org/):
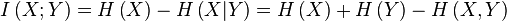
Гистограмма значений взаимной информации между зависимой переменной — процентным приращением индекса, посчитанным по ценам закрытия, — и ее значениями со сдвигом от 1 до 250 шагов назад во времени.

В частности можно видеть, что максимальная взаимная информация считается с переменной с лагом 5, то есть со значением имеющим место одну торговую неделю назад. Также, очевидно, что количество взаимной информации убывает при погружении в лаговое пространство.
Вид функции распределения плотности вероятности для полученного набора значений количества взаимной информации:

Сгенерируем искусственный временной ряд для референсных целей. Источником ряда целых чисел, задающих последовательность значений призна��а был выбран сайт www.random.org. По информации на сайте, они предоставляют действительно случайные числа (в отличие от ГПСЧ, генератора псевдослучайных чисел).
Полученный ряд приращений, со случайно перемешанных хронологическим порядком

На глаз можно отметить насколько более стационарными стали данные.
Этот же ряд с округленными значениями

Гистограмма значений взаимной информации между зависимой переменной и ее значениями со сдвигом от 1 до 250 шагов назад во времени по искусственному временному ряду приращений (с сохранением того же вида функции плотности вероятности на пространстве значений признака)

Вид функции распределения плотности вероятности для данной выборки:

Сравнение 2 рассмотренных случаев расчета взаимной информации

На глаз видно, насколько сильно отличаются полученные выборки значений количества взаимной информации.
Проверим гипотезу о значимости различия (различия вида функции плотности распределения вероятности) двух выборок посчитанных значений взаимной информации — для исходного и искусственного временных рядов. Прибегнув к непараметрическим тестам, посчитаем статистику по методу Колмогорова-Смирнова (тест Колмогорова-Смирнова применяется для сравнения двух независимых выборок значений с целью определить статистическую значимость различий между значениями выборок. Для этой же цели используется U-тест Манна и Уитни).
Результат: p = 0.00 при принятом пороговом уровне значимости 0,05.
Результат U-теста по методу Манна и Уитни: p = 0.00.
Видим, что в обоих случаях гипотеза о различии между выборками значений признака принимается (p меньше 0,05).
Можно сделать вывод о том, что в естественных финансовых данных (по крайней мере, у индекса DJI) есть статистически значимые зависимости произвольного вида между приращениями котировок. То есть, такой ряд данных нельзя считать случайным. Теоретически, существует пространство возможностей прогнозирования будущих значений такого ряда, например, с помощью нейронных сетей.
P.S.: Буду рад комментариям, критике.