Введение
Коллега Bo_bda рассказывает о фундаментальных проблемах обработки и анализа изображений. Что же, не могу остаться стороне и не поделиться своими опытом. Сегодня я вам расскажу о такой занимательной штуке, как марковские сети (markov random fields в зарубежной литературе). Данная математическая модель используется при решении практически всех задач обработки графики (тут вам и сегментация, и восстановление изображений, построение стереоизображений, различные вопросы в 3D и много чего еще). Внимание! Под катом тонны картинок (в блоге о графике-то, к чему бы это).
Постановка задачи
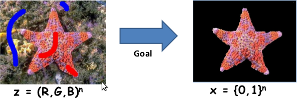Как правило, выделяют 2 вида задач: прямые и обратные. Например, в компьютерной графике часто решается прямая задача: на вход подаем набор источников света, параметры среды, на выходе получаем модель сцены. В компьютерном зрении все с точностью, да наоборот — скармливаем набор изображений, чтобы узнать, где на них интересующая нас вещь (в машинном обучение фигурирует понятие с очень похожим смыслом — регрессия). Более формально задачу можно определить так — для заданного набора значений необходимо вычислить параметры некоторой неизвестной нам модели.Для конкретики попробуем решить следующую задачу: целиком выделим морскую звезду на картинке выше, при условии, что мы можем пометить нужный нам объект (красные мазки) и все остальное (соответственно, синие).
Теоретическая справка
Итак, мазками мы отметили произвольное множество точек, которое удовлетворяет некоторому условию.
Статистическим выводом называется получение информации обо всей выборке на основе ее части (wiki). Существует 2 основных подхода — частотный и байесовский. Воспользуемся последним, так как он оперируется весьма интересным и полезным нам понятием — априорной вероятностью.
Априорное распределение вероятности некоторой величины p — распределение вероятности, которое выражает предположения о p до учёта экспериментальных данных (wiki). Не находите, что очень подходит к нашим условиям? :)
Функция правдоподобия (likelihood) в математической статистике — это совместное распределение выборки из параметрического распределения, рассматриваемое как функция параметра (wiki).
Оценка апостериорного максимума (maximum a posteriori — MAP) позволяет вычислить некую величину с использованием априорного распределения вероятности (wiki).
Ближе к делу
Искомое нами преобразование можно описать следующим образом:
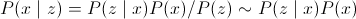, гдеP(x|z) — апостериорная вероятность (wiki);
P(z|x) — функция правдоподобия (зависит от данных, т.е. текущего изображения);
P(x) — априорная вероятность (не зависит от данных).
Фактически, проблему поиска лучшего разделения можно сформулировать таким образом:
(это формула и выражает MAP), или, что тоже самое
, гдеE(x) — энергия изображения.
Рассмотрим каждую часть отдельно.
Функция правдоподобия
Данная функция при x = 0 или x = 1 показывает, относится ли текущий пиксель z к нужной нам области изображения. На рисунке справа можно это увидеть.         Для улучшения результата нам необходимо найти максимум:
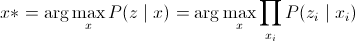
        В результате должно получиться следующее:
Априорная вероятность
Этот параметр позволяет учитывать и соседние пиксели при сегментации. Соединим текущий пиксель с его соседями по вертикали и горизонтали. Тогда:
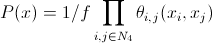, где
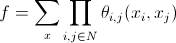— функция разделения;
— «Ising prior» (априорная вероятность Изинга, по подсказке yuriv).При этом всем
Апостериорная вероятность
При определении данного слагаемого воспользуемся распределением Гиббса (wiki):
, где
— энергия изображения, где первое слагаемое — значение энергии текущего пикселя самого по себе, а второе — суммарное значение с соседом; w — некий вес, значение которого определяется экспериментально;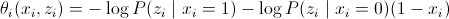
— функция правдоподобия;
— априорная вероятность.Фух, осталось совсем чуть-чуть, самое главное.
Минимизация энергии
Как мы установили в самом начале, минимум энергии соответствует MAP. В этом случае:
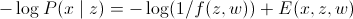
(искомый минимум энергии)Результаты
«Что это было и, главное, ЗАЧЕМ?!», спросит читатель. Вот что в итоге может получиться, с указанием разных значений веса w:
Выводы
Особая прелесть данного метода заключается в том, что формулы энергии мы можем задавать любые. Например, можно добиться выделения на изображении исключительно прямых линий, точек пересечения определенного числа прямых/кривых и многое другое. Кстати, любой счастливый обладатель MS Office 2010 может пощупать описанную технологию. Достаточно использовать инструмент Background Removal.
        Спасибо за внимание!
Уголок копирайтера
Все использованные изображения взяты из работ Carsten Rother. Формулы построены при помощи онлайн интерпретатора Latex.
Список серьезной литературы
- Работы Carsten Rother
- Книга Richard Szeliski «Computer Vision: Algorithms and Applications»