Предисловие и постановка задачи
Думаю, многие читатели этого сайта слышали о такой полезной структуре, как дерево отрезков. А если нет, то о нем в интернете можно отыскать множество интересного материала (здесь, статьи на Хабре: раз и два, google, наконец).
Здесь я разберу обобщение дерева отрезков на двумерный случай, причем (в отличие от этой статьи) рассмотрю реализацию дерева именно с поддержкой групповой модификации элементов.
Вообще, во многих случаях можно обойтись без дерева отрезков вообще, например воспользоваться деревом Фенвика — пишется гораздо легче дерева отрезков, имеет меньшую константу, очевидно распространяется на большие размерности. Но имеет как минимум два минуса: реализует лишь обратимые операции (чтобы заставить его считать минимум/максимум придется изрядно извратится, причем даже тогда оно не будет давать полной свободы действия (в модификации с максимумом — только увеличивать значение, не уменьшать, с минимумом — наоборот)) и не поддерживает групповую модификацию элементов.
Хорошая SQRT-декомпозици с хитрым подбором длины блока также иногда поможет, но все же с мощью дерева отрезков не сравнить.
Итак, задача.
Есть поле NxM, необходимо выполнять два типа запросов:
- Изменить значения ячеек с координатами, удовлетворяющими условиям x1<=x<=x2, y1<=y<=y2 на val
- Вычислить значение некой функции (ассоциативной бинарной операции) от ячеек с координатами, удовлетворяющими условиям x1<=x<=x2, y1<=y<=y2
Здесь я опишу реализацию решения задачи, где функция — сумма. Сразу скажу, что до этого решения я доходил сам (в течении около 15 часов), так что не исключаю существования более простого, и даже рад буду его послушать.
Структура дерева
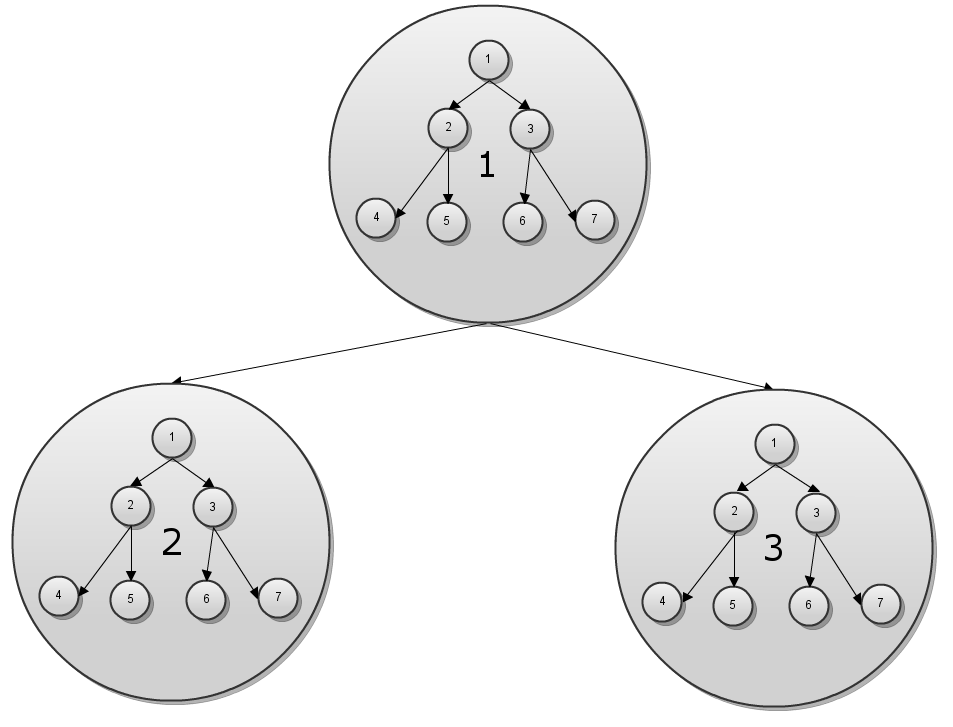
По структуре двумерное дерево отрезков представляет дерево отрезков из деревьев отрезков (в каждом узле дерева глубины X_DEPTH есть «вложенное» дерево глубины Y_DEPTH). Здесь и далее глубина дерева — двоичный логарифм от количества элементов, которое оно может вместить. Например, на рисунке изображено дерево глубины 1, в каждом узле которого содержится дерево глубины 2. Такое дерево может обрабатывать запросы вида [x1;x2]⊆[0;1], [y1;y2]⊆[0;3].
Занумеруем вершины этих деревьев (как внешнего, так и всех вложенных) как обычные одномерные деревья.
Тогда каждая вершина вложенного будет характеризоваться координатой [x][y], x — номер вершины внешнего дерева, в котором она находится, y — внутреннего.
Назовем сектором некоторый прямоугольник, образуемый ячейками x1<=x<=x2, y1<=y<=y2. Тогда каждая вершина вложенного поддерева отвечает за некий сектор.
В каждом узле «вложенного» дерева мы будем хранить четыре параметра:
- add — величина, на которую нужно увеличить результат при запросе суммы на вложенных секторах (потомках по x-й и y-й координатам)
- add_x — величина, на которую нужно увеличить результат при запр��се суммы на не полностью вложенных отрезках (потомках по y-й координате, но с той же x-й)
- add_y — величина, на которую нужно увеличить результат при запросе суммы на не полностью вложенных отрезках (потомках по x-й координате, но с той же y-й)
- value — сумма в поддереве вершины (не считая перечисленных выше добавлений)
В памяти компьютера, как нетрудно понять, эта информация будет представлена четырьмя двумерными массивами.
Препроцессинг операций
Когда мы выполняем операцию модификации, как и в одномерном случае, мы будем изменять значения лишь определенного для данного сектора списка вершин. При суммировании на том же секторе мы будем обращаться к тем же вершинам.
Если мы изменим значение вершины [x0][y0], отвечающую за сектор [x0_1;x0_2][y0_1;y0_2], то не трудно понять, что все сектора, включающие этот сектор могут быть найдены как пары (x;y): x1<=x0_1 AND x0_2<=x2 AND y1<=y0_1 AND y0_2<=y2. т. е. Достаточно собрать множество X x-овых, Y для y-овых, а потом перебрать все пары из XxY.
Ну а чтобы собрать эти самые списки, необходимо пройти по вершинам, как в случае с запросом на одномерно дереве.
Рассматривая же конкретную пару (x;y) можно легко вычислить xl, xr, yl, yr — границы секотра текущей вершины, а также xc и yc — количества элементов в пересечениях по x-овой и y-овой осях.
Операция модификации
- Если запрос полностью включает в себя сектор текущей вершины, то нужно добавить в add вершины изменение val (ко всем потомкам и по x-й и по y-й нужно прибавить val):
add +=val;
- Если запрос включает текущий сектор лишь по x-й кординате, изменяем add_y:
add_y += val*xc;
- Если запрос включает текущий сектор лишь по y-й кординате, изменяем add_x:
add_x += val*yc;
- Если запрос не включает сектор вообще:
value += val*xc*yc;
С add, думаю, все понятно (см одномерный случай).
Когда запрос включает текущий сектор по y-й координате, значит по y-й могут быть потомки, которые не будут затронуты в данном запросе, но будут при запросах суммы в дальнейшем. Потому мы и увеличиваем add_x.
Аналогично и с add_y.
И, наконец, если ни одно из трех предыдущих условий не соблюдено, значит сред прямых потомков данной вершины один изменится, а второй нет. Следовательно, данное изменение нужно учесть, но не распространять дальше. Увеличиваем value.
Операция суммирования
Обозначим за res результат запроса, который мы и будем вычислять. Дополнительно к препроцессингу, вычислим границы той части запроса, которую мы ищем в данной вершине (границы искомой части):
xvl = max(xl, x1), xvr = min(xr, x2), yvl = max(yl, y1), yvr = min(yr, y2)
- Нам необходимо прибавить ко всем ячейкам запроса, лежащих в текущем секторе add текущей вершины:
res += add*xc*yc;
- Если искомая часть равна сектору вершины по x-овому диапозону:
res += add_x*yc;
- Если искомая часть равна сектору вершины по y-овому диапозону:
res += add_y*xc;
- Если сектор текущей вершины целиком лежит в запросе (ниже мы спускаться не будем):
res += value;
Асимптотика
Как видно из описания, данное решение будет работать за O(N*X_DEPTH*Y_DEPTH), где N — количество запросов.
Реализация
Реализацию этого решения можете посмотреть по ссылке http://dl.dropbox.com/u/3693476/articles/segtree2d/segtree2d.cpp (файл-решение задачи Ферма, D из файла http://dl.dropbox.com/u/3693476/articles/segtree2d/problems01.pdf). Если хотите получить тесты к этой задаче, чтобы отладить своё решение, напишите свою просьбу на мой почтовый ящик george.agapov@gmail.com.
P.S. Спасибо всем за внимание, надеюсь эта статья будет кому-нибудь полезна.